地下水位升降过程中的黏土地基孔压变化试验研究

唐逸凡,焦艳梅,刘新原,齐大洪,宋林辉

(1. 南京工业大学 数理科学学院,江苏 南京 211800;2. 徐州地铁集团有限公司,江苏 徐州 221000)

城市地下工程近年来得到大规模的发展,地下结构抗浮是工程设计中的一个重要课题,尤其是在频发的极端暴雨条件下,突增水位对已建地下结构的抗浮带来严峻挑战[1]。浮力大小主要取决于基底孔压,已有模型试验显示,砂土层中的基底孔压等于理论水压强,其浮力可按阿基米德理论公式计算[2],而黏土层中的基底孔压则比较难确定,争议较大[3-4],研究表明:其相比理论水压强,存在明显的折减和滞后[5-6]。实际上,砂土层和黏土层中孔压的差异主要体现在对孔压的传递上[7],砂土中的孔压与水压类似,可瞬间声速传递,而黏土方面,倪春海等[8]在黏土层顶部,陆启贤等[9]在黏土层侧面施加水压探讨孔压传递规律,均发现黏土中的孔压传递比较慢。另外,有学者专门研究了外界条件变化下的孔压响应,Abdollahi等[10]基于渗流-变形耦合模型对海啸荷载下的地基土进行数值模拟,发现土体中的孔压受海啸高度和持续时间的综合影响。Wang等[11]对未扰动软黏土进行主应力轴旋转试验,发现孔压积累随主应力的旋转而波动。Di Miao等[12]通过对斜坡孔压监测发现,降雨是造成边坡深层孔隙水压力变化的主要因素之一。Wang等[13]在非均质边坡稳定性研究中也发现孔压会随着降雨强度的增大而上涨,从而导致边坡稳定性降低。Huang等[14]发现,结构化土体中孔压的变化对于施加的应力大小更为敏感。Wang等[15]在分析三峡水库舒坪滑坡事件时发现,滑坡体内部孔压和水库水位的波动一致,但具有明显的滞后性。应宏伟等[16-17]推导半解析解,分析地下水位波动下基坑周围地基土的孔压响应及对挡墙稳定性的影响。Jin等[18]采用离心模型试验,研究了土石坝中的孔压和位移在水位波动下的特性。上述文献关注的主要是土体超静孔压的消散过程,孔压的变化还受土层的渗流和渗透系数的影响[19],章丽莎[20]分析地下水位变化对地基及基坑渗流特性的影响。宋林辉等[21]通过试验发现:在自上而下的水压作用下,土体的渗透系数会减小,并引起孔压消散滞后时间延长。综上所述,现有研究主要是关注静止水位下的基底孔压大小和水位变化下的超静孔压消散问题,水位变化后的孔压传递过程和基底孔压变化有待研究。

1 试验方案

1.1 试验思路

针对季节性丰枯水期和暴雨导致的地下水位升降条件下地下结构基底黏土层中的孔压变化规律,开展试验研究,研究思路如图1所示。由图1可知:选取地下水位下一定深度处的分析单元,先施加固结压力和水压以恢复其现场自重应力状态,再变化水压大小以模拟水位上升、回落和下降,同时监测黏土层中不同位置处的孔压,从而得出孔压变化规律。

图1 研究思路Fig.1 Conceptual framework

1.2 试验工况

参照不同深度土体所处应力状态,设置3组固结压力和初始水压(分别模拟地下10、20、30 m处土体的应力),制定试验加载方案(表1)。

表1 试验加载方案

由表1可知:一共进行3组试验(T1、T2、T3),每组试验在初始水压G0基础上按20%的幅度增减水压大小,以模拟水位上升、回落、下降3种工况(G1、G2、G3)。

1.3 试验土体

试验用土取自某基坑坑底,勘察报告显示,土体为黄色黏土,将其运至实验室,晾干、粉碎、过1 mm 筛后,进行液塑限指标试验,得到的物理参数如表2所示。由表2可知:试验土体为低液限黏土。

表2 土体物理参数

1.4 试验设备

依据试验要求,研制了一套刚性壁固结渗透装置,包括渗透测试筒、固结压力施加杠杆、水压施加设备和数据采集系统,其中的渗透测试筒是关键部件(图2)。由图2可知:渗透测试筒由钢底座、有机玻璃渗流筒和钢盖板组成,三者相互之间采用橡胶垫和螺栓连接,可装配形成密闭腔体。钢底座侧边留有带测压孔的进水孔A,以便从底部施加确定的水压。筒体总高60 cm、内径20 cm,筒体侧壁沿高度方向每隔10 cm均匀设置了5个测压孔(孔内设有透水石),测压孔通过细管与孔压传感器相连,并利用电脑自动采集数据。钢盖板中间设有加压杆套,加压杆通过杆套穿过盖板传递杠杆荷载给试样施加固结压力,加压杆上加装了位移测试板,用于放置位移计;盖板上另设2个孔道,一个是带水压表的排泄孔,用来排气排水,另一个是进水孔B,用于试验前的注水;2个进水孔和1个排泄孔均设有阀门,可按需开启和关闭。

图2 渗透测试筒(cm)Fig.2 Container of penetration test (cm)

水压是由气泵经密闭罐施加的,密闭罐是带气囊的,将内部空间分成气室和水室,其中气室的进气口接气泵,水室的出水口接渗流筒钢底座上的进水孔A,气泵加压后,气室的压力传递到水室实现加压,且可避免气体混入水中。

孔压计采用的是杭州美控自动化技术有限公司生产的进口扩散硅水压传感器,量程0～0.6 MPa、综合精度0.25级。试验前,通过将渗透测试筒(图2)注满水后打倒平放,按50 kPa增幅逐级施加水压至500 kPa,一次性对6个孔压计进行标定,并依据标定线挑选孔压计,最后安装使用的孔压计标定数据线性良好,精度在0.5 kPa以内。另外,筒顶备用的水压表采用的是上海自动化仪表四厂生产的YB-150A型精密压力表,量程0～1.0 MPa、精度0.40级。

1.5 试验步骤

参照试验工况,每组试验可分为7个步骤。

① 准备工作:组装试验装置并进行密封性检测,确保试验过程中不漏水;同时,将粉碎过筛后的黏土放入饱和桶中抽气饱和,时间不少于24 h。

② 防渗漏处理:在渗流测试筒内壁涂抹一层凡士林,其中接孔压计的孔口处及往上5 cm区域在抹凡士林前贴上1 cm宽的纸胶带,抹好凡士林后再撕掉,这样既可避免筒壁与土体界面间的渗漏,又能避免凡士林堵住孔口。

③ 土体填筑:将饱和好的黏土分层填入渗流筒内,并打开侧壁的测压孔和底座的进水孔A,静置10 h以上,以使土体在自重下排水固结。为保证土样的均质性,除了前述过1 mm筛网和抽气饱和24 h以上外,还通过使用透明筒体直接观察分层填入土体的状态,并在完成填土后,将渗流测试筒置于高频底幅振动台上振动约5 min,振后土体呈黏糊状。

④ 加压固结:将筒内上层的浮浆移除,填入厚约5 cm用于找平的砂层,通过杠杆逐级施加荷载直至达到表1中每组试验所要求的固结压力,且在该固结压力下土体的沉降稳定,即变形小于0.01 mm/h。

⑤ 施加水压:用注满水的高压水管将筒壁测压孔与孔压传感器连接,进水孔B与水桶连接,然后从排泄孔中抽气,水在负压下流入筒上部,保证无气泡,注满后关闭排泄孔和进水孔B。再由进水孔A从试样底部施加初始水压,静置2 d以上,以形成土体所处的自重应力状态,装置照片如图3所示。

图3 试验装置照片Fig.3 Photo of experimental setup

⑥ 变化水压:开启数据采集系统,采集每组试验中各测点的初始孔压,并设置数据采集间隔为0.05 h;然后按表1增减水压,以模拟水位上升、回落、下降3种工况,每种工况下,各测点孔压均需达到稳定状态,稳定状态的判断标准是每小时的孔压变化小于该组试验初始水压(pw0)的0.3%,每组试验的时间不少于48 h。试验结束后,将对试样取样进行常规土工试验,表3为每组试样的物理参数。

表3 每组试样的物理参数

⑦ 数据处理与分析:运用采集的数据对比各测点的孔压和变化规律,并与理论值对比。

2 孔压测试结果

依据试验步骤①—⑤,可完成3种应力状态试样的制作,并得到初始孔压;再依据试验步骤⑥,分别增大和减小3组试样上所施加的水压大小,可得到水位上升、回落和下降3种工况下土层中的孔压变化情况,现按工况逐个讨论。

2.1 理论孔压与初始孔压

前述不同固结压力和水压下的组合共形成9种试验工况,为便于后期的对比分析,现将9种试验工况下各测点在静水压状态下的理论孔压列于表4中。

表4 不同试验工况下的理论孔压

施加固结压力和初始水压并沉降稳定后,3个试样各点的初始孔压如表5所示。

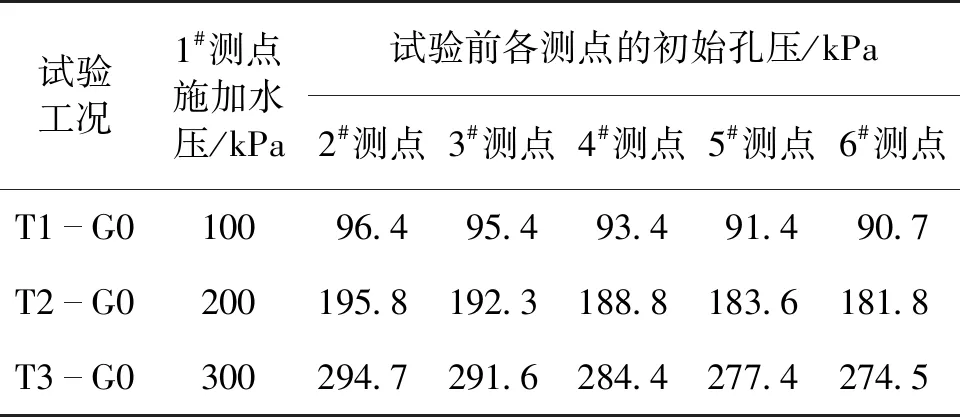
表5 初始孔压

2.2 水位上升时的孔压变化

先对3组试样施加增量水压以模拟G1水位上升工况,该工况下各测点的孔压变化如图4所示。由图4可见:1#测点的水压瞬间增大到设定大小,试验过程中有因补充压力而出现的微小波动;位于试样中的2#～5#这4个测点的孔压变化响应是从2#测点逐个传递至5#测点的,2#测点距离1#测点最近,5#测点距离1#测点最远,表明增加的孔压在黏土中传递需要时间,存在滞后效应。6#测点基本与5#测点变化同步,因为6#测点位于水中,说明孔压在水中的传递很快,无滞后。

图4 水位上升时(G1)各测点孔压随时间的变化Fig.4 Variation of pore pressure with time at each measuring point under rising water level (G1)

孔压的变化都经历了由陡增到缓增的过程,不同试样的孔压在15 h内都将达到稳定状态,且可得到各点的上升稳定孔压。另外,不同试样孔压进入稳定状态的时长随固结压力的增大而增大,因为固结压力越大,土体越密实,渗透系数越小,达到渗流稳定所需的时间就越长。为直观对比,将上升稳定孔压和试验结束孔压除以表4中对应试验工况的理论孔压,可得孔压比,并沿测点位置高度绘制成图5。由图5可见:试样中下部的孔压比在0.98以上,与理论值很接近,试样上部的最小孔压比约为0.92。孔压比实际是孔压的折减系数,即水位上升过程中,稳定孔压达到了理论值的92%以上,在后续30多个小时中,各点孔压缓慢增大,但增量很小,最小孔压比增至0.95左右,即孔压的折减量在5%以内。

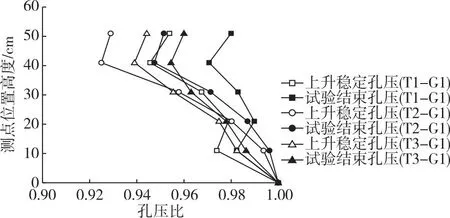
图5 水位上升工况下的孔压比Fig.5 Ratio of pore water pressure under rising water level

2.3 水位回落时的孔压变化

将施加在试样上的增量水压卸除,降至初始水压大小以模拟G2水位回落工况,则该工况下各测点的孔压变化如图6所示。由图6可见:1#测点水压瞬间回落到设定大小,其余各点的孔压变化均经历了由陡降到缓降的过程。对于6#测点的孔压,在T1-G2工况下大于5#测点的孔压、在T2-G2工况下大于4#和5#测点的孔压、在T3-G2工况下大于3#、4#、5#测点的孔压,表明有水压滞留在渗流测试筒上部,且固结压力越大,滞留的压力越大,表明弱透水性土中的渗流存在滞后现象。

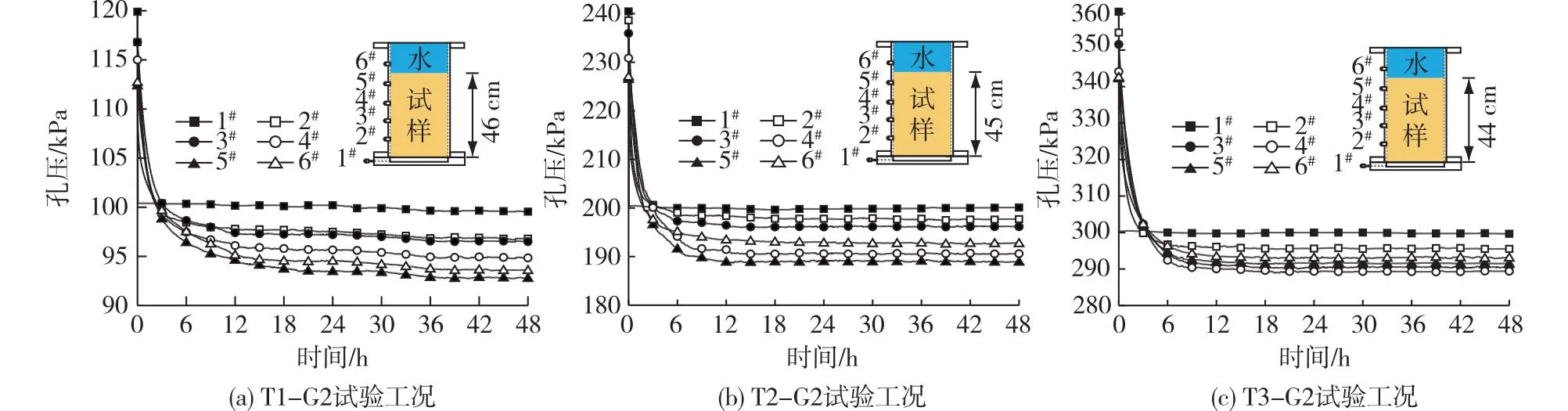
图6 水位回落时(G2)各测点孔压随时间的变化Fig.6 Variation of pore pressure with time at each measuring point under falling water level (G2)

当水位回落时,不同试样的孔压在11 h内都将达到稳定状态,且可得到各点的回落稳定孔压,将回落稳定孔压做与前述相同的处理,可得到水位回落工况下的孔压比(图7)。由图7可见:水位回落过程中的孔压达到稳定时,各点的孔压比在0.98以上,即孔压为理论值的98%,特别是6#测点的孔压还略大于理论值,后续测试时间内孔压比呈减小趋势,最小孔压比降至0.96左右,即孔压的折减量在4%以内,其大小与G1工况很接近。

图7 水位回落工况下的孔压比Fig.7 Ratio of pore water pressure under falling water level

值得强调的是,G1工况的孔压折减量随时间的延长而减小,到试验结束时减至5%;而G2工况的孔压折减量随时间的延长而增大,到试验结束时增至4%。两者的变化趋势刚好相反,假若试验时间无限长,两者将达到一个相同值,在此可取平均值4.5%。

2.4 水位下降时的孔压变化

继续将施加在试样上的水压降低0.2pw0,以进行水位下降工况(G3)试验,则该工况下各测点的孔压变化如图8所示。由图8可见:孔压整体变化趋势与水位回落相同,但水位下降时,孔压达到稳定状态的时间比水位回落时稍长,这是因为施加的水压降低,水力梯度减小,相同渗流量的渗流时间延长。

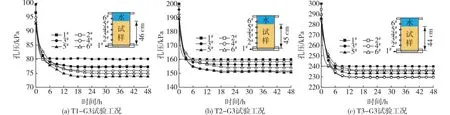
图8 水位下降时(G3)各测点孔压随时间的变化Fig.8 Variation of pore pressure with time at each measuring point under declining water level (G3)

水位下降时,不同试样的孔压在15 h内都将达到稳定状态,且可得到各点的下降稳定孔压,将下降稳定孔压做与前述相同的处理,可得到水位下降工况下的孔压比(图9)。由图9可见:水位下降过程中,各点孔压在达到稳定时的大小非常接近理论值,孔压比在0.97以上,即孔压为理论值的97%,且6#测点的水压因滞留在筒上部,超出静水压理论值。在后续过程中,各点孔压仅有微小减幅,最终的孔压比在0.96以上,即孔压折减量在4%以内,与G2工况相同。

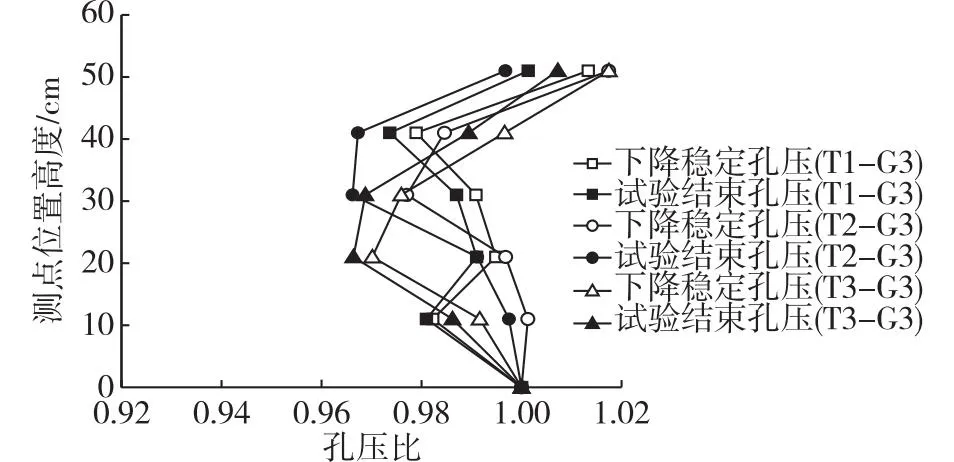
图9 水位下降工况下的孔压比Fig.9 Ratio of pore water pressure under declining water level

3 孔压变化影响因素分析

上述测试数据表明不管是水位上升、回落还是下降,土体内的孔压变化响应都较快,且48 h后与理论值相差4%～5%。孔压变化是渗流和水压传递的表现,主要受施加在土体上的固结压力和水压的影响,其中固结压力是压密土体、减小渗流通道、减缓孔压变化响应的,而水压是提高水力梯度、增大渗流驱动力、加快孔压变化响应的,前述不同工况下的孔压变化响应是两者综合作用下的表现。

另外,水压施加历史亦对孔压变化响应有较大影响,比如G0初始工况和G2水位回落工况下的固结压力和施加的水压完全相同。图10为按前述方法处理得到的G0和G2工况下的孔压比。由图10可见:水位回落后,各测点的孔压比更趋向1,即更接近理论值,原因是试样之前经历了水位上升工况,施加过较大水压,打开了更多的渗流通道,增量水压卸除后,部分流道依旧保持流通状态,使得渗流更充分、孔压变化响应更快速。

图10 G2和G0工况下的孔压比Fig.10 Ratio of pore water pressure in the cases of G2 and G0

变化水压会在试样中形成水头差和水力梯度,从而驱动渗流,现具体分析水力梯度对孔压变化的影响,示意图如图11所示。

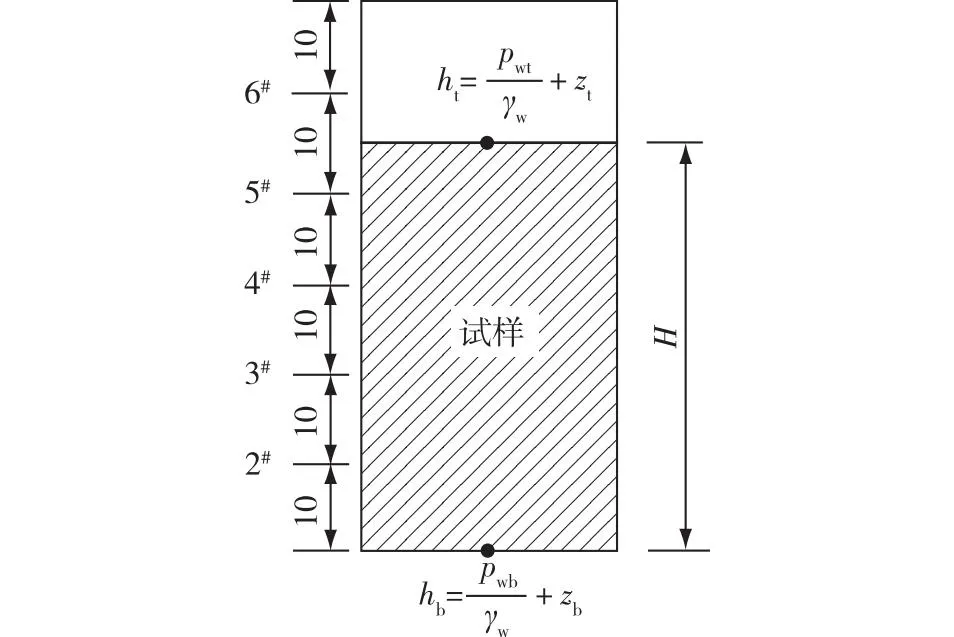
图11 作用在试样上的水头示意图(cm) Fig.11 Schematic diagram of water head acting on the sample (cm)

由图11可知:在G1水位上升工况下,试样底部的总水头(hb)高于顶部的总水头(ht),形成向上的渗流,其水力梯度(i1)为

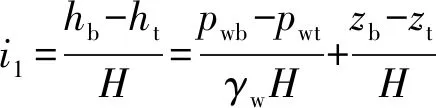
(1)

式中:pwb和pwt分别为试样底部和顶部水压,zb和zt分别为试样底部和顶部位置水头,γw为水的重度,H为试样的高度。

在G2水位回落和G3水位下降工况下,试样底部的总水头(hb)低于顶部的总水头(ht),形成向下的渗流,其水力梯度(i2)为

(2)

基于上述测试数据,利用式(1)和(2),可计算得到3组试验(T1、T2和T3)在3种工况(G1、G2和G3)下,初始时刻和孔压稳定时刻时的水力梯度,如表6所示。

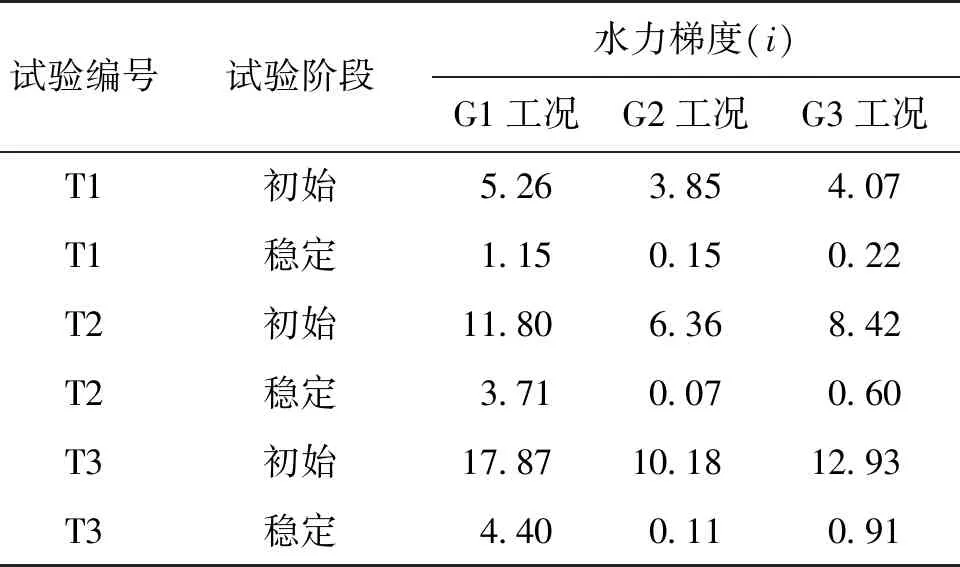
表6 水力梯度

由表6可知:在G1水位上升工况下,3个试样达到孔压稳定时的水力梯度为1.15～4.40,固结压力越大,所需水力梯度也越大;在G2水位回落和G3水位下降工况下,水位下降比水位回落所需水力梯度稍大,两者达到孔压稳定时所需水力梯度为0.07～0.91,整体较水位上升工况要小,两者相差一个数量级。因此,水位上升对孔压形成影响的条件相对较高,水位下降的条件相对较低,水位回落的条件最低,孔压变化响应最快。

与实际工程相比,试验中的6#测点水压即是浮力计算中的水压强,现整理出6#测点水压每隔1 h的数据,并计算得到水压变化率,结果如图12所示。

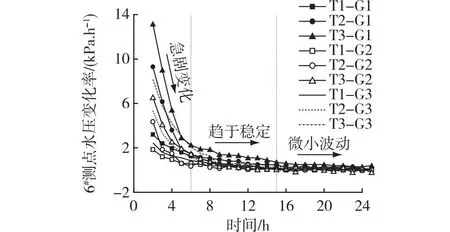
图12 试样顶部的水压变化率Fig.12 Change rate of water pressure at the top of sample

由图12可见:虽然每个试验工况的时间均为48 h,考虑到前2 h的水压变化率过大,后24 h的水压变化率基本不变,故取2～24 h期间的典型阶段进行分析,从水压变化率曲线可见,前6 h水压处于急剧变化阶段,6～15 h水压逐步趋于稳定,15 h以后水压便进入微小波动阶段。因此,据试验结果可知:水位升降在基底引起的水压变化响应较快,并在15 h内达到稳定状态,且水压稳定时的水力梯度范围为0.07～4.40。而在实际工程中,由于渗流路径长,水位升降产生的水力梯度往往很小,围护结构的坑底深度和基坑挖深(D)按1∶1考虑,则坑外水位到基底的渗流路径(L)长约3D,前述20%幅度的升降水位形成的水力梯度约为0.067,与水力梯度试验值相比,该值在孔压处于稳定状态的水力梯度范围内,即不会在土体中形成渗流或引起的渗流流速极慢,短期内对基底水压基本没有影响。

4 结论

针对暴雨条件下黏土中的地下结构是否会浮起的工程问题,笔者着眼于黏土地基中的基底孔压,开展不同应力条件下的黏土渗流试验,重点研究了水位上升、回落和下降过程中土层内孔压的变化规律,分析了水力梯度对孔压变化的影响,得到如下结论:

1)黏土地基中的孔压相比理论值存在少量的折减,在水位上升工况下,各点孔压均随时间的延长而增大,上升稳定孔压为理论值的92%以上,之后继续微增至95%左右,折减量约为5%;在水位回落和下降工况下,各点孔压均随时间减小,稳定孔压超过理论值的97%,之后继续微降至96%左右,折减量约为4%。

2)影响孔压变化的因素包括固结压力、水压及其施加历史、水力梯度。固结压力越大,土体越密实,孔压变化越滞后;水压具有增加流道的作用,施加过水压,水压越大,则孔压变化越快;只有产生足够大的水力梯度才能引起孔压变化,水位上升工况下的水力梯度为1.15～4.40时,孔压处于稳定状态,水位回落和下降工况下的水力梯度为0.07～0.91,且土体越密实,孔压稳定时的水力梯度越大。

3)在实际工程中,20%幅度的升降水位形成的水力梯度约为0.067,未达到引起孔压变化的下限值,故其在土体中形成的渗流流速极慢,短期内对基底水压基本没有影响。

上述结论适用于黏土地基及位于其中的地下结构,对于砂土地基或肥槽回填不当的地下结构,地下水位升降会引起基底孔压的实时响应,危及地下结构的安全,本文研究结果为此类问题的处理提供了方向和理论依据,具有很好的工程价值。