数理统计与分析在卷烟过程质量检验中的应用

刘文杰

（贵州中烟工业有限责任公司毕节卷烟厂，贵州 毕节 551700）

数理统计学，是一项科学的统计方法，用来解决各项实际问题。能够通过对各项数据的整理排列，来直观的呈现出各项数据中所反应的问题，从而去预防或是制定措施来解决问题。在卷烟生产过程中会产生大量的数据，通过数理统计和分析，可以得到各工序的生产信息，从而对每个工序环节进行有效把控，从而有效提高产品质量。

数理统计起源于古典时期的测地学，发展于近代小样本理论的形成。近代统计知识在“洋务运动”时期随《决疑数学》传入我国，于20 世纪前期缓慢发酵，在新中国成立后得到迅速发展，并在各行业中形成统计与分析结合的改进循环。保证数据有效性方面，张德然找到利用跳跃度来检验异常值的方法，王小凯和朱小文对3 种统计学中判别和剔除异常值的方法进行了研究，以上研究发现拉依达准则更适用于大样本但精准性不高，格布拉斯准则精准性高但用于大样本时计算量较大。以上研究从标准偏差、回归分析、方差分析等角度，对数理统计和分析在实际中的应用进行了阐述。接下来论述的数理统计和分析在卷烟产品质量检测中的应用，借鉴了以上相关论文的研究成果，目的是让检测人员有效进行数据的整理和分析等工作。

对卷烟生产过程质量检验数据进行统计分析的步骤通常如图1。卷烟生产过程质量检验中，会得到大量杂乱的数据，这些数据包含了产品的各项指标，通过数据的整理，去除无用的信息，将有效的信息保留梳理，再进行分析处理，就可以得到产品的质量变化规律，发现问题并制定相应措施来解决问题，依据数据分析而制定的解决问题的方法具有准确性和高效性的优点。

图1 检验数据统计分析步骤

1 数据获取后的整理归纳

比如在卷烟物理指标检验工作中，以卷烟成品中单支克重的检测数据为例，检测者收集的4000 个某牌号卷烟单支克重检验数据，其分布情况见图2，其横坐标单位为g，纵坐标为数据个数。

图2 某牌号卷烟单支克重检测数据的分布图

由图2 可见，烟支重量是具有波动性的，且整体呈正态分布规律进行波动，下面将用这组数据来说明异常值的验证与剔除，平均值、中位数与众数，以及更多统计参数等在实际中的使用。

1.1 异常值验证与剔除的应用

从图2 数据看出，重量小于0.82 g 的数据有93个，不符合正态分布的规律，在整理数据时就必须考虑该组数据中是否存在异常值。分析者通常将一组数据中与平均值有较大差异的数据定义为异常值，因为这些数据可能由于操作失误、仪器故障或其他一些随机因素导致。以国际上较为推荐的格拉布斯检验法为例，格拉布斯检验法以正态分布为前提，将4 000 数据按大小顺序排列并切片为40 组子数据，子数据第一组为（x1，x41，x81...x3961）、第二组为（x2，x42，x82...x3962）依次类推。以第一组数据计算，用最大值 x（max）=0.859 与 最 小 值 x（min）=0.821 分 别 减 去均 值 x（mean）=0.8486， 差 值 最 大 为 |x（min）-x（mean）|=0.0276，将最小值的定义为可疑值x1，i 为可疑值x 的排列序号，数据组的标准偏差x（S.D）=0.005 28，根据公式：Gi=|（xi- x（mean））/x（S.D）|=5.227

格拉布斯表置信概率P 值可以设置0.9～0.995 的范围，值越大要求越严格。根据P 值（此处取0.99）和数据数量（此处为100）查格拉布斯表G99（100）=3.6，Gi＞G99（100），则能判断该测量数据是异常值，可以剔除。剩下的数据再次进行判定直到Gi＜GP（n）为止。图2 中重量93 个小于0.82 g 和6 个0.82～0.822 g 间的单支克重数据就判定为异常值，从而可以发现检测过程或检测仪器出现了问题。格拉布斯检验法对异常值的判定较为精准且得到国际上广泛认可，但其在处理海量数据时计算量过大，这时可以考虑使用精度较差，但计算简单的拉依达准则。其只要满足 |（xi- x（mean））|≥ 3 x（S.D），就能将可疑值xi判定为异常值进行剔除。

1.2 平均值、中位数与众数的应用

平均值在卷烟成品质量的数据统计中通常指算数平均值，是统计学中最基本、最常用的一种平均指标，代表一组数据的平均水平。中位数又称中值，是按顺序排列的一组数据中居于中间位置的数。众数是指在统计分布上具有明显集中趋势点的数值，代表一组数据中出现次数最多的数值。平均值、中位数、众数都表示数据的集中位置。平均值适用范围广，但受异常数据影响较大；中位数具有良好抵抗性，受异常数据影响较小，但不适用于小样本或是分布偏态的数据；众数能更好代表一组数据的分布情况，但其缺点是一组数据可能出现多个众数，使得可靠性较差。如图2，案例中均值0.853 就受到了异常值的影响，使得均值偏大而不能较好的表示数据的集中位置，而众数0.852 与中位数0.851 较为准确地反映了这组数据的集中位置。

1.3 更多统计参数的应用

查看一组数据是否异常可以使用异常值验证，判断一组数据集中趋势可以计算其均值、中位数、众数、四分位数等；衡量一组数据的离散程度可以使用标准偏差、极差、变异系数等。以上都是数据整理归纳常用到的统计参数，但数据的使用不只包含以上内容，还有衡量数据准确性的置信区间、检验统计假设是否正确的显著性检验等，但置信区间及显著性检验较少用到，所以不再详细阐述。在对数据进行整理统计时，需要对数据的使用有合理的判断，即在统计前根据统计研究的目的和研究对象的特点，明确统计指标和指标体系，以及对应的分组方法，这样才能较好的以分析方法指导实际的统计活动。

2 以数理统计的方法来找出影响结果的原因

2.1 回归方程分析的应用

回归分析分为线性回归、逻辑回归、多项式回归、逐步回归等，其是衡量两种因素之间相互关系的统计分析方法。根据因素的多少分为一元回归和多元回归分析，根据因素所影响的其他因素多少分为简单回归和多元回归分析，根据因素和其所影响的因素的关系又分为线性回归和非线性回归分析。

以Minitab 软件进行回归分析为例，在卷烟成品质量检验中，得到烟支重量与烟支吸阻数据如表1。

表1 烟支重量与烟支吸阻数据

设烟支重量为因素X，烟支吸阻为烟支重量这一因素X 所影响的因素Y，通常可以建立线性关系：Y=A+BX+§。公式中A 和B 为待计算出的参数，其中A 表示回归直线的截距，B 表示直线的斜率，§表示随机误差。在Minitab 中对数据进行回归分析得到线性关系为 Y=-590.8+2 033.9X

公式表示每当烟支重量X 提高或降低0.01 g 时，吸阻Y 就会相应提高或降低20.33 Pa，如图3，两者呈正相关关系。

图3 烟支重量与烟支吸阻回归方程及数据散点图

回归分析能够找到两因素之间确定性的函数关系，建立起因素间沟通联系的桥梁，还能对两个因素间相互影响作用做出判定。对烟支重量和吸阻进行回归分析得到结果如表2。

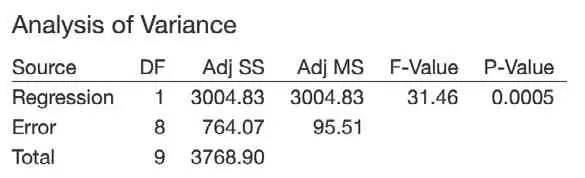
表2 烟支重量与烟支吸阻回归分析结果

Minitab 使用 F-Value 和 P-Value 表示因素间的影相互影响，F-Value 表示用于确定项是否与响应值相关的检验统计量，通常F-Value 越大表明项对响应值影响越显著。P-Value 由F-Value 计算得出，是一个概率值，其用来衡量否定原假设的证据，概率越低，否定原假设的证据越充分。通常，显著性水平α=0.05，当P-Value ＜α 时，可以判断均值之间的差值在统计意义上显著，换言之，表示因素间存在显著的关联性。表2 中P-Value 为0.000 5 ＜α，所以烟支重量的变化对烟支吸阻有显著影响。

2.2 方差分析的应用

方差分析又称变异系数分析，其原理与回归分析一样，不同的是回归分析较适用于连续和线性的模型分析，而方差分析适用于特殊和离散的模型分析，简单来说，方差分析实际上是特殊情况的回归分析。比如研究烟支重量对烟支吸阻的影响，因为重量与吸阻的变化曲线都是线性的，这时用回归分析较为准确，但研究不同种类、不同品牌的卷烟辅料对成品烟支的物理指标影响，不同种类的辅料和不同厂家的辅料其变化是非线性的，这时使用方差分析较为合适。因方差分析与回归分析方法一致，此处不再赘述。

3 计量对数据统计分析的影响

计量是一种实现单位统一、量值准确可靠的活动。在卷烟过程质量检验中，计量工作通过检验、测量和试验仪器的量值校准、传递、调整，来确保量值的准确性和一致性，让检测结果尽可能接近被测量的真值，以及测量结果呈现可再现的属性，换言之，计量是数据统计分析结果准确的基石。如果计量准确性得不到有效保障，数据分析的结果很可能把问题导向错误的方向，进一步导致做出错误的决策对工艺流程进行不恰当的调整和改进，导致新的问题出现或是造成不合格品的产生。而如果计量的一致性得不到有效保障，数据的随机因素增大，很可能使得问题无法被发现或是分析结果偏差过大，导致生产过程的工艺参数调整不准确。在图2 中，对烟支的称重仪器正是因为计量准确性得不到保障，检测数据异常出现93 个重量极端偏小的烟支，而在日常生产中进行的小样本分析时，较少会进行异常值剔除，很难发现这样的计量错误，该错误会使得烟支重量整体均值偏小，导致在对重量进行控制时，进行错误的工艺参数调整。

4 结语

通过上述案例可以知道，面对卷烟生产过程中产生的大量检测数据，应该如何合理选择和应用数理统计和分析手段来发现生产中的问题：（1）异常值的验证和剔除。通过格拉布斯检验法或拉依达准则等对异常值进行验证和剔除，以消除异常值对统计分析结果的影响。（2）平均值、中位数和众数都可以观察数据的集中趋势，但不同情况要合理使用不同的集中位置衡量参数。同样，观察数据离散程度也有标准偏差、极差等不同衡量参数，需要合理利用好这些参数。（3）通过回归方程分析和方差分析等方法建立起因素间联系的桥梁，可以有效对因素间互相影响的程度进行判定，但也需要合理的选择分析方法。（4）计量是保证数据的准确性和一致性，是保证数据统计分析结果准确的基石。随着社会科学技术的发展，现阶段很多统计分析软件都实现了更高的智能化，常见的统计分析软件有Spss、Minitab、Design-Expert、Matlab 等。软件智能化水平的提高降低了进行数据统计分析的门槛，只要能熟练掌握这些智能化统计分析软件，并了解各种参数和分析方法的原理并正确选择，就能够满足卷烟生产过程中质量统计分析的要求。顺应时代发展，相信分析方法的不断完善，统计分析软件的不断更新换代，企业从数据中发现问题的能力不断提高，卷烟制造业的产品质量水平也会不断向好。