基于图神经网络的子图匹配符号算法

杨 欣, 徐周波, 陈浦青, 刘华东

(桂林电子科技大学 计算机与信息安全学院,广西 桂林 541004)

图作为一种数据结构,可以有效刻画事物之间的关系,现实世界中的许多复杂问题都可以用图进行抽象表示。子图匹配问题作为图分析中最基本的问题之一,其目标是在数据图g中查找与查询图q同构的所有子图[1],在图像检索、化学分子式检索、知识图谱查询和社交网络分析等领域有着广泛应用[2]。由于子图匹配问题属于NP难问题,随着数据规模的急剧增加,其求解的复杂度呈指数增长,因此广大研究者致力于扩大子图匹配问题的求解规模和提升求解效率。

在过去几十年,大量子图匹配算法被提出,其中基于回溯搜索的算法[3-13]更是被广泛研究。著名的Ullmann算法[3]于1979年提出,该算法基于回溯的树搜索在数据图g中枚举出与查询图q匹配的所有子图。由于Ullmann算法只采用了简单的剪枝策略,无法高效地减少搜索空间。VF2[4]算法在Ullmann算法的基础上,将节点的邻居信息作为约束条件,增强了剪枝效果,有效地减少了搜索空间。GraphQL算法[5]提出以查询图的深度优先搜索生成树过滤数据图中的节点。Spath算法[6]采用对查询图进行层次遍历并以每层节点的信息作为约束条件,引入复杂的结构与语义信息过滤数据图中的节点。这些算法虽然从不同角度增加剪枝过滤效果,从而改善了搜索效率,却很难在合理时间内对大规模数据图进行子图匹配求解。为了扩大求解规模,VF3 算法[7]在VF2的基础上依据查询图节点的匹配点在数据图中的出现概率计算匹配顺序,并引入分类概念,将节点按照度与标签进行分类,进一步减少了搜索空间。CFL-Match[8]算法提出分解查询图延迟笛卡尔积,以有效减少冗余的中间结果的产生,采用辅助数据结构CPI存储候选集中的部分连边。CECI[9]算法则将数据图划分为多个嵌入簇并进行并行处理,采用剪枝技术对嵌入簇反复修剪,得到辅助数据结构CECI。虽然构造辅助数据结构提高了在大规模数据图中的搜索效率,却存在消耗大量的内存空间和预处理时间的问题。

为了平衡子图匹配求解算法的时间复杂度和空间复杂度,从增强过滤效果、优化匹配顺序和减少冗余搜索3方面出发,提出了基于图神经网络的子图匹配符号(symbol solving algorithm for subgraph matching based of graph neural network,简称SSMGNN)算 法。不 同 于 VFGCN 算 法[14],SSMGNN算法通过引入图神经网络(graph neural networks,简称GNN)[15-16]提取节点的特征向量,以该向量作为过滤条件来缩小节点候选集。其次,SSMGNN算法在文献[9]的基础上,综合考虑了节点候选集的大小、节点度数以及待匹配节点的邻居中已匹配节点数等信息,给出了一种新的优化匹配顺序。同时,将引入的代数决策图(algebraic decision diagram,简称ADD)[17]作为图的存储结构,采用符号ADD操作对子图匹配求解,在求解过程中,提出一种新的编码使得并行处理候选区[18]的划分,从而减少冗余搜索。因符号ADD 是隐式存储,使得SSMGNN算法能在较小的存储空间中操作较大规模的图。

1 相关概念

定义1 标签图G=〈V,E,L,l〉,其中:V表示图G的节点集合;E表示图G中所有的边集;L表示节点标签集合;l表示标签映射函数:V→L。

定义2 给定数据图g=〈Vg,Eg,Lg,lg〉与查询图q=〈Vq,Eq,Lq,lq〉。图q与图g存在子图同构关系,当且仅当存在一个单射函数f:Vq→Vg满足:

1)∀u∈Vq,∃f(u)∈Vg,lq(u)=lg(f(u));

2)∀(u,u′)∈Eq,∃(f(u),f(u′))∈Eg.

定义3 ADD 是表示基于变量序π:x1＜x2＜…＜xn的一族伪布尔函数fi:{0,1}n→S的一个有向无环图,它满足[19]:

1)S为ADD代数结构的有限值域,且S∈Z。

2)ADD中的节点分为根节点、终节点和内部节点3类。

3)终节点集合记为T。对任意t∈T,均被标识为值域S中的一个元素是s(t)。每个非终节点u具有四元组属性(fu,nvar,l,h),其中:fu表示节点u所对应的伪布尔函数;nvar表示节点u的标记变量;l表示节点u的nvar=0时,节点u的0-分支子节点;h表示节点u的nvar=1时,节点u的1-分支子节点。

4)图中的每个节点u对应唯一一个函数fu。

5)图中任意一条从根节点到终节点的路径中,所有变量均按变量序π的顺序出现,且仅出现一次。

2 基于图神经网络的子图匹配符号算法

基于图神经网络的子图匹配符号算法由3个步骤组成,即生成候选集、生成匹配顺序和求解子图同构,算法的基本框架如图1所示。首先,从提升过滤效率的角度出发,引入图神经网络提取图节点的特征向量,并以该向量作为过滤条件为查询图生成候选集。其次,根据查询图节点的候选集、度以及查询图的层次结构等属性对匹配顺序进行优化。最后,使用ADD表示候选集与图,并结合ADD 符号操作在数据图中以查询图的半径为范围并行构建候选区,并在候选区中采用回溯算法进行求解。

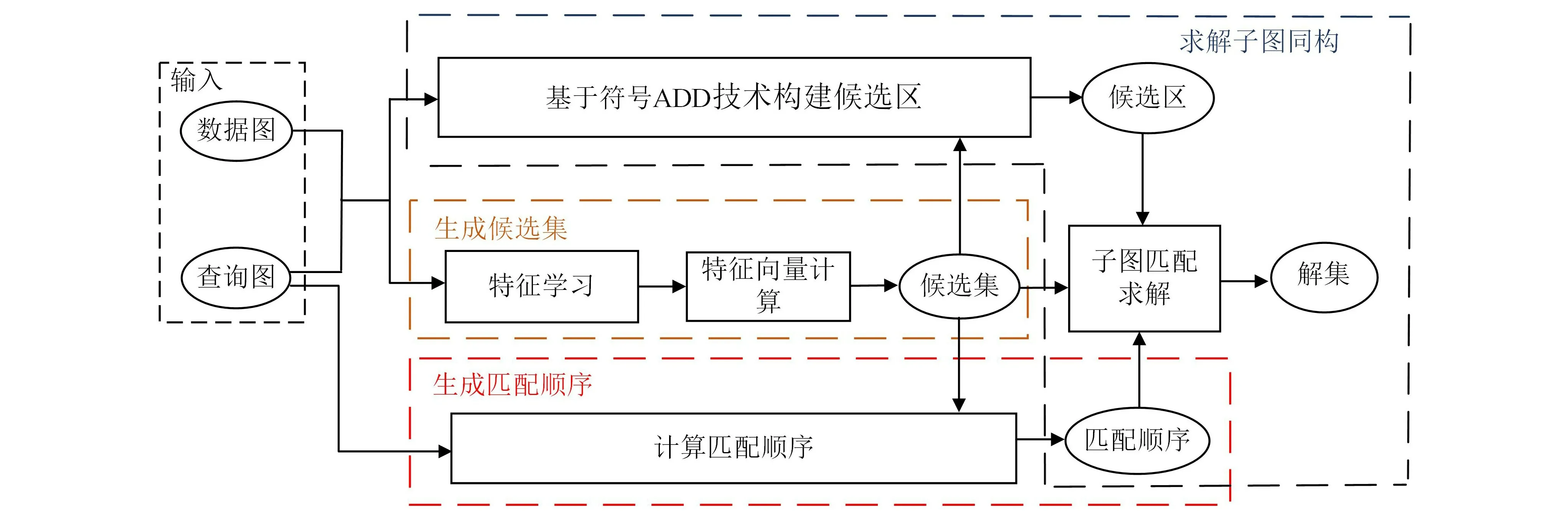
图1 SSMGNN算法的基本框架

2.1 生成候选集

目前,大量的子图匹配算法可分为过滤与验证2个步骤,其过滤阶段将在数据图中探索查询图每个节点可能匹配的节点,这些匹配节点的集合称为该节点的候选集。在验证阶段,根据候选集的节点在数据图中进行搜索,从而得到子图匹配的可行解集。为了尽可能减少候选集中错误候选节点的数量,现有的子图匹配算法大多基于节点的标签与度信息对候选集进行过滤,却忽略了节点的局部邻域结构与属性信息。为此,用图神经网络对图的节点进行邻域信息聚合,得到节点特征向量,使得节点包含更多的局部信息,从而提升过滤效率。

首先利用图注意力网络[20]学习数据图与模式图的节点特征,得到其表示向量。其次,在文献[21]提出的子图预测函数的基础上,设计了函数p(xv,xu),该函数通过比较节点的表示向量中每个位置的数值大小来判断2个节点的邻域结构是否可能存在包含关系,如式(1)所示。

其中:xv为节点v的特征向量;xv[i]表示xv的第i个值;d为特征向量的维度。通过式(1)对数据图与查询图的每个节点的特征向量中每个位置的数值进行比较。若p(xv,xu)为1,表示节点v的节点邻域结构可能包含节点u的邻域结构,从而检查节点u与v的标签与度是否一致,一致则将节点v加入节点u的候选集。若p(xv,xu)为0,则说明2个节点的邻域信息不存在包含关系,从而节点v不能成为节点u的候选点。

2.2 确定匹配顺序

在子图匹配求解过程中,查询图节点匹配顺序的选择对搜索效率有着严重影响。如图2所示,查询图q中的每个节点在数据图g中的候选节点表示为(u1,{v1,v2})、(u2,{v3,v90})、(u3,{v5,v6,v91})、(u4,{v7,v8,…,v91})、(u5,{v4,v88,…,v89})。针对查询图q,若给定匹配顺序P1={u4,u1,u5,u2,u3},根据回溯搜索算法在数据图g中进行搜索求解,其搜索次数为1 280次,几乎需要遍历整个搜索空间。若匹配顺序为P2={u1,u2,u3,u5,u4},其搜索次数为175次。由此可见,合适的匹配顺序能够有效减少搜索次数,从而提高搜索效率。

图2 查询图q与数据图g

因此,将综合考虑查询图节点的候选集、度数以及查询图的结构3个方面来对查询图匹配顺序进行优化。具体来说,优先匹配候选集小且度数大的节点,可降低中间结果的产生。由于在子图搜索的过程中会检查待匹配节点与已匹配节点的结构关系与查询图q是否一致,优先考虑与已匹配节点连边多的节点,也可提高搜索效率。因此,综合考虑节点候选集的大小、节点度数以及待匹配节点的邻居中已匹配数量,并选择两者之和的最大的节点作为下一个匹配节点,具体如式(2)所示。

其中:｜·｜表示取集合中元素的个数;C(u)表示节点u的候选集;d(u)表示节点u的度;N(u)为节点u的邻居节点集合;M为已匹配节点的集合且初始值为空集;｜N(u)∩M｜为节点u的邻居中已匹配的数量。第一个匹配节点称为根节点,因为选择根节点时M为空集,从而根据节点度数与节点候选点的数量的比值进行选择,优先选择两者比值大的节点作为根节点,并将根节点加入M。下一个节点的选择,将会在节点度数与节点候选点的数量的基础上考虑该节点与M中节点的连边数量,若度数与节点候选点的数量的比值相同,则优先选择与M连边的节点作为下一个节点。以此类推,确定所有节点的匹配顺序。

2.3 候选区

文献[9]指出在候选区中进行子图匹配能够有效减少搜索次数,并且在构造候选区的过程中可以进一步对候选集进行过滤。为了得到数据图中的所有同构子图,在构建候选区时,根节点的候选集中所有节点分别作为中心节点,在数据图中挖掘大小与查询图半径相同的子图作为候选区。然而,这一做法造成不同的候选区之间存在许多相同的节点和边,导致需要花费大量的空间来存储。ADD 是一种高紧凑、易操作的数据结构,可以对数据进行压缩存储,是克服存储容量限制的一种有效措施。因此,引入了符号ADD,将其作为候选区的存储结构,并且可以并行地在数据图中进行搜索,得到所有候选区,有效解决了存储空间问题,且提高了构建候选区的效率。

2.3.1 ADD表示

给定图G,其节点数量｜V｜=n,首先对图G的节点与边进行编码。节点编码可采用长度为m=log2n的二进制串X=(x1,x2,…,xm)表示[22-23]。边代表节点与节点间的二元关系,因此边记为(X,Y)=(x1,x2,…,xm,y1,y2,…,ym),其中:X表示边的起始节点;Y表示边的终节点。将数据图g的边集Eg转化为ADD表示,记为Eg(X,Y),查询图q边集的ADD 表示记为Eq(X,Y)。候选集的ADD表示与边相同,记为(X,Y)=(x1,x2,…,xm,y1,y2,…,ym),其中:X表示查询图的节点;Y表示数据图的节点。候选集的ADD表示记为C(X,Y)。

为了压缩存储空间并实现并行搜索,将所有候选区合并存储。因此,候选区的ADD 表示添加变量Z,以区分不同的候选区,记为(Z,X,Y)=(z1,z2,…,zm,x1,x2,…,xm,y1,y2,…,ym)。其中:Z表示候选区区分标志;X表示候选区中边的起始节点;Y表示候选区中边的终节点。如图2(b)所示,R1与R2为数据图中的2个候选区,分别由根节点u1的候选点v1与v2作为起始节点与该区的区分标志,数据图g的节点数n=97,则m=7,通过Z变量编码0000001与0000010来区分R1与R2候选区。

2.3.2 候选区构建

候选区的构建首先需要基于2.1节计算得到根节点,并通过根节点得到查询图的广度优先搜索树与查询图的半径r。其次,根节点的候选点分别作为起始节点vs并作为区别候选区的标志。然后,根据vs在数据图中利用广度优先搜索构造以r为范围的候选区,在此过程中,每层候选区中的节点都会与查询图中该层节点的候选集做集合操作,以保留候选区中属于候选集的节点。构建候选区的伪代码如算法1所示。

算法1的第1行函数GetRootCand是将根节点root(X)与查询图节点的候选集C(X,Y)做ADD符号操作,返回根节点的候选集Croot(X)。第3行函数Region Mark是通过符号操作构造以Croot(X)中的每个节点为起始点与区分候选区节点的候选区Rtmp(Z,X)。第5～8行是一个以查询图的半径为范围的for循环,根据广度遍历搜索,在数据图中一层一层地往下搜索并更新候选区。其中第6行函数Get-Layer Node是为了得到候选区的第i+1层的节点,首先通过查询图操作得到第i+1层的节点并得到该层节点的候选集,用该候选集过滤数据图操作得到第i+1层的节点,从而得到候选区的第i+1层的节点Ln(Z,X)。第7行函数UpdateRegion为更新增加候选区的边集,将候选区R(Z,X,Y)中第i层节点与Ln(Z,X)节点的连边和每个候选区中Ln(Z,X)节点间的连边加入候选区R(Z,X,Y)。第8行函数UpdateParameter为更新数据图在不同候选区中已经遍历过的节点、查询图已经遍历的节点、已经分区待操作的数据集中的节点和查询图中待操作的节点,更新后进入下一次for循环。第9行返回候选区R(Z,X,Y)。

2.4 SSMGNN算法

结合符号ADD技术构建候选区并进行求解,给出基于图神经网络的子图匹配符号算法(SSMGNN)。该算法主要步骤为:第1步产生候选集,利用GNN对图节点邻域信息聚合并得到特征向量,使用该向量计算得到查询图候选点。第2步优化匹配顺序,为后续的搜索匹配做准备。第3步构建候选区,在数据图中利用符号ADD操作构建候选集的各个候选区域。第4步子图匹配求解,结合ADD操作与回溯搜索进行求解。SSMGNN 算法的伪代码如算法2所示。

算法2第1行函数NodeEmbedding用于对查询图的节点进行邻居信息聚合并表示为特征向量。第2行函数ComputeCand使用式(1)计算数据图与查询图的节点特征,得到查询图节点在数据图中的候选集。第3行Order函数用于优化模式图的节点匹配顺序。通过候选集和查询节点的度等信息确定查询图的根节点root。以root为起始点对查询图进行广度遍历搜索,并对每层的节点进行排序,该排序按照已匹配节点的连边、候选集大小与度等条件得到最终的匹配顺序。第4行函数CreateADD是将排序后的节点,查询图的边集、候选集与根节点转化为ADD图表示。第5行函数ADDPartition使用ADD 操作在数据集构建多个候选区R(Z,X,Y),具体过程在算法1中给出。第7行函数GetRootCand通过ADD符号操作返回root的候选集Croot(X)。第8～14行是以Croot(X)的节点为起始节点的每个候选区进行子图同构匹配。其中第9行函数ChooseRegion将选择Croot(X)中的一个节点与候选区R(Z,X,Y)做符号操作,并返回其中的一个候选区Ri(X,Y);第10～13行Cheak Region函数是检查Ri(X,Y)的可行性,查看每个查询点的候选集在Ri(X,Y)中是否为空,若为空,则说明该区域无解,需要重新选择一个候选区,否则,使用第13行函数Match进行求解,在Ri(X,Y)中按照order的匹配顺序对变量进行赋值,采用回溯搜索算法寻找可行解并将其加入解集;第14行返回所有可行解。

3 实验结果及分析

实验环境为Core i5-1038NG7 CPU@2.00 GHz,16 GiB内存,操作系统为Windows 10 64位,编译语言为Python和C/C++。实验使用的2个公开数据集分别是human和yeast。其中human数据集为人类蛋白质相互作用的数据图,由86 282条边、4 674个节点和44 个不同的标签组成的无向图;yeast数据集包含了12 519条边、3 112个节点与71个不同的标签。对于每个数据集,构造4种不同的查询集,分别为Q4、Q8、Q16、Q32,其中Qi表示包含i个节点的查询图的查询集。每个查询集包含50个具有相同数量节点的连通图。由于VF3算法是单机上非常高效的算法,其性能优于VF2[4]、L2G[24]、LAD[11]和RI[10]算法,因此本实验将与VF3算法进行比较。实验结果中,平均时间为每组查询图得到子图同构所有解计算的总时间与查询数量的商,平均时间作为评估指标更能体现子图同构算法的时间效率。

实验结果如图3所示,SSMGNN-yeast与VF3-yeast分别表示SSMGNN 算法与VF3算法在yeast数据集上的平均运行时间;同理,SSMGNN-human与VF3-human分别表示2种算法在human数据集上的平均运行时间。通过实验对比可知:

图3 human与yeast数据集的实验结果

1)当查询集为Q4时,VF3算法在2个数据集上的平均求解时间较少,优于本算法,其原因是在算法执行过程中,构建ADD 需要消耗一定的时间,并且SSMGNN 算法利用图神经网络提取节点的邻域信息作为过滤条件,在模式图较小的时候,其邻域包含信息较少,从而过滤效果并不明显。然而,随着查询图规模的增加,SSMGNN 算法的平均时间性能明显优于VF3算法,且时间增幅小于VF3算法,这表明本算法在处理较大规模的查询图时更具有优势。尽管当查询图规模增加时,2个算法的时间复杂度都明显增加,但是本算法通过优化匹配顺序与增加节点邻域信息作为过滤条件,有效减小了搜索空间,使得时间效率得到提升。

2)VF3算法在human数据集的求解时间比在yeast数据集上耗时更长。其原因是,human数据集是稠密图并且标签更少,VF3算法在human数据集需要花费更多的时间进行搜索求解。但是,SSMGNN 算法在稠密和稀疏数据集上的求解时间相当。由此表明,本算法不仅在稀疏图上能够高效求解,并且在稠密图上的求解效率远超于VF3。

查询集的聚合时间如表1所示,对于不同规模下的查询图,邻域信息聚合的平均时间都在0.001 2 s左右,由此可见,图神经网络在4～32个节点的规模下都能够花费非常少的时间对节点的邻域信息进行特征提取。

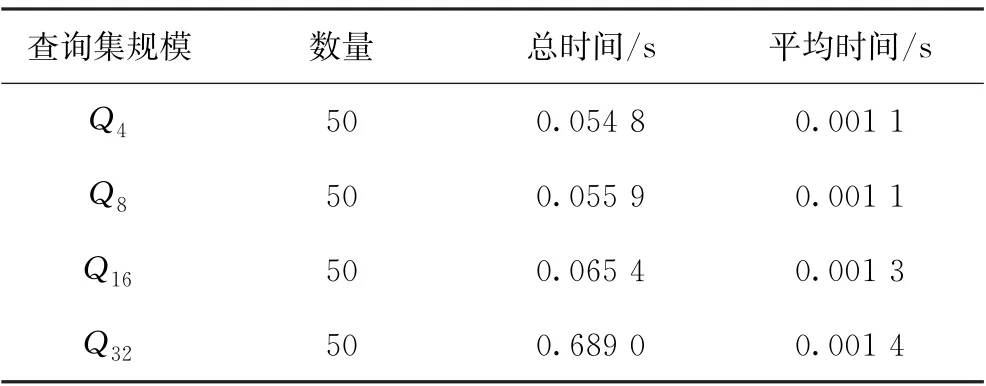
表1 查询集的邻域聚合时间

在实验的过程中发现,对于邻域信息聚合时,并不是聚合越多的邻域信息,其过滤效果越好,在聚合时所选择的k值(节点的k步邻居)为2时,效果最好。原因是human与yeast数据集中的查询图的半径范围几乎不超过3,当k值越大时,会使得所有节点的邻域信息趋于一致,从而降低其过滤效果。

4 结束语

提出了一种结合图神经网络与符号代数决策图解决子图同构问题的算法。该算法利用图神经网络聚合节点邻居信息,提高了过滤候选节点的效率,并且基于候选集、度与子图的结构等特征提出了一种优化的匹配顺序。其次,构建了关于数据集、查询图与候选集的ADD 图,使用符号ADD 操作实现了在单机上并行划分候选区并进行回溯求解。实验结果表明,该算法有效提高了子图同构问题的求解效率。在未来的工作中,将研究如何使用符号ADD并行求解子图同构问题,进一步提高在单机上的求解效率。