基于最短长链接优先选择的VLSI阵列重构算法

莫福浩, 钱俊彦

(桂林电子科技大学 计算机与信息安全学院,广西 桂林 541004)

随着超大规模集成(VLSI)技术和晶圆规模集成(WSI)技术的发展,集成系统得以在芯片上构建。然而,随着VLSI阵列中处理单元(PE)密度的增加,VLSI阵列发生故障的概率也随之增加,从而导致处理器的计算能力和稳定性受到影响,进而影响整个集成系统的正常工作。因此,需要采用容错技术对阵列进行重构来提高阵列的可靠性。

网络拓扑结构的VLSI重构技术主要有冗余法和降阶法[1]2种。在冗余法中,集成系统存在部分备用的处理单元,当系统中出现故障处理单元时,可用备用的处理单元对故障的处理单元进行替换;在降阶法中,系统的元件均以统一的方式进行处理,无额外的备用元件,这种方法使用阵列中尽可能多的无故障处理单元来重构目标阵列,从而提高无故障处理单元的使用效率。

在过去的几十年间,二维处理器阵列的重构策略被广泛研究。Kuo等[2]提出了二维处理器阵列下3种路由重构方案:1)行、列旁路;2)行旁路和列重路由;3)行、列重路由,同时证明了阵列的重构问题是NP完全问题。Low等[3]用GCR算法构建包含所选行的最大目标阵列。基于片上网络阵列,Xiang等[4]提出了一种新的用于全网单播组播核心测试的传输容错路由算法,并基于重叠虚拟网络策略,提出了片上网络无死锁自适应路由方案;此外,Xiang等[5]提出了一种高性能自适应路由策略,有效降低了芯片网络的功耗;基于重复转向模型,Cai等[6]提出了基于无死锁自适应方案的三维片上网络路由算法。重构方案主要从时间、规模、内部链接长度等方面对阵列进行优化。在降低阵列重构时间方面,Wu等[7]用并行算法减少阵列的构建时间;Qian等[8]提出了一种智能搜索算法,有效提升了阵列的重构效率;Qian等[9]提出了一种可满足最大功率效率VLSI阵列重构的有效方法。在减少阵列长连接方面,Srikanthan等[10]通过重构紧耦合目标阵列优化了阵列的长连接;肖汉鹏等[11]设计了紧耦合阵列的整数规划模型;Qian等[12]提出了一种构造高性能VLSI子阵列的有效多重最短增广路径算法;黄弼胜等[13]利用网络流模型减少阵列的连接长度。在扩大阵列规模方面,王意萍等[14]基于整数规划思想获取了最大规模阵列;Qian等[15]在行和列重路由方案下重构了VLSI子阵列的数学模型;Ding等[16]提出了在行和列重路由下重构二维网格连接VLSI子阵列的灵活方案;Qian等[17-18]利用网络流算法对阵列进行优化,并提出了一种新的算法,扩大了阵列的规模。白章顺等[19]提出了一种容错处理器阵列的重构抽象模型;胡佳等[20]提出了一种高性能阵列重构的SAT 描述模型;Wu等[21]将阵列的研究从二维阵列向三维阵列延伸;Jiang等[22]提出了一种高效的重构算法,降低了三维阵列中的连接长度;Jiang等[23]在取消限制补偿距离的条件下提出的FLX算法进一步扩大了获取的阵列规模,并在FLX 算法的基础上,基于分治策略的思想,提出了RIL算法,减少了阵列中的长链接数。然而,由于RIL算法在重构逻辑列的过程中需要对局部区域内所有的节点进行访问,在一定程度上影响了阵列的重构时间,降低了重构效率。因此,为了减少构建阵列过程中对节点的访问数,加快阵列的重构速度,在RIL算法的基础上,提出了一种基于最短长链接优先选择原则的重构(acceleration of RIL,简称ACRIL)算法。

1 二维阵列结构与问题描述

1.1 阵列结构

在二维VLSI阵列中,制造产生的原始阵列用H表示,阵列大小为m×n,其中m、n分别为原始阵列的行数和列数。假设p为原始阵列的故障密度,0≤p≤1,则原始阵列中出现故障的处理单元的个数N表示为N=(1-p)×m×n。故障的处理单元表示不能对数据进行处理或者从其他处理单元获取数据的处理单元。原始阵列经过重新配置后获得的阵列称为逻辑阵列,用T表示,阵列大小为m′×n′(m′≤m,n′≤n),逻辑阵列中不包含故障的处理单元。原始阵列和逻辑阵列中的行(列)分别称为物理行(列)和逻辑行(列)。原始阵列的物理结构如图1所示。

图1 VLSI阵列体系结构

每个开关有4种链路状态。每个处理单元都可通过改变路由开关的链接状态来改变处理单元之间的连接方式。ei,j、e′i,j分别为物理阵列、逻辑阵列中处于位置(i,j)的处理单元,其中i为处理单元的行号,j为处理单元的列号。原始阵列有2种基本的重构方案,分别是行旁路方案和列重路由方案。在行旁路方案中,ei,j-1可直接通过改变内部开关连接状态,绕过故障的处理单元ei,j,直接与ei,j+1相连,同理,列旁路方案的定义与之类似。在列重路由方案中,ei+1,j为故障处理单元,可通过外部开关直接连接到ei,j′,其中j-j′＜d,d为补偿距离,通常限制为1,从而能够有效保证硬件实现低功耗。同理,行重路由方案的定义与之类似。

根据补偿距离的定义,每个处理单元的上相邻节点集合和下相邻节点集合分别记为A-(u)、A+(u),且定义如下:

定义1 对于行中的每个无故障处理单元,

1)A-(u)={v:v∈Ri-1,v为无故障处理单元,且col(u)-col(v)≤1},2≤i≤m。

2)A+(u)={v:v∈Ri+1,v为无故障处理单元,且col(u)-col(v)≤1},1≤i≤m-1。

3)对于任意的v∈A+(u)(A-(u)),当col(u)-col(v)=-1时,v称为u的左下(上)邻接处理单元;当col(u)-col(v)=0时,v称为u的中下(上)邻接处理单元;当col(u)-col(v)=1时,v称为u的右下(上)邻接处理单元。

一个二维逻辑阵列有6种可能的链路方式,根据链路使用的开关数,可分为短连接与长连接。只使用一个开关来连接目标阵列中的处理单元的链路方式称为短连接,而使用2 个开关的链路方式称为长连接。

定义2 长连接数量最少的阵列称为高性能逻辑阵列(HPTA)。

1.2 问题描述

在行旁路和列重路由条件下对二维处理器阵列的重构问题进行研究,研究内容包括寻找高性能的无故障目标阵列。

问题1 给定一个规模大小为m×n的带有故障节点的网状连接处理器阵列,找到长链接数目最小的无故障高性能目标阵列。

2 ACRIL算法介绍

RIL算法通过运用分治策略的思想解决了不限制补偿距离条件下的问题1。为了优化RIL算法的效率,采用ACRIL算法,通过减少对无故障节点的访问次数,重构局部优化逻辑列,以降低逻辑阵列的重构时间。

ACRIL算法的求解结果如图2所示。该算法主要分为3个子过程:Up_Process表示第一个公共处理单元到第一行的子逻辑列求解过程;Down_Process表示最后一个公共处理单元到最后一行的子逻辑列求解过程;Shest_Process表示公共处理单元之间的子逻辑列求解过程。图2中的数字表示处理单元的长连接。

图2 ACRIL算法的求解结果

ACRIL算法的整体思路如下:

1)在一次迭代过程中,找到左右2条逻辑列的交点,并将交点放入交点集合中。

2)利用智能搜索算法分别求解Up_Process、Down_Process及Shest_Process三个子过程,每个子过程获得一段路径。

3)将这3个子过程获得的路径进行合并,得到一条完整的路径,此路径即是所要求的一条逻辑列。

4)将新获取的逻辑列作为新的边界,继续重构逻辑列,重复1)、2)、3)过程。

算法1 ACRIL算法

输入:m×n的原始阵列。输出:m×k的目标阵列。1)根据主阵列,依次分别从左至右和从右至左的方式重构逻辑列。

2)直到从2个方向构建的逻辑列连接到相同的节点,形成公共区域。在逻辑列的公共区域构建具有最短长连接的逻辑列。

将3个部分获得的路径合并形成一条完整的路径P=P1∪P2∪P3。

3)以新构建的逻辑列作为新的边界,重复步骤1)、2),直到所有的逻辑列构建完毕。

Shest_Process子过程主要运用启发式搜索思想进行求解,其求解过程描述如下:

输入:2个公共节点S、T。

输出:S、T之间的一段路径P。

1)设置2个列表,分别为开放列表与关闭列表。

2)遍历节点,计算当前节点的权值,根据情况将节点放入相应的列表中;当节点已位于开放列表时,重新计算权值。

3)当开放列表为空时,表示子过程执行完毕。求解子过程的伪代码如下:

计算u的权值,将u放入开放列表;

从下邻接集合中去除u。

Up_Process和Down_Process子过程的求解方式与子过程Shest_Process类似。

3 实验与分析

为验证ACRIL算法的有效性,用C++语言实现了该算法,还原了现有的重构算法RIL,并将2种重构算法进行对比。为保证实验数据具有可比性和可靠性,2种重构算法均在相同的实验环境下运行。执行程序的实验配置环境为Inter®CoreTM3.10 GHz 的 CPU 和8 GiB RAM,操 作 系 统 为Windows 10。

RIL算法与ACRIL 算法的访问节点数的对比如图3所示。图3中,在64×64规模下的原始阵列的错误率分别设置为1%、5%、10%、15%。从图3可看出,在错误率为1%的原始阵列中,RIL算法对阵列中的节点访问数为5 091,而ACRIL算法对阵列中的节点访问数为3 989;在错误率为10%的原始阵列中,RIL算法对阵列中的节点访问数为5 191,而ACRIL算法对阵列中的节点访问数为3 573。2种重构算法的实验数据比较结果表明,相较于现有的重构算法RIL,ACRIL算法能在一定程度上减少阵列在重构逻辑列的过程中对节点的访问数,提高阵列的重构效率。

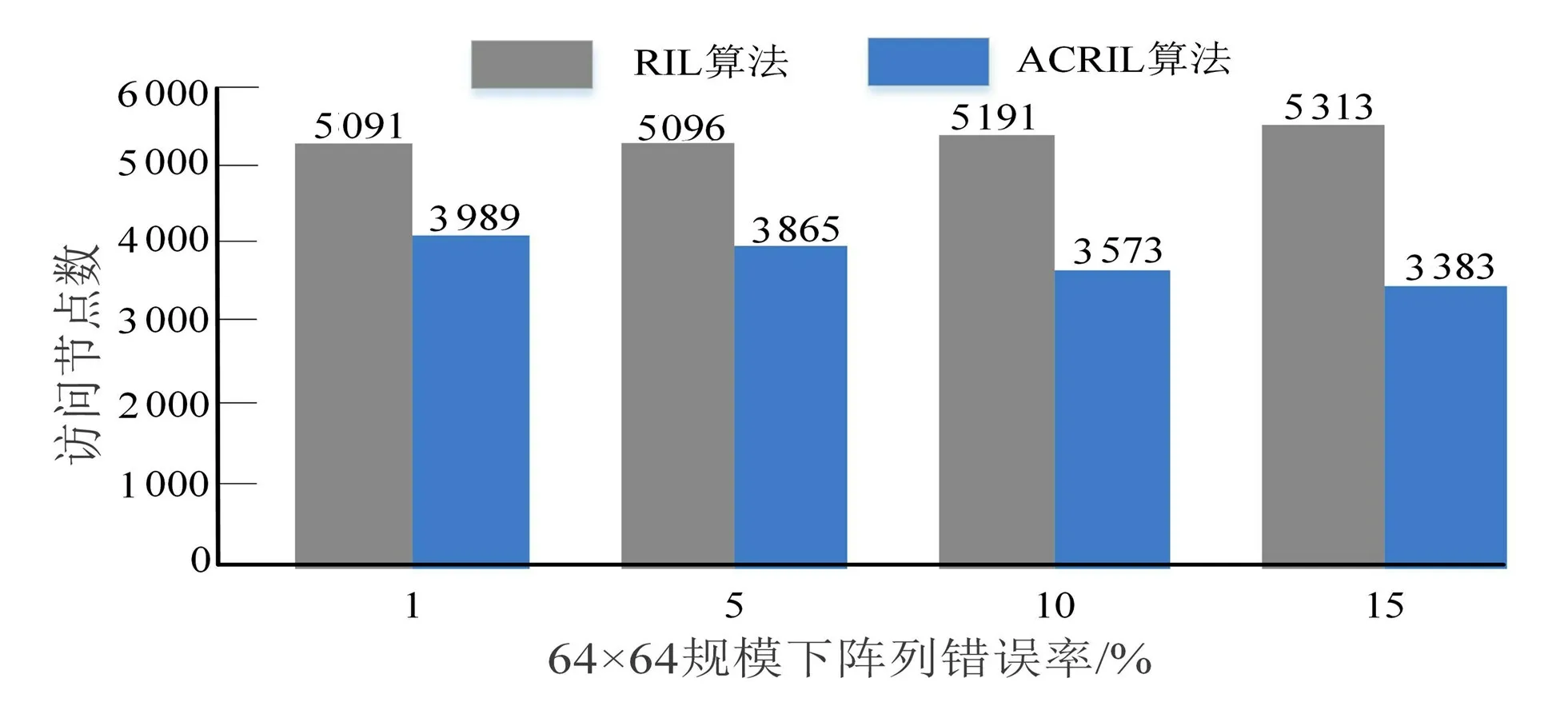
图3 RIL与ACRIL算法的访问节点数对比

RIL算法与ACRIL算法性能指标如表1所示。从表1可看出,两者在相同错误率条件下都可获取相同规模的目标逻辑阵列,且相比于RIL算法,ACRIL算法的阵列重构时间更短,这表明阵列从故障状态恢复的效率更高。例如,在错误率为1%、规模为32×32的原始阵列中,RIL算法的重构时间为674 ms,而ACRIL算法的重构时间为574 ms,重构效率提高了14.83%;在错误率为5%,规模为48×48的原始阵列中,RIL算法的重构时间为956 ms,而ACRIL算法的重构时间为821 ms,重构效率提高了14.13%。这表明ACRIL算法的运行性能明显优于RIL算法。

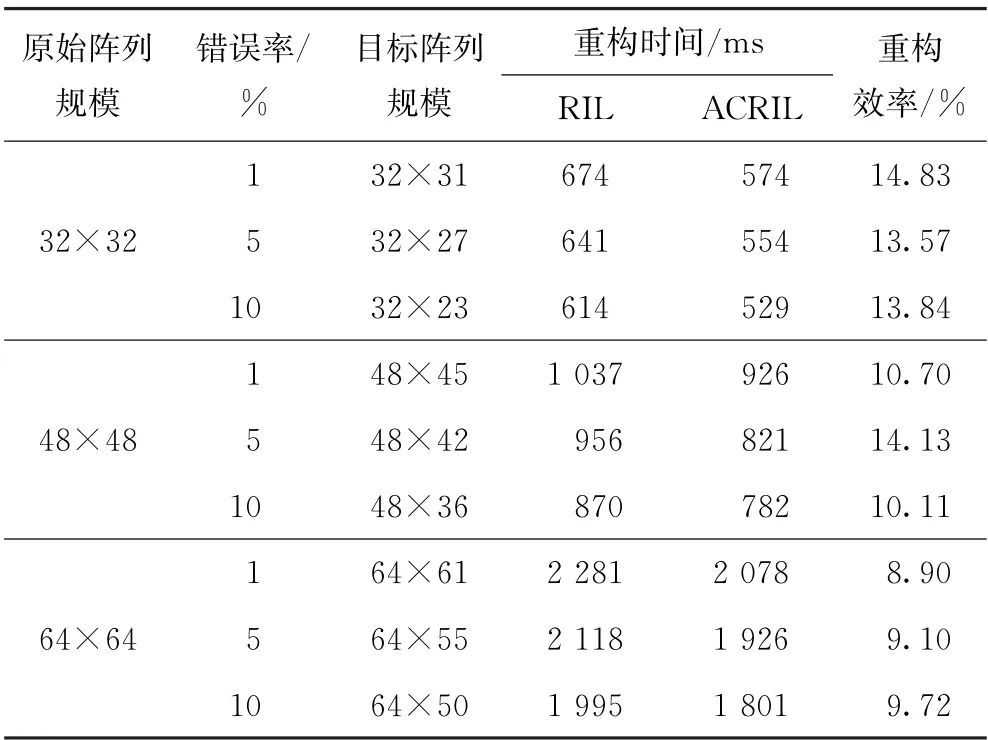
表1 RIL与ACRIL算法的性能指标

4 结束语

基于现有的重构算法,提出了一种通过减少处理单元的访问次数,进一步提高原始阵列重构速度的方案。实验结果表明,与现有的重构算法相比,该算法显著减少了处理单元的访问次数,减少了重构时间,降低了运行时的性能开销。本研究未考虑在构建阵列过程中逻辑列的选择对阵列规模的影响。今后的研究将着重于考虑新的改进算法,为可降阶的VLSI阵列的重构提供更好的性能优化。