井筒温度对含缺陷套管抗挤强度的影响
2022-11-05周传喜田海锋刘先明
周传喜 田海锋 郭 伟 管 锋 刘先明
(1.长江大学机械工程学院 2.中石化胜利石油工程有限公司井下作业公司)
0 引 言
石油钻采过程中,套管一直处于恶劣的环境中,在复合载荷和腐蚀性介质接触的作用下,易造成套管磨损和腐蚀,严重的磨损和腐蚀会造成油井减产、停产,甚至弃井,带来重大的经济损失[1-5]。
针对含缺陷套管的抗挤强度问题,许多学者对此进行了研究。高连新等[6]运用数值模拟与试验方法,得出套管抗挤毁强度与内壁磨损程度之间的关系。严攀等[7]建立了磨损套管-水泥环-围岩组合体力学模型,得到最大外挤力和套管强度与不均匀磨损深度之间的规律。针对弯曲套管磨损抗挤强度问题,学者们多采用解析法和数值模拟法对其抗挤强度进行研究[8-10]。练章华等[1]建立了单腐蚀坑缺陷和双腐蚀坑缺陷有限元模型,发现了腐蚀坑之间会产生交互作用的规律。刘文红等[11]通过试验研究了不同钢材力学性能随温度变化的规律,结果表明,管材的抗拉强度和屈服强度均随着温度升高而降低,而其断后伸长率和断面收缩率变化均不大。尹虎等[12]比较了常规水力压裂和大型水力压裂过程中钢材的受力情况,结果表明,井底温度对高钢级套管的抗挤强度影响较小,而对低钢级套管抗挤强度影响较大。
综上可知,现有关于套管抗挤强度的研究均单独针对缺陷或温度的影响而开展,对缺陷和温度共同作用下套管的抗挤强度变化研究鲜有提及。为此,有必要开展缺陷和温度共同作用下套管抗挤强度研究。笔者在套管抗挤强度分析的基础上,建立了磨损套管和腐蚀套管有限元模型,分析了套管磨损量、壁厚、腐蚀坑深度和腐蚀坑半径对套管抗挤强度的影响,并依据分析结果建立了N80钢级套管抗挤强度预测模型。研究结果可为套管设计和现场应用提供指导。
1 套管抗挤强度理论
在研究含缺陷套管抗挤强度时,将套管视为无初始椭圆度的均匀厚壁圆筒,其受内压和外压共同作用[13]。根据拉梅公式,厚壁圆筒上任意半径r处的受力为:
(1)
(2)
式中:σr为径向应力,MPa;σθ为周向应力,MPa;r1为套管内半径,mm;r2为套管外半径,mm;r为套管轴心到管壁上任意一点的距离,mm;pi为套管内压力,MPa;po为套管外压力,MPa。
图1为含缺陷套管平面模型图。图1中δ为套管壁厚,mm;h为腐蚀坑最大深度,mm。由拉梅公式可推出API套管抗挤强度计算式[14]:
(3)
式中:pco为抗挤强度,MPa;YP为套管材料最小屈服强度,MPa;DC为套管外径,mm。

图1 含缺陷套管平面模型Fig.1 Planar model of defective casing
本文采用塑性挤毁失效准则,通过改变套管外压,直至管体发生塑性变形,即材料达到屈服极限,此时的外载荷即为抗挤强度[15]。
2 有限元建模及分析
2.1 材料参数与边界条件
本文以工程常用的N80套管为例,材料密度7 850 kg/m3,泊松比0.3。图2为套管磨损有限元模型。通过预定义场对磨损套管模型施加温度,设置随时间变化的均匀载荷,给套管外壁施加均匀载荷边界。图3为腐蚀坑套管有限元模型。为提高计算效率,建立完整套管的模型,如图3a所示;并对腐蚀坑网格进行加密,如图3b所示。同磨损套管模型一样,预定义场对腐蚀套管模型施加温度,通过给套管外壁施加随时间变化的均匀载荷,套管两端采用固定约束,周向采用对称约束。
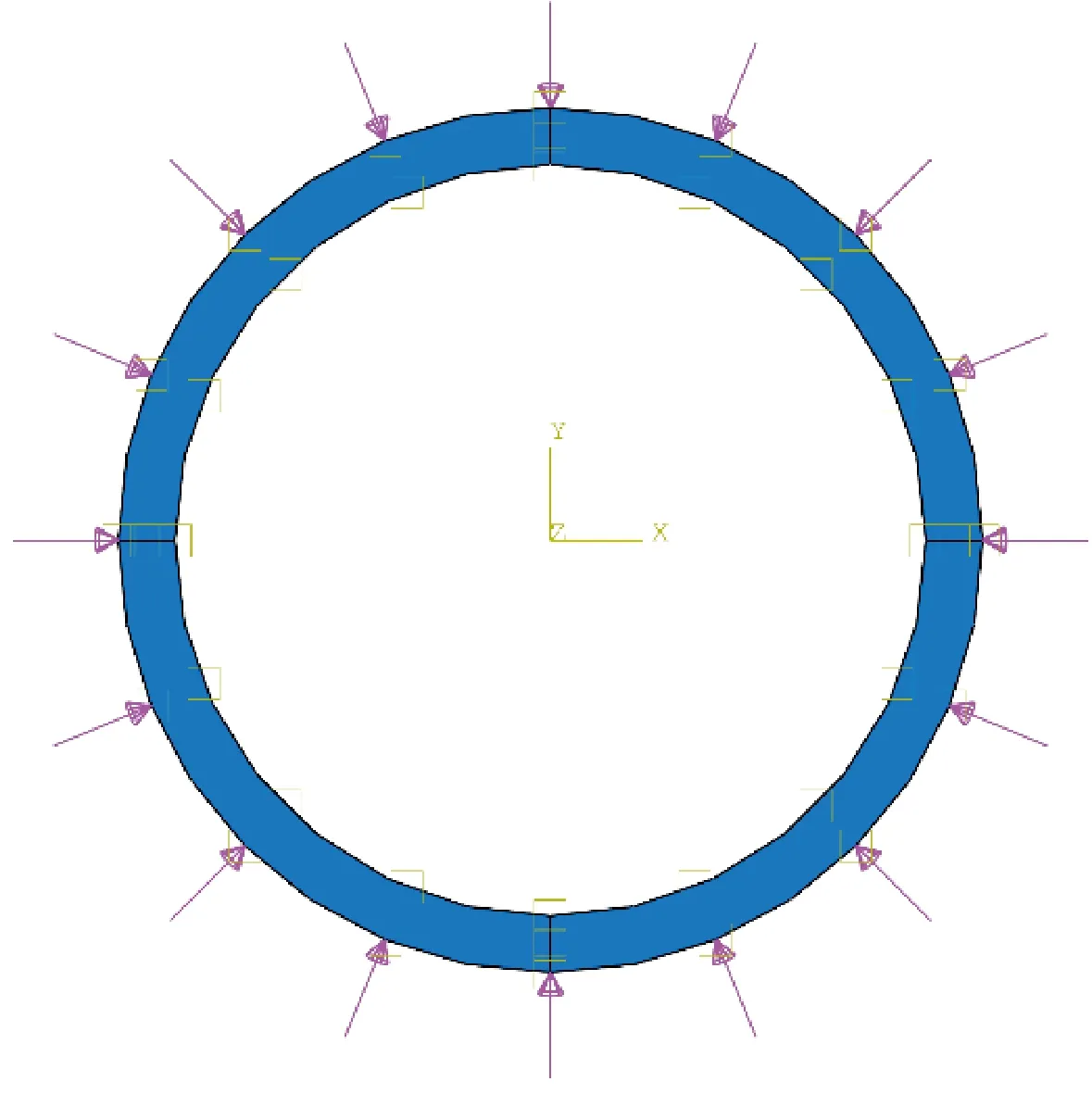
图2 套管磨损有限元模型Fig.2 Finite element model of casing wear
N80套管屈服强度σN80、弹性模量EN80和热膨胀系数λN80随温度T的变化关系[16]为:
σN80=604.759 6-0.2152T
(4)
EN80=(2.132 080-0.002 590 2T)×102
(5)
λN80=(-0.000 431 63T2+0.224 82T-
3.664 74)×10-6
(6)

图3 腐蚀套管有限元模型Fig.3 Finite element model of corroded casing
2.2 模型验证
通过API套管抗挤公式计算结果对数值模拟结果进行验证。建立套管的二维模型,套管外径193.7 mm,壁厚9.52 mm,屈服强度600.45 MPa,泊松比0.3,弹性模量208 GPa。在非线性有限元分析中,给套管外壁施加均布载荷,直至套管内部的最大von Mises等效应力等于管材的屈服强度为止[16]。
对无磨损套管抗挤强度进行分析,有限元方法得到套管抗挤强度为57.02 MPa,API套管抗挤公式计算结果为55.91 MPa,抗挤强度误差为1.99%,满足现场应用要求,表明此方法可以用于套管抗挤强度的校核计算。对磨损率为40%的套管进行有限元计算,抗挤强度为17.60 MPa,与无磨损套管抗挤强度相比,套管抗挤强度出现明显下降,下降了69.13%。
2.3 含缺陷套管有限元建模
根据套管损坏的形式可将缺陷套管分为两类:磨损套管和腐蚀坑套管。磨损套管是由于钻柱在井下运动的不确定性,导致套管磨损形状的不确定。以月牙形磨损最为典型[17],因此本文以月牙形磨损套管为研究对象。针对壁厚为9.52、12.70和14.27 mm的3种套管,与套管摩擦的钻杆选用常规的ø88.9 mm钻杆;套管磨损率分别取套管壁厚的0%(无磨损)、10%、20%、30%和40%。
通过文献调研[18],CO2腐蚀坑大多呈浅球形,其他介质造成的腐蚀坑形状较为复杂,为方便研究,将腐蚀坑简化为规则的球形来模拟。建立套管的三维模型,模型长度取套管直径的10倍,壁厚为12.7 mm,腐蚀坑半径为3、4和5 mm,深度为1~5 mm,开展温度变化下腐蚀坑深度和半径对套管抗挤强度的影响规律研究。为避免边界条件对结果的影响,将腐蚀坑设定在套管中心部位。
2.4 含缺陷套管有限元分析
通过对磨损率40%、壁厚9.52 mm、套管外径193.70 mm的套管抗挤强度分析,得到磨损套管von Mises应力分布云图,如图4所示。通过应力云图分析:von Mises应力越大的区域,套管越快达到屈服阶段;磨损套管的最大von Mises应力出现在套管内部,并且位于套管壁厚最小处。在磨损区域,以壁厚最小为界限,von Mises应力向两边逐渐减小。
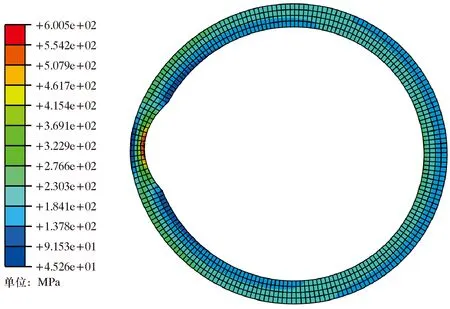
图4 磨损率40%时套管外挤作用下von Mises应力云图Fig.4 Von Mises stress cloud chart of casing with 40% wear rate under external pressure
3 套管抗挤性能参数影响分析
3.1 磨损对套管抗挤性能的影响
通过对磨损套管进行调研,磨损套管抗挤强度主要受壁厚和磨损率的影响。
3.1.1 磨损率
套管磨损率可通过壁厚的减小来表征。本文以外径193.70 mm套管和ø88.90 mm钻杆组合为研究对象,分析不同温度下套管磨损率对抗挤强度的影响,结果如图5所示。
由图5可知:相同磨损率下,套管抗挤强度随温度升高而单调递减;均匀增加磨损率时,温度由20 ℃升高至200 ℃,抗挤强度分别下降4.89、3.59、2.70、1.94和1.58 MPa;同一温度下,套管抗挤强度不断减小且下降幅度也随之变小,以20 ℃为例,等量增加磨损率,抗挤强度分别下降19.95、13.73、10.58和5.98 MPa。根据相同壁厚条件下温度对套管搞挤率的影响(见图6),套管抗挤强度随温度的变化率(抗挤率)只与温度有关。

图5 同一壁厚条件下温度对套管抗挤强度的影响Fig.5 Effect of temperature on collapsing strength of casing at the same wall thickness

图6 相同壁厚条件下温度对套管抗挤率的影响Fig.6 Effect of temperature on collapsing rate of casing at the same wall thickness
3.1.2 壁厚
分析不同壁厚套管抗挤强度,有助于在套管柱设计过程中针对不同地层深度选择合适的套管壁厚。
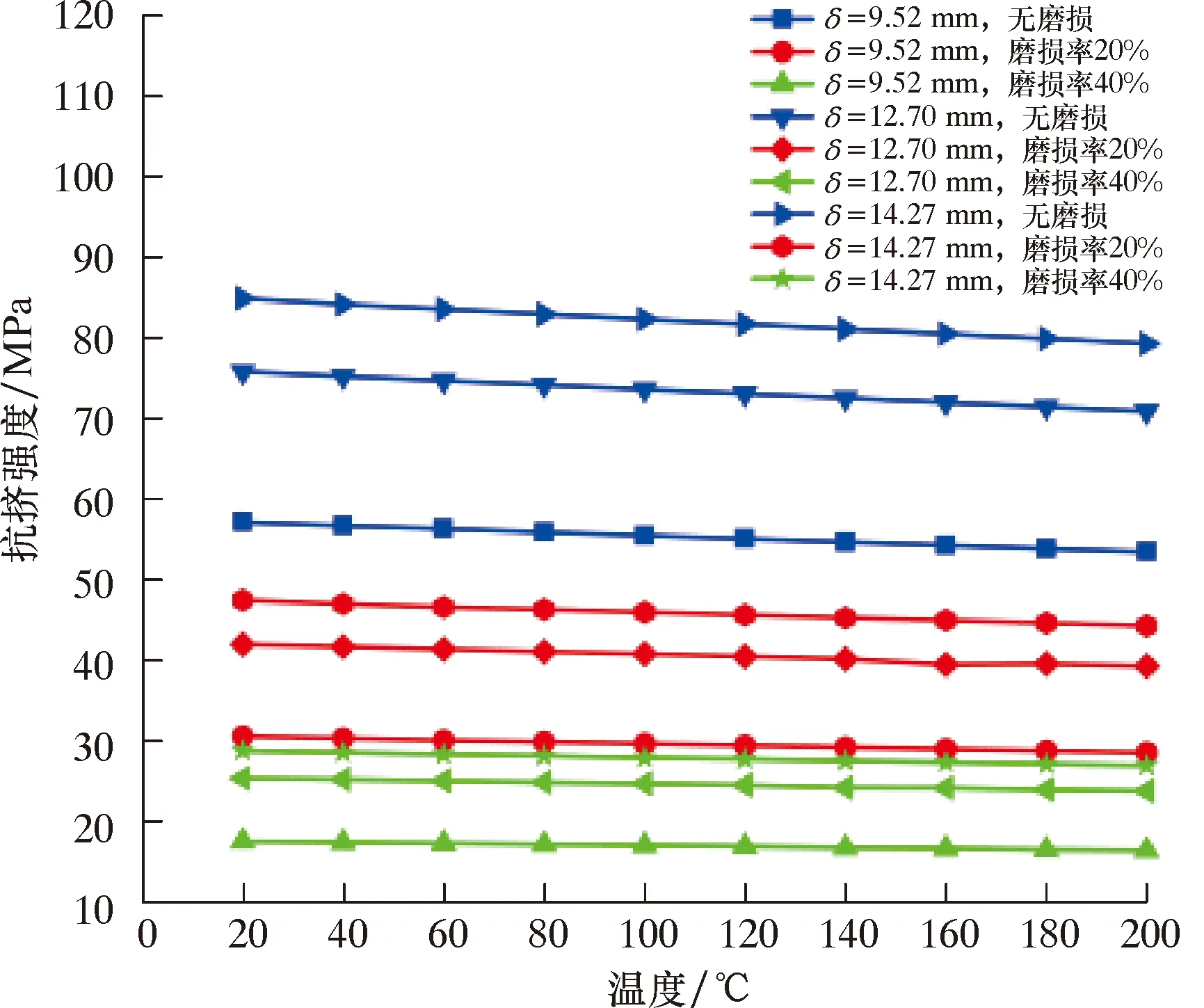
图7 不同壁厚条件下温度对套管抗挤强度的影响Fig.7 Effect of temperature on collapsing strength of casing at different wall thicknesses
图7为3种壁厚(δ=9.25、12.70、14.27 mm)N80套管的抗挤强度随温度变化规律。在磨损率一定时,温度从20 ℃增加到200 ℃,套管的抗挤强度随温度升高而下降。相应的抗挤率变化如图8所示。由图8可知,套管抗挤率的变化与套管壁厚及磨损率的大小无关,只与温度有关。抗挤率下降的幅度基本相同,与20℃相比200 ℃时的抗挤率下降了6.5%左右。
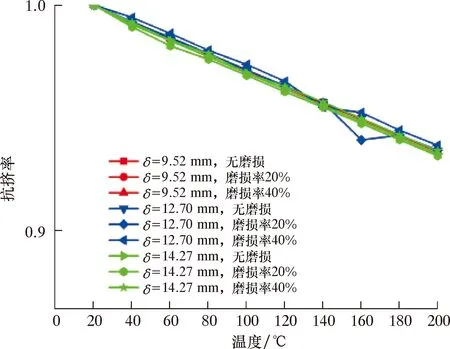
图8 不同壁厚下条件下温度对套管抗挤率的影响Fig.8 Effect of temperature on collapsing rate of casing at different wall thicknesses
3.2 腐蚀对套管抗挤性能影响
腐蚀坑对套管抗挤强度的影响因素主要为腐蚀坑半径和深度。
3.2.1 腐蚀坑深度
本节以腐蚀坑半径5 mm的腐蚀套管为研究对象,以温度和腐蚀坑深度为参数。
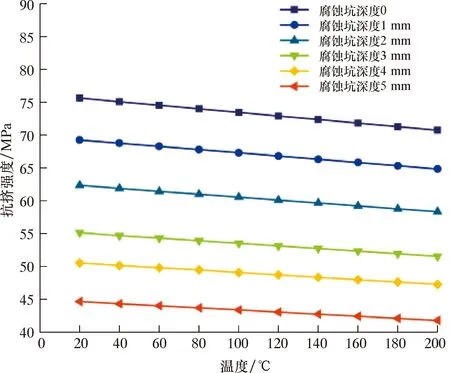
图9 同一腐蚀半径下温度和深度对抗挤强度的影响Fig.9 Effect of temperature and depth on collapsing strength at the same corrosion radius
同一腐蚀坑半径,不同腐蚀深度时套管抗挤强度随温度变化规律如图9所示。由图9可知:相同腐蚀坑深度下,套管抗挤强度随温度升高而降低;同一温度下,套管的最大抗挤强度随腐蚀深度的增加而减小。随着套管腐蚀坑深度的增加,套管抗挤强度下降幅度相对于套管磨损率变化对抗挤强度的影响小。对图9进一步研究,发现不同腐蚀坑深度下,在同一温度时套管抗挤率基本相同,如图10所示。

图10 同一腐蚀半径下温度和深度对抗挤率的影响Fig.10 Effect of temperature and depth on collapsing rate at the same corrosion radius
3.2.2 腐蚀坑半径
以温度、腐蚀坑半径和腐蚀坑深度为参数,开展抗挤强度研究。
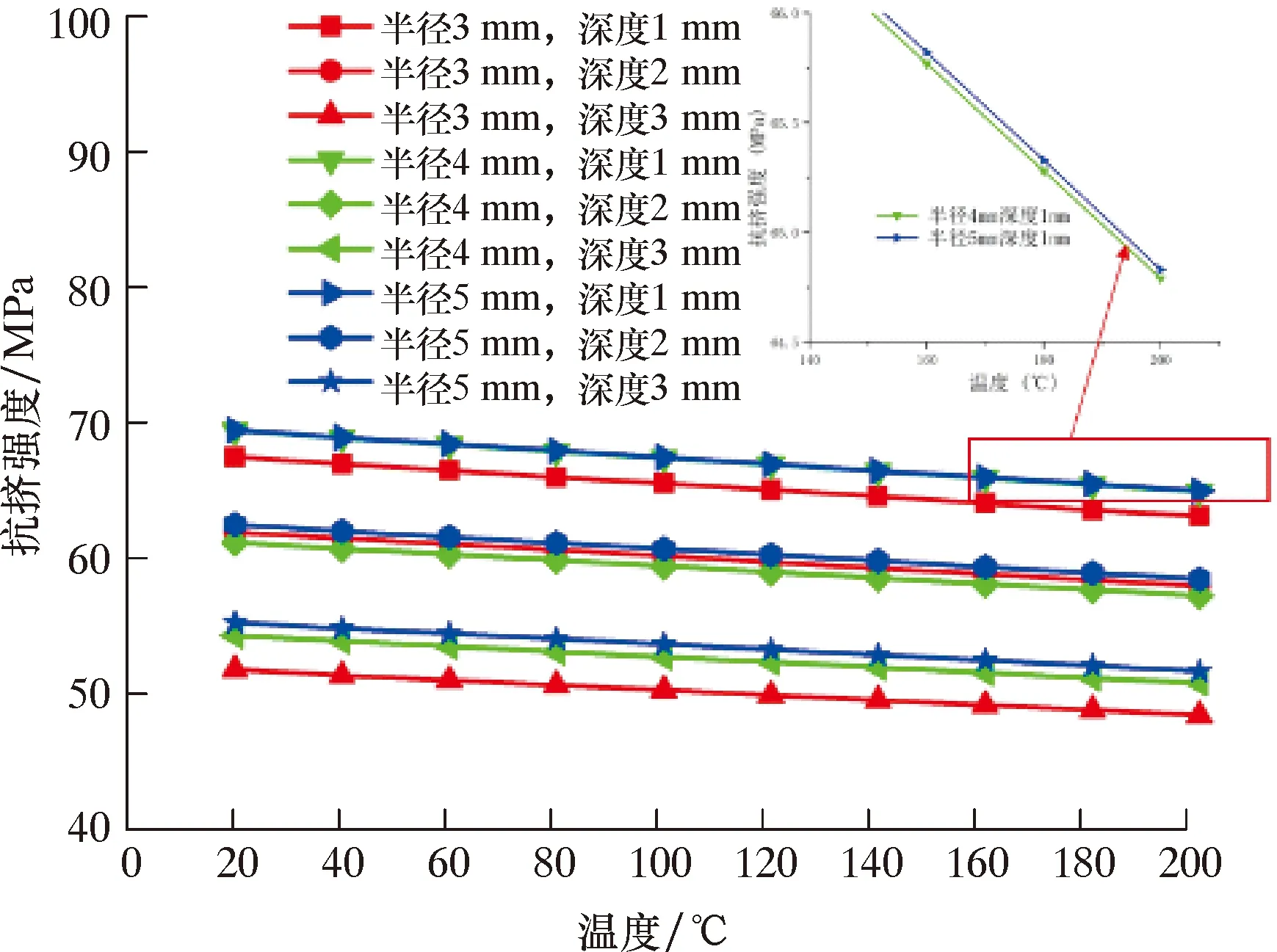
图11 不同腐蚀半径下温度对抗挤强度的影响Fig.11 Effect of temperature on collapsing strength at different corrosion radii
图11为腐蚀坑半径为3、4和5 mm时,抗挤强度随温度变化规律。由图11可知,在腐蚀坑半径不同,腐蚀坑深度相同时,随温度变化,不同腐蚀坑半径下抗挤强度变化不大。图12为不同腐蚀半径下温度对抗挤率的影响规律。由图12可知:在腐蚀坑深度为1 mm时,随着腐蚀坑半径的增大,抗挤率在温度从20 ℃变化到200 ℃时分别下降了6.43%、6.44%和6.44%;当腐蚀坑深度为2 mm时,抗挤率分别下降了6.44%、6.43%和6.46%;当腐蚀坑深度为3 mm时,抗挤率分别下降了6.52%、6.44%和6.49%。由此可知,在不同腐蚀坑半径下抗挤率下降的程度基本相同。
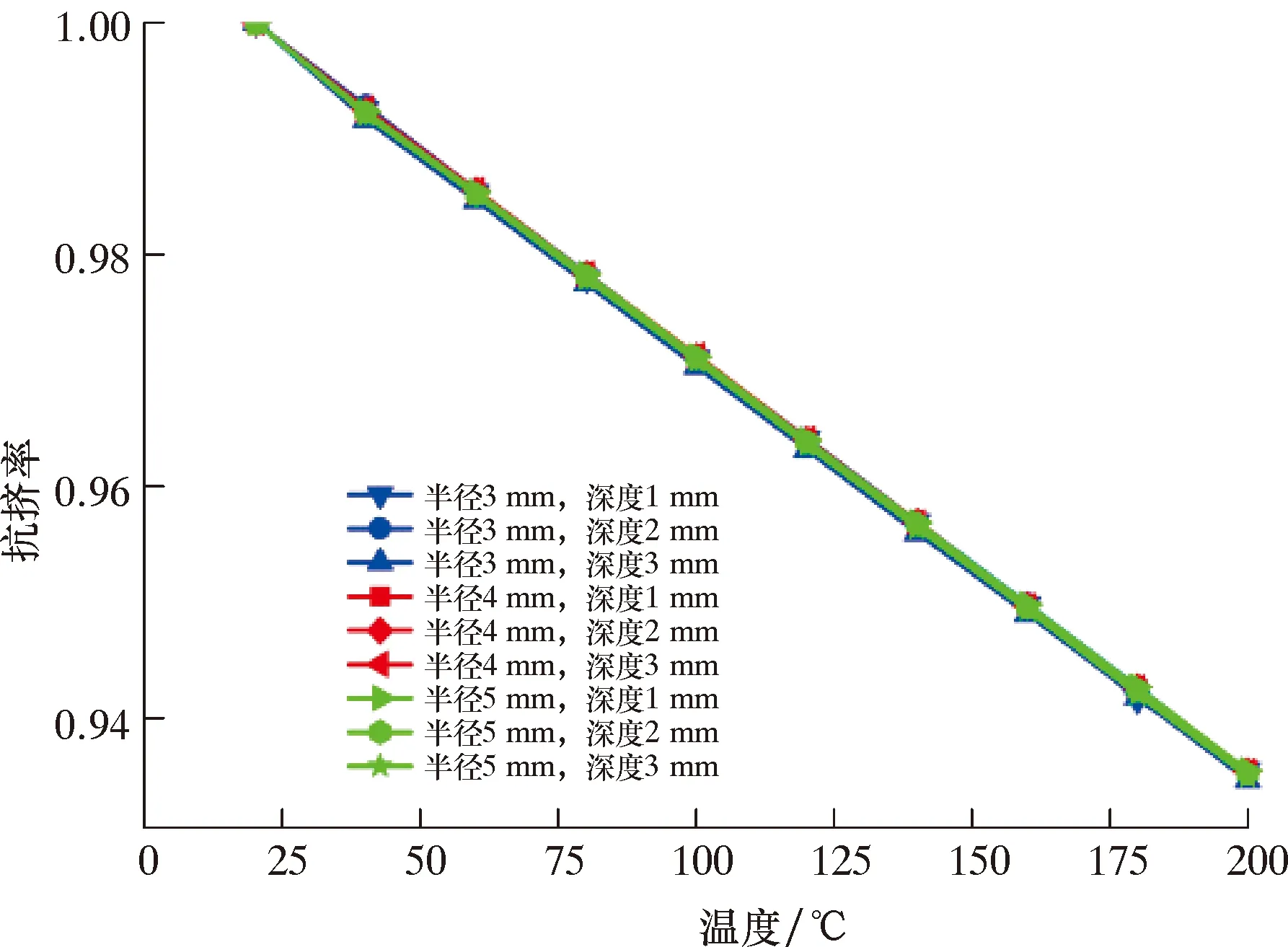
图12 不同腐蚀半径下温度对抗挤率的影响Fig.12 Effect of temperature on collapsing rate at different corrosion radii
4 预测模型
通过研究缺陷套管的壁厚、腐蚀半径、磨损率和腐蚀坑深度对抗挤强度的影响发现,抗挤率的变化只与温度有关[16]。由于高温的影响,钢材的各种性质发生变化,在实际过程中,需要对井内不同温度下的套管抗挤强度进行设计和校核。这里以N80钢材、外径193.70 mm和壁厚12.70 mm的套管为例,针对磨损套管和腐蚀套管的抗挤强度进行预测研究。
由前文可知,不同温度下套管抗挤强度可以表示为:
pT=kpyp
(7)
式中:pT为随温度变化的抗挤强度,MPa;k为套管强度随温度变化下降系数,即抗挤率;pyp为常温下套管抗挤强度,MPa。
通过SPSS软件对常温下磨损套管的抗挤强度数据进行拟合,即有:
pyp=75.40-213.62η+222.07η2
(8)
式中:η为磨损率。
对抗挤率进行拟合,得抗挤率k为:
k=-0.000 336T+1.006 7
(9)
将式(8)和式(9)代入式(7)可得:
pT=(-0.000 336T+1.006 7)2×(75.40-
213.62η+222.07η2)
(10)
表1为磨损套管抗挤强度有限元计算结果与预测结果对比表。
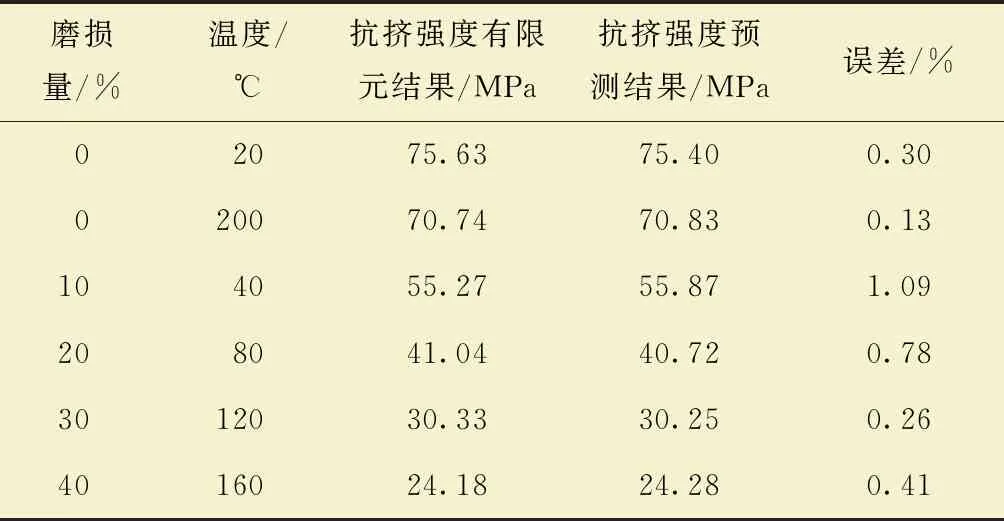
表1 磨损套管抗挤强度有限元结果和预测结果对比Table 1 Comparison of finite element results and prediction results of worn casing collapsing strength
同理可预测腐蚀套管抗挤强度随温度和腐蚀坑深度变化的关系。以腐蚀坑半径5 mm为例,对N80钢材、外径193.70 mm和壁厚12.70 mm的套管单坑腐蚀模型进行预测。由于抗挤率只与温度有关,所以k值相同,通过SPSS软件对数据拟合,于是有:
pT1=(-0.000 336T+1.006 7)×
(75.89-7.281h+0.209h2)
(11)
式中:h为腐蚀坑深度,mm;pT1为腐蚀套管随温度变化的抗挤强度,MPa。
表2为腐蚀套管抗挤强度有限元结果和预测结果对比表。
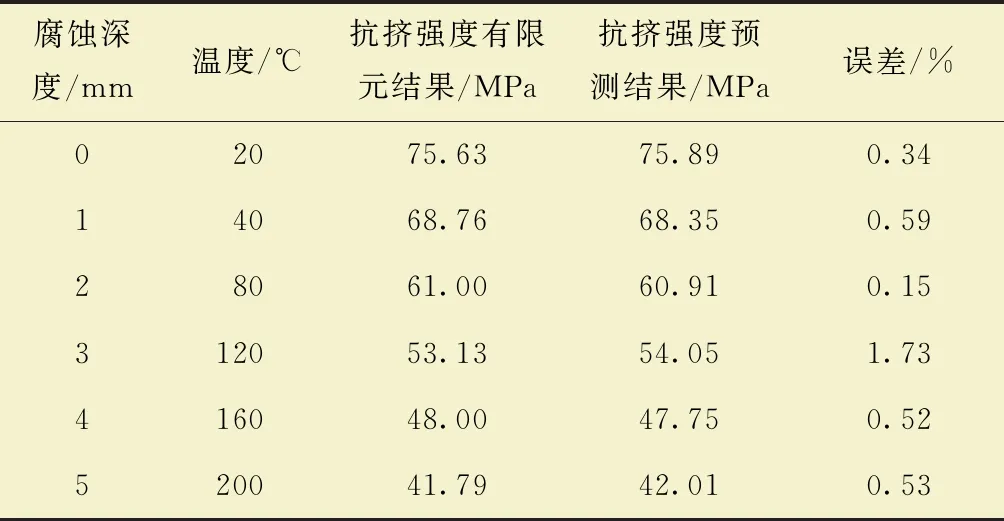
表2 腐蚀套管抗挤强度有限元结果和预测结果对比Table 2 Comparison of finite element results and prediction results of corroded casing collapsing strength
由表1和表2可知,套管磨损和腐蚀抗挤强度预测模型可靠性较高。对此方法进一步推广,在已知不同材料套管抗挤率和常温下缺陷套管抗挤强度的条件下,可预测不同材料缺陷套管抗挤强度,预测结果能为深井和超深井套管设计提供指导。
5 结 论
(1)根据API套管抗挤公式对数值模拟结果进行验证,验证了模型的可靠性,为温度变化条件下缺陷套管抗挤强度研究提供可靠基础。
(2)基于磨损和腐蚀坑模型分析得到套管抗挤强度随温度升高呈线性下降规律。相同温度下,套管磨损率等量增加,套管抗挤强度出现明显下降且下降幅度逐渐变小;相同温度下,保持套管腐蚀深度等量增加,套管抗挤强度持续下降,下降幅度相差不大。
(3)套管的壁厚、磨损率、腐蚀半径和腐蚀坑深度对抗挤率基本没有影响,抗挤率只与温度相关,200 ℃的抗挤率与20 ℃的抗挤率相比下降了6%~7%。
(4)推导出含缺陷套管抗挤强度预测模型,在20~200 ℃的温度范围内,预测模型可对磨损和腐蚀套管的抗挤强度进行预测。
