轮式牵引器耦合仿生驱动轮摩擦特性分析*
2022-11-05魏航信王金超
吴 伟 李 超 魏航信 王金超 王 方
(西安石油大学机械工程学院)
0 引 言
随着社会经济的快速发展,各行各业对石油的需求量日益增多,石油开采由中浅层向深层过渡已经成为必然趋势[1-2]。而深层石油开采过程中,井下总会存在不同程度的故障,需要进行一定的修井作业和测试工作才能保证石油天然气的正常生产[3],这就对测井仪器输送工具的输送能力提出了更高的要求[4]。
然而,现有水平井轮式牵引器存在以下问题:随着开采深度的增加,电缆与井壁间的摩擦阻力增大,如牵引器牵引力不足,则作业工具难以抵达目的层;由于轮齿与管壁存在摩擦,齿顶磨屑排出不及时易加剧磨损;驱动轮翻越障碍时,齿面残留磨屑容易划伤齿面等。因此,如何提高牵引器牵引力并延长驱动轮使用寿命具有重要的现实意义。
白相林和曾华军等[5-8]采用非线性约束优化的方法,通过确定驱动轮调节机构最优尺寸提高驱动轮的正压力来提高牵引力,但此方法提高牵引力的能力十分有限;秦浩等[9-10]通过改变驱动轮轮齿的齿形以提高犁沟摩擦因数,进而增加牵引力,但所采用的锥形和三棱柱形尖齿存在易磨损和强度不足等问题;郑杰等[11-12]设计了燕尾滑块锁紧机构来提高牵引器牵引力,但其伸缩前进无法保证牵引器的工作效率。
基于以上研究,针对牵引器牵引过程中遇到的问题,根据仿生学原理,笔者以蛤蜊、毛蚶外壳为仿生原型,应用其特有的生物学原理,通过改变驱动轮侧面与顶面形态,设计出一种牵引能力更强、脱黏减附能力优良、更耐用的仿生耦合驱动轮;并将传统驱动轮与仿生驱动轮的轮壁接触模型进行仿真对比,以期为后续轮式牵引器牵引能力的提高及驱动轮的优化设计提供一定的理论支持。
1 耦元设计与摩擦特性分析
1.1 驱动轮耦元设计
生活在沙滩砂质中的蛤蜊常年经受海砂的磨料摩擦,表面却完好无损,这是因为他们的壳体具有优良的耐磨性能。为了研究蛤蜊壳体耐磨损的生物耦合特性,文献[13]以蛤蜊外壳为仿生原型,采用逆向工程技术对蛤蜊和海贝壳体表面形态进行特征提取,并运用相应软件进行拟合处理,最终确定凸球形结构分布模型(如图1所示)。
凸球形耦元体有如下优点:
(1)齿面凸球形结构在驱动轮翻越管道接箍处台阶障碍时,一方面通过对管壁进行犁削从而增加摩擦过程中的运动阻力来增大摩擦因数;另一方面凸球形结构凸起部分和摩擦副凸起部分相互咬合,增大摩擦时的运动阻力,使得常温摩擦因数增大。因此有利于提高驱动轮的抓着力,提高牵引器越障能力。
(2)凸球形结构能够减少磨屑与齿面的接触面积及两接触面间的压力吸附点数,因此能够减少磨屑对齿面磨损及损伤。
(3)凸球形结构破坏了磨屑与齿面接触的连续性,使两者之间存在间隙空间,具有一定的撬离和剥离作用,使得磨屑难以在齿面附着。
毛蚶属于贝类的一种,其壳体也具有良好的抗磨损性能,根据其壳体表面分布的非光滑棱纹结构,从提高表面粗糙度与犁沟效应两方面着手来增大犁沟摩擦因数。本文提出基于毛蚶壳体的矩形与柱形仿生结构模型,如图2所示。
矩形与柱形耦元体优点:
(1)矩形与柱形体按照棱纹结构分布所形成的非光滑结构,不仅具有良好的耐磨性能,而且有着比凸球体更优良的摩擦特性,能够增加驱动轮牵引能力,其分布形式如图3所示。
(2)矩形与柱形体对于原齿面同样具有良好的撬离和剥离作用,能够在一定程度上减少轮齿齿顶磨损损伤,从而延长驱动轮的使用寿命,使驱动轮保持稳定的牵引能力。
(3)矩形与柱形体结构增加了齿面的表面积,因此具有良好的散热能力,有利于保持耦元体的耐磨稳定性。

图2 矩形和柱形结构分布模型Fig.2 Distribution models of rectangular and cylindrical structures

图3 仿生驱动轮模型Fig.3 Bionic driving wheel model
1.2 仿生驱动轮摩擦特性分析
根据现代摩擦理论,当硬质金属在软质金属表面滑动时,硬质金属凸起部分楔入软质金属表面使之产生塑性变形,并划出一条沟槽。当界面膜的抗剪切强度很低且表面黏着很小时,摩擦力中的犁沟项占主导地位。犁沟作用产生的摩擦力大小除与材料的性能有关外,还与凸体的几何形状密切相关[14]。因此将以上3种耦元结构分别运用到驱动轮侧面和顶面,当驱动轮在套管内行进时,对以上3种结构的摩擦特性做进一步分析。
1.2.1 凸球形结构摩擦特性分析
齿顶凸球形结构在管壁上滑动示意图如图4所示。
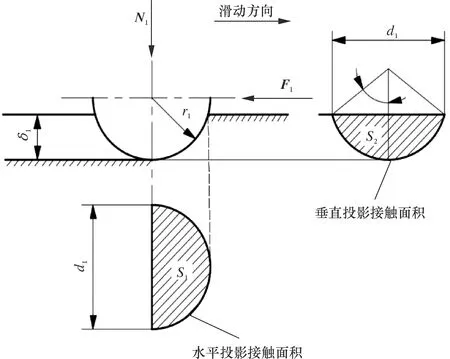
图4 齿顶凸球形结构在管壁上滑动示意图Fig.4 Schematic diagram for sliding of tooth top spherical structure on pipe wall
当驱动轮齿顶半球形结构压入管壁时,水平投影面积如下:
(1)
由弓形面积公式得垂直投影面积如下:
(2)
由于δ1的值为:
(3)
故得:
(4)
如果管壁金属的塑性屈服极限是各向同性,屈服极限为σ,则犁沟项摩擦阻力和法向力分别为:
(5)
(6)
式中:n表示与管壁相接触的半球形凸体的数目,D表示凸球半径r1的2倍。
故滑动摩擦因数为:
(7)
根据上式,由d1≤D可得摩擦因数f与凸球直径D、水平截面圆直径d的对应关系如图5所示。

图5 f与D、d的对应关系Fig.5 Correspondence among f,D and d
分析图5可知:当d=D/2时,摩擦因数f=0.212;当d=D时,f=0.424。由此可见,当半球形凸体曲率半径r较大且压入深度δ1较大时,d也较大,则滑动摩擦因数也较大,即摩擦力也较大,但是摩擦因数最大为0.424。
1.2.2 矩形与柱形结构摩擦特性分析
齿顶矩形、柱形结构在管壁上滑动示意图分别如图6和图7所示。

图7 齿顶柱形结构在管壁上滑动示意图Fig.7 Schematic diagram for sliding of tooth top cylindrical structure on pipe wall
当齿轮上表面为矩形结构并压入管壁产生摩擦时,其垂直和水平投影接触面积分别为:
(8)
S4=Lδ2
(9)
式中:δ2为矩形结构在管壁内的嵌入深度。
假设管壁的塑性屈服金属均质,其压缩屈服极限同为σ,则犁沟项摩擦阻力和法向力分别为:
(10)
F2=nLδ2σ
(11)
故矩形结构滑动摩擦因数为:
(12)
(13)
柱形结构摩擦因数为:
(14)
式中:D1为球径R的2倍;n为与管壁相接触的半球形凸体的数目。
若令D1=d2=1 mm,δ=δ3=δ2>0,即两者等宽且2种模型压入深度相同。由于摩擦因数为正值,所以取D1>δ3,再通过Matlab中Funtool工具绘制出两函数图像,并将两函数取差,所得图像如图8所示。

图8 f3-f2与δ的对应关系曲线Fig.8 Corresponding relation curve of and
由图8可知,在以上条件下f3>f2,因此半柱形结构比矩形结构有着更好的摩擦性能,所以驱动轮顶端结构选用半柱形结构能更好地提高牵引器的摩擦力。
摩擦因数f3与球径的对应关系如图9所示。由图9可知,柱形仿生结构的摩擦因数随着半径的增大逐渐减小并趋向于0.625。考虑到驱动轮顶部面积及仿生结构两列均匀排布等情况,此处选择圆柱半径R=0.3 mm,压入深度δ3=0.2时的仿生圆柱结构进行分析。此时摩擦因数f3=2.5,同时由分析可知,半径一定情况下,楔入深度越大,犁沟摩擦因数越大。

图9 f3与R的对应关系曲线Fig.9 Corresponding relation curve of f3 and R
1.2.3 仿生耦合驱动轮总体设计
根据上述3种结构模型,考虑到以下几种因素:3种结构中犁沟摩擦因数最大的是半柱体结构,其次是矩形结构,最后是球形结构;驱动轮与管壁接触时,矩形结构散热面积最大,其次是半柱体,最后是球体;根据接触面积,对磨屑的剥离减附能力方面,球体最强,其次是半柱体,最后是矩形。综合以上因素,驱动轮顶面耦元体选择圆柱体结构,侧面耦元体选择球体结构,最终确定仿生耦合驱动轮结构模型如图10所示。

图10 驱动轮仿生耦合模型Fig.10 Bionic coupling model of driving wheel
2 常规驱动轮摩擦特性分析
2.1 驱动轮轮齿力学分析
建立如图11所示的轮齿力学分析模型,对水平井牵引器驱动轮轮齿进行受力分析。由机械原理自锁的条件可知,驱动轮轮齿压入管壁时应该保持自锁状态,即轮齿的驱动力F与所受正压力WN的合力必须处于摩擦角ρ的范围以内,如此才可使牵引器按照预期的方向运动。由图11中的几何关系可得:
(16)
式中:ρ为摩擦角。

图11 轮齿力学分析模型Fig.11 Mechanical analysis model of wheel tooth
驱动轮和管壁间的接触与钢和软钢接触相同,因此取无润滑状态下驱动轮与管壁间的静摩擦因数μ为0.25[15],则摩擦角为:
ρ=arctanμ=14°
(17)
2.2 驱动轮摩擦特性分析
常规驱动轮摩擦特性分析如图12所示。

图12 常规驱动轮摩擦特性分析示意图Fig.12 Schematic diagram for frictional characteristic analysis of conventional driving wheel
根据图12,驱动轮轮齿垂直投影面积和水平投影面积分别为:
S7=L3(λ+e)
(18)
(19)
传统驱动轮轮齿的主要参数有:L3=10 mm,λ=0.735 mm。
其中:
L3=L2+2δ4tanγ
(20)
(21)
在管壁金属的塑性屈服极限为各向同性条件下,屈服极限为σ,则正压力N4及摩擦力F4分别为:
N4=σS7
(22)
F4=σS8
(23)
故滑动摩擦因数为:
(24)
联立上述各式,可得:
(25)
若驱动轮材质采用合金钢30CrNiMo,屈服强度为930 MPa。为了避免驱动轮轮齿受剪力而发生破坏,则轮齿所受剪应力τ必须低于其许用应力[τ],其中[τ]=σ/m,m为安全系数。即:
(26)
(27)
τ≤[τ]
(28)
为避免轮齿发生剪切破坏,取m=2.5时有[16]:
(29)
将式(17)代入式(29),可得:
74.6°≤χ≤130°
(30)
分析可知,f4随着χ增加而减小,因此当χ=74.6°时,f4最大。
当χ=74.6°,齿宽L3=10 mm,λ=0.735 mm,倾角取值范围为0°~70°时,可以得到f4与γ的关系,如图13所示。

图13 f4与γ的关系曲线Fig.13 Relation curve of f4 and γ
由图13可知,当γ=0时,f4存在极大值为0.23。令齿宽L3=10 mm,γ=0,χ=74.6°,压入深度δ4=0.2 mm,分析λ与f4之间的关系,结果如图14所示。
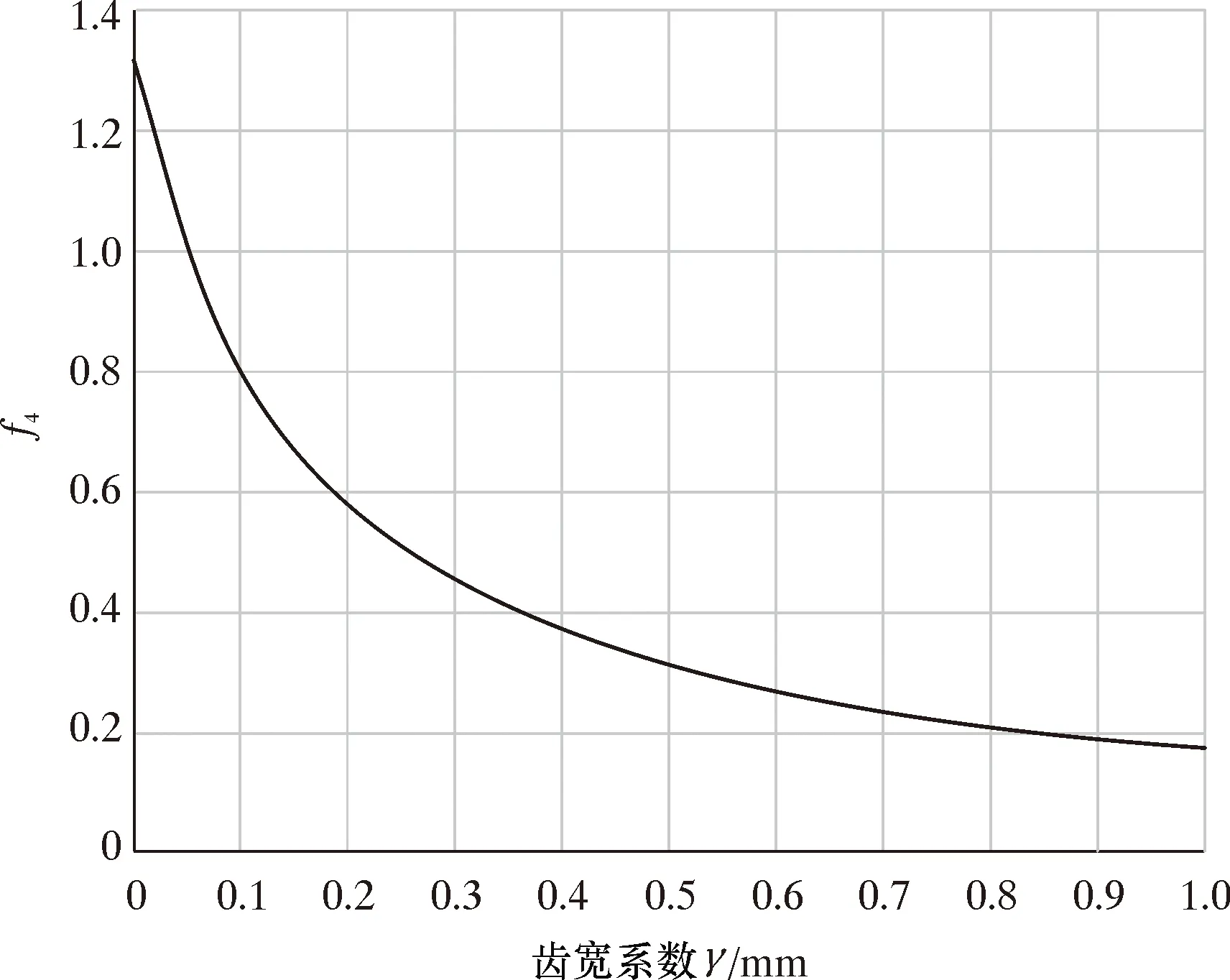
图14 f4与λ的关系曲线Fig.14 The relationship curve between f4 and λ
由图14可知,随着λ的增大,犁沟f4逐渐减小,当λ=0时,即驱动轮齿顶为三角尖顶时,f4存在最大值1.32。这是因为摩擦因数与轮齿压入时的垂直投影面积有关,随着压入深度的增加,垂直投影面积增大,所以摩擦因数增大。
2.3 结果分析
根据以上分析,当驱动轮楔入深度为0.2 mm,齿宽系数λ=0时,仿生耦合驱动轮犁沟摩擦因数为2.5,传统驱动轮的最大犁沟摩擦因数为1.6。可得:(2.5-1.32)/1.32=0.89。因此仿生耦合驱动轮比传统驱动轮的犁沟摩擦因数提高了0.89,即牵引能力提高了89%,牵引性能提高显著。
3 轮管接触强度有限元数值模拟分析
当驱动轮在一定的正压力作用下沿管壁行走时,轮齿在管道表面楔入时会产生犁沟效应,并在管道表面留下一定的沟槽。为了确保所提出的仿生耦合驱动轮不会影响套管的后续使用,其相比于常规驱动轮具有更为良好的牵引特性,本文通过ANSYS Workbench有限元软件,对常规和仿生驱动轮作用下套管的变形以及等效应力进行分析。
3.1 驱动轮模型建立及求解
为使仿真结果更为贴近实际,有限元仿真分析采用动态分析来模拟驱动轮的爬行过程。其中驱动轮d为60 mm,模数为2;管壁的几何模型为50 mm×80 mm×10 mm;柱形耦元数量为18个两列,尺寸 ø0.6 mm×1 mm,驱动轮模型如图15所示。驱动轮材料选择30CrMoTi,套管材料选择42CrMo,具体材料力学参数如表1所示。

图15 驱动轮轮壁接触模型Fig.15 Wheel-wall contact model of driving wheel
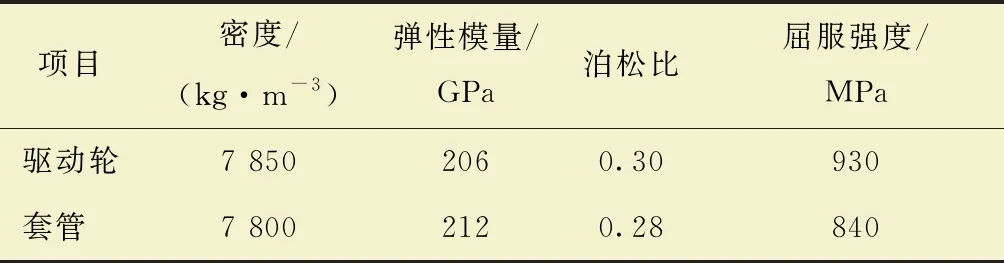
表1 驱动轮与套管材料力学参数Table 1 Mechanical parameters of driving wheel and casing materials
定义驱动轮与套管单元为六面体单元,对其接触面进行网格划分,网格大小为0.6 mm,有利于提高计算精度。将驱动轮与套管接触界面设置为接触面,接触类型为摩擦接触,对套管的边界进行固定,并限制套管所有自由度。
对驱动轮施加3 000 N的正压力,同时设定驱动轮转速为0.5 r/s来模拟爬行过程,而驱动轮本身不受约束。由于网格划分具有一定的不对称性,会使得驱动轮产生不符合实际的位移,从而导致求解不收敛,所以对驱动轮添加Weak Spring约束,以便求解能够快速并且收敛。
3.2 结果分析
图16和17分别表示在相同正压力条件下,2种驱动轮沿套管壁下行走时,单齿在套管表面所产生的位移场云图与应力场云图。
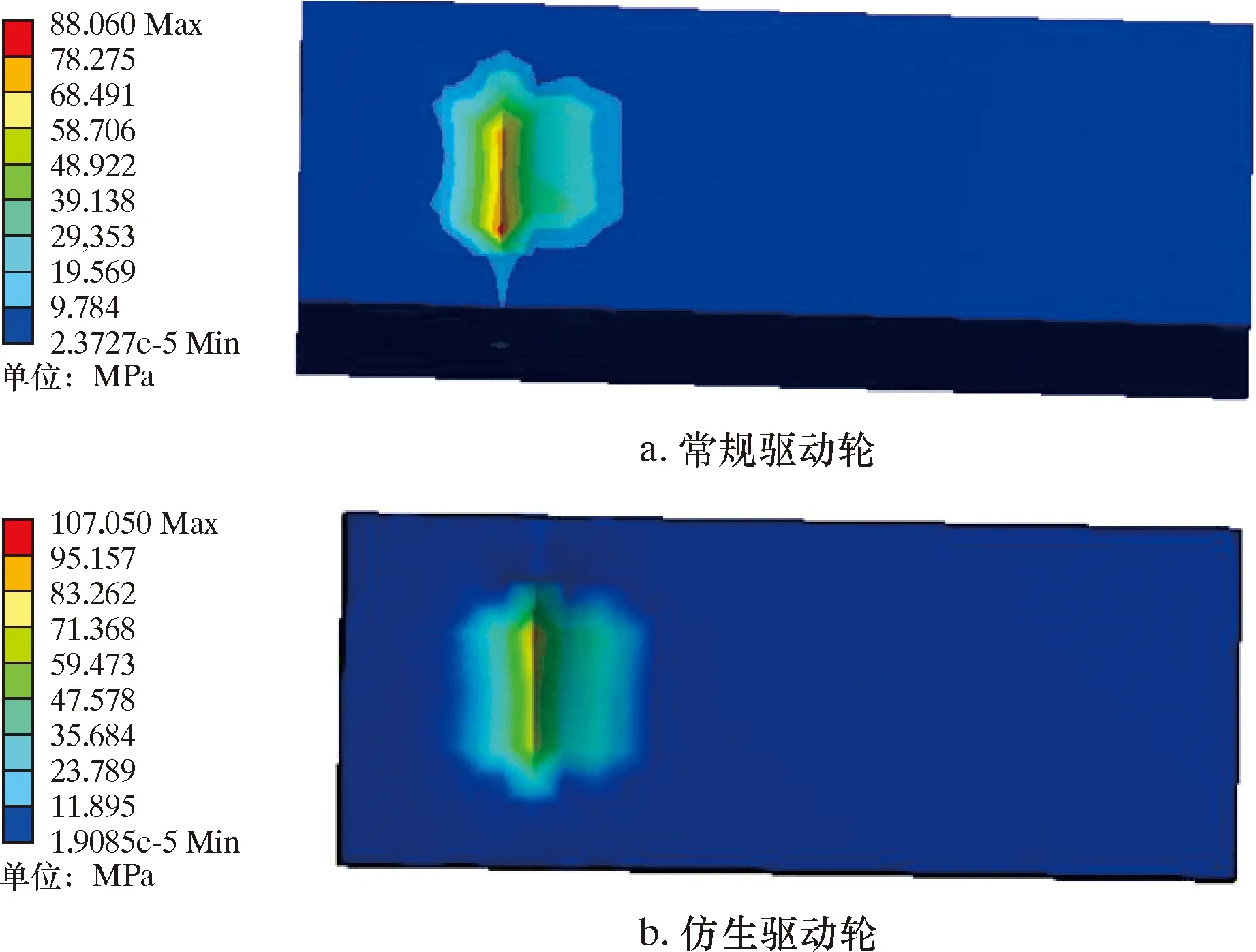
图16 同压时等效应力云图Fig.16 Cloud chart for equivalent stress at the same pressure
从图16可知,常规驱动轮和仿生驱动轮在相同正压条件下爬行时,管壁的最大应力分别为88.06和107.05 MPa。根据表1,在不超过套管屈服强度840 MPa条件下,上述2种驱动轮均不会对套管表面造成破坏,且不会影响套管的后续使用。

图17 同压时位移云图Fig.17 Cloud chart for displacement at the same pressure
从图17可知,常规驱动轮和仿生驱动轮在相同正压力条件下爬行时,管壁的最大变形量分别为0.001 892 4和0.002 448 3 mm。比较可知,同条件下仿生驱动轮比常规驱动轮更易产生犁沟效应,因此更容易获得较大的牵引力。
4 结 论
(1)根据生物耦合特性,提出3种具有一定耐磨性能的生物耦元结构。通过分析计算确定了柱体结构在同种条件下犁沟摩擦因数最优;并将其应用到驱动轮顶面,设计了一种牵引能力更强、脱黏减附效果优良的抗损耐磨仿生耦合驱动轮。
(2)当仿生耦合驱动轮楔入深度为0.2 mm,传统驱动轮齿宽系数λ=0时,仿生耦合驱动轮相比传统驱动轮的牵引能力提高了89%,牵引性能显著提高。
(3)利用有限元仿真软件建立了传统和仿生驱动轮的轮壁接触模型,通过对比同压条件下两者的等效应力与位移云图,得到仿生驱动轮不会对套管造成破坏,且相比传统驱动轮更易获得较大牵引力的结论。
