Spatio-Temporal Cellular Network Traffic Prediction Using Multi-Task Deep Learning for AI-Enabled 6G

Xiaochuan Sun, Biao Wei, Jiahui Gao, Difei Cao, Zhigang Li, Yingqi Li

Abstract: Spatio-temporal cellular network traffic prediction at wide-area level plays an important role in resource reconfiguration, traffic scheduling and intrusion detection, thus potentially supporting connected intelligence of the sixth generation of mobile communications technology (6G). However, the existing studies just focus on the spatio-temporal modeling of traffic data of single network service, such as short message, call, or Internet. It is not conducive to accurate prediction of traffic data, characterised by diverse network service, spatio-temporality and supersize volume. To address this issue, a novel multi-task deep learning framework is developed for citywide cellular network traffic prediction. Functionally, this framework mainly consists of a dual modular feature sharing layer and a multi-task learning layer (DMFS-MT). The former aims at mining long-term spatio-temporal dependencies and local spatio-temporal fluctuation trends in data, respectively, via a new combination of convolutional gated recurrent unit (ConvGRU) and 3-dimensional convolutional neural network (3D-CNN). For the latter, each task is performed for predicting service-specific traffic data based on a fully connected network. On the real-world Telecom Italia dataset, simulation results demonstrate the effectiveness of our proposal through prediction performance measure, spatial pattern comparison and statistical distribution verification.

Keywords: the sixth generation of mobile communications technology (6G); cellular network traffic; multi-task deep learning; spatio-temporality

1 Introduction

The sixth generation of mobile communications technology (6G) is conceived to be the emerging vision of “smart connectivity”, “deep connectivity”, “holographic connectivity” and “ubiquitous connectivity ” [1, 2]. Under this vision, it is expected to offer higher levels of the fifth generation of mobile communications technology (5G)feature extensions such as Tera bits per second(Tbps)-level data rates, sub-millisecond latency,centimeter-level positioning, and ultra-high connection density [3]. Among the technologies toward artificial intelligence (AI)-empowered 6G,mobile cellular traffic prediction, especially in spatio-temporal pattern of the metropolitan level,plays a key role in the global automation of network management, such as online resource reconfiguration, traffic scheduling and intrusion detection. Nevertheless, it is rather an intractable task, due to diverse network demand of mobile applications, frequent spatial transformations and some external factors, e.g., population, holiday,emergency, and social activities.

Currently, deep learning has become the mainstream of spatio-temporal prediction of citywide cellular network traffic. It is able to not only learn potential temporal features in data,but also extract spatial features. For example, C.Zhang et al. proposed a spatio-temporal prediction architecture based on densely connected convolutional neural networks for citywide traffic prediction by treating traffic data as images [4].Furthermore, they combined spatial-temporal cross-domain neural network and transfer learning for large-scale cellular traffic data [5]. K. He et al. designed a deep learning-based graph attention spatio-temporal network for mobile traffic prediction, considering local geographic dependencies and distant inter-regional relationships simultaneously [6]. Q. Zeng et al. proposed an attention-based multicomponent spatio-temporal cross-domain neural network model for 5G/beyond 5G (B5G) cellular network traffic prediction [7]. In this proposal, the convolutional long short-term memory (ConvLSTM) or convolutional gated recurrent unit (ConvGRU) could extract the features of neighborhood data, daily cycle data, and weekly cycle data, and then assigned the weights to these different types of features by attention layer. N. Zhao et al. proposed a spatio-temporal convolutional network for city-wide mobile traffic prediction by introducing an attentional mechanism [8], where the combinations of hourly, daily and weekly traffic were considered. K. Zhang et al. proposed a spatio-temporal graph convolutional gated recurrent unit model for accurate prediction of mobile network traffic, considering the integration of graph convolutional network and gated recurrent unit[9]. However, this wide-area network traffic is usually yielded from multiple type of network service, and the above studies only consider the service-specific single traffic data prediction.Multi-task learning can process different types of tasks simultaneously, reducing computation and storage requirements. Moreover, during the learning process, this mode can make full use of potential knowledge in these tasks for overfitting mitigation and generalization improvement. C.Huang et al. proposed a multi-task learning architecture based on a deep learning model,which used the maximum, minimum, and average values of cellular network traffic as three different tasks to extract features from the traffic data simultaneously [10]. However, the above work essentially divides the same type of data into three related tasks, which cannot make good use of the correlation among the data, and the related tasks are not very helpful. Inspired by this, this paper intends to explore the feasibility of multi-task learning in the modeling of spatiotemporal cellular network traffic, from the perspective of correlations among multiple service data.

On the other hand, the ConvGRU has been proven to be a powerful method in spatio-temporal prediction of cellular network traffic. Compared to ConvLSTM, ConvGRU only transmits information through hidden states instead of cell states, and it has fewer tensor operations and faster model convergence due to only two gate structures. However, ConvGRU only captures spatial information at the current moment, and cannot learn past spatial features at the same time. 3-dimensional convolutional neural network (3D-CNN) focuses on the extraction of local spatiotemporal features. It can pay more attentions to local fluctuation trends, and can extract the temporal dependence of spatial information. Given these, we would like to combine ConvGRU and 3D-CNN to construct a powerful spatio-temporal feature extractor for superior wide-area network traffic prediction.

In this paper, we propose a novel multi-task deep learning framework for citywide spatio-temporal cellular network traffic. In structure, our proposal is a consistent continuous prediction system with the functional parts of the dual modular feature sharing and the multi-task nonlinear approximation (DMFS-MT). The former is responsible for capturing spatio-temporal features effectively. On the basis of these mined useful knowledge, the latter can achieve a favourable prediction in the fully-connected network enabled multi-task pattern. On the real-world Telecom Italia dataset, experimental results show that our DMFS-MT significantly outperforms the state of the arts.

1) This paper is the first to consider multitask learning for simultaneously modeling cellular network traffic of different service types. The correlation among different types of cellular traffic data is demonstrated by Pearson correlation coefficients, supporting our motivation.

2) The dual feature extractor is built newly based on ConvGRU and 3D-CNN for effective spatio-temporal feature extraction. It provides excellent initial points for the subsequent multitask learning.

3) We use the typical fully-connected network as the learner for each task. Specially, the weight scaling coefficient is used to determine the importance of the role that each task plays in the overall training process.

4) The validity of our DMFS-MT is verified experimentally in terms of statistical distribution,spatial distribution and multiple evaluation metrics, compared with popular deep learning models.

The rest of this paper is organized as follows.Section 2 describes the information in the dataset and analyzes in detail the task correlation among the data. The overall structure of the proposed model is given in section 3, and the components of the model are presented separately. Section 4 demonstrates the validity of the proposed model through various experiments. Finally, we review the work done in this paper and give an outlook on future research directions.

2 Preliminary

2.1 Dataset Description

The cellular network dataset used in this paper comes from an open source dataset published in 2015 by a large European telecom service provider, Telecom Italia. Its specific information is shown in Tab. 1. This dataset is one of the most comprehensive spatiotemporal ones, and has been considered in a great many studies [5, 8,11]. Fig. 1 shows the distribution of radio base stations in Milan city and the corresponding structured grid. Here, the city region is divided into 100×100 grids called cells in this paper.Each cell has its own unique ID, as shown in Fig.1(b), and the cell size is 235 m × 235 m, including three main types of services: short message service (SMS), Call, and Internet. Specially, the traffic volume in each cell is denoted by call detail records (CDRs), namely the number of the events on certain service. For a given service, the spatio-temporal sequence of cellular network traffic within Milan city can be expressed as a tensorS={St|t=1,2,...,T},S ∈RT×K×U, whereKandUare the maximum indexes of cells,Tdenotes the maximum time step of the network traffic time series, andStis the global cellular network traffic at thet-th moment, given by

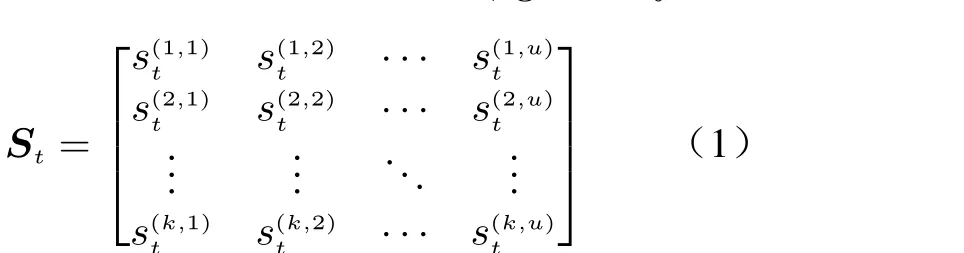
In this formula,k ∈[1,K],u ∈[1,U], and each element denotes the CDRs in the corresponding cell.

Tab. 1 Telecom Italia dataset description

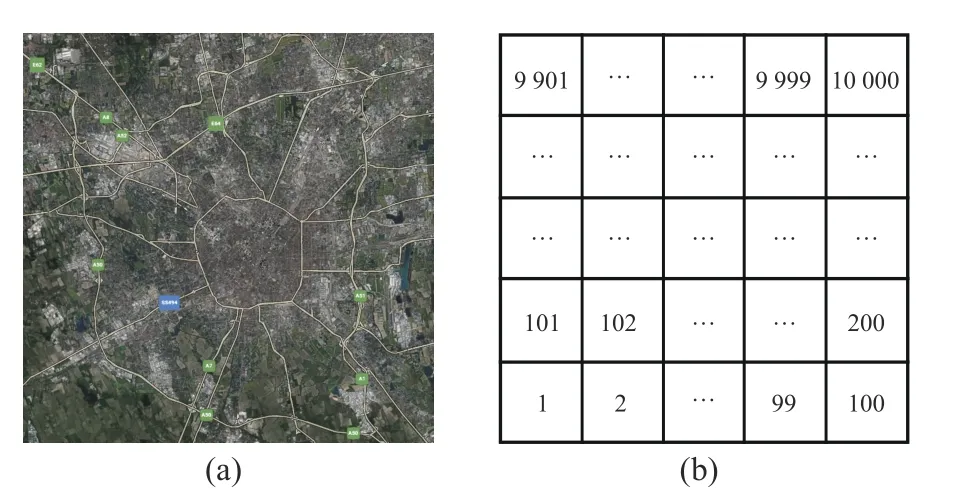
Fig. 1 Milan city and grid map: (a) Milan city map; (b)Milan city grid system

2.2 Problem Statement

To illustrate the motivation of this paper, we first conduct a correlation analysis on the traffic data of three service types, considering six randomly selected cells, based on the following Pearson correlation measure

wheres(k,u) ands′(k,u) denote the data of different service types in the cell (k,u), cov(x,y) is the covariance operator, andσis the standard deviation. The results are listed in Tab. 2. Obviously, there are strong correlations among these three service types of traffic data in considered cells. Generally speaking, the correlation among data can provide highly beneficial prior knowledge supporting for accuracy prediction in theory. Multi-task learning can share relevant features among multiple tasks, and utilize the correlation among tasks to improve the generalization ability of the model. Inspired by it, we would like to explore the spatiotemporal prediction problem of cellular network traffic in the multi-task learning framework, fully considering the correlations among the SMS, Call and Internet data for superior prediction of wide-area cellular traffic.

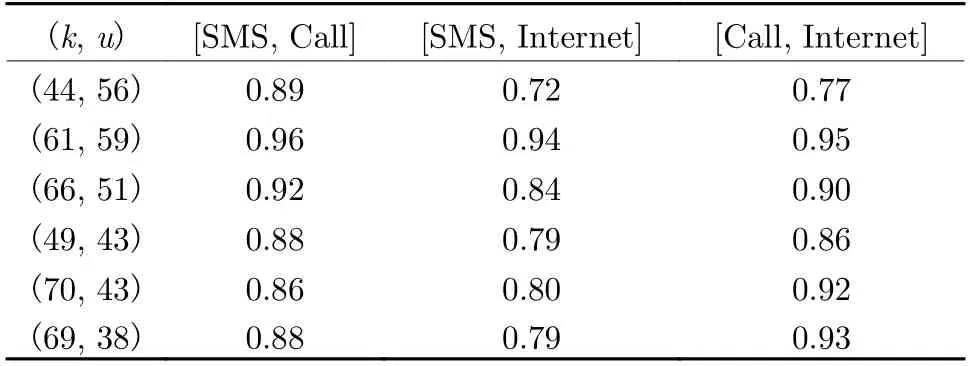
Tab. 2 Correlation analysis of three service types

3 Methodology

In this section, a multi-task deep feature extraction model for cellular network traffic prediction is presented. First, we give the general structure of the model. Second, the components of the system framework are described in detail, including the modules in the shared layer and the separate task-specific layer. Finally, the overall training process of the model is given.

3.1 Overview

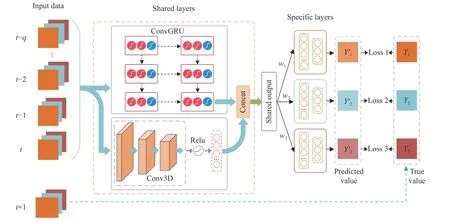
Fig. 2 Multi-task deep learning framework for spatio-temporal cellular network traffic prediction

Such multi-task learning is a classical hard parameter sharing mode, which can reduce the risk of model overfitting by sharing the parameters of the underlying layer and enable each task to learn its own parameters at a specific layer.To utilize the correlation among the traffic data for improving prediction accuracy, a novel multitask learning framework is developed for spatiotemporal cellular network traffic modeling, i.e.,DMFS-MT. Fig. 2 shows a sketch of the DMFSMT framework. Obviously, in structure this framework consists with the following main modules, including data input, newly-built shared layer, specific layer and predicted output. In shared layer, ConvGRU and 3D-CNN are concatenated for extracting the long-term spatiotemporal dependence and local fluctuation trends of cellular network traffic simultaneously. The specific layer, on the other hand, has its own specific parameters for each prediction task. In theory, such construction is able to enhance the effectiveness of model prediction. Subsequently,these two functional modules are described in detail.

3.2 Dual-Module Feature Sharing

Our dual-module feature sharing is achieved via the combination of features extracted by ConvGRU and 3D-CNN in the shared layer. For the convenience of the following discussions, the global cellular network traffic at thet-th moment is defined asXt={Stα,Stβ,Stγ}containing the traffic data of the SMS, Call and Internet services, and each input sample is denoted asI={Xt-q,...,Xt-2,Xt-1,Xt}. Obviously, our input data flow is produced by means of a timesliding window with the window size ofq. Given these, the feature extractions of ConvGRU and 3D-CNN are stated as follows.

Firstly, the ConvGRU module is to extract the spatio-temporal features of cellular network traffic. This module uses convolutional kernels instead of fully connected layers in gated recurrent unit (GRU), which greatly reduces the number of parameters and enables the extraction of more complex features, thus being suitable for spatio-temporal sequence modeling. In fact, ConvGRU removes the memory unit from the ConvLSTM model and selectively retains useful information through two self-parameterizing control gates, namely, the reset gate and the update gate. It endows the model with an ability to effectively capture spatiotemporal trends.Specifically, a ConvGRU unit can be formulated as

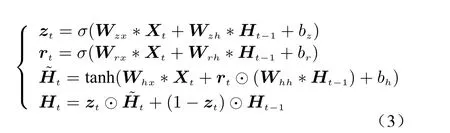
whereXtandHtare the input and output of the network at the timet, respectively,ztandrtdenote the output of update and reset gates,Wandbare the weight and bias of the corresponding gate and layer in the network, * and⊙denote the convolution operation and Hadamard product,z,x,r,hdenote the indicators of update gate, input layer, reset gate and hidden layer,respectively.

On the other hand, a 3D-CNN extractor,extended from the standard 2-dimensional convolutional neural network (2D-CNN) model with a temporal dimension, is designed in the sharing layer as the supplement of the ConvGRU-based feature extraction. This is because ConvGRU can only capture spatial information at current moment, but ignoring past spatial information,while 3D-CNN is more attentive to local fluctuation trends, and can extract the temporal dependence of spatial information. In our consideration, the newly-built 3D-CNN is composed of 3D convolutions, activation functions and fully connected layers. First, the local spatio-temporal features extracted from the cellular network traffic data after convolutional operations and activation are represented as

whereVis the output of the convolution operation,fis the relu activation function, andWcandbcrepresent the weights and biases of the fully connected layer, respectively. Moreover, we concatenate the outputHof ConvGRU and the outputCof 3D-CNN in the feature dimension to get the final outputOof the shared layer.

3.3 Task-Specific Layer

In task-specific layer, the parameters unique to each task is learnt via the fully connected network, so that the spatio-temporal features of each task can be extracted. It is beneficial to yield more semantic information. In our consideration, the weight scaling coefficients are designed to determine the importance of each task, and they are trained along with the original parameters of the model. Based on this, the output of our multi-task prediction model is given by

whereθ1,θ2andθ3represent the global training parameters of the three tasks, respectively,including the weight scaling coefficients of each task (w1,w2,w3), the weights and biases in the fully connected layer (T1,T2,T3,b1,b2,b3), and the weights and biases corresponding to the two modules in the shared layer, andδ1,δ2andδ3denote the mean absolute errors of the predicted and true values of the three tasks, respectively,expressed as

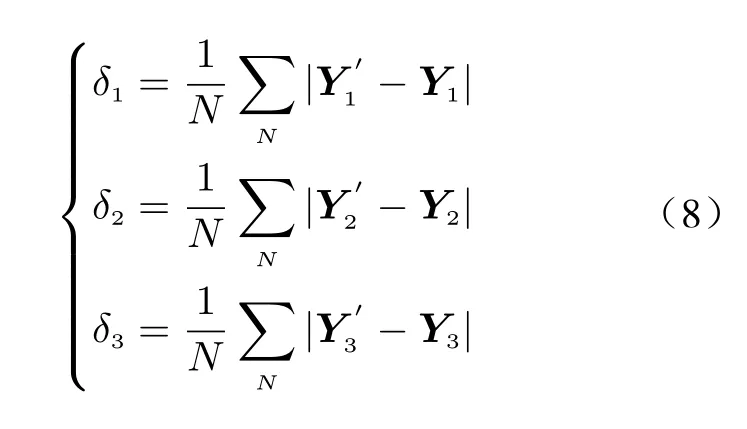
whereNrepresents the number of samples,Y1,Y2andY3represent the real values of the three tasks, respectively. Obviously, the DMFS-MT training is actually a global process, which not only trains the parameters unique to each task,but also fine-tunes the parameters in the shared layers.

3.4 Training Process

Algorithm 1 gives the pseudo-code for the DMFS-MT training. The model initialization contains the definition of loss thresholds, the construction of multi-service data series, data preprocessing based on normalized methods, and the dataset division (Lines 1－3). During the training process, the main purpose of model training is to determine the optimal parametersθ1,θ2, andθ3in the shared and the task-specific layers. Specially, the output of the shared layer is obtained by concatenating the output of ConvGRU and 3D-CNN in the feature dimension, and then the output of the task-specific layer is obtained by(6) (Lines 6－16). After the DMFS-MT training is achieved, its generalization performance is further verified over the testing operation (Lines 18－22). Once the total test loss is less than the thresholdβ, the generalization performance of our model is optimal, proving the effectiveness of the trained DMFS-MT (Lines 23－25).

Algorithm 1 DMFS-MT training Input: Multi-service data sequence: X ={Xt|t=1,2,...,T};

loss threshold β.Output: Learned DMFS-MT model, three task test outputs: , , .DN ={In|n=1,2,...,N}ˆy1 ˆy2 ˆy3 1: Construct X as a dataset: ;2: Standardized datasets using (9);DN Dtrain Dtest 3: Divide the datasets into and ;i=1 4: for to epochs do 5: # Training 6: for d, y in do 7: # Shared layers Dtrain p1←8: ConvGRU module output (3);p2←9: 3D-CNN module output (4);10: concat ;11: # Specific layers←12: {o1, o2, o3} {p3 × w1, p3 × w2, p3 × w3};←13: Three task outputs: r1, r2, r3 (6);←14: Model training loss L (7);θ1,θ2,θ3 15: Update according to the loss L;16: end for 17: # Testing p3 = (p1,p2)18: for d, y in do ˆy1 ˆy2 ˆy3 =Dtest 19: , , model (d); # Test model with optimal parameters Ltest←20: Model testing loss (7);Lsum =Lsum+Ltest 21: ; #Lsum is the cumulative loss 22: end for Lsum ＜β 23: if then 24: Save model and prediction data;25: end if 26: end for

4 Experiments

In the following experiments, we give a comprehensive evaluation of the prediction performance of the proposed DMFS-MT model for cellular traffic prediction. The extremely challenging dataset from Telecom Italia in 2015 is considered,including SMS, Call and Internet, and its details have been depicted in Section 2. To verify the advantages of our proposal, we also evaluate some state-of-the-arts, including long short-term memory network (LSTM) [12], 3D-CNN [13],ConvLSTM [14], ConvGRU [15] and ConvGRUMT. Specifically, ConvGRU-MT is a multi-task learning version of ConvGRU. Firstly, the data pre-processing method and the setting of model parameters are described, respectively. Then the four quantitative metrics are given for the performance measure of the evaluated models. Finally,the effectiveness of the DMFS-MT model is demonstrated via training loss measure, global prediction performance, and local performance verifications on the trend, spatial pattern and statistical distribution of the predicted traffic in certain cell.

4.1 Data Pre-Processing and Parameter Setting

As discussed in [5], the quality of the used Italia Telecom dataset can directly affect modeling utility of cellular traffic. Given this, our data preprocessing is mainly to handle values, where the standard method can achieve the filling of missing data point by averaging its surrounding ones[16]. In addition, in order to obtain the same magnitude data, the z-score normalization method is considered to scale all network traffic data to a specific interval, defined by

wheredandxdenote the original and processed data, respectively,d¯ andσrepresent the mean and standard deviations of the original data,respectively. It should be specially explained that the inverse normalization is performed for obtaining true training and testing results. As is analyzed from Italia Telecom dataset, there is a large amount of unrecorded traffic on the 10-minute time scale, which is not conducive to the prediction of cellular network traffic. To tackle this issue, the time granularity of this dataset is rescaled to 1 h, and all data within each hour are accumulated to obtain a new data record.

In our experiments 1 485 pieces of data are considered, of which 75% are training data and 25% are testing data. The input time window of these models is set to be 3, and that is, the current data and their adjacent past two data are used to predict the one at the next time. All simulation results are obtained after averaging five experiments. Tab. 3 lists the parameter setting of all evaluated models for our cellular network traffic prediction. These experimental parameters are determined by the popular grid search method.Besides, the Adam optimizer is adopted to speed up the training process of models by alleviating gradient oscillation.

Tab. 3 Model parameter configuration

4.2 Performance Metrics

In order to comprehensively evaluate the effectiveness of the proposed model in our scenario of multi-task prediction, three metrics are considered here for accuracy measure, including normalised root mean square error (NRMSE), mean absolute error (MAE) and R-squared (R2), given by

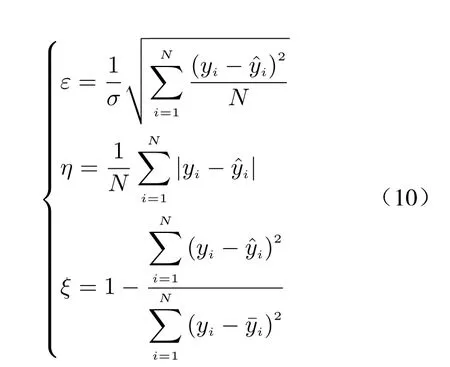
whereε,η, andξdenote NRMSE, MAE, and R2,respectively,yiandyˆidenote the true and predicted values of a single sample, andσis the standard deviation of the test data.

Generally, the smaller the value of MAE and NRMSE is, the smaller the residuals of the prediction results will be, meaning better prediction performance. R2∈(0,1) reflects the performance of the model in capturing the variability of the target time series, i.e., the goodness of fit, and the closer its value is to 1, the more powerful the model is in predicting the variability of time series data. Additionally, the model efficiencyrcan measure how long the loss is not changing,given by

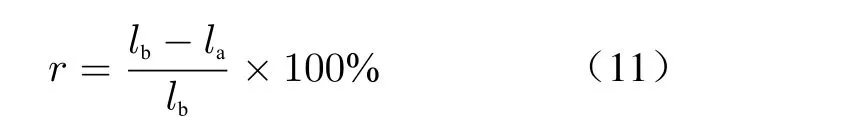
wherelaandlbdenote the loss of the current and previous epoches, respectively.

4.3 Global Performance Evaluation

Fig. 3 shows the degree of loss dropping in each epoch during the DMFS-MT training in our multi-task learning of cellular network traffic,including the model MAE and the rate of loss dropping (see (11)) for each iteration. From two subfigures, we observe that these two training indicators become stable after 10 iterations,implying that our model can achieve an effective convergence of training state. Fig. 4 shows the performance comparison of all evaluated models in the prediction tasks of SMS, Call and Internet traffic. Obviously, our DMFS-MT model signific antly outperforms the considered alternatives,being capable of obtaining more satisfactory NRMSE, MAE and R2. We intend to give two key comments. The first is that such a superior DMFS-MT is attributed to the newly added dual-module feature sharing, which can capture the spatio-temporal dependency among traffic data more effectively. Our second comment regards the multi-task learning. As we notice,DMFS-MT and ConvGRU-MT are superior to these non-multitask learning models in prediction performance, since this learning mode can make full use of close correlations among SMS,Call and Internet traffic. Besides, we also note that the LSTM model, empowered with good temporal modeling rather than spatial one, has the worst prediction performance.

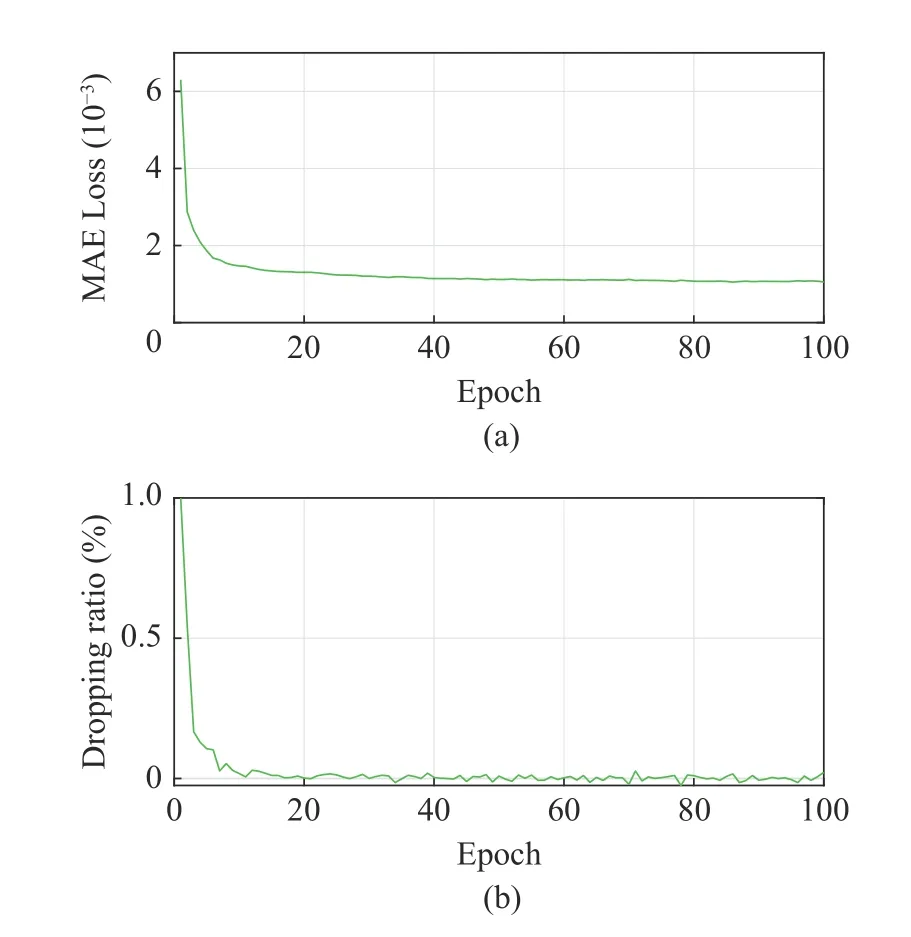
Fig. 3 DMFS-MT training evaluation: (a) training loss; (b)dropping ratio

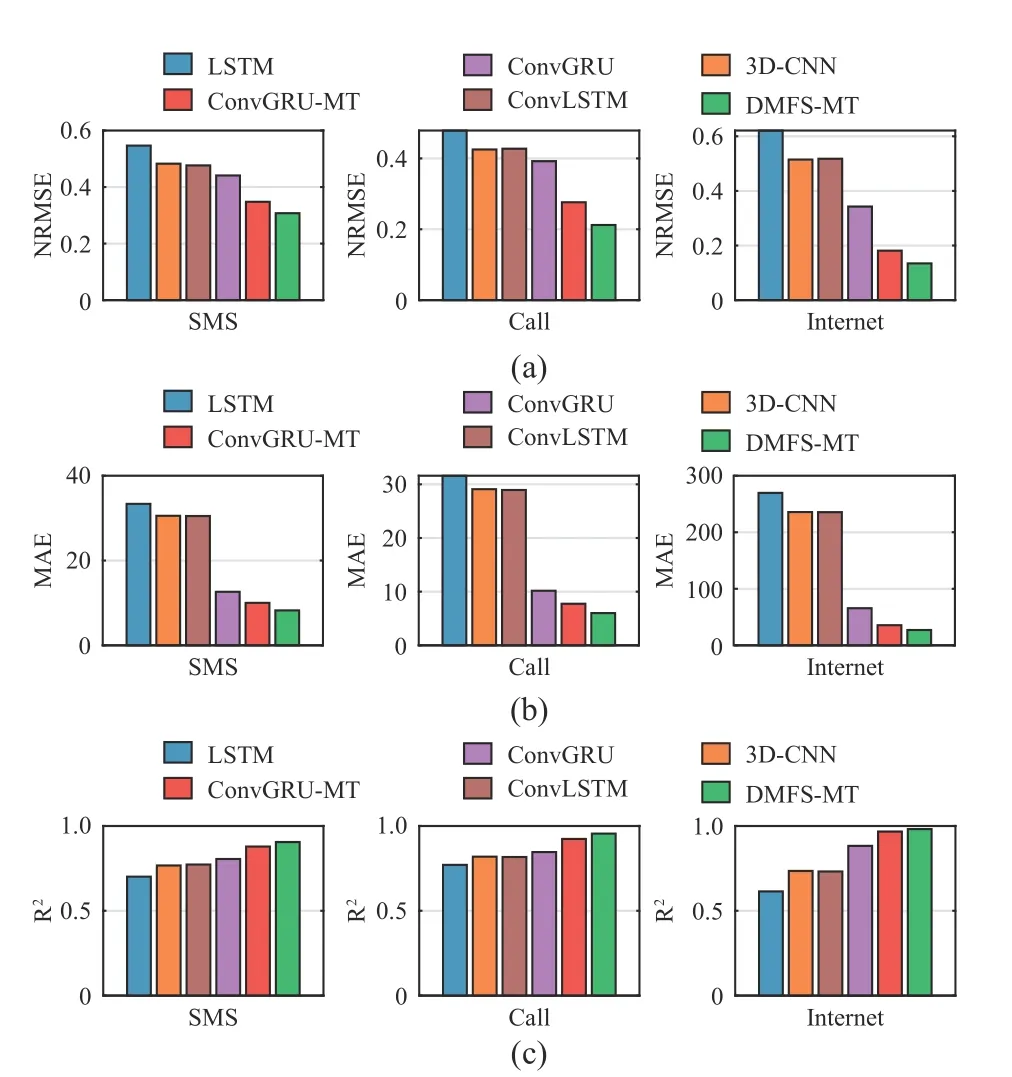
Fig. 4 Performance comparison of all models in multiple evaluation metrics: (a) NRMSE; (b) MAE; (c) R2

4.4 Cell-Level Performance Verification

To further verify the effectiveness of our proposal, the cell-level evaluation is considered for the trend, statistical distribution and spatial pattern of traffic data, concentrating on traffic prediction performance of certain cell over the whole time regions or all cells at a certain moment.Fig. 5 shows the predicted results for LSTM, 3DCNN, ConvLSTM, ConvGRU and ConvGRUMT within the entire testing time region, where a cell (44, 60) is randomly selected for experimental comparisons. From this figure, we can intuitively see that the proposed DMFS-MT has the strongest nonlinear fitting capacity of real cellular network traffic data, while the other models behave badly, because their predicted values deviate significantly from real ones at peak or through moments. On the other hand, we also observe that these evaluated models have relatively poorer prediction performance for Internet data compared with SMS and Call in this cell. It is due to the fact that the Internet traffic is generally characterised by remarkable random, chaos and burstiness, due to the random and chaotic characteristics of this data, but the SMS and Call traffics are yielded from more regular activities of people, facilitating the learnability of spatio-temporal correlation. Furthermore, from the perspective of statistical analysis we show the violin plots of the predicted SMS, Call and Internet traffic in the cell (44, 60) for all evaluated models, as shown in Fig. 6. Each violin plot is composed of a box plot and density traces situated to its left and right. The symmetric density traces can visualize the distribution of the predicted traffic data, and its width reflects the frequency of occurrence of data points. The built-in boxplot gives the basic distribution information of data, such as quantile, medians, etc. Observing the shape of violin plot, as well as quantile and median, we can find that the statistical distribution of different service traffic data obtained from DMFS-MT is closer to the actual one, suggesting its optimal prediction.

Fig. 5 Comparison curves of true signal and predicted results of the evaluation models on the cellular network traffic of randomly selected cell (44, 60): (a) SMS; (b) Call;(c) Internet

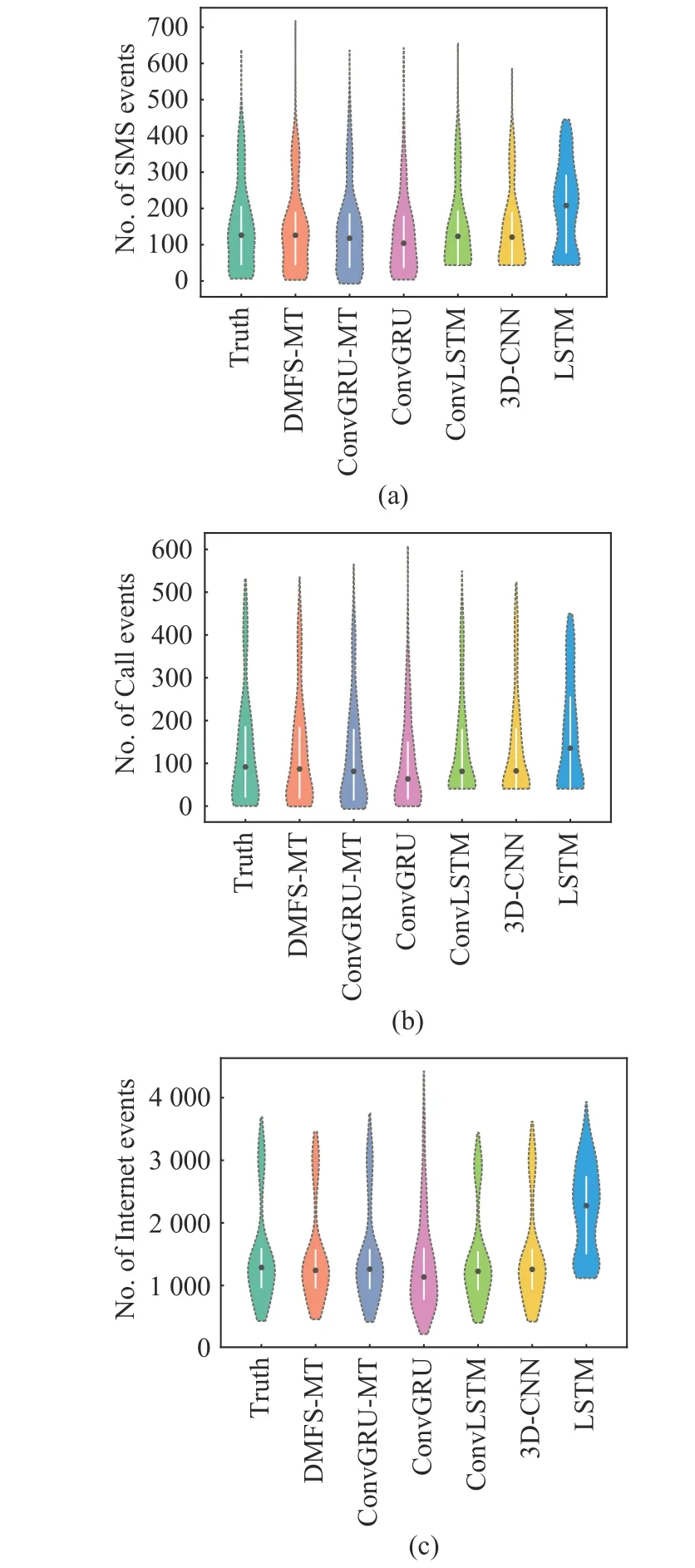
Fig. 6 Violin plots of the true and predicted traffic data of randomly selected cell (44, 60): (a) SMS; (b) Call; (c)Internet

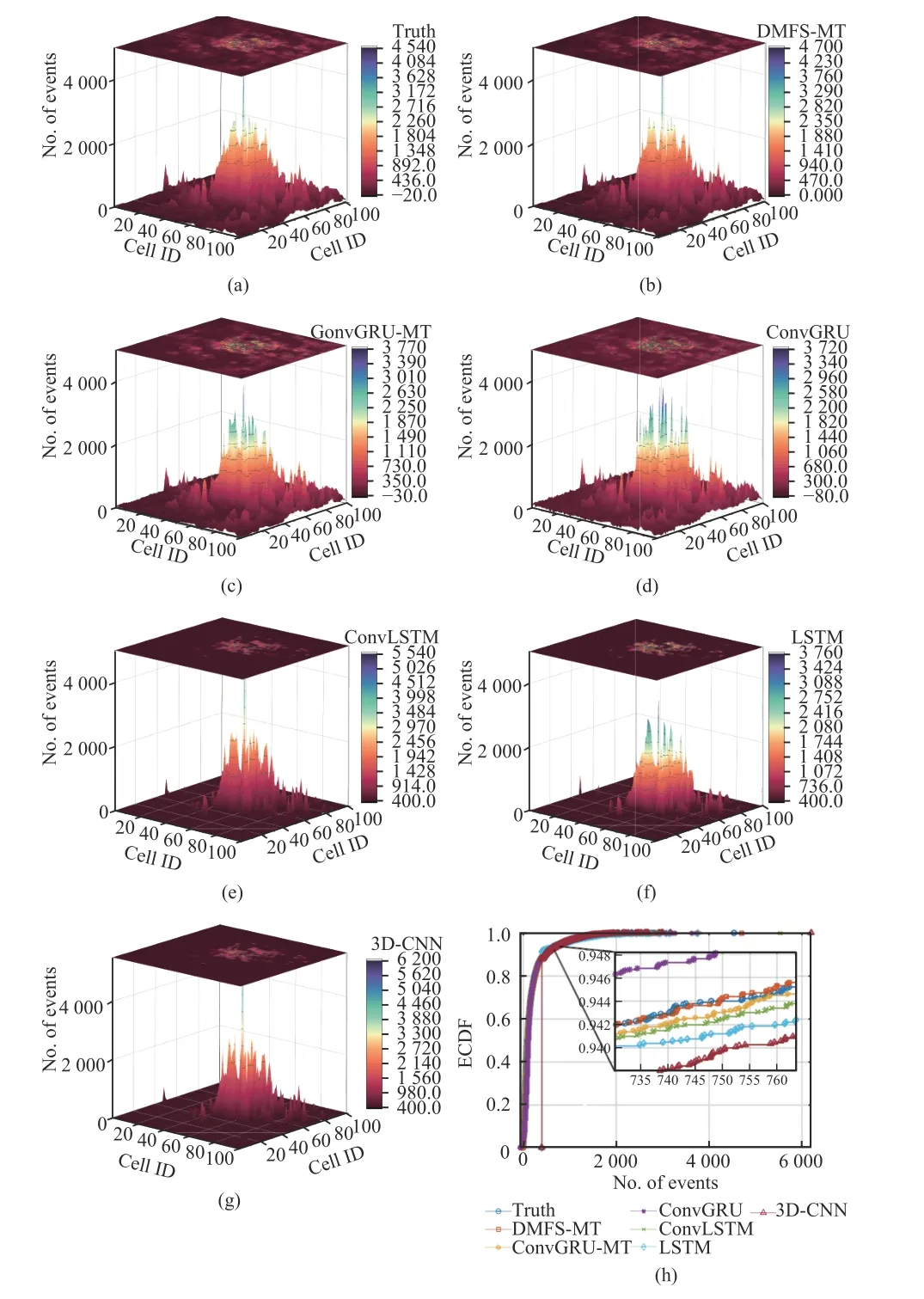
Fig. 7 Spatial distribution and ECDF plots of the true and predicted traffic data: (a) truth; (b) DMFS-MT; (c)ConvGRU-MT; (d) ConvGRU; (e) ConvLSTM; (f)LSTM; (g) 3D-CNN; (h) ECDF

Finally, Fig. 7 shows the snapshot and empirical cumulative distribution function(ECDF) of predicted traffic data from all cells at a certain moment. Here, each snapshot not only visualizes the spatial distribution of cellular network traffic, but also distinguishes the intensity of the number of occurred Internet events via the heat map at the top. As expected, DMFS-MT is able to produce the spatial distribution of traffic data most consistent with the real one among these models, indicating the best data modelling capacity, followed by ConvGRU-MT and ConvGRU. Nevertheless, LSTM is still the worst performing model, since there exit massive zerovalue and unmatched peak points. And we statistically measure the traffic in all cells at a certain moment to get the ECDF graph. Again, the prediction results of the proposed DMFS-MT are still the closest to the true distribution and superior to the prediction performance of other models.

5 Conclusion

In this work, we investigate a multi-task prediction framework based on deep feature extraction for spatio-temporal prediction of cellular network traffic. We also analyze the Telecom Italia dataset to explore the feasibility of modeling multiple business data simultaneously under wide-area traffic. Based on these observations, a novel dual-module feature-sharing multi-task network traffic prediction model is proposed. Specifically, Combining ConvGRU and 3D-CNN, a multi-task shared layer for extracting different spatiotemporal features is constructed. In addition, we also set three weight scale coefficients to determine the importance of each task in the task-specific layer. And task-specific layers with different parameters are constructed through fully connected layers. Simulation results show that our proposed DMFS-MT significantly outperforms other models on real cellular network traffic data compared with existing efficient deep models, proving that the model has great potential in cellular network traffic prediction.

A possible extension of this work is to explore other types of multi-task learning modalities for mining correlations among multiple data types. In addition, finding a more effective spatiotemporal feature extraction module will be an important direction worth exploring in the future.