Optimize the Deployment and Integration for Multicast-Oriented Virtual Network Function Tree

Ying Chang, Hongxue Yang, Qinghua Zhu

Abstract: Due to the development of network technology, the number of users is increasing rapidly,and the demand for emerging multicast services is becoming more and more abundant, traffic data is increasing day by day, network nodes are becoming denser, network topology is becoming more complex, and operators’ equipment operation and maintenance costs are increasing. Network functions virtualization multicast issues include building a traffic forwarding topology, deploying the required functions, and directing traffic. Combining the two is still a problem to be studied in depth at present, and this paper proposes a two-stage solution where the decisions of these two stages are interdependent. Specifically, this paper decouples multicast traffic forwarding and function delivery.The minimum spanning tree of traffic forwarding is constructed by Steiner tree, and the traffic forwarding is realized by Viterbi-algorithm. Use a general topology network to examine network cost and service performance. Simulation results show that this method can reduce overhead and delay and optimize user experience.

Keywords: multicast; service function chain (SFC); network functions virtualization (NFV); software defined network (SDN); Viterbi-algorithm

1 Introduction

In the future, the 6G wireless network will be characterized by node densification, intelligentization of terminals, diversification of functions[1], such as integration of heaven and earth communication [2]. These characteristics have prompted operators to lower their hardware input. The appearance of network functions virtualization(NFV) has provided a solution to the aforesaid problem. According to the NFV technology [3], it is virtualized to decouple specific functions of hardware with specific functions, and deploy the network functions on the universal server. This can significantly reduce the hardware input and maintenance cost, thus accelerating the function development efficiency. Additionally, to realize flexible control of traffic data, software defined network (SDN) has been applied to the service function chain (SFC) [4]. With the rapid development of the SDN/NFV technology, the SFC technology has gradually emerged as a popular service mode. Logically, the SFC connect network services into a set of orderly services. The traffic data pass by the corresponding service device in accordance with the path information in the message. It even plays an important role in network security [5].

Usually, a data flow needs to flow through a series of network functions to reach the destination, that is, the SFC. The emergence of NFV reduces the cost of the embedded solution of SFC and makes the choice of deployment location more flexible. NFV transforms specialized hardware devices into virtual network functions that run on general-purpose servers in the form of virtual machines, containers, or processes. NFV can effectively improve the flexibility of service function chain deployment and management, and reduce maintenance operations. The birth of SDN technology has further leveraged the advantages of SFC technology. The resource allocation of SFC based on virtualized infrastructure is not simple, and it mainly includes three stages：VNF chain composition, VNF forwarding graph embedding and VNF scheduling. Because of the diversified placement modes of SFC middleware,the network has been faced with problems, such as traffic rotation and path complication. So,finding an optimal layout has been a tricky issue.It is of vital significance for scholars to study optimized placement of the service chain and design of an optimized middleware placement plan.

The VNF nodes and chain mapping process in the SFC are corresponding to the nodes and chain mapping process of the traditional virtual network embedding (VNE) [6]. Special note is that VNE prior presents a virtual network topography, while the service function chain embedding (SFCE) does not provide a fixed topography. Optimization of VNF has been proved to be NP-hard, and many scholars have proposed efficient heuristic and metaheuristic approaches [7].But to solve the optimal layout overhead has been an NP-hard issue. So, this paper proposes a universal algorithm that can bring down the overall expenditure.

So far, multiple heuristic SFCE methods have been proposed in [8−10]. In [11], an adaptative multicast clustering technology is developed,which minimizes the resources required for the establishment of the sense-based SFC. In [12], an availability-sensed SFC mapping is put forward to minimize the consumption of physical resources, and provide high availability for the future service request within the polynomial time. In [13], a cost-saving algorithm based on reliability is introduced to minimize the embedding cost required to balance the capital expenditure and the operation expenditure of the telecommunication service provider [14]. In [15], a dynamic service is in connection with the existing study’s method, which dynamically generates a service chain through reinforcement learning. In [16], it models the embedding problem as a Markov decision process, in which the reward is modeled as an adjustable weighted function,including combined delay (wired and wireless delay) and remaining resource. Accordingly, a lightweight and adjustable Q-learning-based SFC embedding strategy is proposed.

The NFC technology seeks decoupling between network service function and hardware equipment to change the service placement mode of the traditional network. The SDN framework separates the control surface from the data plane to change the network architecture. The combination between NFC and SDN has strengthened the network flexibility and scalability to make resource sharing possible and to provide technological support for the development of SFC. By efficiently improving the network construction efficiency, the SFC technology can cut down the overall operation expenditure. But relevant technologies of this field still have a huge room for improvement. How to integrate the NFV technology, SDN, cloud computing and SFC-related technologies calls for further exploration.

2 Models

2.1 Related Technologies

SFC is a network solution after the integration of NFV, SDN, cloud computing and other technologies. Its main functional components include SFC system management interface, policy controller,flow classifier, hardware equipment, and network middleware, SFC allows network service does not follow linear order, and can change the order without affecting service performance. SFC may also have multiple branches.

Different VNF placement and SFN chain plans can bring about dramatic changes to cost and benefit of the telecommunication service provider. This problem has been defined as an issue of VNF Placement and Traffic Steering(VNFP-TS). Nevertheless, current researchers generally focus on one aspect [17,18]. For example, Refs.[6] and [19] focus on the multi-stage solution for NFV-enabled multicast over the hybrid infrastructure. In this paper, the propagation delay and bandwidth overhead are comprehensively considered to analyze the comprehensive overhead under different VNF placement and traffic steering. In this paper, an efficient model is designed for the mapping from the NFV-based virtual multicast request to the basic network, attempting to reduce the propagation delay and minimize the resources required under the prerequisite of satisfying functional requirements.

2.2 System Model

First, conduct system modeling for the underlying network topography, and the model is an undirected graph, which can be written asG=(N,E), whereNdenotes the set of physical nodes made up of switching nodes,Ns, and functional nodes,Nf;Edenotes the set of physical chains.

Placement of VNF is infeasible to all switching nodes,nNs. Therefore, consumption of capacity is not taken into account. As to functional nodes,nNf, placement of multiple VNFs is viable. The available capacity of computing resources isc(n), so placement of VNFs will consume the computing resources. If the computing resources available are smaller than VNF-occupied resources, VNF placement is considered a failure. Every VNF can cope with multiple SFC requests. Since the delay within the node is extremely short, the consumption of delay is omitted.

In terms of every physical chain,en,m(∈E),n ∈N,m ∈Ωn,Ωnis a set of adjacent nodes of the noden. In order to simplify the model, it is believed that the available bandwidth resources are infinite, but the data traffic, while passing the physical chain, can cause consumption of chain bandwidth resources, whose unit bandwidth overhead is denoted byμ. Communication of data traffic between physical chains is a main factor of delay. The communication delay is denoted byδ(en,m); while the unit delay punishment overhead is represented byϵ.

2.3 Decision-Making Variable

2.4 Objective Function

In this paper, two indexes are used to examine the model performance, end-to-end delay and bandwidth consumption, because these two indexes can represent two optimization perspectives. Specifically, end-to-end delay can reflect the performance of the network application, so users hope to minimize it, but the network supplier attempts to minimize the total bandwidth consumption to reduce the opportunity and operation cost of congestion. When NFV-MP is solved under the minimized cost, the delay overhead is indicated by cost(Ti); while the bandwidth overhead is indicated by cost(Ri). In this paper, these two indexes are combined, and their weighting and combined objective function can be used to denote the comprehensive overhead.cost(Tq) and c ost(Rq) are defined as

2.5 Constraint

2.5.1 Ensuring Placement of All VNFs

2.5.3 Flow Maintenance

To ensure all virtual chains to be deployed and prevent all data traffic from shunting after passing the last VNF, the constraint between the node variable and the chain variable exists.

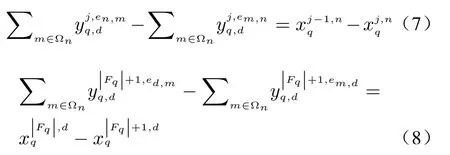
All functional nodes are limited by the computing resource capacity. VNF placement is only viable under the condition of meeting the capacity restriction.

2.5.4 Node Capacity Restriction

2.6 NP-Hard Problem Verification

This part aims at verifying whether the optimal comprehensive overhead of SFC is an NP-hard problem. It can be verified from the perspective of polynomial time reduction of the Steiner Tree Problem. Assume that there is a topological graph,G=(V,E), whereVandErepresent the node set and the chain set, respectively. In terms of every chain, e∈E, its chain overhead isCe.Regarding a subset of a given node set, the Steiner Tree Problem is to find out a minimum cost tree O PTGof all nodes that crossesD.

First of all, an SFT-embedded case is constructed. CopyGtoG′; copyDtoD′. In addition toG′, consider the node setP={p0,p1,...,Pn}. Each chain can generate overhead. Connectdj ∈D′inG′topi ∈P, and endow this side with a random overhead. Besides,p0can be adopted as a source node, and other nodes inPcan be adopted as the server for placement of VNFs. All nodes inG′can only be adopted as intermediate nodes or destination nodes. This paper assumes that some VNFs have already been placed inP; every node inPhas the capacity limitation. Placement of new VNFs inPcan generate costs.

Assume that a multicast task in theG′∪Pisδ=(P=p0,D=D′,l),and that this paper can find the optimal solution, OPTG′, as the SFT embedding. Since all VNFs can be placed onP,this paper can deleteP, and the side betweenPandG′. The remnant subgraph of OPTG′,G′, is the OPTGofG. Otherwise, OPTG′is not the optimal solution plan. This means that this paper can find the optimal solution to the Steiner Tree Problem. However, the Steiner Tree Problem has been proved to be the NH-hard problem [12], so the hypothesis is not verified. The optimal comprehensive overhead of SFC is an NP-hard problem.

3 Algorithm

In this part, a two-stage approximation algorithm is proposed to address the issue of optimal SFT embedding. At the preparation stage of the algorithm, a topographical network is first constructed.

3.1 Network Construction

Algorithm 1 describes the generation process of multiple service chains. First, the objective network is converted into a multistage overlay network containing all information of the primitive network, such as the information of nodes and chains. The USANET model is used to construct the topographical network. The primitive network contains 24 nodes. The weight of each side represents the chain propagation delay. Since nodes are divided into switching nodes and functional nodes, VNF can be placed on functional nodes only, so the capacity of switching nodes is set to be 0. The computing resources capacity of all nodes randomly generated. The computing resources required to randomly generate 8 VNFs and the computing resources required to generate each VNF. Refer to Algorithm 1 for more details.

Step 1 Randomly generate the service chain length, Length, source node position, InNode,and the service chain bandwidth consumption.The first column of the multicast service chain matrix stores the service chain length; the second column stores InNode nodes; the 19th column stores the service chain bandwidth demand.

Step 2 When the VNF number to be placed by the service chain is Length–1, and Column 3–10 of the multicast service chain matrix are used to store the VNF types of storage service chains, placement is not necessary, and the computing resource demand is set to be 0. Therefore,3 – (Length +1) of the multicast service chain matrix stores Length–1 unrepeated VNF types,and the computing resource demand is set to be 0, which means no placement of VNFs is necessary. Column 11 to 18 of the multicast service chain matrix is corresponding to the aforesaid VNF computing resource demand. If VNFs are not placed, the computing resource demand is set to be 0.

Step 3 Rank the service chain in an ascending order by the service chain. If the service chain length is equal, rank the bandwidth consumption by the ascending order, and save the service chain ranking results in Column 19 of the multicast service chain matrix.

Through the aforesaid three steps, a random multicast service chain matrix can be generated. The construction process can ensure the total number of the multicast service chain demand of the multicast service chain, position of the source node, number and position of destination nodes, number and type of VNFs, bandwidth demand and VNF sequence to meet the requirements of VNF placement.

3.2 Two-Stage Algorithm

In this part, a two-stage approximation algorithm is proposed to address the issue of optimal SFT embedding.

3.2.1 Finding Out a Feasible Solution Plan

At this stage, a placement algorithm is set to find out the feasible solution for the issue of optimal embedding of the service function tree(SFT). First, SFC is embedded in the topographical network. Then, the last node of SFC is connected to all destinations. Refer to Algorithm 2 for more details.

Step 1 Read the service chain matrix,acquire the service chain length (Length), source node position (InNode) and so on, and embed InNode into the corresponding nodes of topography as the initial nodes of the service chain.

Step 2 Use the graphshortestpath function from the source node to the destination node(placement of the nodes of the last VNF) in turn to find the shortest path required to find the embedded adjacent VNF. Save the path, bandwidth overhead and delay information.

Step 3 Find a Steiner tree connected to all destination nodes in terms of nodes placed with the last VNF. So, the Steiner tree generated by Step 2 can generate a feasible solution to the issue of SFT embedding. But the solution thus obtained might be the locally optimal solution.The solution thus obtained calls for further verification. If the corresponding problems still exist,adjustments should be made.

3.2.2 Optimizing the Feasible Plan Since some nodes might not have adequate resources for placement of multiple VNFs, it is necessary to check every functional node in sequence. If the last node fails in VNF placement or the current nodes have inadequate capacity, the VNF placement of the current nodes is inadequate. On the contrary, if the nodes have adequate capacity, the shortest overhead is compared repeatedly according to the shortest path. After the placement finishes, the bandwidth use status and the remaining node resources are updated.

After placement of each node is finished, the minimum overhead and corresponding path from the source node to the current node is reserved.When placement of the last VNF is completed,multiple placement paths and corresponding minimum overhead can be obtained to reserve the ultimate outcomes. So, embedding of SFC is completed. At last, the generation of the Steiner tree from the last VNF to the destination node is completed. Generation of the Steiner tree problem will generate the bandwidth overhead only.The overhead for placement of each VNF and the overhead for generation of Steiner tree problem are added up to obtain the final results. Multiple paths are compared to obtain the minimum overhead and reserve the final results. See Algorithm 3.

Algorithm 3 Optimized Deployment Results Input DeployCell OutPut NodeResource, Path, Delay, and the final deployment overhead 1 N is the DeployCell array length.2 for i＝1：N* *3 Cost=α Deplay+β Bandwidth 4 end 5 Cost=min(Cost)

3.2.3 Algorithm Analysis

The time complexity of this algorithm can be written asO(|i|2×|j|2×|ℓ|+|N|), where|i|denotes the number of all nodes, |j| denotes the number of functional nodes, |ℓ| denotes the service chain length, and |N| denotes the Deploy-Cell array length.

4 Experiments

In this part, the algorithm performance verification method is introduced. Following that, the algorithm performance is verified. The verification focuses on quantizing the performance of the algorithm in reducing the chain propagation delay and bandwidth resource overhead.

4.1 Experimental Parameter Setting

In order to verify this algorithm, this paper uses the USANET model to generate a topographical network, which is a 24-node, 43-chain network.As to this network, the influence of the SFC length and number, number of destination nodes,and average resources occupied by each VNF placement is assessed. The generation of the topographical network, generation of node parameters, and generation of VNF parameters are all priori content. The settings can be made in advance according to the experiment needs without occupying the application operation length of time. All the parameters are set as below.

Node parameters: Randomly choose 20% of nodes as switching nodes. Randomly set computing resource capacity of function nodes by the 6 –8 uniform distribution. The switching node computing resource capacity is set to be 0.

Chain parameters: The bandwidth of adjacent nodes is set to be infinite, whose delay is linked to the distance. The chain bandwidth of non-adjacent nodes is set to be 0, whose delay is set to be infinite. The bandwidth within the same node is set to be infinite, whose delay is set to be 0.

VNF parameters: The total number of VNF types is 8, and the resources occupied feature the 1–2 uniform distribution. Each VNF can handle any service chain.

SFC: The number of SFC is set to be 10,whose length follows the 2–6 uniform distribution, while the number of VNF follows the 1–5 uniform distribution, and the corresponding VNF resource demand is distributed. The bandwidth demand of the service chain features the 6–8 uniform distribution. All service functions are ranked by the service chain length and bandwidth demand in a descending order.

Chain connection overhead: To facilitate computing, the chain connection overhead of any adjacent node is set to be the comprehensive cost of the delay overhead and the bandwidth overhead by the weight. To highlight the optimization of delay, the delay overhead weight is 0.7,and the bandwidth overhead weight is 0.3.

VNF placement cost: When the resource capacity of functional nodes is adequate, the VNF of any type can be placed, and the corresponding capacity resources are deduced after functional nodes finish VNF placement.

4.2 Verification Algorithm

Referring to Section 3, this paper proposes an algorithm, which first embeds an SFC with the shortest overhead in the service chain. Then, the last VNF and all destination nodes construct a Steiner tree, and the node resources are updated.Thereby, the embedding of a service functional tree is finished.

According to the Greedy algorithm, each step looks for the node with the shortest path of the current node and the next node. The VNF is placed in order. After VNF placement is completed, the shortest path between the last VNF and the destination node is found to connect and update the node resources and to finish the embedding of a service function tree.

Under different parameter settings, the performance of these two algorithms are compared,which involves the total chain delay and total overhead and algorithm operation length of time.

4.3 Verification and Simulation

4.3.1 Influence of Service Function Chains

To assess the influence of the number of SFC,this paper subsequently uses two algorithms for placement of 10 SFCs. After 10 times of operation, the average is obtained. As shown in Fig. 1,combining the experimental data analysis, the randomly-generated service chain matrix length features 2–6 uniform distribution, and the service chain matrix is arrayed in a descending order. Therefore, when the service chain length is short, the performance period of these two kinds of algorithms is close to each other. When the service chain length increases, the time complexity of the Viterbi algorithm obviously exceeds the Greedy algorithm.

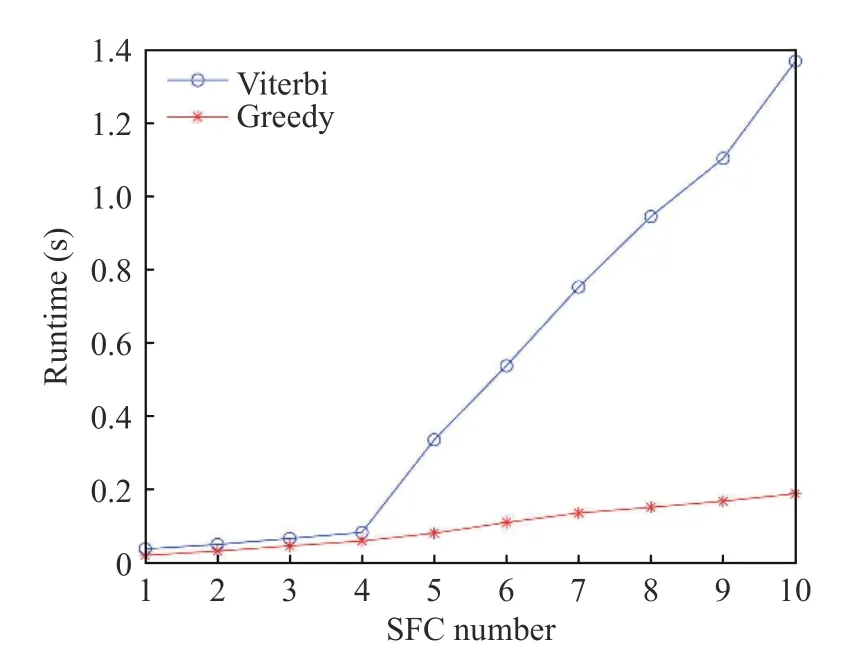
Fig. 1 Code operation length of time at different numbers of SFCs

According to Fig. 2 and Fig. 3, the Viterbi algorithm can efficiently reduce the overhead and delay of the chain. The overhead of the Viterbi algorithm is reduced by 13.66% on average in comparison with the Greedy algorithm, and the delay is reduced by 10.16%.

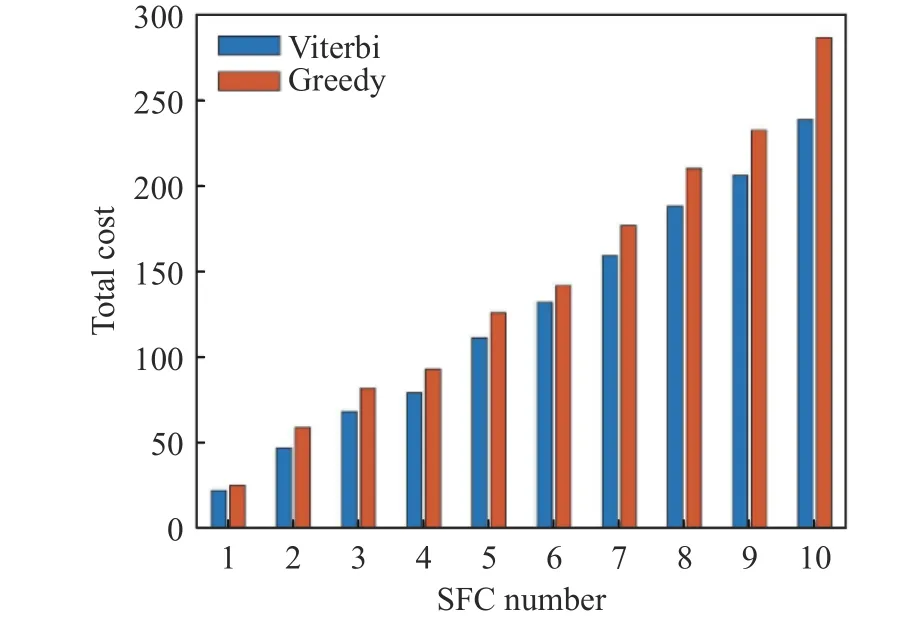
Fig. 2 Total overhead for placement of different numbers of SFCs

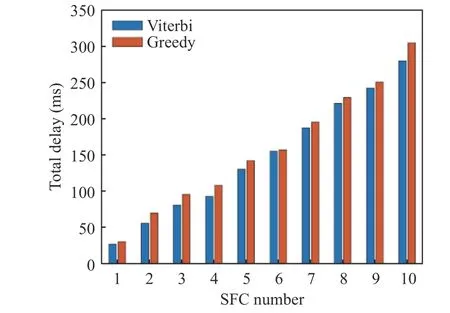
Fig. 3 Total overhead for placement of different numbers of SFCs

4.3.2 Influence of SFC Length

To assess the influence of the SFC length, this paper assumes the SFC length to be the integer of 2–6 subsequently. When there is a large number of SFCs, network saturation of the Greedy algorithm will appear. Then, the performance improvement of the algorithm is verified at different SFC lengths. Each time every five service chains are placed and operated ten times to obtain the average.

As shown in Fig. 4, as the SFC length increases, the number of VNFs for placement increases. The operation length of time of the Viterbi algorithm is obviously longer than that of the Greedy algorithm. As one observes in Fig. 5 and Fig. 6, when the network capacity is adequate, the deployment overhead and the SFC are linearly correlated. When the network is not fully loaded, the overhead of the Viterbi algorithm reduces by 21.9% on average compared with the Greedy algorithm, and the delay reduces by 7.192% on average.

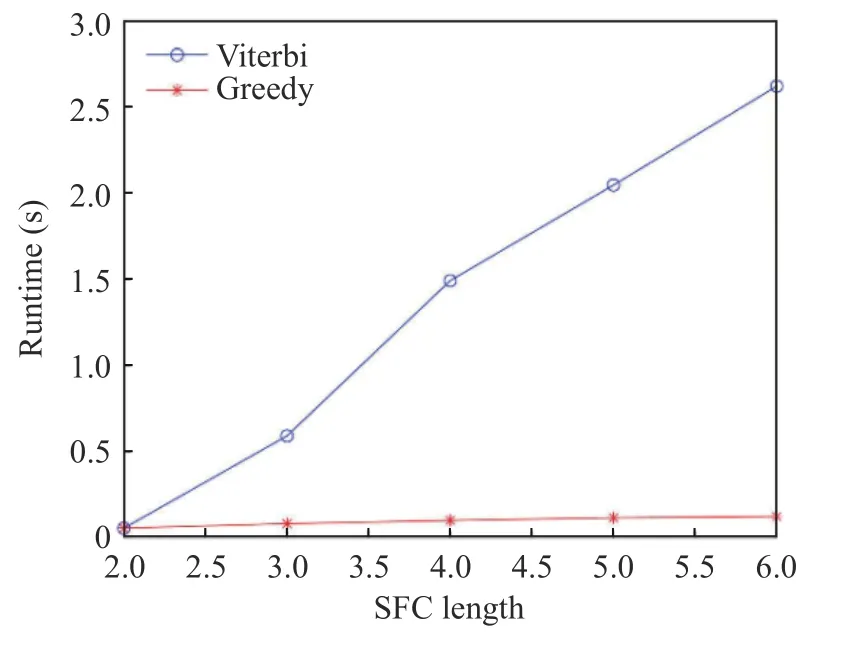
Fig. 4 Code operation time at different SFC lengths

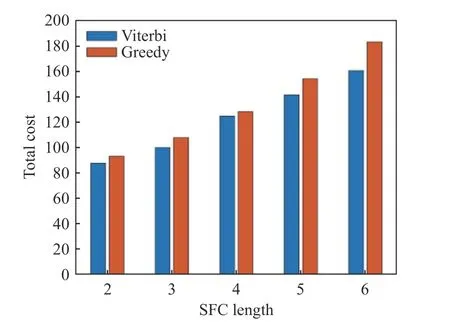
Fig. 5 Total overhead for VNF placement at different SFC lengths

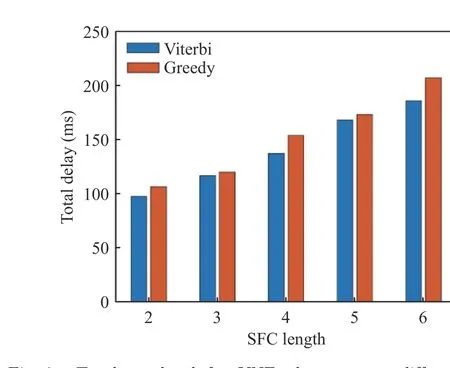
Fig. 6 Total overhead for VNF placement at different SFC lengths

4.3.3 Influence of the Number of Destination Nodes

To assess the influence of the number of destination nodes, this paper assumes the number of destination nodes to a random number from 2 to 6. 10 service chains are placed. The number of destination nodes is set to be a random number from 2 to 6. The average is obtained after operation for 10 times.

As shown in Fig. 7, the operation length of time of the Viterbi algorithm is obviously longer than that of the Greedy algorithm. As the number of destination nodes increases, the algorithm operation length of time is not changed significantly, because the algorithm operation length of time is mainly decided by the SFC embedding process. The construction of the Steiner Tree will not exert too much influence on the code operation time. As shown in Fig. 8 and Fig. 9, when the number of destination nodes increases, the overhead for the last destination node to be connected to the destination node will increase. The overhead of the Viterbi algorithm reduces by 37.9% compared with that of the Greedy algorithm. The delay reduces by 10.32% on average.According to the comprehensive overhead equation, when the number of destination nodes increases, the bandwidth overhead of the Viterbi algorithm is far lower than that of the Greedy algorithm.

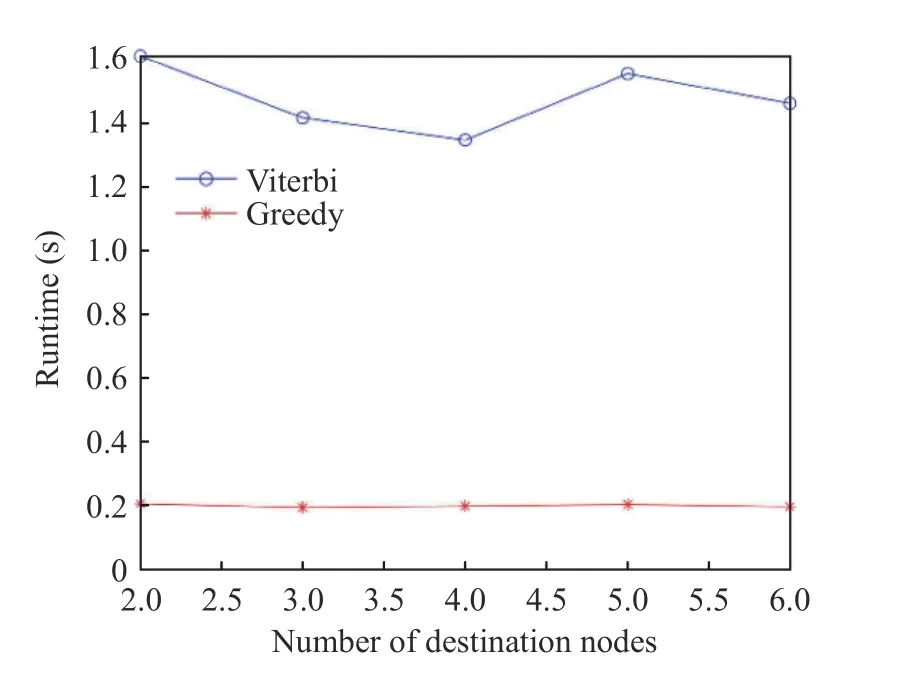
Fig. 7 Code operation length of time at different numbers of destination nodes

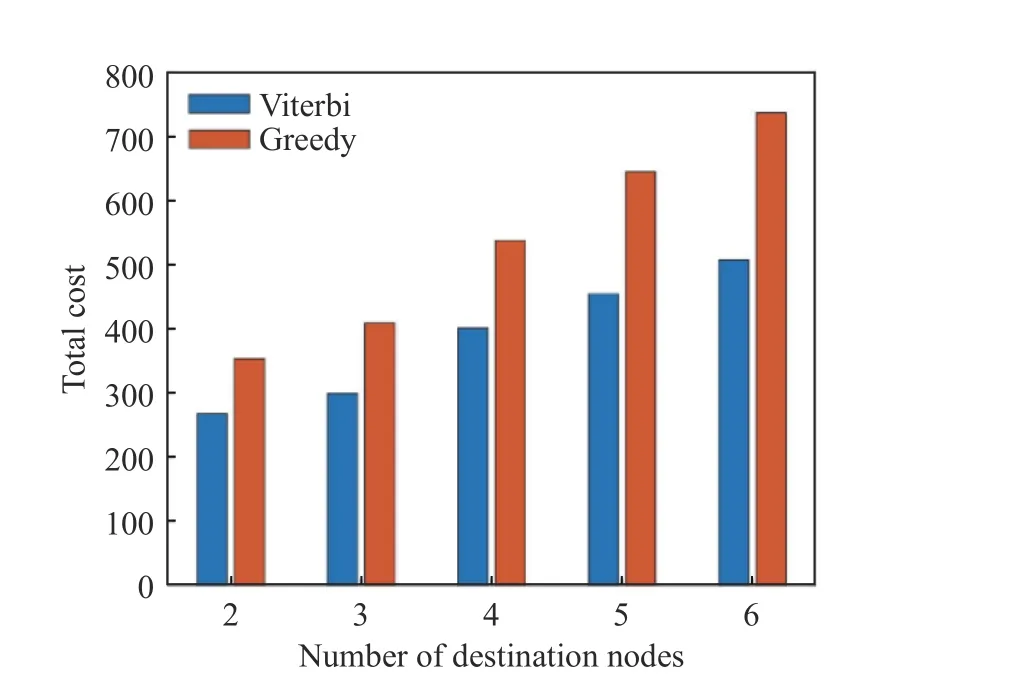
Fig. 8 Total overhead for placement of VNFs at different numbers of destination nodes

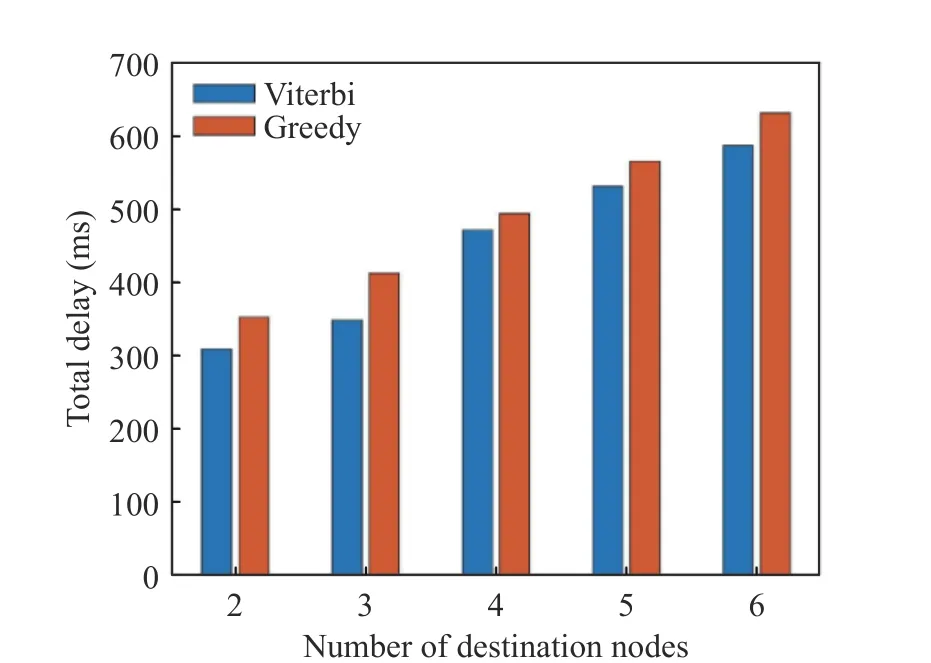
Fig. 9 Total delay for placement of VNFs at different numbers of destination nodes

5 Conclusion

This research examines the multicast NFS tree placement and establishes the mathematical model with the minimization of comprehensive overhead as the objective to verify the optimal NFS tree placement to be an NP-hard problem.Thereby, a two-stage algorithm is used to address the issue of function service placement.At the first stage, a feasible solution to the problem can be obtained through embedding of SFC.At the second stage, the Steiner Tree is established to realize embedding of the NFS tree.Through comparison, the optimal solution is obtained. The MATLAB simulation is used to compare the algorithm overhead optimization and study the algorithm performance, total overhead and total delay under different parameter settings. According to experimental results, the NFS placement approach based on the minimum spanning tree can reduce the total overhead by around 37.9% and the delay by 10.32% at most in comparison with the Greedy algorithm.

Future research can be carried out from the following perspectives. To optimize the algorithm performance in a large-scale real network,the performance of this algorithm proposed by this paper can be verified in a large-scale-real network. In response to dynamic changes of the underlying topographical network and SFC,topographical network changes and SFC migration and leaving should be considered. Not only should the placement of VNFs be considered, but their migration and release should also be taken into account. To optimize the algorithm model of unexpected traffic, researchers can think about how to reserve resources for unexpected traffic under the prerequisite of reducing the comprehensive overhead.

Acknowledgement

The authors would like to thank the associate professor Zhaoming Lu who is working at Beijing University of Posts and Telecommunications (P.R. China) in particularly for the support in thesis examination and guidance. The authors are also grateful to the teacher Luhan Wang of OAI WORKSHOP.