挖掘关联信息 回归基本模型

广东省广州市执信中学(510080) 朱清波

1 引言

椭圆中的定点定值问题是高考的热门考点,学生在引参探究时设点还是设线的选择思路往往不清晰,加上这类问题对运算能力要求较高,故一直是高三复习备考阶段较难逾越的一个知识点.查阅相关资料时,发现较多相关文章均是关于对此类问题的解法技巧, 缺乏对其性质生成背景的分析,只注重解题的教学活动很容易造成学生就题论题从而导致备考效果不佳.这些性质是孤立存在的吗? 能否统一转化到一个基本性质模型从而梳理出一个清晰的解题思路? 经过探究笔者发现此类问题源于椭圆的两个小性质,以此为基础再进行一些拓展即能产生一些新的结论,以下就从该性质展开说明.

问题1如图1,已知椭圆C:b ＞0)的右顶点为M, 过P(m,0)(m≠a)的直线l与椭圆交于A,B两点, 记MA,MB的斜率分别为k1,k2,证明:

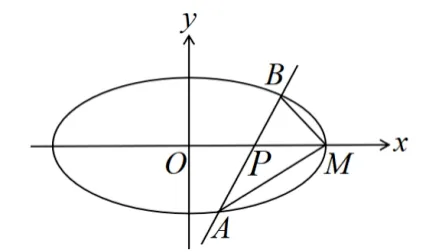
图1

证明(分类讨论)若直线l斜率k存在, 设直线为y=k(x-m),代入椭圆方程,整理得

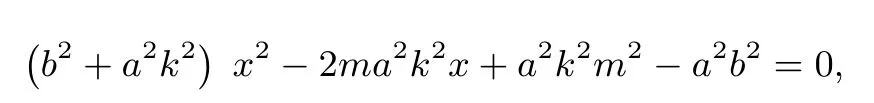
当Δ＞0 时,记A(x1,y1),B(x2,y2),则有

综上,命题成立.

利用上述问题的推导过程,可以发现椭圆存在如下两个性质:

性质1在问题1 的条件下, 若P(m,0)(m≠a)为定点,则MA,MB的斜率之积为定值

2 命题背景探究

围绕上述两个基本性质,重新审视一些高考真题和模拟试题中与之相关的问题,分析其考查特点后大致可分为如下几类:

2.1 结合平面几何背景考查定点定值问题

问题2如图2,已知椭圆过右焦点F2的直线l与C交于A,B两点,点P为椭圆的右顶点,直线PA,PB与直线x=4 相交于M,N,求证: 以MN为直径的圆经过点F2.

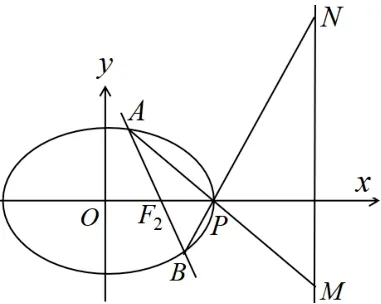
图2

图3

问题3(2018 全国新课标I卷第19 题)如图4,设椭圆的右焦点为F, 过F的动直线l与C交于A,B两点, 点M坐标为(2,0), 设O为坐标原点, 证明:∠OMA=∠OMB.

图4

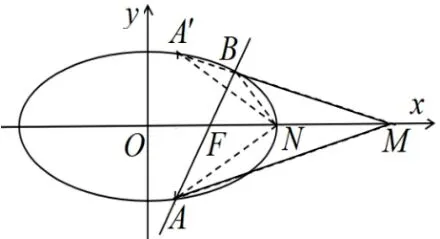
图5

若MB是椭圆的切线, 记B(x0,y0), 则MB方程为代入M(2,0)可知x0=1,即表明AB⊥x轴,利用对称性可知∠OMA=∠OMB.

2.2 结合椭圆中的基本性质来考查定点定值问题

椭圆有一个关于斜率之积为定值的的基本性质, 其具体形式如下:

图7

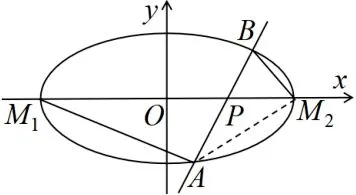
图8

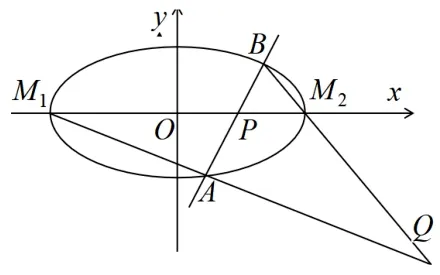
图9

图10

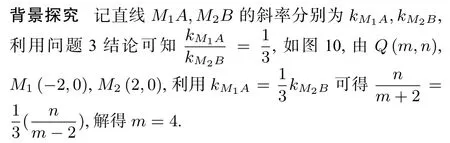
2.3 利用几个性质相互转化考查定点定值问题

问题6(2020年高考新课标I卷第20 题)如图11,已知A,B分别为椭圆的左右顶点,P为直线x=6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.证明: 直线CD过定点.

图11

图12

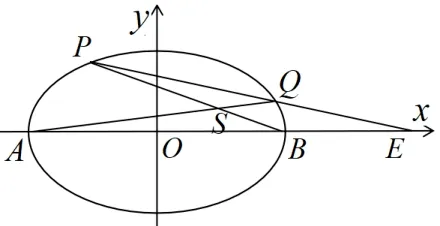
图13

图14

3 考查方式拓展

通过对上述几个问题的的背景探究,将某些问题中条件和结论简单置换,还可以作如下考查.

问题8如图15,已知椭圆左右顶点分别为A,B,动点S在直线x=1 上,连结AS,BS分别与椭圆交于P,Q两点,求证: 直线PQ过定点.

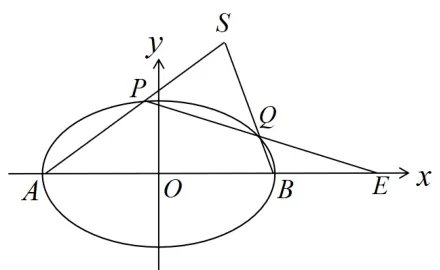
图15

命题思路记直线SA斜率为kSA,其余直线斜率表示类似,由S在直线x=1 上,设S(1,t),由

图16

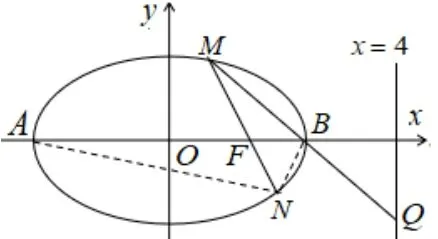
图17

数学家波利亚曾说,问题真正获得解决的评判标准应是我们对原问题的理解比刚开始时更完整和准确.对上述定点定值问题的研究若不深刻,极易将与之相关的解题教学活动变成题海训练,一旦问题情境发生变化就无法识别其本质导致束手无策.因此在解题探究中不仅要帮助学生总结归纳方法,还要充分剖析这些问题的命制背景,最终实现多题一解,若学生在日常的数学教学活动中不断地经历类似的深度思考与类比迁移,在后续的学习过程中亦能自发产生类似的深层次疑问并主动尝试交流或解决这些困惑,从而有效提升自身的数学核心素养.