棉织物含水率与悬垂性回归模型的建立
2022-11-02汪世奎
胡 冰,汪世奎
棉织物含水率与悬垂性回归模型的建立
胡 冰,汪世奎
(合肥师范学院 艺术传媒学院,安徽 合肥 230601)
本文通过悬垂性测试仪XDP-1对棉织物试样不同含水率下的悬垂性能进行测试。借助以六西格玛理论为基础的统计分析软件JMP对实验数据进行整理分析,分别建立了含水率与静态悬垂系数、动态悬垂系数、波峰幅值均匀度、波峰夹角均匀度、最大波峰幅值和最小波峰幅值的回归关系模型,并对其进行验证分析。
含水率;棉织物;悬垂系数
织物的悬垂性是指织物因自重而下垂的性能,反映织物的悬垂程度和悬垂形态[1],是对服装外观进行主观判断和评价的重要因素。用于衣料的纺织品,特别是裙料类的织物对悬垂性有一定的要求,能够形成光滑流畅的外观形态,具有良好的贴身性,给人以视觉上的享受。目前对织物悬垂性的研究主要集中在织物的力学性能,包括织物结构、纱线强力、拉伸强力、撕裂强力、硬挺度、弹性及回复力、耐磨性等对悬垂性的影响[2-5]。且上述研究均在织物处于干态下完成,其目的主要是倾向于开发悬垂性优良的新型面料。然而,鲜有湿态下即织物不同含水率状态下的悬垂性研究,湿态下织物悬垂性的不同会影响其洗涤、烘干及护理的方式。因此,有必要对不同含水率下织物的悬垂性进行分析与探究。
1 实验
1.1 试样
鉴于棉织物是人们在服装中穿用较多的一种织物,吸湿能力较强,且含水较稳定、较均匀,所以本实验中选取棉织物作为实验试样。试样规格如表1所示,为100%纯棉梭织物,组织结构为平纹组织。
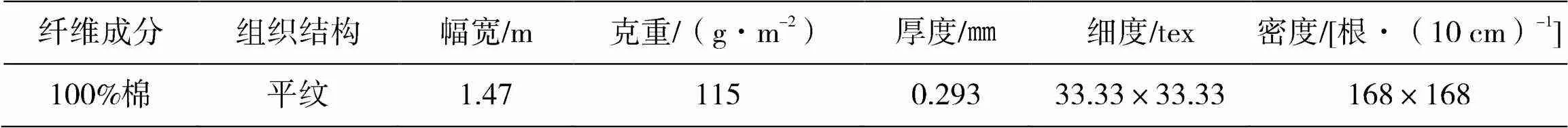
表1 试样规格
1.2 实验仪器
本次实验用到的仪器如表2所示:

表2 实验仪器一览表
1.3 实验过程
1.3.1 含水率的控制
考虑织物含水自然蒸发的特性,自制由渔线编制而成的格状沥水篮,使水分自然沥干及蒸发。此沥水篮由渔线编织,鱼线两端系绑在塑料篮的镂格上,结合一上一下的编织规律,使渔线可以均匀受力、相互支撑。渔线编织的位置靠近篮口,使渔线格网悬空,上下层空气自然流通,织物可以正反面同时蒸发水分,放置在温度为(20±2)℃、相对湿度为(65±4)%的标准环境下使织物能较为稳定和均匀的蒸发水分。
1.3.2 含水率的测试:
采用FA110Y电子天平进行测试,单位为g,称重精确到±0.001 g。对浸湿蒸发后湿重及干重称重结果进行计算确定织物含水率,其含水率计算如下:
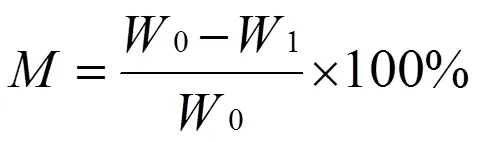
式中:M为织物含水率,%;W0为织物和水的总重量,g;W1为织物的干重,g[6]。
试样放置在温度为(20±2)℃、相对湿度为(65±4)%的标准环境下预处理24h后进行称重,此时重量记录为干重。将试样在水中浸没0.5~1h,保证水分浸透织物,而不是附着在织物表面。完全浸湿的试样放置于恒温恒湿室并平摊在自制的沥水篮上,在不同时间点对湿态蒸发的试样进行称重,通过含水率计算公式计算得到不同的含水率数值。
1.3.3 悬垂性的测试
在实验过程中,试样滴水现象的发生,会影响含水率的有效判定,同时也不利于悬垂性指标的测试,从而无法得出有效数据。经预实验验证,试样沥干、不滴水状态下的最大含水率范围为:55~60%,故将悬垂性实验的试样含水率临界值定为60%。标准大气条件下,试样在浸湿状态下自然蒸发称重计算所得的含水率最小值范围为:0~5%,将此状态默认为干态。测定含水率时进行3次称重取其平均值。
用XDP-1织物悬垂性测试仪来测量织物试样不同含水率下织物的悬垂性能,该测试仪是按照 FZ/T01045-1996 测试方法标准设计,采用国际通用的伞式法,利用图像处理技术测试织物的静动态悬垂性能的测试仪器[7]。测量指标包括静态悬垂系数、动静态悬垂系数之比、波数、最大波峰夹角、最小波峰夹角、波峰幅值均匀度、波峰夹角均匀度、最大波峰幅值和最小波峰幅值。试样裁剪成直径为24cm的圆,并且挖空圆心,试样准备36块[8]。
2 结果与分析
对36组实验的静态悬垂系数、动静态悬垂系数之比、波数、最大波峰夹角、最小波峰夹角、波峰幅值均匀度、波峰夹角均匀度、最大波峰幅值和最小波峰幅值进行相关性分析,其中动静态悬垂系数之比换算为动态悬垂系数。如表3所示,含水率与各指标间相关系数的绝对值大小排列为: 最大波峰幅值>动态悬垂系数>最小波峰幅值>波峰幅值均匀度>波峰夹角均匀度>最大波峰夹角>最小波峰夹角>静态悬垂系数>波数。

表3 相关性分析表
由表3可知,含水率与波数、最大波峰夹角及最小波峰夹角间的相关性较差,相关性系数分别为:0.038、0.322和-0.260。分别建立含水率与各指标之间的回归模型,均选择最优拟合次数进行拟合,其拟合模型相关性分析及方差分析如表4所示。含水率与波数、最大波峰夹角及最小波峰夹角间建立的模型的R方及调整后R方均小于0.3,F比分别为0.185、2.367、1.215,F比均小于3,P值为0.9662、0.0634、0.3244,均大于0.05,由此可知含水率与以上三个指标间建立的模型意义不大。
含水率与剩下指标间模型相关显著性排序为:动态悬垂系数>最大波峰幅值>静态悬垂系数>最小波峰幅值>波峰幅值均匀度>波峰夹角均匀度。其中含水率与静态悬垂系数间的相关性系数较低,但其拟合模型R方为:0.675,P值小于0.0001,即为显著相关,其模型具有显著意义。含水率与动态悬垂系数、最大波峰幅值、最小波峰幅值、波峰幅值均匀度、波峰夹角均匀度间建立模型的R方分别为:0.818、0.635、0.567、0.590和0.562,F比均大于6,P值均小于0.05,即为显著相关,其模型同样具有一定意义。
2.1 静态悬垂系数和动态悬垂系数
悬垂系数是反映织物悬垂程度的指标,根据织物的状态一般分为静态悬垂系数和动态悬垂系数。仪器测量织物悬垂性能时一般采用伞式法,即是将一定面积的圆形织物压于圆盘上,照射平行光线在投影屏上得到织物悬垂投影图,计算试样下垂部分的投影面积与其原面积之比的百分率,即为悬垂系数,通常悬垂系数越小,表示悬垂性越好。
由图1和图2可知,试样由干态到含水率达到10%~20%时,静态和动态悬垂系数均产生急剧下降。试样含水率为10%~20%时,悬垂系数均达到50%左右,悬垂性处于最优状态。此时试样重量没有大幅度增加,但遇水后柔软度变好,使其投影面积小于干态时投影面积。
当含水率超过20%时,动、静态悬垂系数发生回升,静态悬垂系数上升到75%左右,动态悬垂系数回升到80%左右,高于干态时的动态悬垂系数。随着含水量的增加,静态悬垂系数逐渐降低,即在含水率超过20%后,静态悬垂性逐步变优,并且优于干态状态下的静态悬垂性,而动态悬垂系数缓慢提高,在含水率达到30%后呈现出较为稳定状态。含水率达到20%后,随着含水率的增大,动态悬垂系数大于静态悬垂系数,即动态悬垂性差于静态悬垂性。
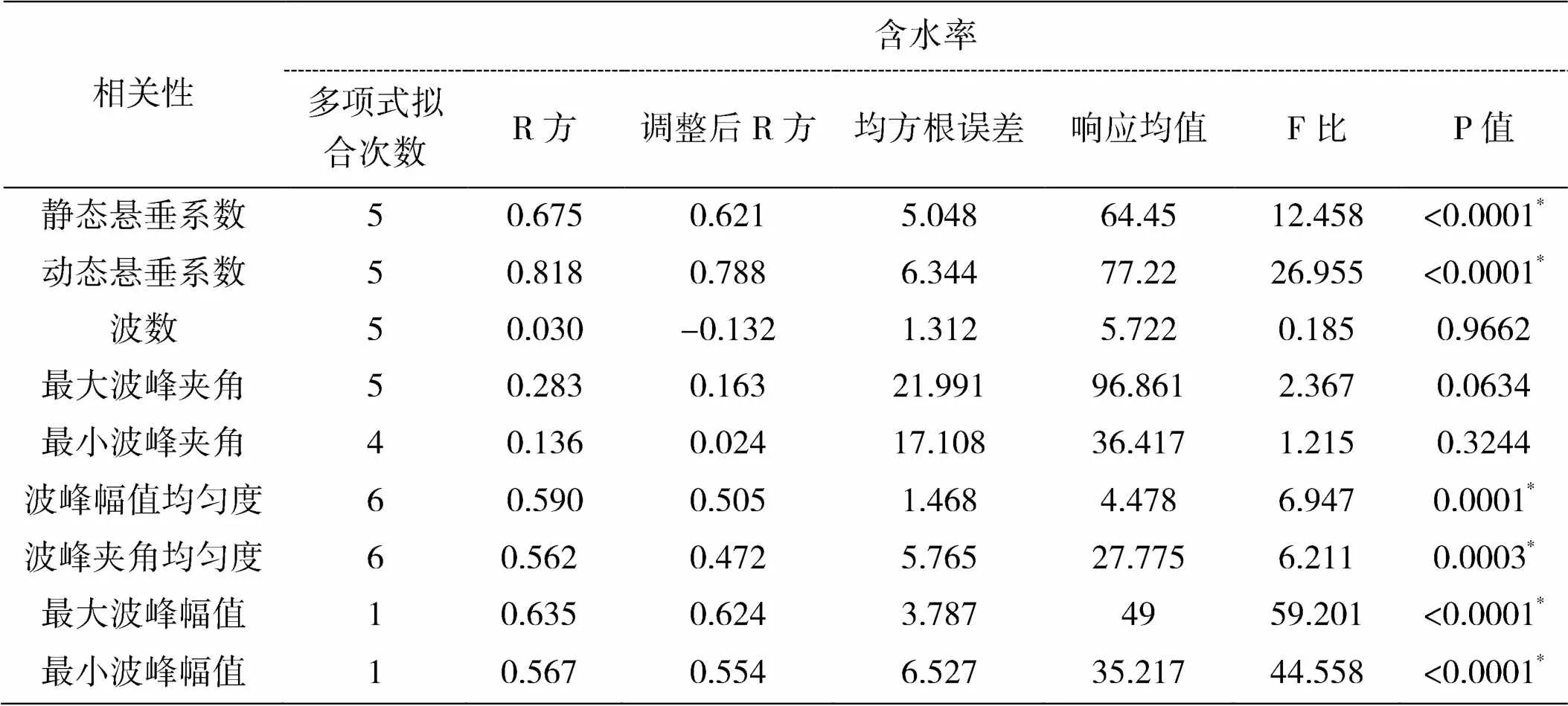
表4 拟合相关性及方差分析表
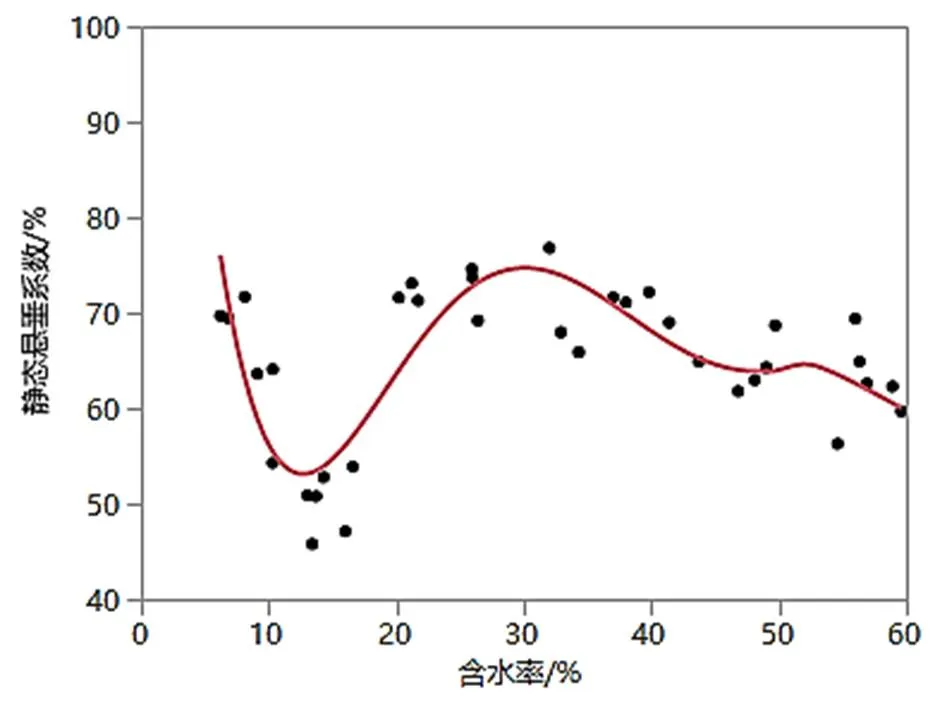
图1 含水率与静态悬垂系数的拟合关系图

图2 含水率与动态悬垂系数的拟合关系图
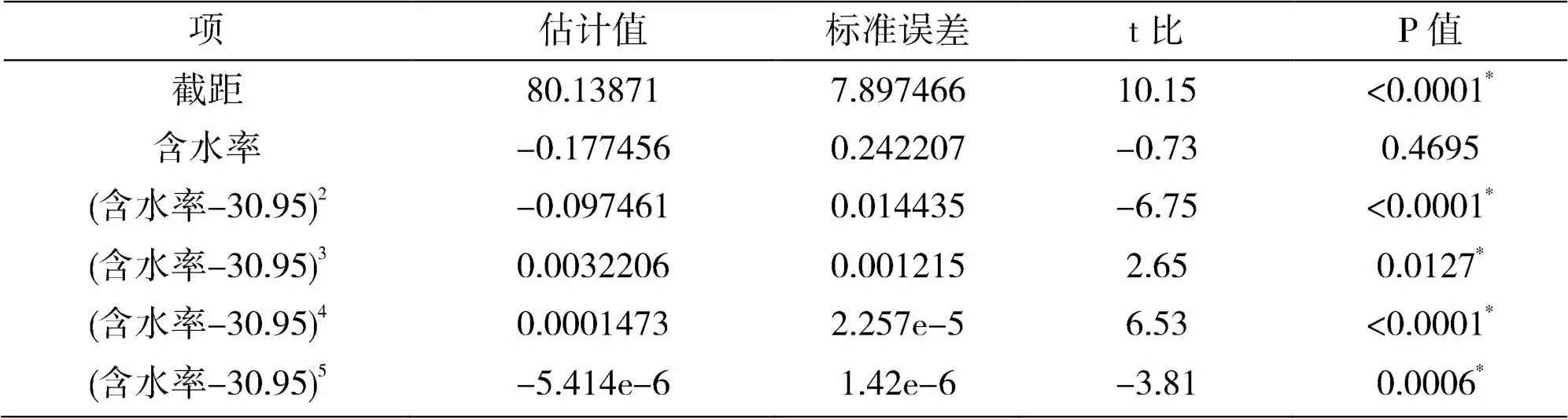
表5 含水率与静态悬垂系数的模型系数
分别对静、动态悬垂系数进行多项式拟合,得到线性回归方程。如表5所示,织物含水率与静态悬垂系数的线性回归方程为:
= 80.13871-0.177456×-0.0974607×(-30.95)2+ 0.0032206×(-30.95)3+ 0.0001473×(-30.95)4-(5.4138e+6)×(-30.95)5
为静态悬垂系数,单位为%,为织物含水率,单位为%,其中含水率项的P值大于0.05,其余项均小于0.05。
如表6所示,织物含水率与动态悬垂系数的线性回归方程为:
= 74.220403 + 0.4336891×-0.1003511×(-30.95)2+ 0.0028592×(-30.95)3+ 0.0001521×(-30.95)4-(5.1563e+6)×(-30.95)5
y为动态悬垂系数,单位为%,x为织物含水率,单位为%,其中含水率项和(含水率-30.95)3项的P值大于0.05,其余项均小于0.05。
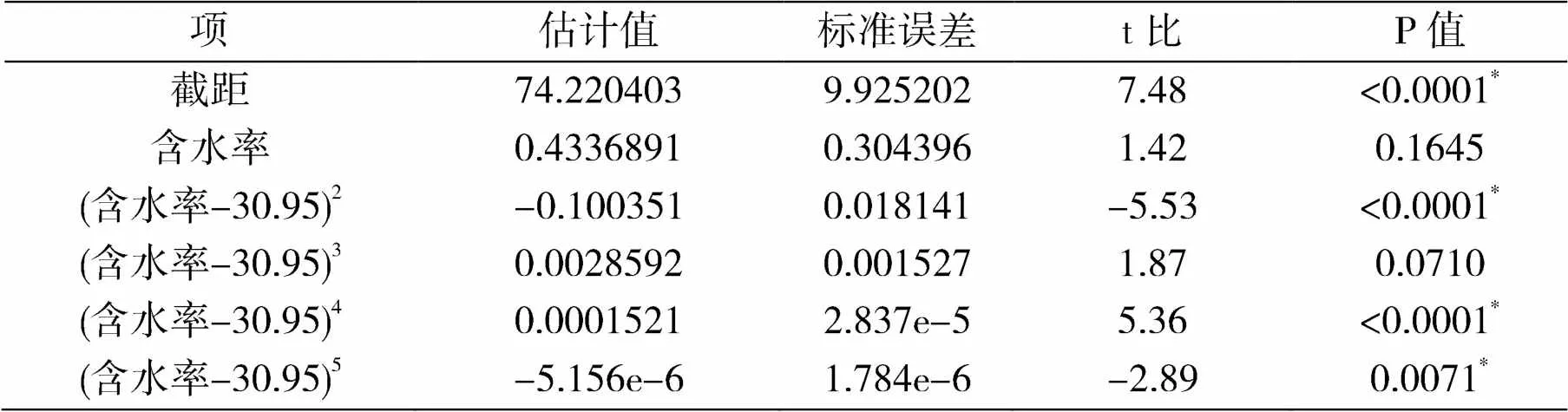
表6 含水率与动态悬垂系数的模型系数
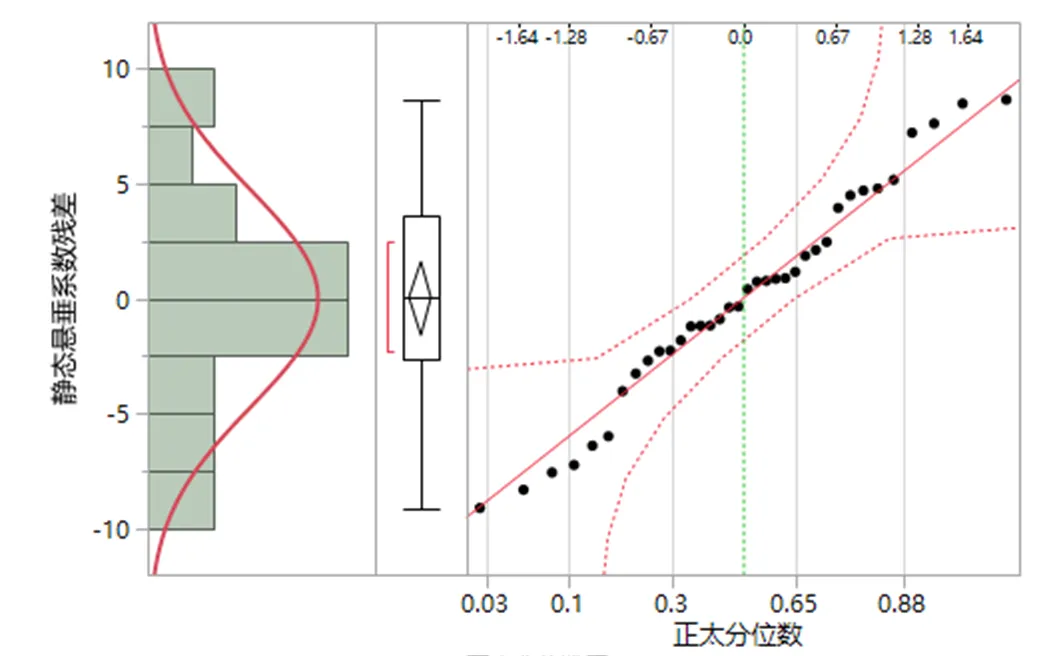
图3 静态悬垂系数残差正太分位数图
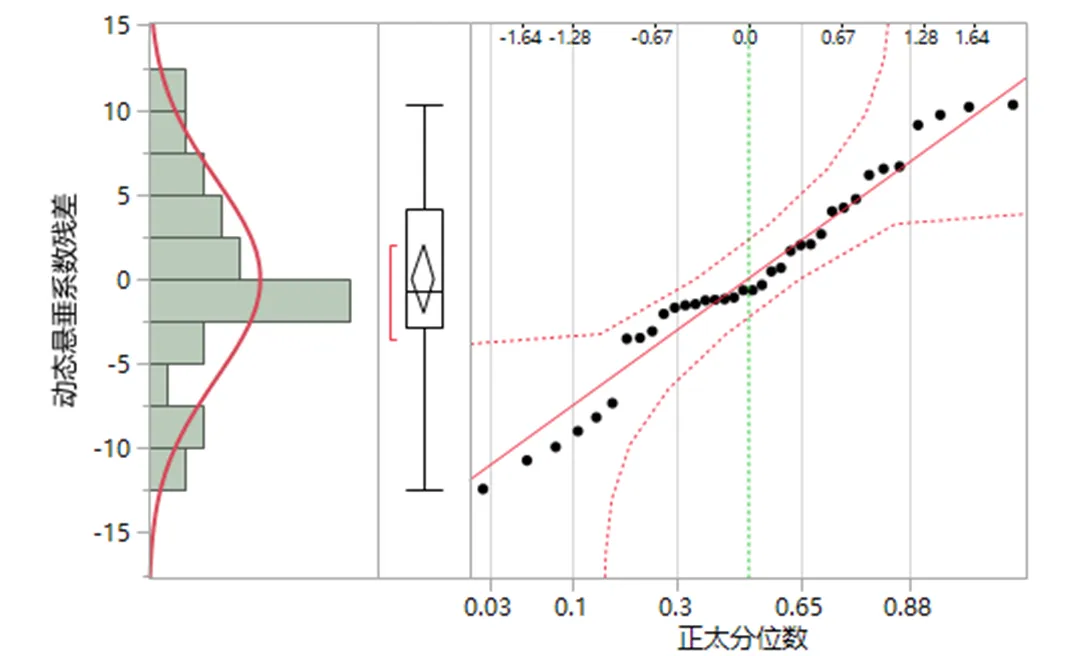
图4 动态悬垂系数残差正太分位数图
由图3和图4的静、动态悬垂系数残差正太分位数图可知,对回归方程的残差进行正太拟合,其拟合优度P值分别为:0.5485和0.2868,均大于0.05,假设成立,残差符合正太分布。且图中散点基本呈直线趋势,其模型均具有一定的准确性。
2.2 波峰幅值均匀度与波峰夹角均匀度
织物的悬垂系数主要用于评定织物的悬垂程度,结合对织物悬垂形态的评价可以更加全面地、客观地反映织物悬垂性能的优劣。波峰幅值均匀度及波峰夹角均匀度均是织物悬垂形态的评价指标,反映波峰凸出与分布情况,对织物悬垂性能的研究同样具有参考价值。
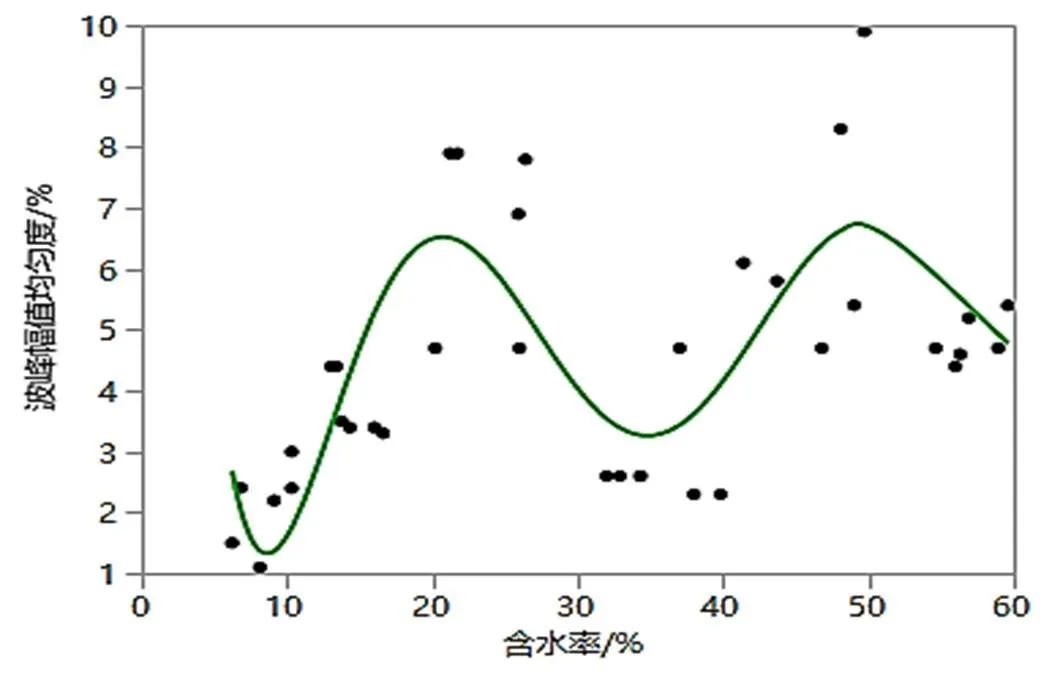
图5 含水率与波峰幅值均匀度的拟合关系图
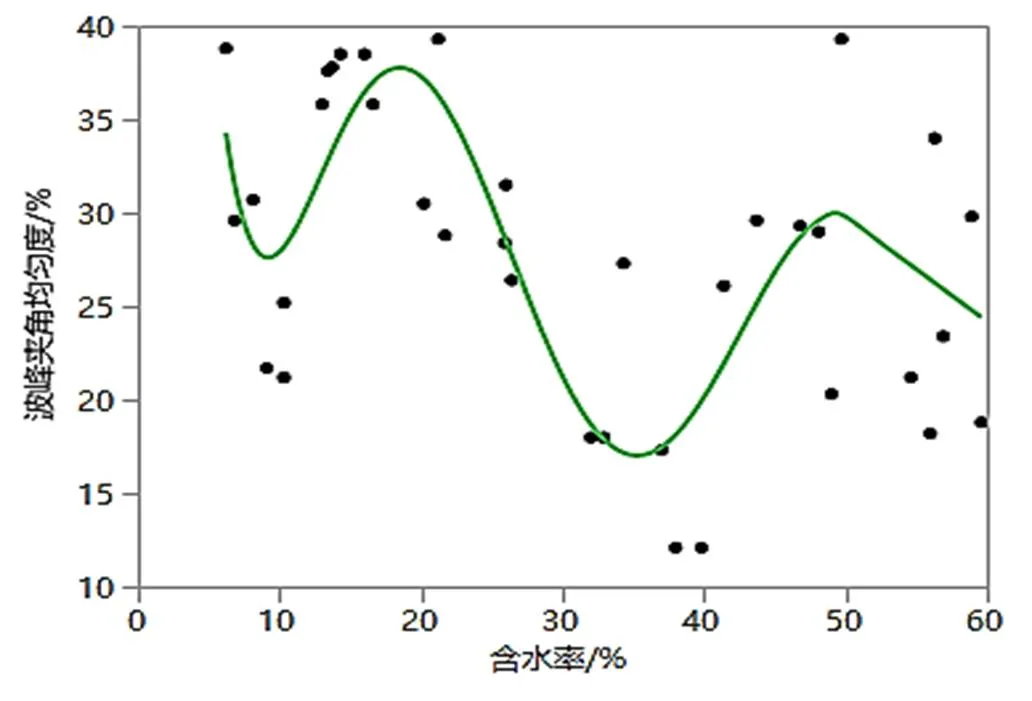
图6 含水率与波峰夹角均匀度的拟合关系图
如图5和图6所示,含水率与波峰幅值均匀度与波峰夹角均匀度之间拟合线呈现出波浪式变化。含水率从干态到10%时波峰幅值均匀度和波峰夹角均匀度小幅度降低,含水率接近20%时,波峰幅值均匀度和波峰夹角均匀度增加,并达到最佳状态,含水率30%~40%时波峰幅值均匀度和波峰夹角均匀度降低,含水率50%时又有所回升,大于50%时有一定幅度的下降。试样湿态下的波峰幅值均匀度优于干态。
如表7所示,织物含水率与波峰幅值均匀度的线性回归方程为:
=11.579524-0.252266×+ 0.0263054×(-30.95)2+ 0.0017001×(-30.95)3-(9.9113e+5)×(-30.95)4-(1.9604e+6)×(-30.95)5+ (9.2719e-8)×(-30.95)6
y为静态悬垂系数,单位为%,x为织物含水率,单位为%,其各项P值均小于0.05,表明该模型是显著的。
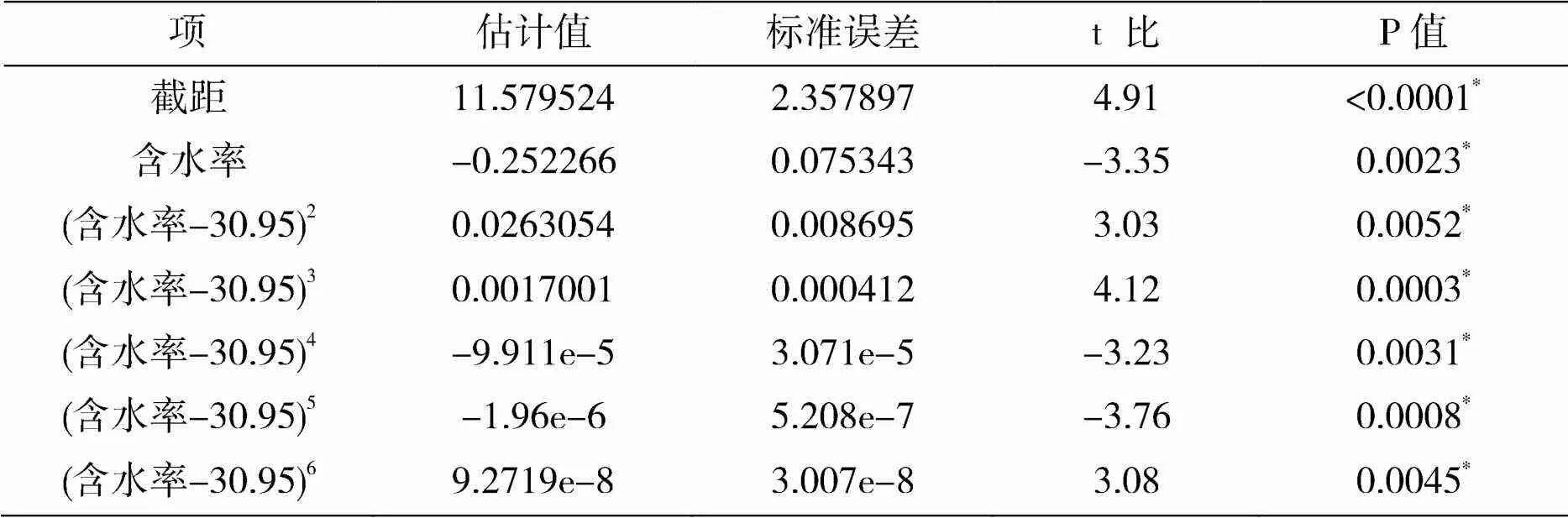
表7 含水率与波峰幅值均匀度的模型系数

表8 含水率与波峰夹角均匀度的模型系数
如表8所示,织物含水率与波峰夹角均匀度的线性回归方程为:
= 60.003774-1.2955206×+ 0.1274862×(-30.95)2+ 0.0060635×(-30.95)3-0.0004066×(-30.95)4-(6.9513e+6)×(-30.95)5+( 3.6618e-7)×(-30.95)6
y为波峰夹角均匀度,单位为%,x为织物含水率,单位为%,其各项P值均小于0.05,表明该模型同样是显著的。

图7 波峰幅值均匀度残差正太分位数图

图8 波峰夹角均匀度残差正太分位数图
图7和图8中的散点基本呈直线趋势,且对回归方程的残差进行正太拟合,其拟合优度P值分别为:0.3876和0.2364,均大于0.05,即波峰幅值均匀度及波峰夹角均匀度残差服从正太分布,其模型均具有一定的准确性。
2.3 最大波峰幅值与最小波峰幅值
描述织物的悬垂形态指标很多,最大波峰夹角与最小波峰夹角是对波峰凸出与分布情况中几种极限状态的评价。如图9所示,含水率达到15%时,最大波峰幅值出现高峰值,达到60mm,此后逐步降低,与含水率之间出现负相关关系。织物含水率与最大波峰幅值之间建立一元线性回归关系,尽管含水率在10%~20%时最大波峰幅值有一定的增加,但绝大部分实测值在预测模型95%的置信区间范围内或附近,未发生过多偏移。如图10所示,随着含水率的增大,最小波峰幅值逐渐变小,与含水率间同样呈现出负相关关系。其中个别实测值较大程度上偏离预测模型95%的置信区间,但大部分实际值在曲线范围内或附近。

图9 含水率与最大波峰幅值的拟合关系图

图10 含水率与最小波峰幅值的拟合关系图
含水率与最大波峰幅值间建立的回归模型R方为0.635,且结合表9可知,截距及含水率项P值均小于0.0001,说明模型显著性较高,有一定的意义。回归模型方程为= 57.666-0.28×,y为最大波峰幅值,单位为%,x为织物含水率,单位为%。该回归方程的常数项为57.666,含水率的系数为-0.28。如表10所示,织物含水率与最小波峰幅值的线性回归方程为:= 48.175-0.419×y为最小波峰幅值,单位为%,x为织物含水率,单位为%。且各参数P值均小于0.0001,表明该模型是非常显著的。

表9 含水率与最大波峰幅值的模型系数

表10 含水率与最小波峰幅值的模型系数
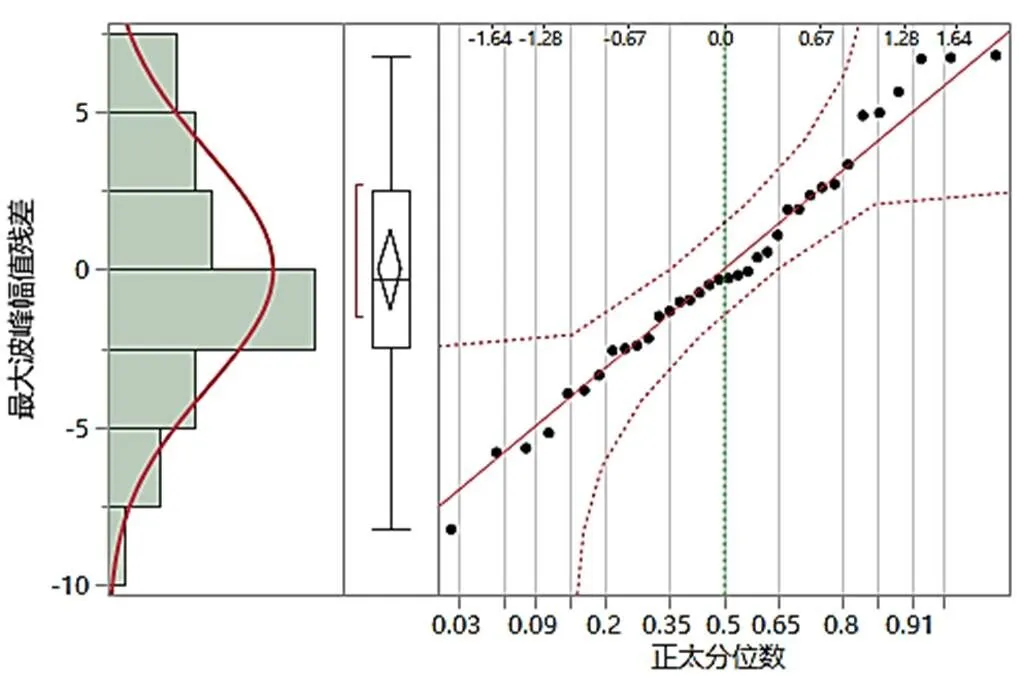
图11 最大波峰幅值残差正太分位数图

图12 最小波峰幅值残差正太分位数图
对回归方程的残差进行正太拟合,最大波峰幅值残差拟合优度P值为0.6639,大于0.05,且从图11的最大波峰幅值残差正太分位数图中可知,散点基本呈现直线趋势,残差符合正态分布。最小波峰幅值残差拟合优度P值为0.0011,小于0.05,且图12中部分散点有偏离情况,残差不符合正态分布。由此可知含水率与最大波峰幅值间建立的模型具有一定的准确性,而最小波峰幅值的模型准确性较低。
3 结论
本文为保持其他相关因素不变,选取了一种具有代表性的纯棉平纹织物作为实验对象,借助 JMP 软件进行数据分析,利用XDP-1悬垂性测试仪等相关实验设备,探究了含水率对棉织物悬垂性能的影响,建立含水率与悬垂性的回归模型,并分析其准确性。结果显示:含水率显著影响静态悬垂系数、动态悬垂系数、波峰幅值均匀度、波峰夹角均匀度、最大波峰幅值和最小波峰幅值;含水率与静态悬垂系数、动态悬垂系数、波峰幅值均匀度、波峰夹角均匀度和最大波峰幅值间建立的模型显著并具有一定准确性,而最小波峰幅值的模型尽管显著,但准确性较低。
实验试样的单一性使研究结论具有一定的局限性,今后若条件允许,应该采集更多不同种类的织物作为测试对象,以便更加全面地研究不同织物的含水率对悬垂性能的影响。
[1] 于伟东.纺织材料学[M]. 北京:中国纺织出版社,2006. 321-323.
[2] 王霞,罗戎蕾.织物悬垂性的研究现状及发展趋势[J].纺织导报,2021, (9):78-82.
[3] 杨红英.结构参数及后整理方式对棉织物悬垂性的影响[J]. 棉纺织技术,2021,49(4):33-36.
[4] 张萍,于学成,于悦. 织物悬垂性能的评价指标及影响因素[J].辽东学院学报 (自然科学版),2016,23(4):290-294.
[5] 郭红霞,赵万荣.竹纤维针织物悬垂性能对比及其影响因素的相关性分析[J].广西纺织科技,2010,39(1):19-21.
[6] 齐翀,向忠,胡旭东.纺织品含水率测量方法研究进展[J].现代纺织技术,2020,28(1):52-61.
[7] 韩新叶.基于CLO3D的织物悬垂性模拟研究[D].北京:北京服装学院,2016.
[8] 黄新林.织物悬垂性测试方法及其装置的研究[D].上海:东华大学,2011.
Establishment of Regression Model Between Moisture Content and Drapability of Cotton Fabric
HU Bing, WANG Shi-kui
(School of Arts and Media, HeFei Normal University, HeFei Anhui 230601, China)
The drape properties of cotton fabric samples with different moisture content were tested by XDP-1 drape tester. The experimental data were analyzed by the statistical analysis software JMP based on six sigma theory, the regression models of moisture content with static drape coefficient, dynamic drape coefficient, crest amplitude uniformity, crest angle uniformity, maximum crest amplitude and minimum crest amplitude are established and verified.
moisture content;cotton fabric;drape coefficient.
胡冰(1990-),女,讲师,研究方向:服装舒适性、服装数字化设计.
安徽省哲学社会科学规划项目(AHSKY2020D110).
TS103.923
A
2095-414X(2022)05-0069-07
