始于“自然而然”终于“贯通了然”——整体性视角下人教版“中括号”的教学探寻

文|金滢

一、基于整体看“括号的认识”编排：有序推进，自然生成

以人教版为例，两步混合运算分散在四册教材中进行学习，在一二年级依次经历了“连加连减——加减混合——认识小括号——乘加乘减——加减乘除混合”这几个阶段的学习，二年级下册第五单元《混合运算》是对前面所学知识的一个梳理和总结。第一学段两步混合运算与小括号认识的学程细腻而缓慢，关键例题都结合具体情境，可以让学生充分了解四则运算的意义。

四则混合运算的难点是括号的使用，而到了第二学段，中括号的出现将四则混合运算的学习带入新的高度，它让运算的顺序变得更加多变，也更加复杂。四年级下册的《括号》一课既带领学生认识“中括号”，同时也是整数四则混合运算的收官课，容量大、思维含量高，但教材却以最直接、最简单的方式告诉学生：一个算式里，既有小括号，又有中括号，要先算小括号里面的，再算中括号里面的。

那么，这样的方式是否适合每个学生呢？小括号的使用方法是否能直接被迁移？学生是否真正理解中括号的意义呢？

二、基于课例看“中括号的认识”实践：形式有余，本质难达

教学中许多教师都紧紧抓住了“中括号改变运算符号”这一核心，通过“24 点”“合并算式”等形式激发学生创造“中括号”的需求，在讨论交流中明晰“中括号”的使用方法和四则混合运算的计算法则。看似“基于学情”的设计背后，却暴露出诸多“漏洞”。

1.高起点引入——云里雾里。

在课的引入环节，有教师通过把“2×6=12，12÷3=4，24-4=20”“8-2=6，24÷6=4，4×7=28”和“1+5=6，12÷6=2，56÷2=28”三个层次的分步算式合并成综合算式展开。但是很多学生无从下手或者错误应答，失去了学习的兴趣。

其实，早在二年级下册的混合运算单元练习中，人教版教材就出现了上述合并综合算式的练习，尽管当时只有两步计算，但这类练习却是错误率最高的。可见，教学不可只追求创意，基于学情，前后关联才是明智之举。

2.简单化迁移——漏洞百出。

递等式计算过程的展开环节，许多教师原先认为“学生能自主迁移”。把递等式计算简单化处理的背后是对学情的盲目和不理解，以及对教材认识的不到位，导致计算漏洞百出。

3.优生化替代——表面建构。

无论是“算式合并”还是“算24 点”，当对选择的学生的材料进行再加工时，“中括号”确实能呼之而出。但往往集中在部分学生中，他们能直击问题所在，并通过“中括号”解决运算顺序问题，而很大一部分学生始终处于能“听懂”却“不会用”的状态。

三、立足教材学情实现“中括号的认识”重构：扎根本质，贯通了然

《数学课程标准（2022 年版）》中关于“数与运算”的内容要求中明确指出：第一学段是在具体情境中，了解四则运算的意义；第二学段是在解决简单实际问题的过程中，理解四则运算的意义，能进行整数四则混合运算，正确运用小括号和中括号。可见，情境是理解意义的基础，意义是学习最终的指向。本着整体性和结构性教学思想，笔者以为，寻找相关知识、方法和思想的连接点，才能让学生真正掌握括号的意义和应用。

1.合理借鉴，特写教材留白的内容。

浙教版教材在中括号之前一共安排了七个例题的学习。这个学习的过程恰好对应人教版教材学习两步混合运算的路径。教学中应基于人教版教材有所取舍地进行补充，把从形式上看具有类似结构的算式作为混合运算拓展的切入点。

2.创编情境，意义的学习有章可循。

数学课程的整体化，要凸显对数学本质的理解，应引导学生从混合运算的原理和法则之间的联系出发，建立起有意义的知识结构。

（1）变式追寻本质，让知识生长有“根”。

从最基本的题型入手进行教学。引入新课后，教师出示12-4×2，让学生说一说运算顺序。

【教学放大镜一】

第一次变式：如果让算式长出翅膀96÷12-4×2 你还会算吗？试着算一算。

收集资源后进行反馈交流：

对比一：

（1 号生成材料）

（2 号生成材料）

交流问题：没有小括号的三步混合运算中先乘还是先减？引导学生从“8-4×2”这一步联想到以前学习的两步混合运算顺序。

对比二：

（2 号生成材料）

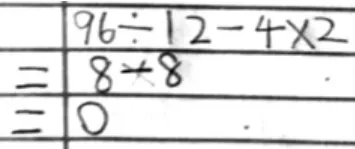
（3 号生成材料）

交流问题：除和乘能同时计算吗，能不能举出一个数学问题来说明可以同步计算？通过实际问题充分说明这里的乘和除可以同时计算。在此基础上，进一步追问，如果算式改成“96-12÷4+2”还能两边同时计算吗？为什么？以此突破前测中错误率最高的混合运算类型。

第二次变式：聚焦到上文1号作品，追问如果要按照这样的运算顺序，原题可以进行怎样的改变？引出小括号算式（96÷12-4）×2。并让学生创作：小括号除了加在这里，还可以加在哪里？通过对比进一步深刻体会有小括号混合运算的运算顺序。

（2）情境助力模型，让中括号有“意”。

通过情境链接运算的分步与综合，能让学生更加深刻地理解中括号产生的必要性以及运算顺序的合理性。

【教学放大镜二】

依次出示题组，让学生选择用哪个算式解答，以情境解读刚才的混合运算含义，并通过问题引发中括号的使用：从分步计算——合并成综合算式——中括号不同形式表征的异中求同来完成对含有中括号的算式的意义理解。

反馈层次一：分步计算，联系算式意义。

反馈层次二：将分步计算合并为综合算式后出示两幅错误作品。

让学生进行辨析，得出第一幅作品算完小括号里的以后，要先算96÷8，不符合刚才的思路；第二幅作品没有用一个完整的综合算式。在对比交流中，结合问题情境形成以下板书：

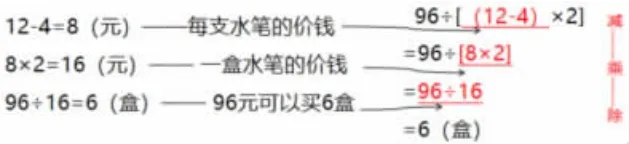
（3）抽象脱离情境，化整为零联系“运算本源”。

运算教学既要让学生理解算理，也要掌握算法，混合运算的学习同样需要这样推进。在脱离具体情境聚焦到算法的提炼的环节，追问学生“在这递等式计算中，你找到了哪些我们以前学的混合运算算式？”根据学生回答，电脑演示从算式中进行剥离（如下图）。

通过局部到整体，再由整体关注到局部，着眼于整个知识体系的视角，有效打通了两步计算和三步计算之间的本质联系。

（4）超越“运算顺序”，添加符号体会“结果唯一性”。

一直以来，“括号”用来改变运算顺序的作用深入人心，却忽略了改变运算顺序背后的数学实质是确保运算结果的唯一性。

【教学放大镜三】

出示360÷48÷12+4，根据这个算式添加不同的括号并进行计算。

1 号作品

2 号作品

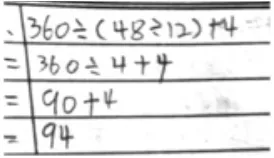
3 号作品

交流添了括号后运算顺序是否正确后，学生发现：

生1：数相同，运算符号也相同，得数不同。

生2：括号的位置不同，造成运算顺序也不同，所以计算结果也不同。

生3：如果没有规定的括号，不同的人添加的位置不同就会有各种结果。

师：添加的括号位置决定了运算的顺序，也就保证了运算结果的唯一。

紧接着对比1 号作品和4 号作品，通过比较把学生的思维引向深入：

1 号作品

4 号作品

师：添加的括号不同，什么相同？

生1：运算顺序相同，结果也相同。

生2：看上去符号不同，其实都是先算48÷12，再算4+4，所以中括号在这里并没有起到作用。

生3：添加的括号要有效，否则就是画蛇添足。

至此，学生对于括号的使用有了更加理性的思考，也对括号改变运算顺序使得运算结果唯一有了深入的体验。

综上所述，对于数学规定性的知识，同样需要厘清它的体系，基于整体性视角赋予有意义的学习，让学生经历知识发生的过程，而不是直接告诉结论。如此，才能让学生主动地学习，更加深刻地理解“规定”的来龙去脉。