自适应带宽核密度估计在旋转机械劣质监测数据识别中的应用
2022-10-31倪泽行王琇峰
倪泽行 王琇峰 徐 波 李 睿
西安交通大学机械工程学院,西安,710049
0 引言
随着传感器和测试技术的进步,现代监测与诊断系统在许多领域得到了迅速的发展[1]。现代监测手段是通过建立传感器网络收集状态监测信号以反映机械制造设备的运行状况,但由于待监测设备数量大、设备测点多、采样频率高、设备服役周期长,运行状况监测系统获取了海量的监测数据,推动机械设备健康监测领域进入了“大数据”时代[2]。然而,由于环境变化、传感器故障、人为干扰、电气故障等原因,数据的准确性和完整性被严重削弱,从而使监测指标突变,造成系统“误判”及维护策略制定不当[3]。因此,如何准确识别机械装备运行过程中的劣质监测数据对提高机械装备健康评估准确性具有重要意义。
机械装备全寿命监测数据主要为设备正常状态数据、设备退化数据、异常数据以及不能正常表征设备状态的劣质数据[4]。设备的退化多满足“浴盆曲线”,在设备正常阶段,监测数据的统计特性较为一致,多呈现为平稳特性。然而,随着设备出现退化,信号逐渐呈现为高阶平稳,而劣质数据也多表现为非平稳特性[5]。为了有效区分劣质数据与设备的状态数据,基于距离[6-7]、基于聚类[8-9]和基于统计特征[10]的异常数据检测方法被大量研究。其中,基于统计特征的检测方式因鲁棒性好、计算效率高等优点而被广泛接受。
基于统计特征的检测方法主要是通过数据的分布特点进行阈值识别。DUDAR等[11]用正态分布对金融数据的异常点进行识别。SREEVIDYA[12]总结了基于统计的异常检测技术在异常数据识别方面的应用,指出数据集的分布模型能识别概率较低的异常点。STEFANIAK等[13]选择合适的数据分布和统计参数,进行多维数据分析,以确定有效的识别机器及其部件状态的阈值。上述研究假设这些数据均满足特定的分布,通常情况下,不同的监测趋势数据分布是不确定的,而基于非参数化方法的异常检测无需事先假设数据的统计模型,而是基于数据集本身统计特性确定数据分布特征。JABLONSKI等[4]对比分析了正态分布、威布尔分布、极值分布及核密度估计在气体压缩机监测过程中异常数据的识别能力,发现核密度估计在数据流异常时识别准确率最高。值得注意的是,核密度估计的精度主要取决于带宽的选择,不同的带宽获得的分布特点不同,其阈值也不同。
为了自适应选择带宽,李国庆等[14]采用渐进积分误差法为扩散核函数选取自适应最优带宽,提高了光伏出力模型的局部适应性。CHEN等[15]提出了自适应加权局部在线密度估计,实现核密度带宽的自适应选择。牛文铁等[16]采用四叉树算法实现了自适应带宽核密度估计。上述方法为带宽的自适应选择提供了不同的思路,其核心都是通过不同优化算法得到最优的带宽序列。然而,这些优化算法同样存在先验参数选择问题。尽管优化算法给出了参数选取的经验公式,但参数不合理同样会导致估计偏差[17]。
本文针对上述问题提出了一种基于局部均值误差最小的自适应核密度估计方法,并应用于旋转机械劣质监测数据识别。该方法通过对监测时域信号的频域积分后的峭度指标进行统计分析,根据局部均值误差最小的准则优化带宽,实现最优带宽选择,从而获得最符合数据分布的概率密度曲线。最后根据95%的置信区间进行阈值选择,并采用工程数据验证所提方法的有效性。
1 基于概率密度估计的异常数据识别策略
旋转机械监测劣质数据识别的核心是通过设置有效的阈值对不能正常表征设备退化的劣质数据进行识别。阈值设置对监测的影响如图1所示。若阈值设定过高,则会将异常点判定为正常,造成劣质数据识别不全;若阈值过低,则容易将正常数据标记为异常样本,造成监测的误报。因此只有合理设定阈值,才能准确识别劣质数据。

图1 阈值设置示意图Fig.1 Schematic diagram of threshold setting
基于概率密度的劣质数据识别方法流程如图2所示,主要步骤如下:
(1)根据现有的历史监测数据,计算对劣质数据具有高敏感性的监测指标,最大限度实现劣质数据识别;
(2)根据上述计算所得指标获得相应的统计分布规律;
(3)选用合适的分布函数对统计分布规律进行拟合,以分布函数的95%置信区间对应的边界作为劣质数据判定阈值。若该监测指标超出阈值则认为该采集样本数据为劣质数据,反之正常。

图2 劣质数据识别策略Fig.2 Exceptional data identification policies
2 异常监测数据自适应识别方法
2.1 核密度估计
核密度估计基于非参数拟合方法,在数据分布先验知识未知的情况下实现参数分布的最优拟合,构建数据分布模型。
核密度估计基于经验密度函数提出,设X1,X2,…,Xn是数据集X中的样本,x1,x2,…,xn是对应样本的观测值,则在数据对应的频率分布直方图中,满足
(1)

频率分布直方图中,区间内的样本数越多,对应区间的概率密度越大。
在经验密度函数的基础上构造以样本观测值x为中心、区间长度h为直径的邻域,用样本观测值落入邻域的个数估计观测值x对应的概率密度。设函数K(x)符合密度函数特性,即
(2)
则可以将函数K(x)称为核函数,一般情况下选择高斯分布函数。基于核函数构建观测值分布的核密度可表示为
(3)
根据式(3),可以利用核密度函数对历史已知数据观测值分布特征进行拟合,从而获得当前数据集观测值分布模型。值得注意的是,不同带宽h的选择直接影响分布的拟合效果,h过大会使估计结果过于平滑,掩盖数据结构,h过小会产生过多的数据噪声[18]。通常情况下,我们希望的是数据密集点处采用小带宽,而数据分布稀疏的地方采用大带宽。
2.2 所提方法的步骤
为了识别监测过程的异常数据,本文提出了一种基于自适应核概率密度估计的劣质监测数据识别方法。该方法通过对采集的机械信号进行指标计算,然后针对该指标进行核密度估计,最后将95%的置信度进行阈值划分,从而进行异常指标识别。由图3可知,具体步骤如下:
(1)根据监测的历史样本数据进行异常指标计算。针对旋转机械常见的异常数据类型,如零点漂移、局部噪声等,通过对信号进行频域积分处理即可将突变特征转变为冲击特征,计算积分的峭度指标:

图3 所提方法流程Fig.3 The flow of the proposed method
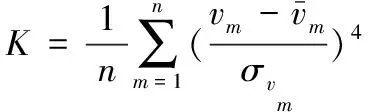
(4)

假设x(t)经傅里叶变换为A(ω),则
(5)
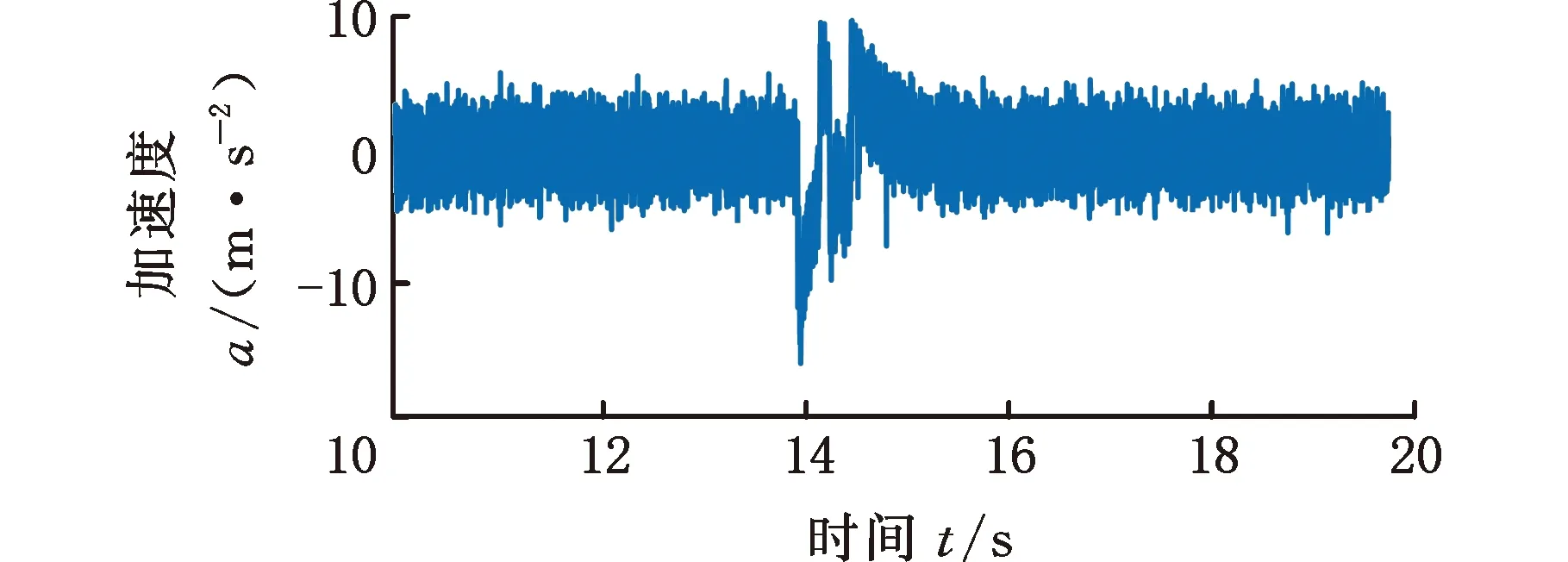
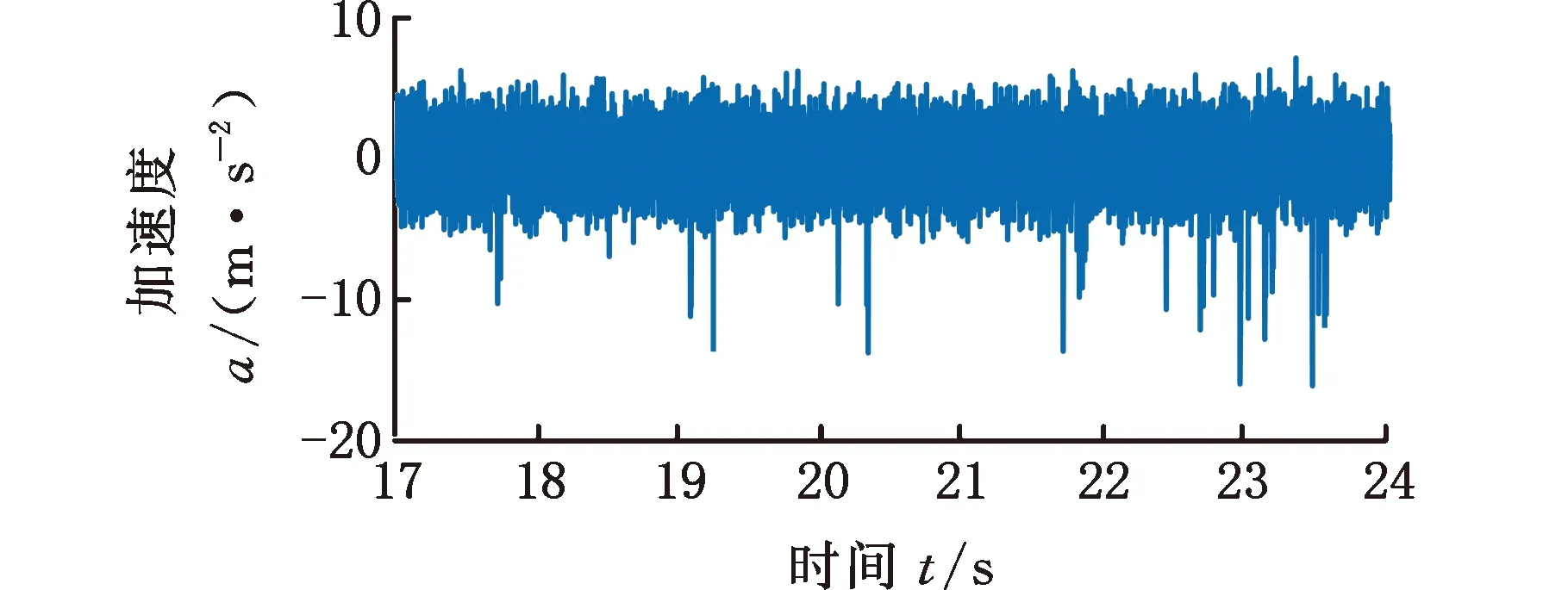
式中,Δf为频率分辨率;H(ω)为开关函数,当fd<ωΔf (2)基于自适应高斯核密度估计的积分峭度指标统计分析。本方法采用高斯核密度函数: (6) 式中,s为监测指标序列的元素,s=Ki。 选择不同带宽优化整个观察样本间隔估计的拟合优度。用可变带宽wt估计的峰值速率由下式给出: (7) 可变带宽wt作为在局部间隔内优化的带宽。在这种方法中,wt用于局部优化的区间长度调节函数的形状,从而获得最优的拟合优度。为了选择用于局部优化的区间长度,在t时刻引入局部MISE准则: (8) 减去与w的选择无关的项,引入t时刻的局部成本函数: (9) 为了实现自适应带宽的选择,引入了局部MISE进行不同带宽的选择,其估计成本函数为 (10) p,q=1,2,…,N (11) 式中,N为监测指标的数量,即采集的数据组数。 (12) 则考虑可变带宽的损失函数可以描述为 (13) (3)根据步骤(2)获得概率分布函数,计算95%置信度的边界线作为异常数据的报警阈值。 下面通过车桥耐久试验的全寿命数据对提出的方法进行分析及验证。 车桥疲劳试验台如图4所示,试验台有3个驱动电机,其中一端与车桥的输入端相连,用于动力驱动,其他两端与车桥的轮边相连,用于负载。为了监测车桥传动链的健康状态,通常在桥壳及轴承座处添加振动加速度传感器,传感器为CTC公司的AC103。参照车桥坐标系建立测试系统坐标系,设定如下:Z轴沿车桥输入轴轴向并平行于试验台面,X轴沿车桥输入轴径向并平行于台面,Y轴垂直于X、Z轴。采样频率为3886 Hz,每2 min采集一组数据,每组采样30 s。 图4 车桥疲劳试验台Fig.4 Axle fatigue test bench 某次车桥耐久试验的开箱结果如图5所示,车桥输入圆锥齿轮的齿顶处存在明显的剥落。 图5 圆锥齿轮剥落Fig.5 The peeling off of bevel gear 输入端轴承座测点的振动加速度有效值监测趋势如图6所示。可以发现,早期监测指标较为平稳,而368 min(第184组)数据出现拐点,指标明显呈上升趋势,其中在平稳阶段出现了明显的异常点。观察该指标对应的原始信号发现,造成指标突变的主要原因是采集的数据质量缺失,主要表现为零点漂移及局部噪声,如图7所示。 图6 监测趋势Fig.6 Monitoring trends (a)零点漂移 (b)局部噪声图7 信号时域特征Fig.7 Time-domain characteristics of signals 采用本文提出的指标分别对劣质监测数据、正常数据及故障数据进行分析,结果如图8所示。图8中,频域积分处理过的零点漂移及局部噪声信号均表现为非平稳特性,时域信号中均出现明显的局部冲击;而正常及故障状态的振动加速度信号经过频域积分处理后仍表现出较好的循环平稳特性。经过频域积分处理的峭度指标趋势如图9所示,正常数据及退化数据的峭度指标均在3左右,且较为集中。同时,存在9个数据点明显偏离且与图6识别的劣质数据相吻合。因此,提出的指标能够较好地区分劣质数据与反映轴承状态的数据。 (a)零点漂移 (b)局部噪声 (c)正常信号 (d)故障信号图8 频域积分时域图Fig.8 Time domain diagram of frequencydomain integration 图9 频域积分后的峭度指标趋势图Fig.9 Trend chart of frequency domain integralkurtosis index 为了自适应获取劣质数据,采用统计学方法进行阈值选取。分别采用固定带宽核密度估计及本文提出的可自适应带宽核密度估计对指标进行统计分析,其中基于固定带宽估计的带宽为0.5。此外,对比分析采用基于四叉树分割算法的自适应带宽算法[16],分割的区域参数来自文献[16]的经验公式。采用95%置信区间进行阈值划分。 图10为不同方法对数据分布的估计结果。图10a中,统计的峭度指标主要集中在2左右,3种方法在[5,25]区间的高斯核密度估计分布较为接近。而在[5,25]区间中,提出的方法估计结果与频率分布直方图的更为接近。固定带宽估计方法无法兼顾不同稀疏程度的分布结果。相比于提出的方法,基于四叉树分割的自适应带宽的核密度估计在[5, 25]区间分布更为平滑,局部特性差,主要是由于其带宽在该区间普遍大于提出的方法。由于峭度指标不小于0,下边界为0,根据95%的置信区间制定上边界阈值,如表1所示。 (a)概率密度分布 (b)带宽 (c)累积概率图10 不同方法对数据分布的统计Fig.10 Data distribution estimation of different methods 表1 阈值设定(95%置信区间) 根据表1给出的阈值设定,对原始数据频域积分峭度进行异常组识别,识别结果如图11所示。固定带宽及提出的方法均能有效识别劣质数据,而基于四叉树分割算法的核密度估计方法出现了一组漏判。值得注意的是,固定带宽核密度估计方法确定阈值与退化数据较为接近,极易误判。 图11 原始数据识别结果Fig.11 Identification results of original data 图12 轴承滚动体剥落Fig.12 Spalling of bearing rolling body 图13 劣质数据识别结果Fig.13 Identification results of poor quality data 采用同一测试台架,在相同测试工况下对相同型号的车桥进行振动状态监测。该试验的最终结果为轴承滚动体剥落,如图12所示。采用上述方法对监测数据进行数据质量评估,通过峭度指标及信号时域分析,发现采集的658组数据中的5组存在明显的质量问题。上述提出的阈值在劣质数据识别时的结果如图13所示。图13中,提出的方法准确识别了所有的劣质数据。固定带宽的核密度估计方法识别的阈值过小,导致374组后出现大量的误判问题。而基于四叉树分割算法的自适应核密度估计方法出现了1组漏判,而漏判的值与阈值较为接近。结合图10a可以发现,基于四叉树分割的方法在[5,25]区间估计的概率密度较为平滑,与条形图分布有所区别,推测分割区域参数选择不合理是导致基于四叉树分割算法出现漏判的原因[17]。采用混淆矩阵[19]的指标对结果进行评估,如图14所示,自适应核密度估计方法均有较好的估计效果,且在同型号设备劣质数据识别中具有较好的泛化能力。 图14 统计分析Fig.14 The statistical analysis (1)本文提出的频域积分峭度指标对旋转机械劣质监测数据具有较好的识别能力,尤其是对具有零点漂移的时序数据。 (2)提出了基于自适应带宽核密度估计的异常监测数据识别方法。相比于固定带宽的核密度估计以及基于四叉树分割算法的自适应核密度估计算法,提出的方法能够自适应地拟合监测指标的分布情况,采用95%置信区间能够很好地识别异常数据,且对同型号设备的异常数据识别具有较好的泛化能力。 (3)本文提出的基于统计分布的阈值制定方法依赖于数据分布的完备性,后续将进一步深入分析研究。
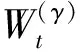
3 试验验证
3.1 试验条件及参数


3.2 指标提取

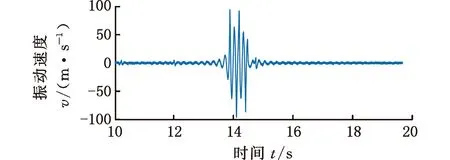




3.3 阈值制定
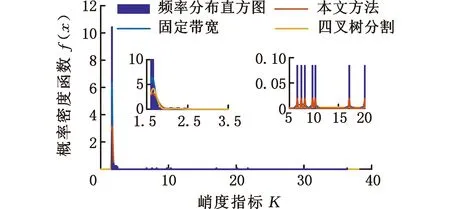

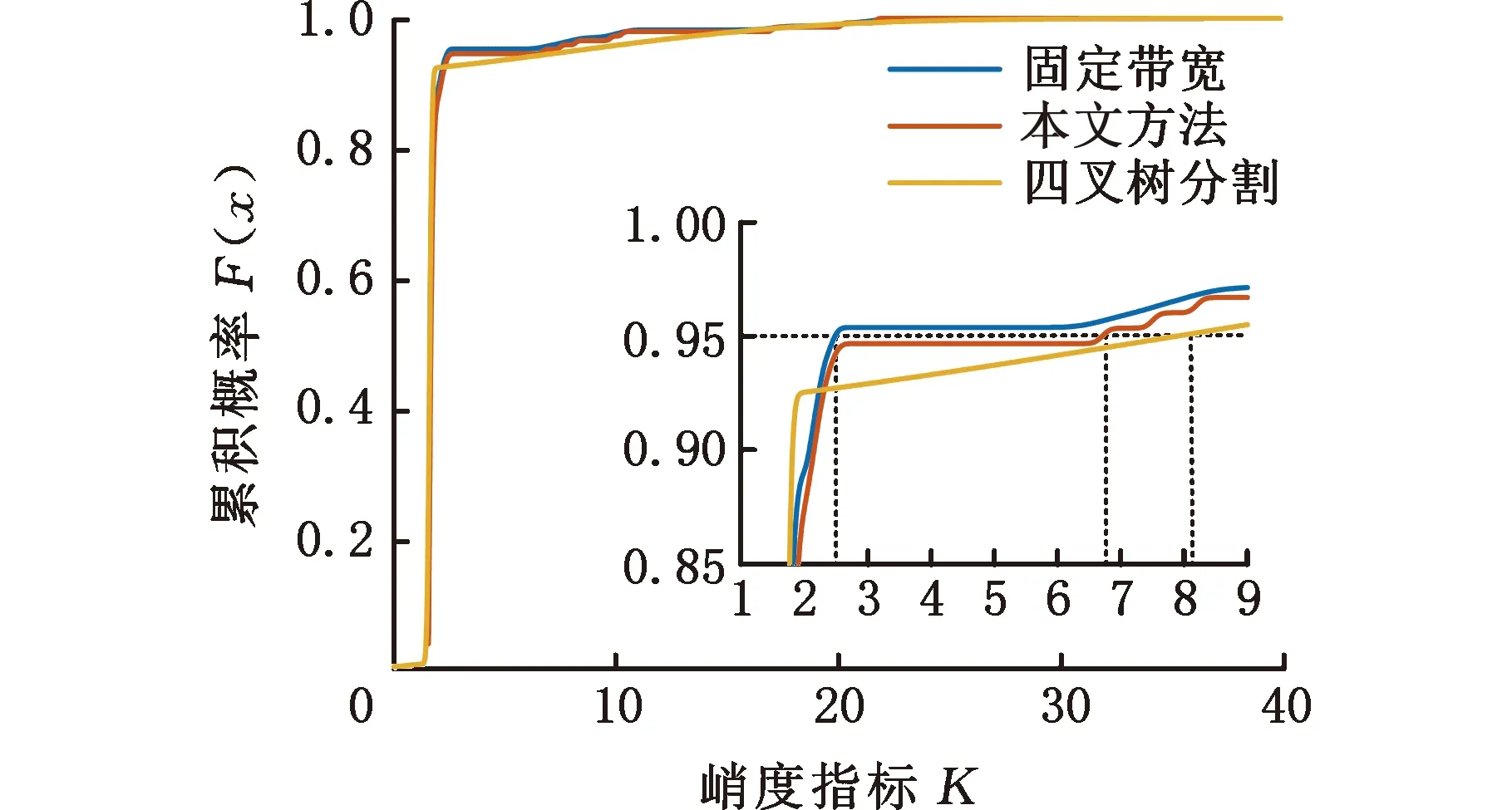


3.4 数据验证


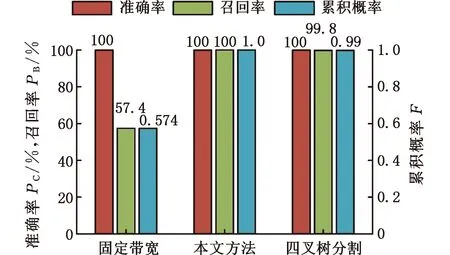
4 结论
