匹配和不匹配干扰共存时电液伺服系统预设性能渐近跟踪控制

董振乐 杨英浩 姚建勇 张 政 李阁强 王 帅

1.河南科技大学车辆与交通工程学院，洛阳，4710002.浙江大学流体动力与机电系统国家重点实验室，杭州，3100273.南京理工大学机械工程学院，南京，2100944.河南省机械装备先进制造协同创新中心，洛阳，471000

0 引言

电液伺服系统相比机电和气压系统具有功率质量比高、负载能力强等突出优势，在工业和国防领域有广泛应用[1-3]。随着装备性能不断升级，对电液伺服系统在服役过程中的运动/力精度要求愈发苛刻。对此，除需高性能的液压元件和系统集成设计作为支撑外，控制策略的需求也十分迫切，由于液压件研发周期长，优良的控制策略成为系统性能提升的关键途径。电液伺服系统存在诸多非线性环节和时变干扰，非线性环节有控制输入-负载流量非线性和负载压力-负载流量非线性等[4]，时变干扰则分为不匹配干扰(即不在控制通道内，如负载运动时所受环境外干扰、强密封下的难以精确建模的摩擦干扰等)和匹配干扰(即在控制通道内，如难以预测的外泄漏，不同工况下参数变化与状态耦合引起的干扰等)，这些均给控制策略的设计带来很大难度。

针对电液伺服系统非线性，相关学者通过对各类非线性环节进行更精细的建模或模型辨识，实现了较好的补偿效果，如余臻等[5]、YAO等[6]、HELIAN等[7]。而如何处理时变干扰成为现阶段电液伺服系统非线性控制策略研究的主要关注点。YAO等[8]提出融合反步设计和不连续映射的自适应鲁棒控制策略，同时处理了匹配干扰和不匹配干扰；GUAN等[9]针对含有非线性不确定参数的电液控制系统, 提出了一种滑模自适应控制方法，削弱了由于初始控制容积不确定引起的非线性不确定参数匹配干扰对控制性能的影响；YAO等[10-11]提出基于误差符号积分(RISE)的控制方法，先后实现了电液伺服系统在不匹配干扰或匹配干扰下的高精度控制，后续又提出自抗扰自适应控制方法[12]，实现了系统在匹配和不匹配常值干扰共存时的稳态渐近控制；张震阳等[13]提出采用扩张状态观测器(ESO)的估计匹配干扰，提高了系统跟踪精度。

上述研究均针对稳态性能进行控制设计，其最理想的理论结果是渐近稳定，即控制误差随时间理论上逐渐趋近于零，然而，当匹配和不匹配时变干扰共存时，尚未有文献获得渐近控制结果。此外，当系统运行初始位置和指令初始位置不一致时，或在某些短时动作场合(如模锻电液锤、液压弹射等)，瞬态性能(如超调量、收敛速度等)对系统运行质量十分重要，因此，将瞬态性能和稳态性能并重，才可确保系统高质量地输出运动或力，而现有研究鲜有将两者兼顾。董振乐等[14]基于预设性能函数[15]改善了系统瞬态控制性能，然而对于存在干扰时的稳态控制精度，并未获得最佳的理论结果，原因是电液伺服系统模型结构使得传统渐近稳定设计方法(如RISE和滑模等)很难融入预设性能函数，且无法同时处理匹配和不匹配干扰，甚至面临高增益反馈的风险，如何克服这个难题成为本研究的出发点。

综合以上考虑，本文针对电液伺服系统匹配和不匹配干扰共存的特点，兼顾瞬态性能和稳态性能需求，提出一种新型高精度控制策略。以电液位置伺服系统为例，建立了包含匹配和不匹配干扰的非线性数学模型，定义预设性能函数规划控制误差，并融合反步设计和采用干扰上界估计的连续渐近控制技术处理匹配和不匹配干扰，最终获得可预设的瞬态性能和渐近稳态性能，实现高精度跟踪控制。

1 系统建模

本文所考虑的电液位置伺服系统原理如图1所示，由伺服阀控制液压缸两腔流量进而控制两腔压力，实现对活塞杆伸出长度的控制，活塞杆外接负载，最终可实现负载执行件的位置调节。

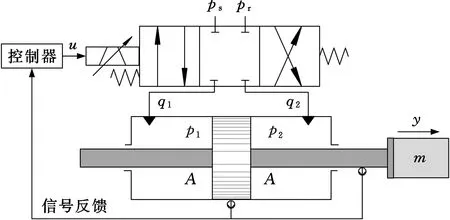
图1 电液伺服系统原理示意图Fig.1 The sketch of electro-hydraulic position servo system

根据牛顿第二定律，负载动力学方程为

(1)

pL=p1-p2

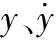
压力动态方程可由下式描述[4]：

(2)

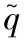
高性能伺服阀的频宽高达上百赫兹，其响应远高于整个伺服系统的响应，建模时可忽略伺服阀的动态，视输入电压u和伺服阀芯位移xv之间为比例环节，即xv=kuu。根据文献[4]可知负载流量qVL和伺服阀输入电压u的关系：

(3)

式中,kq为流量增益；Cd为伺服阀节流孔系数；w为伺服阀节流孔面积梯度；ρ为液压油密度；ps为系统供油压力，系统回油压力为零。

(4)

g2=4Aβe/Vtg3=4Ctβe/Vt

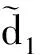
2 控制器设计

2.1 预设性能函数

定义位置跟踪误差e1=x1-x1d，假设因负载任务设定，跟踪误差需满足以下性能指标：

-δρ(t)0

(5)

(6)

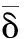
显然，式(5)和式(6)对跟踪误差e1作出了如下预设：-δρ0和δρ0分别预设了跟踪误差的最大下冲量和最大超调量，参数k预设了跟踪误差的收敛速度，ρ∞预设了跟踪误差的稳态收敛域。

进一步定义如下递增函数：

(7)

分析式(7)可知，根据递增函数S(z1)的性质，式(5)显然等价于e1(t)=ρ(t)S(z1)，且当z1有界时，式(7)始终成立。下面给出一个可用的函数S(z1)[15]:

(8)

为了便于后续推导，将S(z1)记为λ。

求式(8)反函数：

(9)

接下来基于转换误差z1设计最终控制器。

2.2 控制器设计

对式(9)求导，可得

(10)

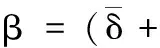
进一步可得

(11)

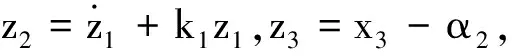
(12)

设计稳定函数α2为

(13)

式中，k2为正的可调反馈增益；α2a用于前馈补偿相应的系统动态函数和预设性能函数；α2s1为线性鲁棒稳定项。

将式(13)代入式(12)，可得

(14)

设计式(13)中的α2s2如下[16]:

(15)

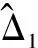
式(15)中α2s2显然是连续的，通过其实现对不匹配干扰的渐近抑制，证明过程随后给出。

同样，结合前文定义及式(4)，有

(16)

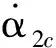
(17)

根据式(16)，最终控制器可设计为

(18)

式中,k3为正的可调反馈增益；ua用于前馈补偿相应的系统动态；us1为线性鲁棒稳定项。

将式(18)代入式(16)，可得

(19)

则可设计us2如下[16]：

(20)

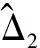
式(20)中us2显然是连续的，通过它实现对匹配干扰的渐近抑制，证明过程随后给出。

对于函数ε1(t)和ε2(t)，令其满足

(21)

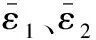
2.3 控制器性能

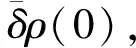
(1) 整个电液位置伺服闭环系统中所有信号都是有界的，即系统不会失稳，且位置控制误差具有式(5)、式(6)所预设的瞬态性能。

(2) 系统最终渐近稳定，即当时间t趋近于无穷时，位置误差e1趋近于零。

证明：详情扫描OSID二维码获得。

所提出的控制器总体框图见图2。

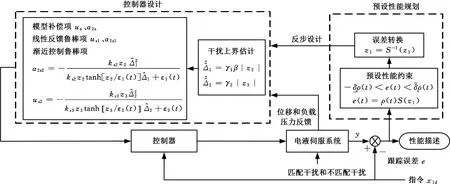
图2 控制器总体框图Fig.2 The overall block diagram of the controller

3 试验验证

图3所示为电液位置伺服系统试验平台，由机械底座、伺服阀(Moog G761-3003，流量19 L/min，频宽不小于120 Hz)、光栅尺(Heidenhain LC483，精度±5 μm)、压力传感器(MEAS US175-C00002-200BG，精度0.1 MPa)、液压缸组件(行程44 mm，有效作用面积904.78 mm2)和负载质量块(30 kg)组成，控制系统A/D卡采用研华PCI-1716，D/A卡采用研华PCI-1723，计数卡采用Heidenhain IK-220，基于LabWindows-CVI平台建立人机交互、运动监控和指令模块，采样时间0.5 ms。

图3 试验平台Fig.3 Experimental platform

为了充分验证所设计控制器的有效性，选取以下4种控制器进行对比试验：

(1)PID，即经典的比例-积分-微分控制，调试后的参数为kP=420，kI=120，kD=0。

(2)FLC，即反馈线性化控制，用于验证所建立数学模型对控制性能的补偿效果。基于系统模型(式(4))，该控制器的结构为

(22)

式中，μ1为位置控制误差；μ2、μ3为辅助设计误差；k1、k2、k3为正的反馈增益；ψ为稳定函数。

调试后，控制器各参数选取为：k1=300，k2=100，k3=0.0002。

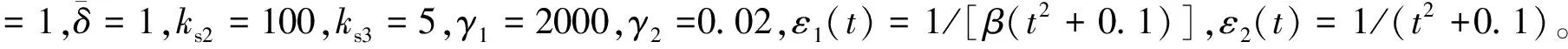
(4)PPC，即仅具有预设瞬态性能的控制器，可参考文献[14]，相比本文设计控制器，该控制器中不包含渐近稳定设计，即去掉式(15)的α2s2以及式(20)中u2s2。为了确保对比的有效性，控制器参数取值同PPAC。

3.1 试验工况一

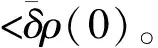
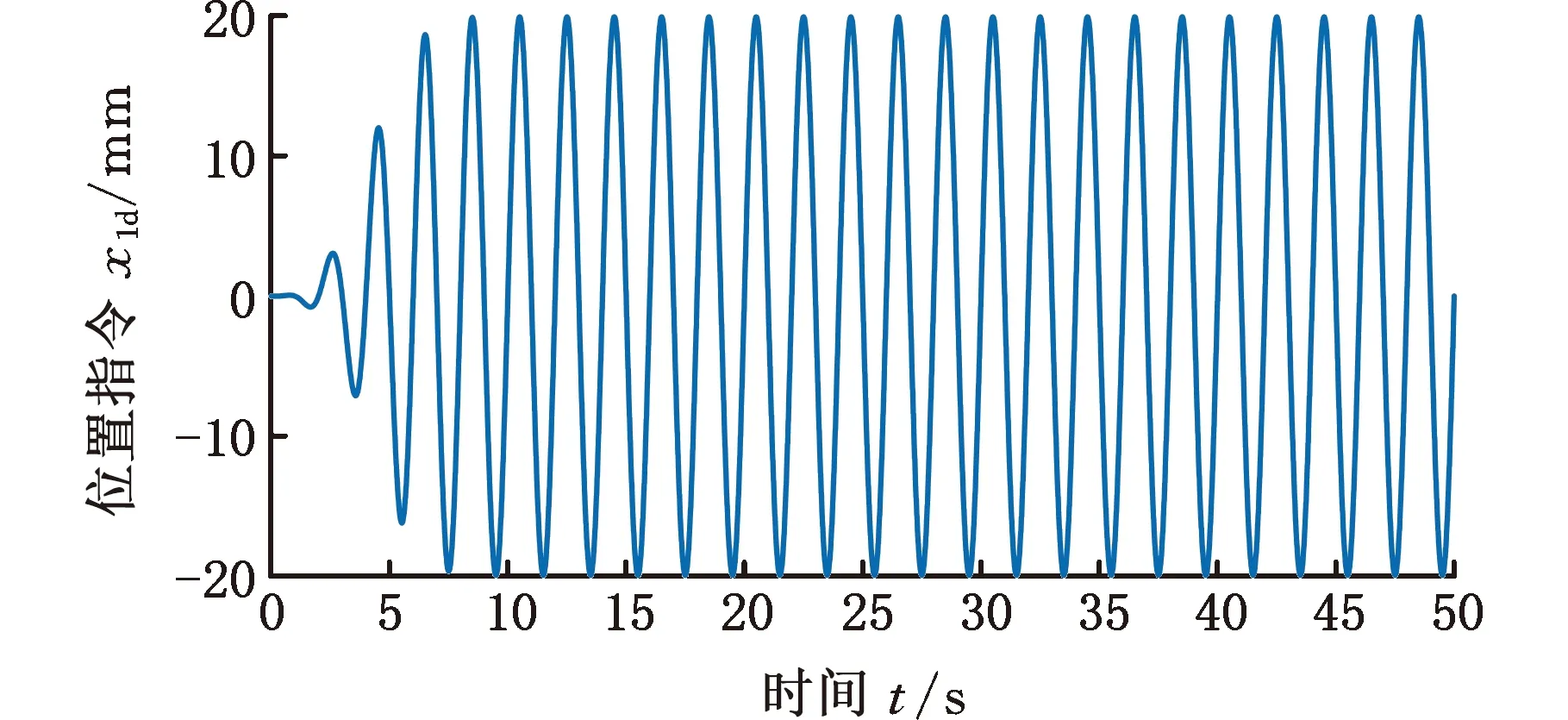
图4 工况一位置指令Fig.4 Command position for condition one

图5为4种控制器作用下的跟踪误差对比曲线，另外计算了前两个运动周期和最后两个运动周期的最大跟踪误差emax，如表1所示。显然，FLC控制器由于包含模型补偿成分，相比PID控制器，稳定阶段的最大跟踪误差由0.641mm减小至0.265 mm，而由于FLC控制器包含了系统参数信息，参数偏差导致其初始阶段最大跟踪误差相比于PID由0.035 mm增至0.058 mm。当控制器中加入预设性能函数后，在函数的规划作用下，PPC控制器初始阶段和稳态阶段的最大跟踪误差分别为0.027 mm和0.112 mm，相比于PID和FLC控制器，初始阶段跟踪精度提高均超22.9%，稳态阶段跟踪精度提高均超过57.73%。在控制器中加入基于干扰上界估计的连续渐近控制技术(即本文提出的PPAC控制器)，初始阶段和稳态阶段的最大跟踪误差分别为0.024 mm和0.067 mm，相比PPC初始阶段跟踪精度提高约11.1%，稳态阶段跟踪精度提高约40.2%，且随着时间推移，控制误差仍有下降趋势。图6给出了所选取预设性能函数与PPC、PPAC控制误差的对照效果，可知控制误差始终处于预设函数界内。另外图6给出了匹配干扰和不匹配干扰的上界估计曲线，证明两者是共存的，估计算法的收敛效果较好，在15 s左右趋于稳定，与之对应，随着干扰上界估计的收敛，图5中PPAC的稳态阶段控制误差较初始阶段控制误差明显减小。

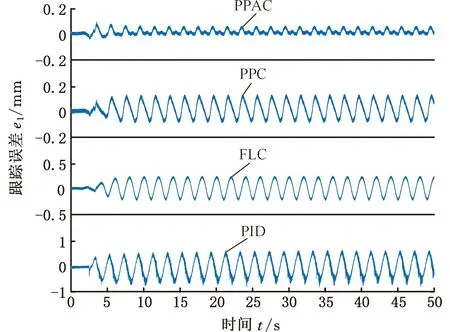
图5 工况一跟踪误差对比Fig.5 Comparison of tracking errors for condition one

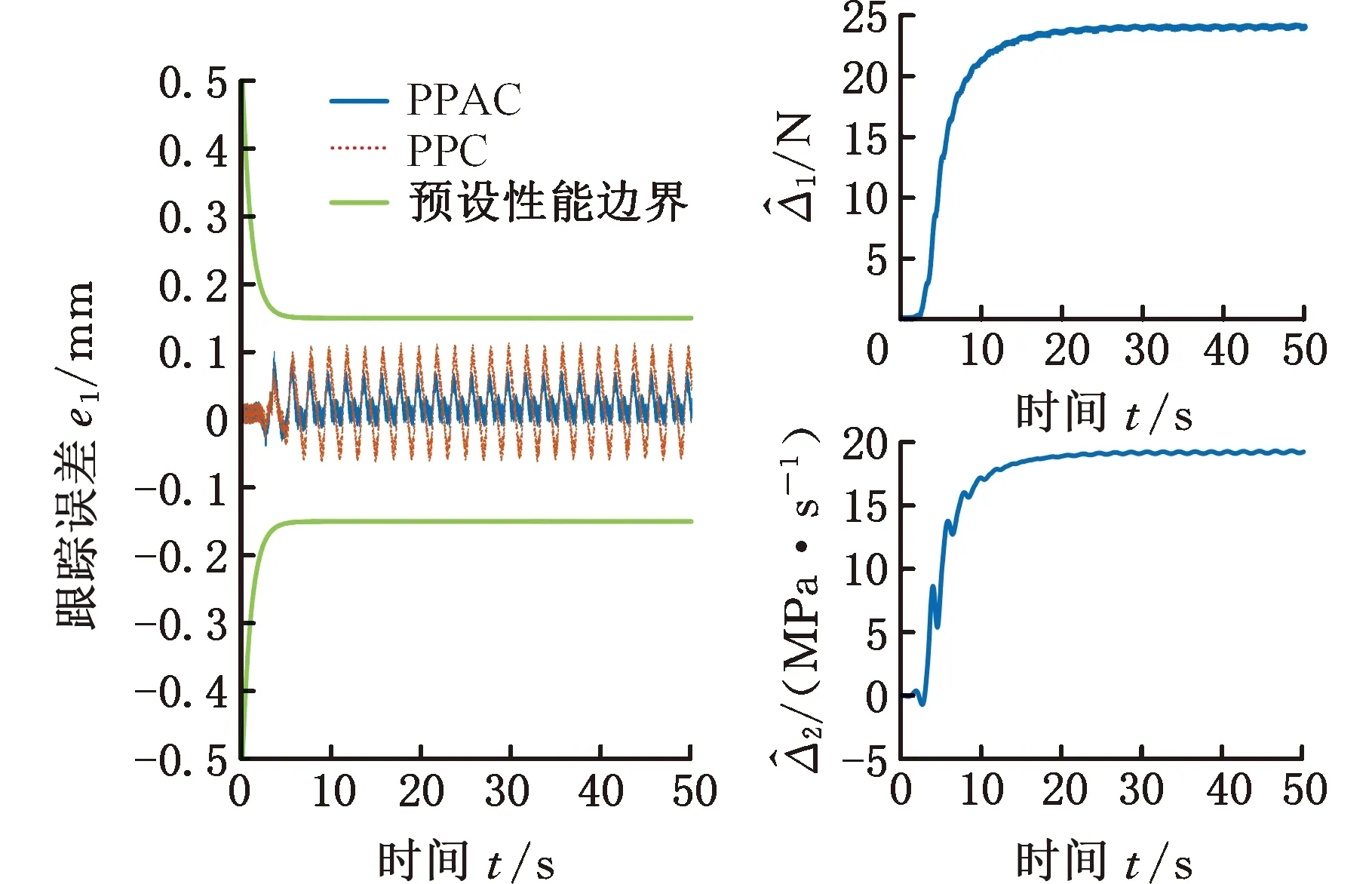
图6 工况一预设性能效果和Fig.6 Effect of prescribed performance for condition

表 1 工况一最大跟踪误差emax

3.2 试验工况二

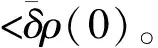
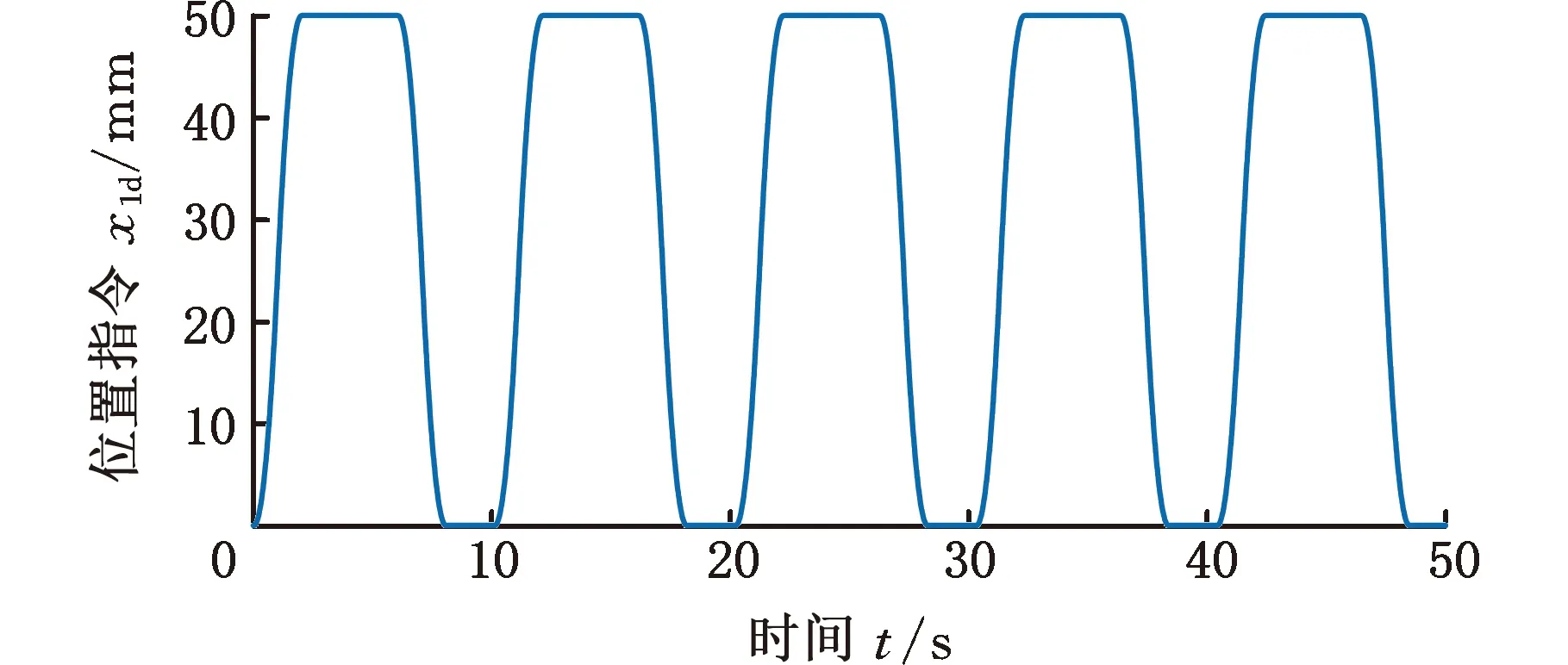
图7 工况二位置指令Fig.7 Command position for condition two

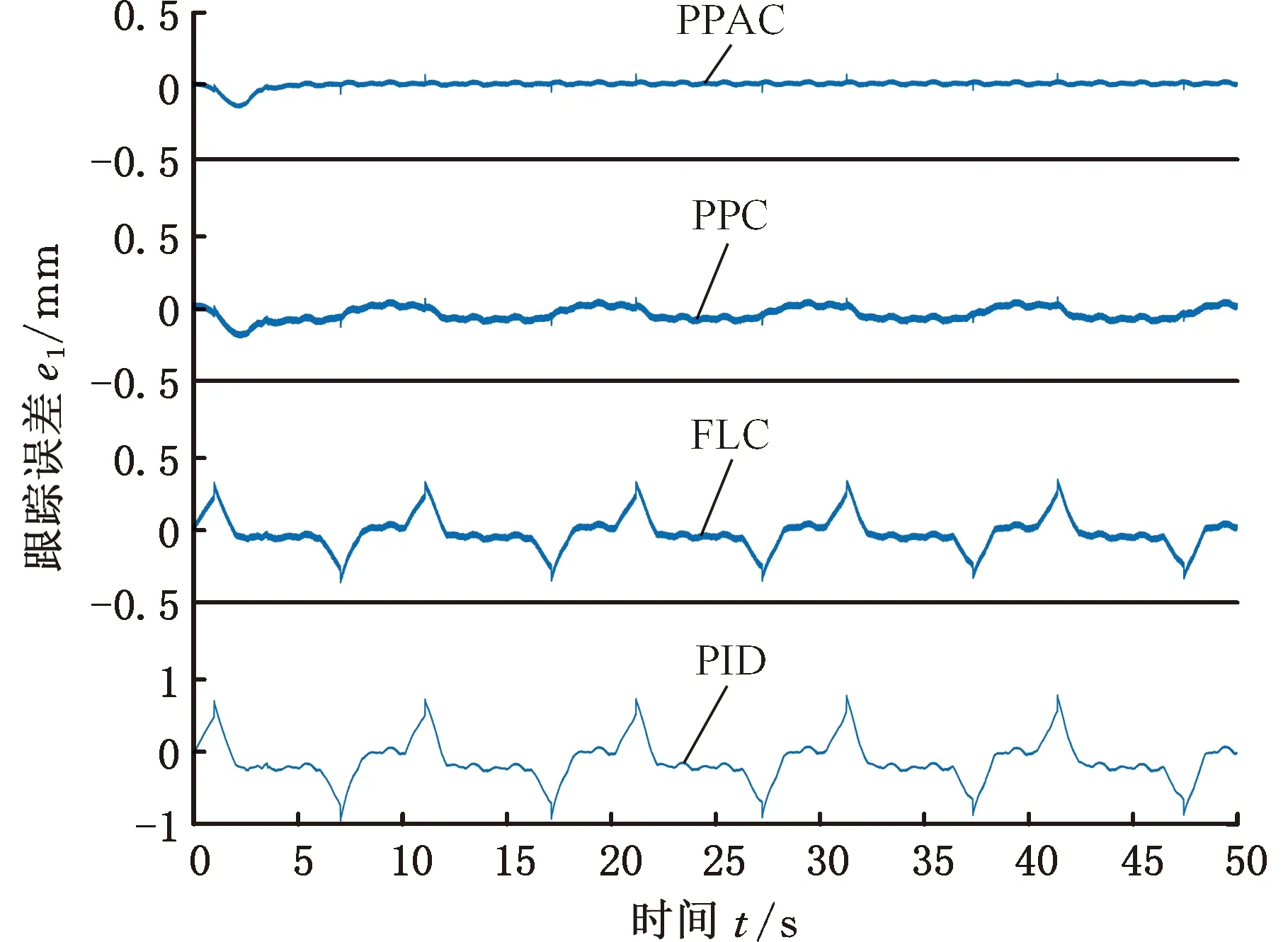
图8 工况二跟踪误差对比Fig.8 Comparison of tracking errors for condition two

图8为4种控制器作用下的跟踪误差对比曲线，另外计算了第一个运动周期和最后一个运动周期的最大跟踪误差emax，如表2所示(在工况一中，由于位置指令为经过光滑处理的正弦指令，初始阶段较为平缓，因此选取两个周期的数据进行对比)。显然，FLC控制器相比于PID控制器，初始阶段和稳定阶段的最大跟踪误差分别由0.882 mm和0.932 mm减小至0.362 mm和0.354 mm。PPC控制器初始阶段和稳态阶段的最大跟踪误差分别为0.152 mm和0.149 mm，相比于PID和FLC控制器，初始阶段跟踪精度提高均超58%，稳态阶段跟踪精度提高均超57.9%。PPAC初始阶段和稳态阶段的最大跟踪误差分别为0.147 mm和0.085 mm，相比PPC初始阶段跟踪精度提高约3.2%，稳态阶段跟踪精度提高约42.9%。图9给出所预设性能函数与PPC、PPAC控制误差的对照效果，可知控制误差始终处于预设函数界内。另外图9给出了工况二下匹配干扰和不匹配干扰的估计曲线，收敛效果较好，在6 s左右趋于稳定，与图8中PPAC的控制误差收敛趋势基本一致。

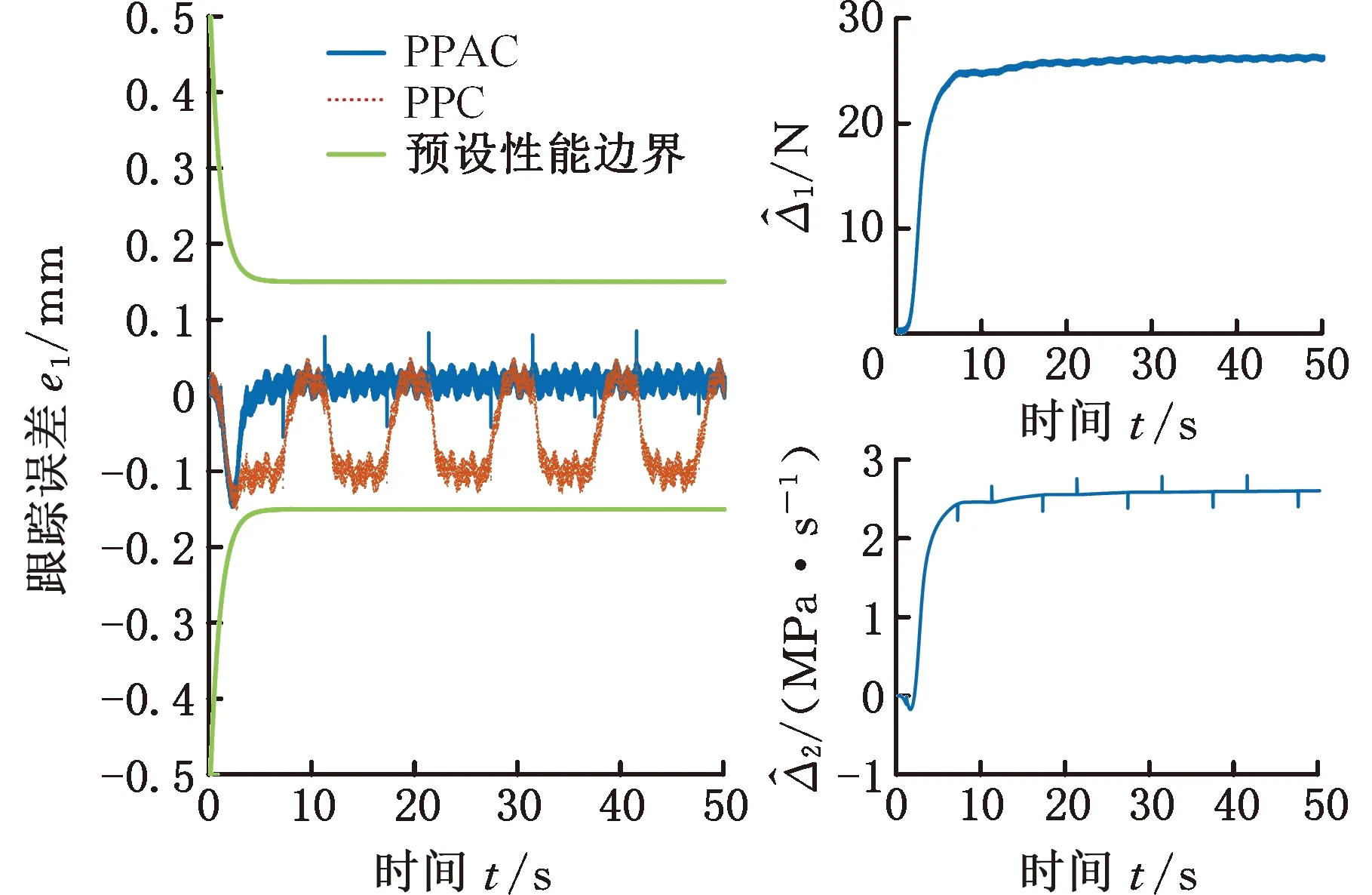
图9 工况二预设性能效果和Fig.9 Effect of prescribed performance for condition

表2 工况二最大跟踪误差emax

以上两种不同位置指令的跟踪试验均验证了在本文所设计控制器的作用下，电液伺服系统具有较好的瞬态和稳态性能，通过对比4个控制器在初始阶段和稳态阶段最大跟踪误差，表明预设性能函数的引入可明显改善瞬态性能，而基于干扰上界估计的连续渐近控制技术可进一步提升稳态阶段控制性能。

4 结论

(1)本文提出了一种融合预设性能函数和基于干扰上界估计的连续渐近控制技术的电液伺服系统新型高精度控制策略，通过Lyapunov稳定性分析证明了控制器具有理论可预设瞬态性能和渐近稳态性能。

(2)选取了PID控制、反馈线性化控制和预设性能控制作为对比，通过两种位置指令工况的跟踪试验，验证了匹配干扰和不匹配干扰是共存的，而所提出控制器可很好地抑制匹配和不匹配干扰，在两种试验工况中，所设计控制器相比传统PID控制和反馈线性化控制，初始阶段跟踪精度提高均超22.9%，相比于仅引入预设性能函数的控制器，稳态阶段跟踪精度提高超42.9%。