基于LS-DYNA 的45号钢铣削SPH 算法仿真分析

徐晴，仲梁维

（200093 上海市 上海理工大学 机械工程学院）

0 引言

金属切削加工是一种利用刀具从毛坯或半成品上切去多余材料来获得符合技术要求的零件或半成品的加工技术[1]。切削过程是一个涉及到多学科的复杂工艺过程[2]，切削速度、进给速度以及切削深度等参数均会对切削作用产生明显影响。随着计算机仿真技术的发展，切削过程中的重要参数如切削力可以计算得到，能节省实验成本。本文运用LS-DYNA 的SPH 方法分析45 号钢的铣削过程，得出45 号钢在切削过程中的变形及切屑的形成过程，并控制切削参数，得出切削力受切削速度、进给速度及切削深度变化的影响。

1 计算方法

SPH 算法（光滑粒子方法）是一种无网格算法。SPH 算法基本原理是：把一个几何体离散成许多具有一定体积和质量的粒子，将单元化作粒子，通过某一时刻临域内所有粒子插值求和，可求出该时刻空间内任何一点的物理量以得到连续场的近似[3]，将连续介质动力学的守恒定律由微分方程形式转换成积分形式，从而转换为求和来获得解。SPH 法中，质点近似函数定义为

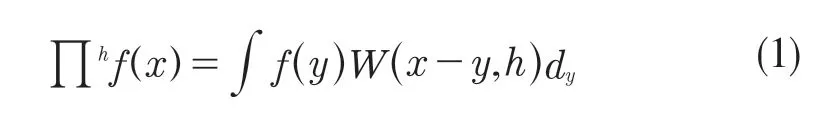
式中：W——核函数(插值核)，使用辅助函数θ进行定义：

式中：d——空间维度；h——光滑长度；辅助函数θ可由式（3）表示：

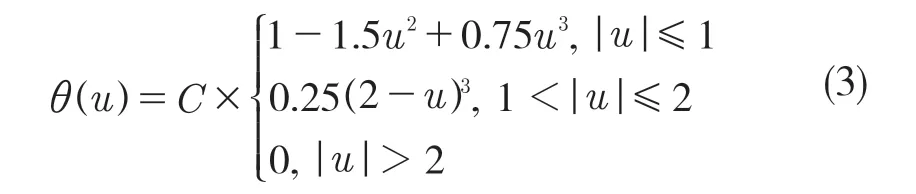
式中：C——规一化常量[4]。

有限元分析中，单元形状会很大程度上影响计算结果，因为如果变形过大，会造成网格严重畸变，导致矩阵岐意，计算结果的精度会严重下降，甚至求解失败。SPH 方法不存在网格畸变问题，适合求解破坏类型和极度变形的问题，所以SPH 方法在数值分析领域应用更加广泛。

2 切屑形成仿真

2.1 几何模型

在LS-PrePost 中建立模型，运用SPH 功能创建一45 号钢待加工工件模型。工件为一长方体金属块，长为10 mm，宽为5 mm，高为5 mm。刀具为实体模型，建立好的模型如图1 所示。

图1 金属切削模型Fig.1 Metal cutting model

2.2 材料模型

刀具为刚性体，选取Rigid 模型，刀具材料为硬质合金。金属工件采用Johnson-Cook 材料模型。Johnson-Cook 材料模型是一个能反映应变率强化效应和温升软化效应的理想刚塑性强化模型，本构方程如下：

式中：A，B，n，C，m——材料参数；σ——vonMises 流动应力；ε——等效塑性应变；——相对等效塑性应变率；——等效塑性应变率；——准静态应变率，取=0.001 s-1；Tm——材料熔点；Tr——室温，取20 ℃。以45 号钢为例，其材料属性见表1。

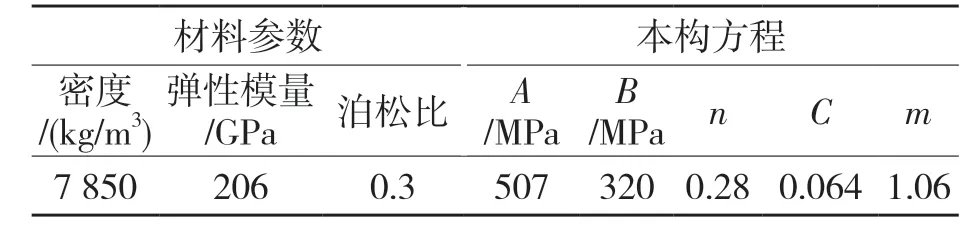
表1 Johnson-Cook 模型材料参数及本构方程Tab.1 Material parameters and constitutive equations of Johnson-Cook model

Johnson-Cook 失效准则为

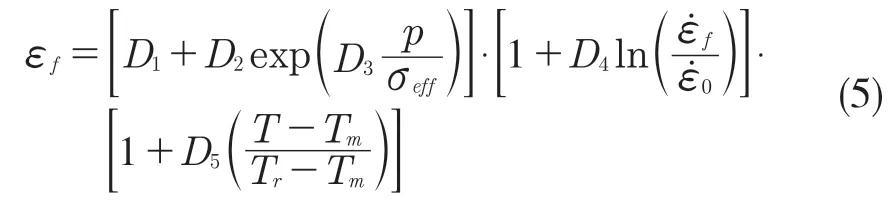
表2 Johnson-Cook 失效准则Tab.2 Johnson-Cook failure criteria

2.3 边界条件加载

切削加工时，金属块被夹具固定在工作台上，刀具沿水平方向作直线运动，因此在模拟切削加工时对金属块SPH 模型下部节点施加全自由度约束，对刀具的旋转自由度全部约束，y，z方向的移动自由度也施加约束，使刀具只能在x方向作直线运动，并对刀具施加沿x轴负方向大小为5 m/s 的速度。刀具形状的基本参数为：前角γ0=11°，后角α0=10°，切削厚度为1.5 mm。刀具和金属之间接触采用AUTOMATIC_NODES_TO_SURFACE，摩擦系数为0.2。

2.4 求解结果分析

（1）塑性变形阶段。如图2 所示，切削开始后，刀尖和金属块发生接触并挤压金属块，上层SPH 粒子发生位移，此区域等效应力最大，可知金属块和刀尖接触区域发生塑性变形。

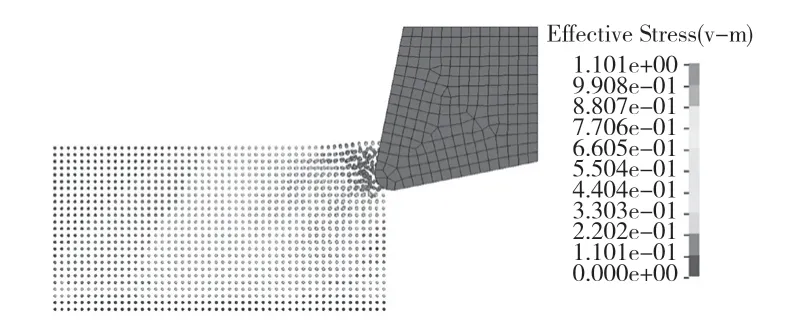
图2 塑性变形阶段Fig.2 Plastic deformation stage

（2）剪切滑移阶段。如图3 所示，刀具进一步向左运动，刀刃与金属之间的作用力变大，材料受到进一步的挤压，当内部应力达到材料的屈服强度时，就发生剪切滑移，表现为上部的SPH 粒子脱离金属块本体。

图3 剪切滑移阶段Fig.3 Shear slip stage

（3）切屑形成阶段。如图4 所示，刀具继续前进，更多的粒子脱离金属本体，组成条状物。滑移出的材料不断流出，并在刀具的挤压下产生塑性变形形成切屑。

图4 切屑形成阶段Fig.4 Chip formation stage

2.5 切削力及最大等效应力

如图5 所示，切削力与时间的关系为：当刀尖和金属接触时，切削力迅速增大，达到顶峰值9.8 kN，此时已达到金属工件的屈服应力，材料发生剪切滑移，切屑产生，切削力在一定范围内波动，约为8 kN；金属切削过程快结束时，切削力逐渐减小，到切屑完全和金属本体脱离时减小到零。最大等效应力如图6 所示，在切削过程中保持在1 100 MPa 左右，到切屑分离时有所回落。

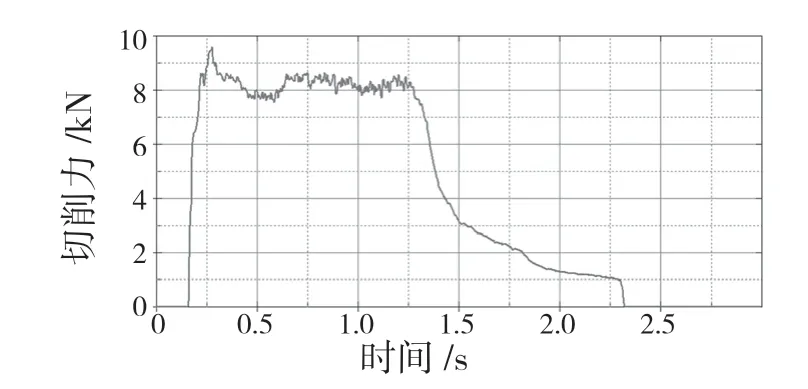
图5 切削力曲线Fig.5 Cutting force curve

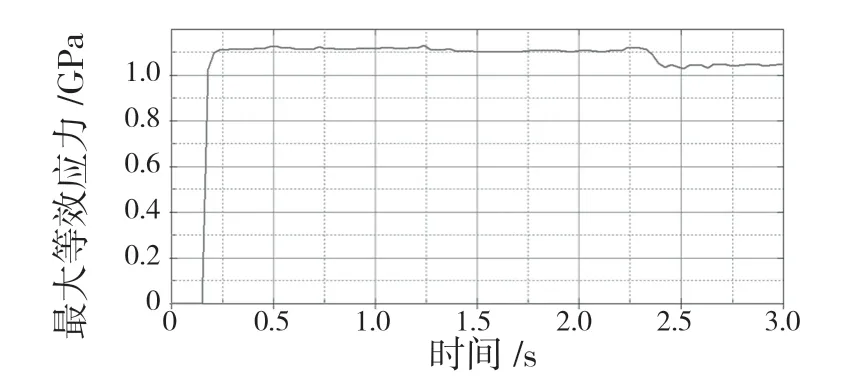
图6 最大等效应力曲线Fig.6 Maximum equivalent stress curve

3 铣削仿真分析

3.1 铣削参数

通过上述分析，证明SPH 方法仿真金属切削过程的可行性。以下验证不同切削参数对切削力的影响[6-7]。图7 是一个四刃铣刀模型，直径为10 mm，为简化计算，保留四刃铣刀头部。新建一45 号钢待加工工件模型，为一长16 mm，宽8 mm，高8mm 的长方体金属块。切削速度设为1 200 r/min，进给速度设为2 m/s，切削深度设为1 mm。铣削模型如图8 所示。

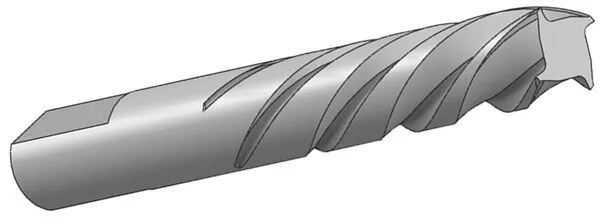
图7 四刃铣刀模型Fig.7 Four-edge milling cutter model

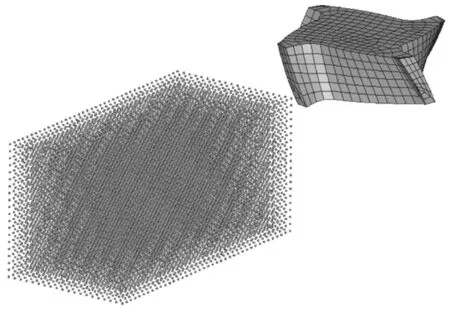
图8 铣削模型Fig.8 Milling model

3.2 铣削仿真结果分析

图9、图10 为切削结果，最大应力集中在主切削刃和金属接触的部位。切削力是周期性函数，如图11 所示，周期最高峰值超过1.4 kN，有多个高峰值在1.3 kN 附近，有8 个峰值超过1.2 kN。最大等效应力如图12 所示，在切削过程中大致在900 MPa 至1 200 MPa 范围内波动。

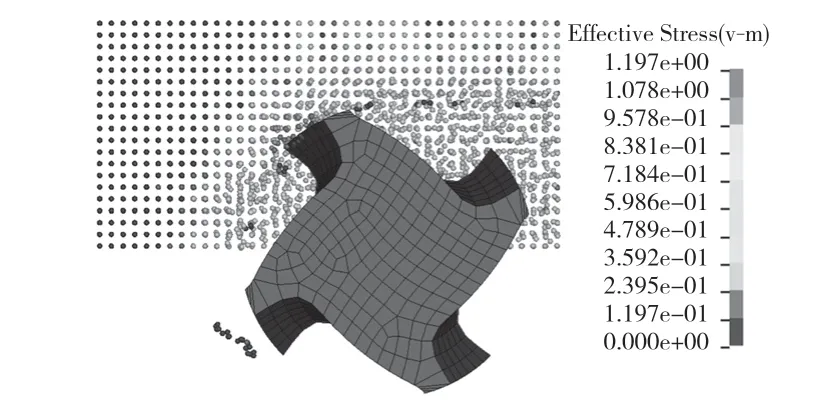
图9 铣削过程中Fig.9 During milling process

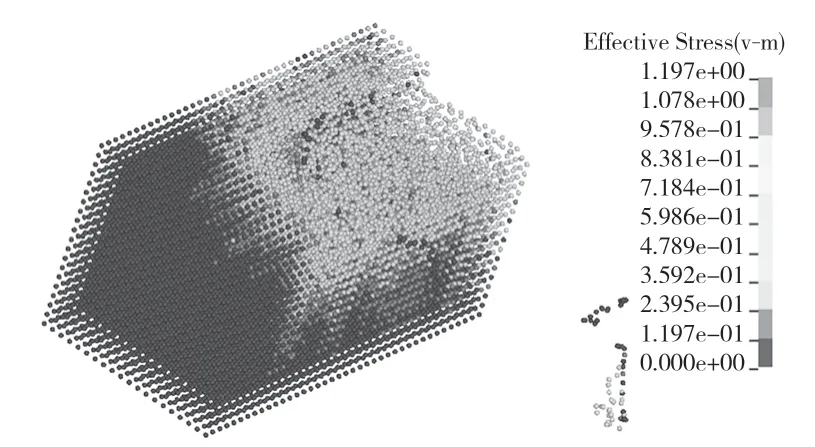
图10 铣削后的金属Fig.10 Milled metal

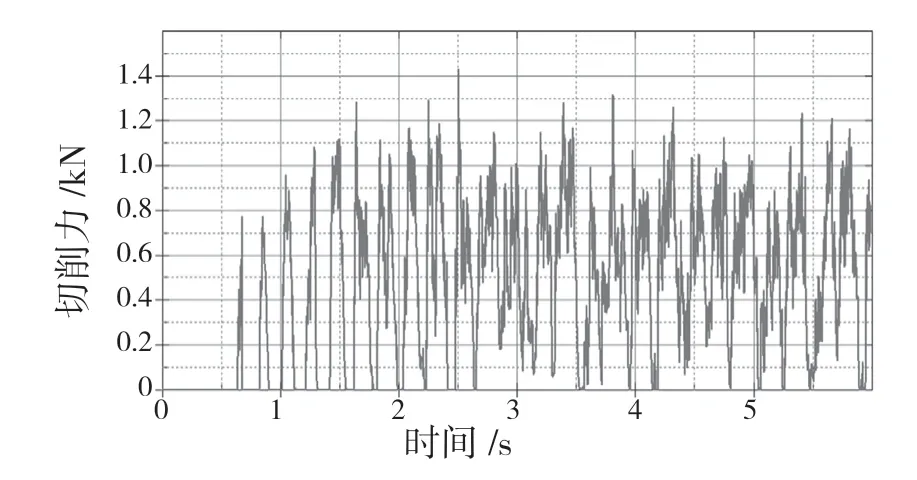
图11 铣削切削力曲线Fig.11 Cutting force curve of milling

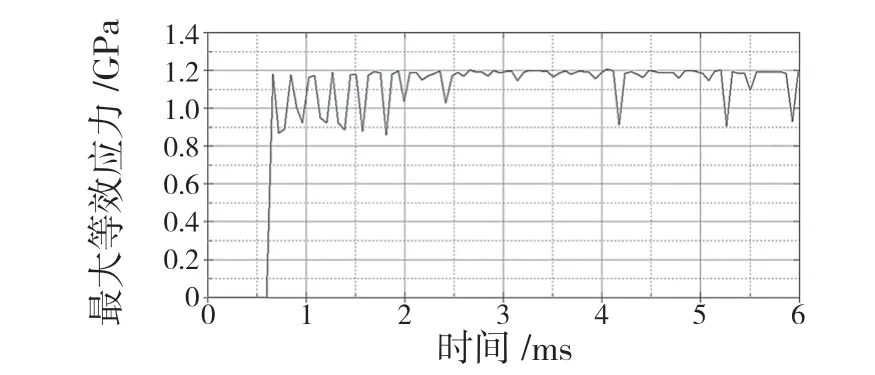
图12 铣削最大等效应力曲线Fig.12 Milling maximum equivalent stress curve

3.3 切削力经验公式

主切削力、进给抗力的车削三要素经验公式为

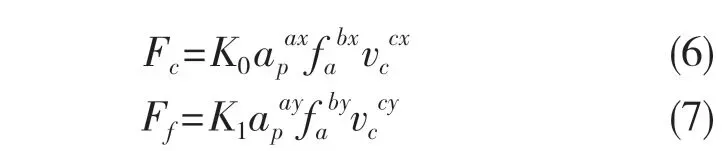
式中：Fc——主切削力；Ff——进给抗力；ap——切削深度；fa——进给量；vc——切削速度；K0，K1——系数；ax，bx，cx，ay，by，cy——指数。经验公式表明：一般来说，在切削速度较低的情况下，切削力随转速的增加而升高，但达到某一临界速度值后，随着转速继续增大，切削力反而下降；切削力与进给量呈正相关趋势，会随着进给量的增大而增大；切削深度与切削力也呈正相关趋势。

3.4 切削速度对切削力影响

将切削速度设置为1 800 r/min，得到切削力与时间的关系曲线如图13 所示。切削力的最高峰值约为1.3 kN，有4 个峰值超过1.2 kN，可知切削速度增大，切削力有所减小。

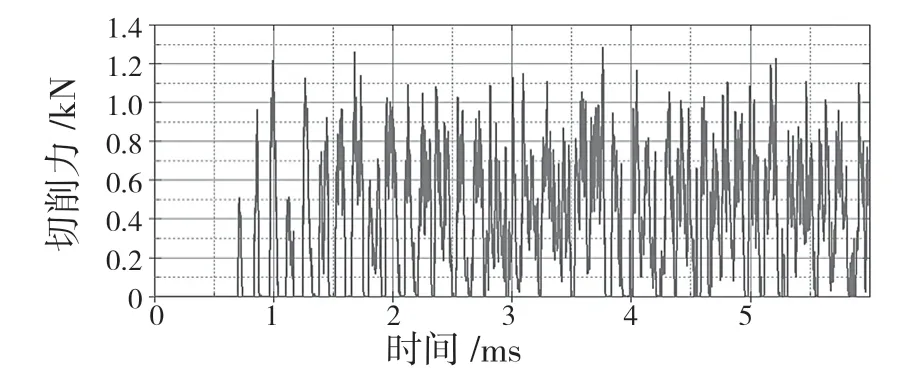
图13 增大切削速度的铣削切削力曲线Fig.13 Milling force curve with increasing cutting speed

3.5 进给速度对切削力影响

将进给速度设置成4 m/s，运行时间则减半为3 ms，如图14 所示。切削力的最高峰值达到1.75 kN 左右，因此若进给速度增大，切削力随之增大，和经验公式吻合。

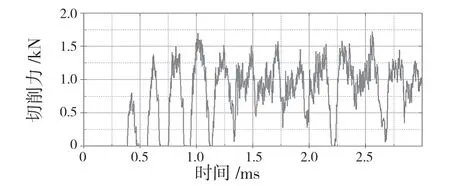
图14 增大进给速度的铣削切削力曲线Fig.14 Milling force curve with increasing feed speed

3.6 切削深度对切削力影响

将切削深度设置为2 mm，切削力与时间的关系曲线如图15 所示。切削力的最高峰值达到2.2 kN 附近，随切削深度增加，切削力增大。切削深度对切削力的影响更为明显。

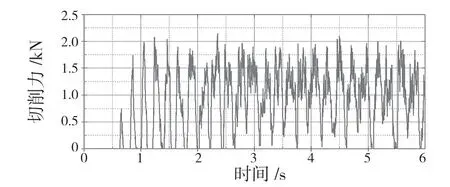
图15 增大切削深度的铣削切削力曲线Fig.15 Milling force curve with increasing cutting depth

4 结论

（1）运用SPH 无网格算法来仿真45 号钢铣削加工过程，得出起初金属材料发生塑性变形，之后材料发生部分剪切滑移成切屑，最终切屑与金属分离。

（2）开始切削时，金属和刀具接触，切削力迅速增大至最值，然后小幅减少，在切削过程中保持在一定范围内变动，直至切屑与金属体完全分离减小到零。

（3）控制不同铣削参数进行仿真，得出到一定切削速度后，切削力会随着切削速度的增大而减少，随进给速度、切削深度的增大而增大，且随切削深度增大得更明显。