I 型裂纹应力强度因子的有限元计算方法

李磅磅，邹志鉴

（200093 上海市 上海理工大学 机械工程学院）

0 引言

由于材料自身缺陷或加工过程中造成损伤，结构内部不可避免会存在微裂纹，在一定条件下微裂纹会不断扩展、积聚，最终造成材料断裂失效[1]。裂纹扩展导致的低应力断裂是造成各种结构、零部件失效及工程中各类重大事故的根源。在断裂力学中，应力强度因子KI是判断含裂纹结构的断裂和计算裂纹扩展速率的重要判据[2]。应力强度因子的计算方法有解析法、有限元法、权函数法等。有限元法具有强大的建模能力和计算能力，可以解决多种边界条件下的复杂问题，并能获得较高的精度，已成为确定应力强度因子的有效方法[3]。

本文以三点弯曲试样为研究对象，使用ABAQUS 建立有限元模型，分别采用位移外推法、应力外推法、虚拟裂纹闭合法计算I 型裂纹的应力强度因子KI，与试样的解析解进行比较分析，并且研究了载荷P、裂纹长度a及试样厚度B对I 型裂纹应力强度因子的影响。

1 计算方法

1.1 位移外推法

根据I 型裂纹尖端附近的位移公式[4]，有

用有限元软件求出位移ui后，代入式（1），即可求出应力强度因子KI。令θ=π，代入裂纹张开位移值ν（r，π）得到KI计算公式为

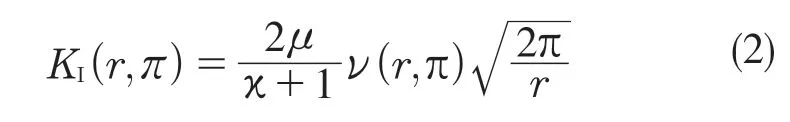
由于式（2）保留了r的奇异项，只在（r→0）时获得准确结果。但r太靠近裂纹时，常规单元无法正确反映裂纹尖端的奇异性，反而影响有限元的计算结果。构造数据对（ri，KIi）绘制曲线，使用外推法拟合数据点[5]，拟合直线的截距，即为应力强度因子：

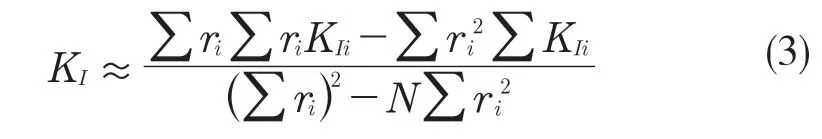
1.2 应力外推法

根据I 型裂纹尖端附近的应力公式[4]，有

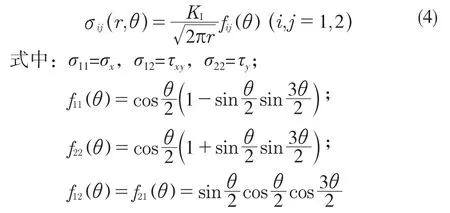
用有限元软件求出应力σij，代入式（4），即可求出应力强度因子KI。令θ=0，代入裂纹线上应力值σy（r，0）得到KI为

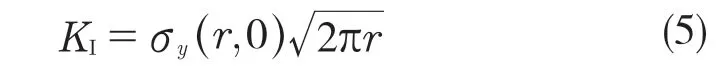
与位移外推法相同，求出不同r处的应力，计算得到相应的应力强度因子KIi，绘制曲线，通过外推法拟合，截距即为应力强度因子KI。

1.3 虚拟裂纹闭合法

虚拟裂纹闭合法是根据Irwin 应变能释放率理论提出的[6-8]，该理论认为裂纹扩展中释放的能量等于闭合裂纹所需要的能量。如图1 所示，设裂纹初始长度为a，扩展增量为Δa，根据Irwin 提出的裂纹闭合积分法，I 型裂纹应变能释放率可表达为

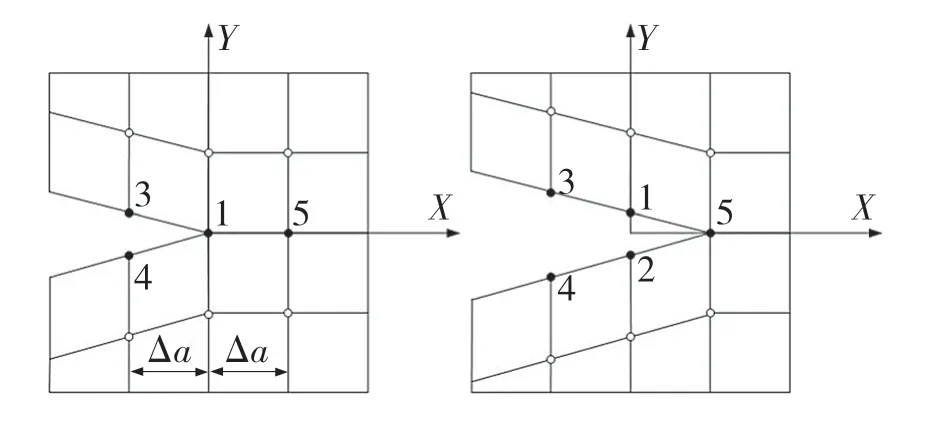
图1 虚拟裂纹闭合法示意图Fig.1 Schematic diagram of virtual crack closing method

式中：B——裂纹体板厚；σy y——沿着闭合裂纹面上的法向应力；Δv——闭合裂纹张开时上下裂纹面的相对位移分量。

有限元分析中，根据虚拟裂纹扩展原理，裂纹向前扩展时应力所做总功等于裂纹尖端节点力在该节点位移上所做的功，即

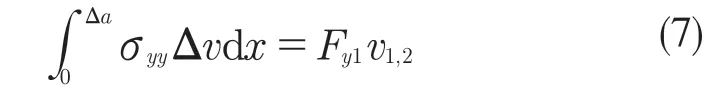
式中：Fy1——裂纹扩展前节点1 上y方向的节点力；v1,2——裂纹扩展后节点1、2 间y方向的节点位移。从而

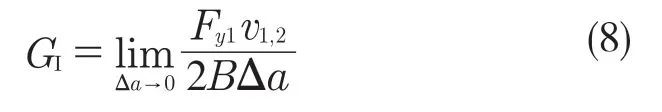
虚拟裂纹闭合技术假设裂纹扩展一个小量Δa后，裂纹尖端的应力场、位移场与扩展前相比保持不变。裂纹扩展前，节点3、4 的位移v3,4近似等于裂纹扩展后的节点1、2 位移v1,2，且网格扩展增量足够小，所以式（8）可表示为

应变能释放率与应力强度因子的关系[5]为

2 模型建立与验证

本文采用的三点弯曲试样参考GB/T 4161-2007《金属材料 平面应变断裂韧度KIC试验方法》中尺寸比例要求。如图2 所示，宽度W=40 mm，厚度B=20 mm，跨距S=160 mm，试件总长L=200 mm，裂纹长度a=20 mm。材料属性为：弹性模量E=2×105MPa，泊松比v=0.3；载荷P=200 N。

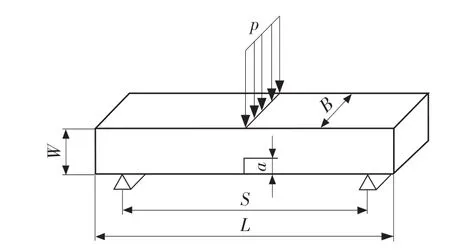
图2 三点弯曲试样Fig.2 Three-point bending specimen

三点弯曲试样为对称模型，在ABAQUS 环境中只需建立右侧1/2 模型进行仿真分析，Part 中建立shell 模型，选择planar 类型，绘制宽度40 mm，半长100 mm 的试样；在界面属性中，添加平面厚度20 mm；采用CPS4R 单元划分网格，网格长度0.5 mm。建立模型后生成inp 文件，修改inp 文件输出相关裂纹节点的应力、位移及节点力。使用节点位移外推法、单元应力外推法、虚拟裂纹闭合法计算I 型裂纹应力强度因子。

根据GB/T 4161-2007 的规定，三点弯曲试样的应力强度因子计算表达式[9]为

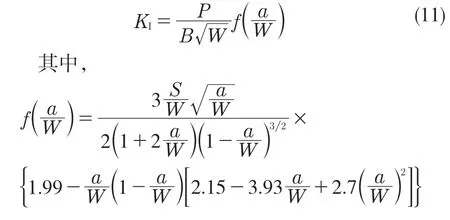
经仿真与计算，位移外推法、应力外推法、虚拟裂纹闭合法与解析法得到的计算结果分别为17.145 0，16.536 4，16.715 1，16.778 9 MPa·mm1/2，相对误差分别为2.18%，-1.44%和-0.38%，表明3 种有限元方法都可以准确计算应力强度因子KI值。

3 模型参数分析

应力强度因子的值与试样的几何尺寸、裂纹长度及载荷大小有关，为研究试样厚度B，裂纹长度a及载荷P对应力强度因子的影响，修改inp 文件，计算不同条件下的应力强度因子，并进行比较分析。

表1—表4 为不同条件下应力强度因子计算结果对比，图3 为变化趋势图。

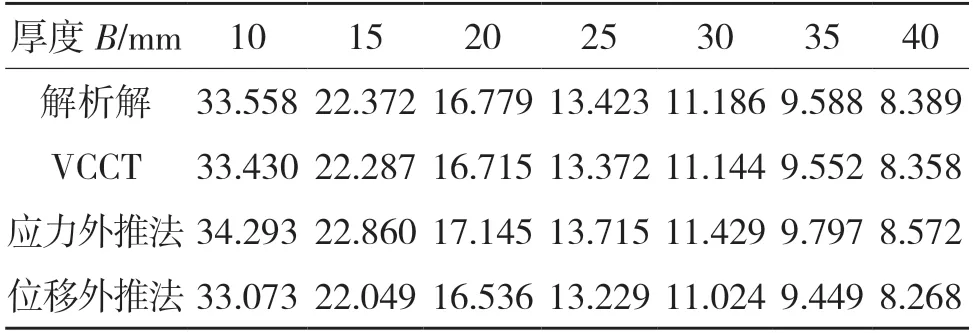
表1 不同试样厚度时KI 的值Tab.1 KI values at different sample thicknesses

由表1 和图3（a）可知，随试样厚度的增加，应力强度因子KI越来越小，且减小的趋势越来越缓慢。3 种有限元法的结果与解析解一致性较好，误差分别为-0.38%、2.18%和-1.45%，由式（11）可知，KI与B成反比关系，曲线变化符合理论结果。由图3（b）可知，KI随着载荷的增大而增大,有限元法与解析解呈线性增长，斜率近乎相同。根据表2 计算知，VCCT、应力外推法和位移外推法的误差分别为-0.38%、2.17%和-1.44%。

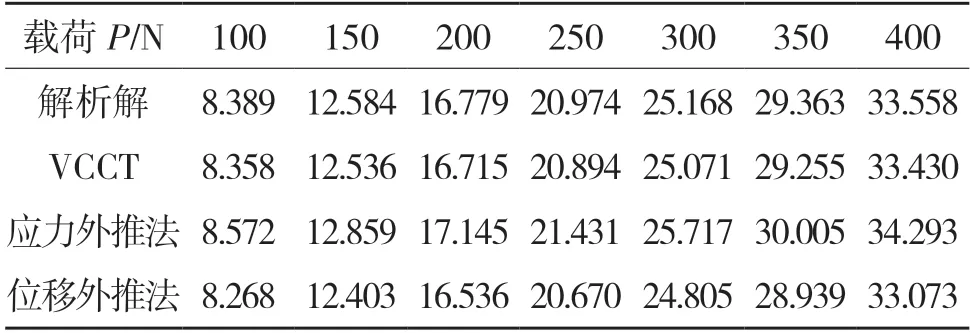
表2 不同载荷时KI 的值Tab.2 KI values at different loads

不同裂纹长度时的应力强度因子KI如表3 和图3（c）所示。随裂纹长度的增加，应力强度因子KI随之增加，增长速率变快。当a/W＜0.6 时，应力强度因子KI增长速度较为缓慢。应力外推法的结果整体大于解析解，位移外推法的结果整体小于解析解，VCCT 的结果误差相对更小。

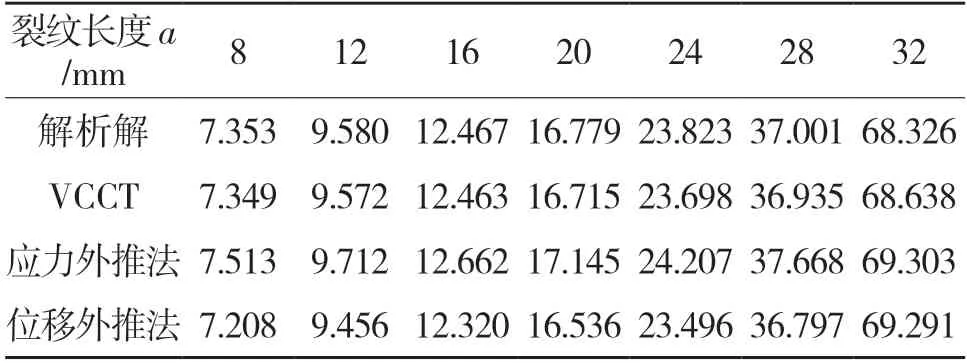
表3 不同裂纹长度时KI 的值Tab.3 KI values at different crack lengths

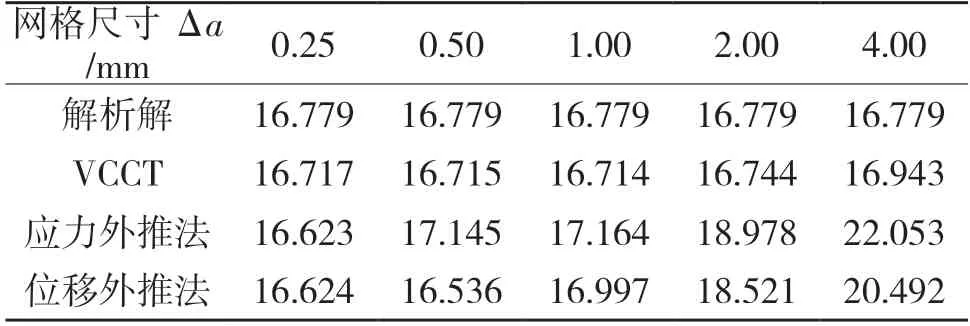
表4 不同网格长度时KI 的值Tab.4 KI values with different mesh lengths

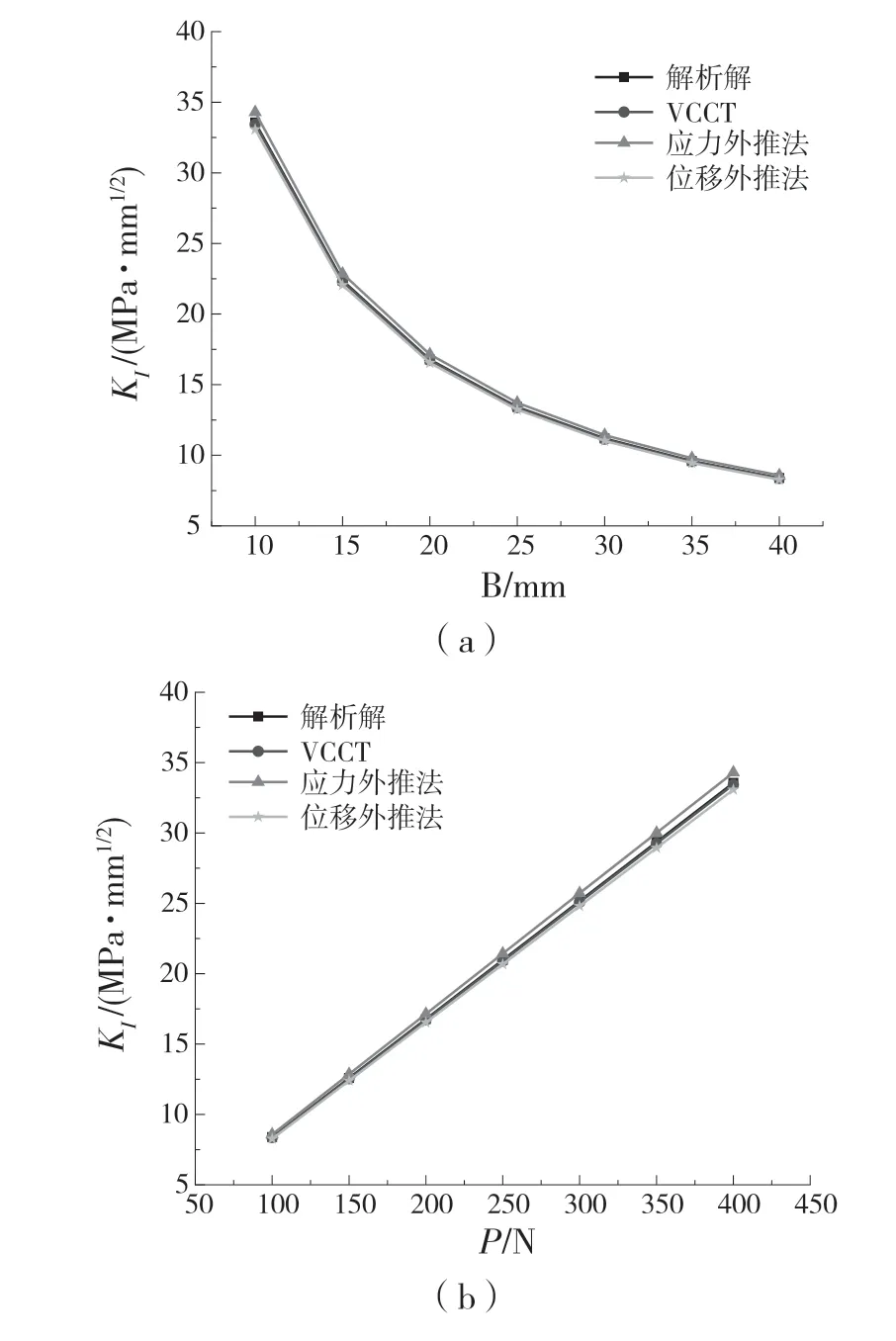
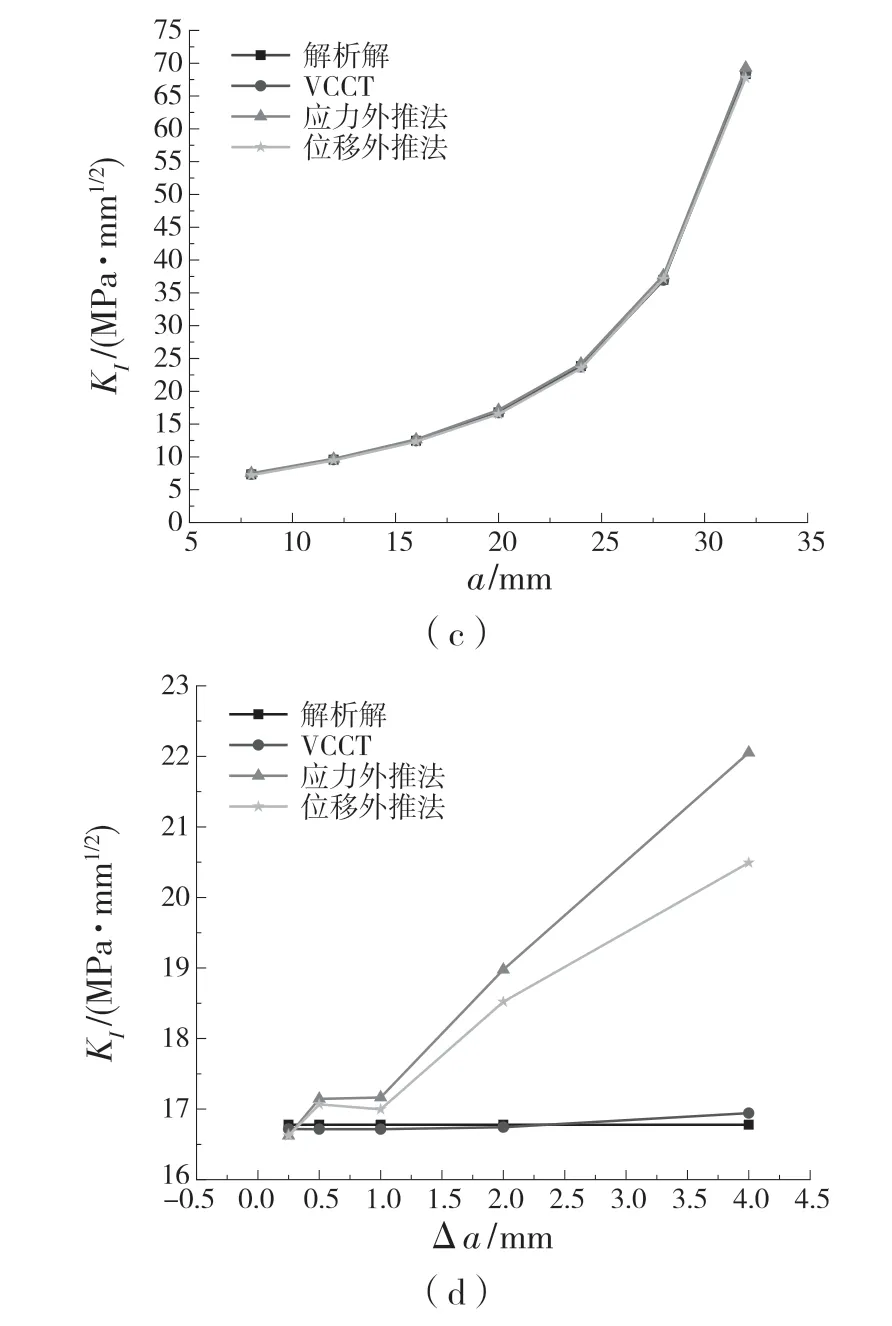
图3 不同条件下应力强度因子KI 的曲线比较Fig.3 Curve comparison of stress intensity factor KI under different conditions

比较网格尺寸对结果精度的影响，由表4 和图3（d）可知，当网格尺寸≤1 mm 时，3 种有限元法与解析解高度一致；当网格尺寸＞1 mm（Δa/a=0.05）时，随网格尺寸增大，应力外推法和位移外推法的误差越来越大，而VCCT 的结果仍然与解析解高度一致。

4 结论

（1）建立三点弯曲试样的有限元模型，使用虚拟裂纹闭合法、应力外推法、位移外推法来计算应力强度因子KI，并与解析解进行比较，误差都在2.5%以内，以上3 种方法在计算I 型裂纹应力强度因子方面具有可行性和较高的准确性。

（2）研究了试样的几何尺寸、裂纹长度及载荷大小对I 型裂纹应力强度因子KI的影响。KI与载荷P成良好的线性关系；KI随试样厚度B增加而减小，当W/B＜2 时，KI受B 影响较大；KI随裂纹长度a增加而增大，当a/W＞0.7 时，KI的增长速度明显增加。在分析网格尺寸对结果的影响中，2 种外推法的精度随网格尺寸增大而降低，虚拟裂纹闭合法始终保持1%以内的精度。

（3）分析比较了虚拟裂纹闭合法、应力外推法、位移外推法的特点，得到应力外推法的误差始终大于位移外推法，应力场需要通过位移场求偏导数，所以应力外推法精度比位移外推法低。而虚拟裂纹闭合法的精度均小于1%，且计算效率高。