某轿车空气悬架PID 控制系统仿真研究
2022-10-31刘斌徐晖
刘斌,徐晖
(200093 上海市 上海理工大学 机械工程学院)
0 引言
轿车的空气悬架系统由空气弹簧、减震器、导向机构和车身高度控制阀等部件构成,其工作原理是先由空气压缩机形成压缩空气,然后将清洁的空气送入气囊弹簧,再由电控单元根据轿车状况、驾驶员需求和轿车高度传感器传递的输出信号自动控制进排气门的开启与关闭,实现实时调节空气弹簧刚度和车身的垂向高度[1-3]。
被动悬架是传统的机械结构,在变化的工况下性能表现欠佳。空气悬架的优越性能表现在适应不同的使用工况,其控制策略尤为重要。PID 控制的优点是算法简单且易于实现,同时具备很好的消除系统稳态误差的优点,应用到空气悬架上能很好地改善轿车性能。马相飞[4]等人建立了膜式空气弹簧空气悬架PID 系统,分析了单工况下PID 控制对空气悬架参数的影响;刘维柳[5]通过对控制理论方法的研究,设计了PID 控制策略和模糊控制策略。
本文以某轿车空气悬架为对象,通过对主动空气悬架系统以及PID 控制特性的分析,在Simulink中搭建了二自由度空气悬架PID 控制系统模型,分析了在不同工况下空气悬架PID 控制系统性能。
1 空气悬架模型
空气悬架系统的构成相对复杂,可以根据实际情况具体分析,并对其进行简化和加以优化。本文选用的是二自由度1/4空气悬架模型[6],如图1所示。
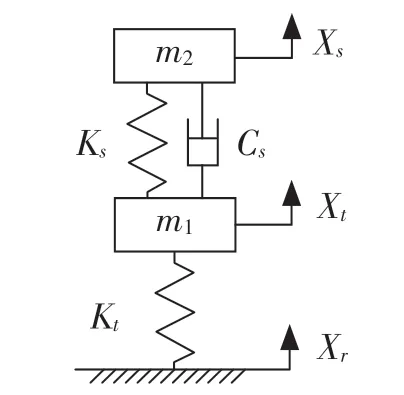
图1 二自由度1/4 空气悬架模型Fig.1 2-DOF 1/4 air suspension model
空气弹簧中产生的支撑力Fp可表示为:

式中:ks——空气弹簧的刚度;cs——悬架阻尼;xs——簧载质量位移;xt——非簧载质量位移。
由空气悬架模型和牛顿第二定律可得:
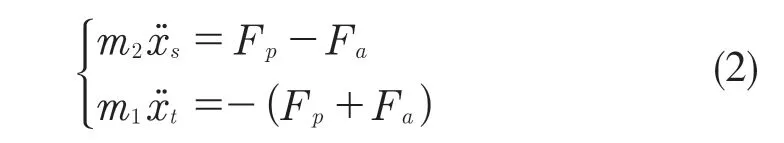
继而得到运动理想微分方程如式(3):

式中:m1——非簧载质量;m2——簧载质量;kt——轮胎径向刚度;xr——路面激励。
根据式(1)—式(3),建立如表1 所示的空气悬架的参数。

表1 1/4 空气悬架系统的参数表Tab.1 Parameters of 1/ 4 air suspension system
2 路面输入模型
为了进一步掌握路面平整度,需要创建路面粗糙度功率谱,并将轿车作为一个线性系统计算各物理响应率对应的功率谱,从而解释这些参数对应物理量对轿车平顺性评价的影响。假定路面相对基准平面的高度为xr,路面相对基准平面的高度为xr(L),又称路面粗糙不平度函数,可以通过水准仪或路面计这两种方法得到此函数。采用的道路粗糙度功率谱密度函数[7]表示为
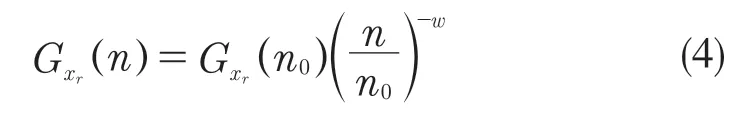
式中:n0——参考空间频率,n0=0.1m-1;——路面不平系数;w——频率指数。
国内主要的路面谱一般都在前4 级(A,B,C,D)范围内,路面不平系数分类表如表2 所示。
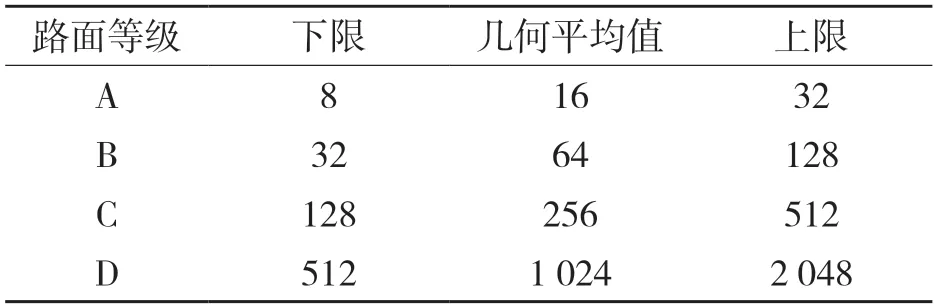
表2 路面不平度系数分类表Tab.2 Classification of road roughness coefficients
本文以滤波白噪声信号作为路面的输入,其时域表达式为
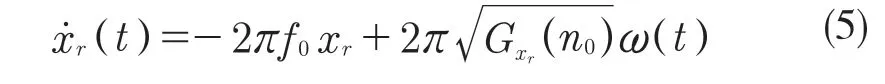
设置轿车车速为20 m/s,测试路面输入选B、C 级2 个占比相对较大的路面,w=2,B、C 级路面的不平度通过查表获得,在Simulink 仿真环境中白噪声函数随机产生的路谱由示波器显示。图2 所示为路面输入仿真模型。
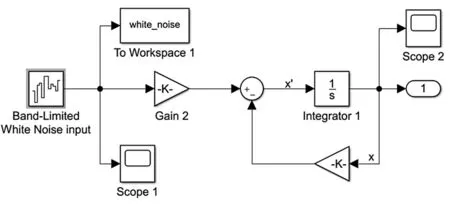
图2 路面输入仿真模型Fig.2 Pavement input simulation model
需要在Simulink 的仿真模拟环境中运行路面输入仿真模型,获取车速20 m/s 下B 级路面的不平度仿真域响应曲线与白噪声函数相关的路面粗糙不平度的时域响应曲线。如图3 所示为高斯白噪声输入时域响应曲线,如图4 所示为路面不平度仿真域响应曲线。
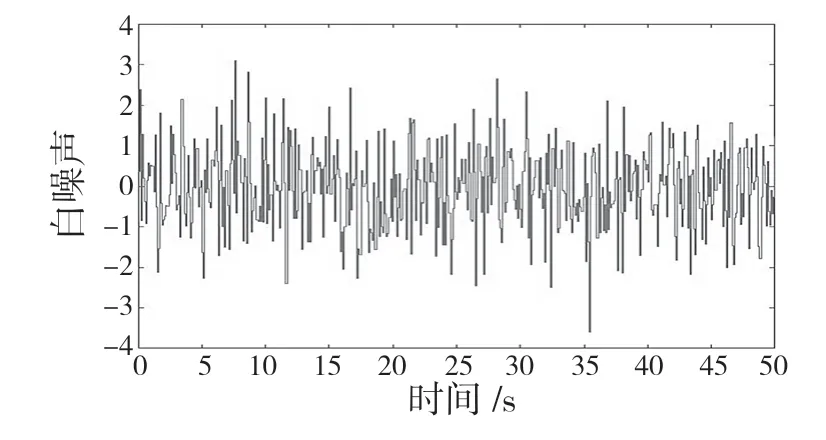
图3 高斯白噪声输入时域响应曲线Fig.3 Time-domain response curve of white Gaussian noise input
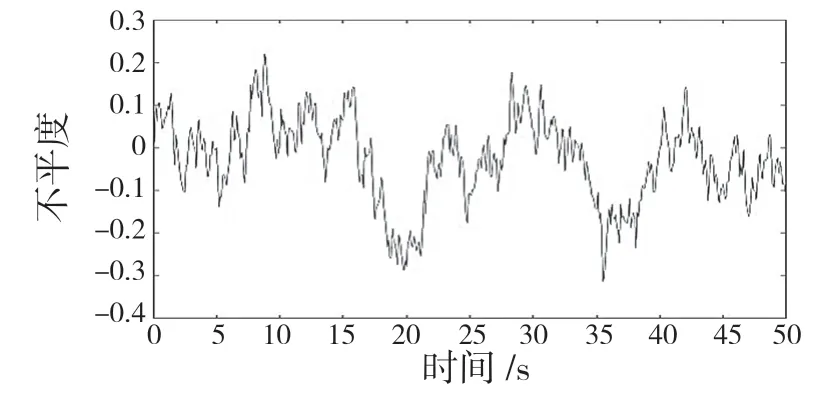
图4 路面不平度仿真域响应曲线Fig.4 Road roughness simulation domain response curve
3 PID 控制空气悬架模型
3.1 PID 控制基本原理
控制器的应用十分广泛,PID 控制器根据控制系统中比例、积分和微分环节的误差来处理不同参数的组合和控制,其控制算法一般为
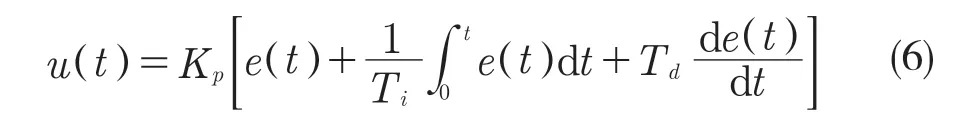
e(t)是由系统自定值r(t)和被测值c(t)形成的控制偏差信号,比例系数记作Kp,微分时间常数设定为Td,积分时间常数设定为Ti。基本原理框图如图5 所示。
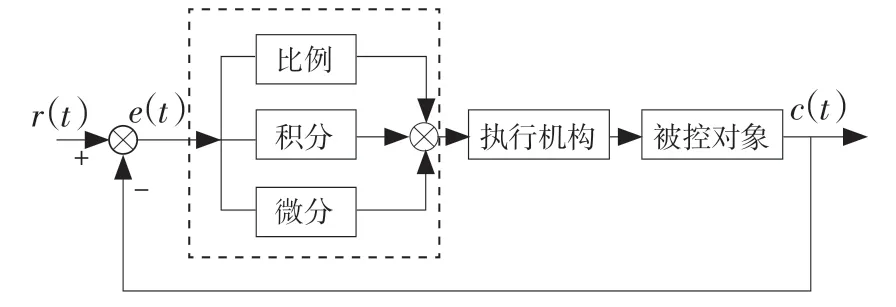
图5 PID 控制系统原理框图Fig.5 PID control system principle block diagram
为了更好地实现PID 控制,需要引入积分和微分项,此时PID 控制算法为
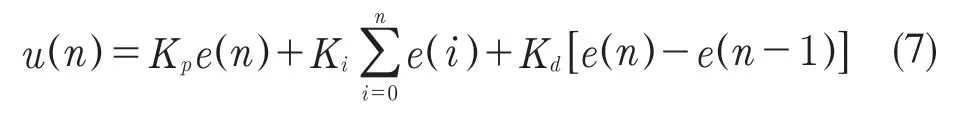
式中:Kp,Ki,Kd——比例常数、积分常数和微分常数。这3 个基本参数在实际运用中发挥着各自的作用。PID 控制器的技术水平取决于比例常数、积分常数和微分常数。
3.2 PID 控制器设计
PID 控制策略最重要的是3 个参数——Kp,Ki,Kd,这3 个参数间接反映系统的控制效果与能力。调整这3 个参数使得系统控制达到最佳,才能使空气悬架PID控制系统的轿车性能处于最佳。调节参数与系统时域性能指标之间有一定关系,如表3 所示。

表3 PID 调节参数与系统时域性能指标的关系Tab.3 Relationship between PID regulating parameters and system time-domain performance indexes
PID 控制器的控制效果首要是依据比例常数、积分常数和微分常数的这3 个参数来表达的。通过经验试凑法,按照比例、积分、微分顺序进行参数的设置及整定,经过多次仿真实验使PID 控制器达到最佳控制效果,最终得到Kp=1,Ki=53,Kd=0.1,并在Simulink 仿真系统中搭建PID 控制器仿真模型。
3.3 PID 系统的模型仿真
在Simulink 仿真系统中进行一些对于模块的操作、信号线连接和模块标注,以设计出道路激励模型仿真图,从而可以应用连续模块库中相对应的积分模块、数学模块中的增益、乘法以及求和,再凭借输出模块中的示波器模块等设计所需要的被动空气悬架的Simulink 仿真模型,如图6 所示。
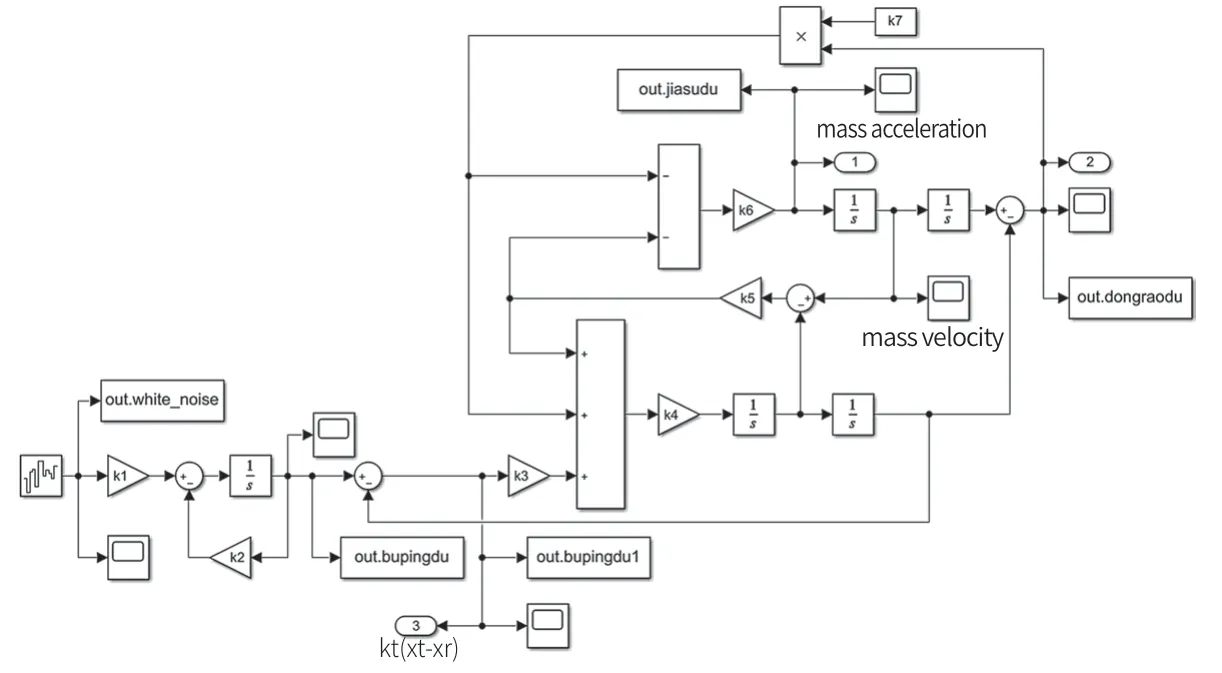
图6 PID 控制器仿真模型Fig.6 PID controller simulation model
运用模块先建立好PID 控制系统的仿真模型,然后借助Simulink 的示波器模块显示所对应的输出波形并观察,同时可以在MATLAB 中通过Piot 绘图函数观察及比较相应系统的时域响应曲线。本文研究和模拟了轿车在2 种主要的行驶工况下空气悬架的性能变化,第1 种工况:车速为54 km/h 时在B 级路面上的行驶工况;第2 种工况:车速为40 km/h 时在C 级路面上的行驶工况。经由过程确立一些与之相对应的参数完成系统体系模型的建立,并通过仿真模拟环境输出进一步观察。如图7 是设计的所需完成的基于PID 控制悬架仿真模型图。
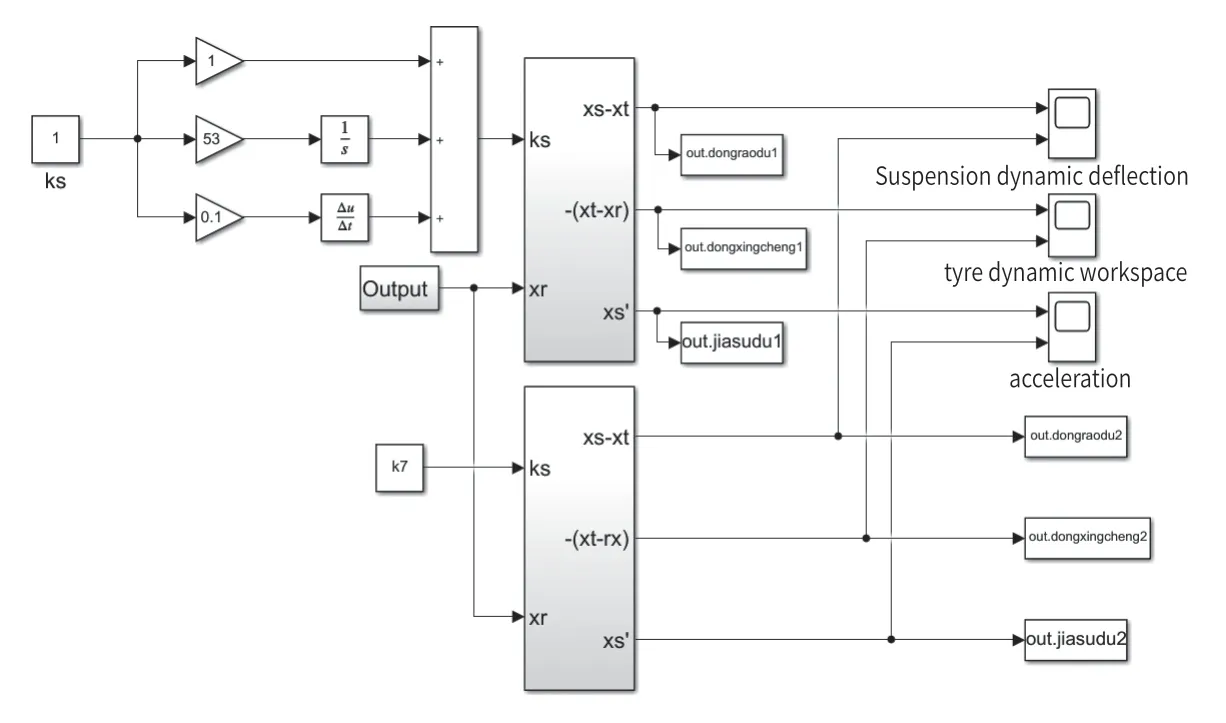
图7 被动悬架仿真模型Fig.7 Passive suspension simulation model
4 空气悬架系统的动力仿真结果及分析
4.1 PID 控制空气悬架仿真结果
利用建立的轿车空气悬架PID 控制系统模型和普通控制空气悬架(被动空气悬架)模型,在2种行驶工况(40 km/h 时C 级路和54 km/h 时B 级路面)下进行仿真,得到悬架动挠度的时域响应曲线、轮胎动态行程的时域响应曲线和车身垂向振动加速度时域响应曲线,分别如图8—图13 所示。
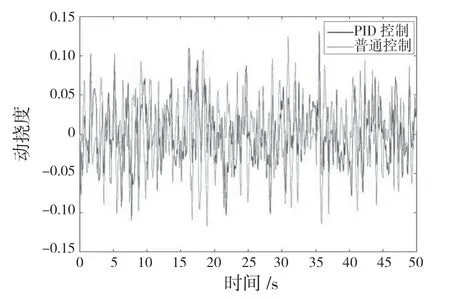
图8 40 km/h 时C 级路面悬架动挠度Fig.8 Dynamic deflection of C-grade pavement suspension at 40 km/h

图9 54 km/h 时B 级路面悬架动挠度Fig.9 Dynamic deflection of B-grade pavement suspension at 54km/h
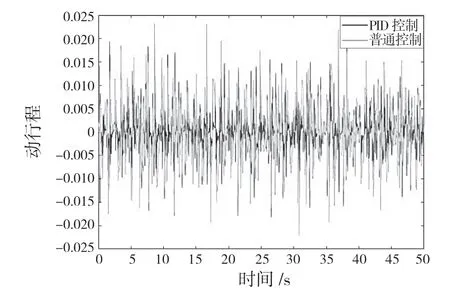
图10 40 km/h 时C 级路面轮胎动行程Fig.10 Dynamic travel of C-grade road tire at 40 km/h

图11 54km/h 时B 级路面轮胎动行程Fig.11 Dynamic travel of B-grade road tire at 54 km/h
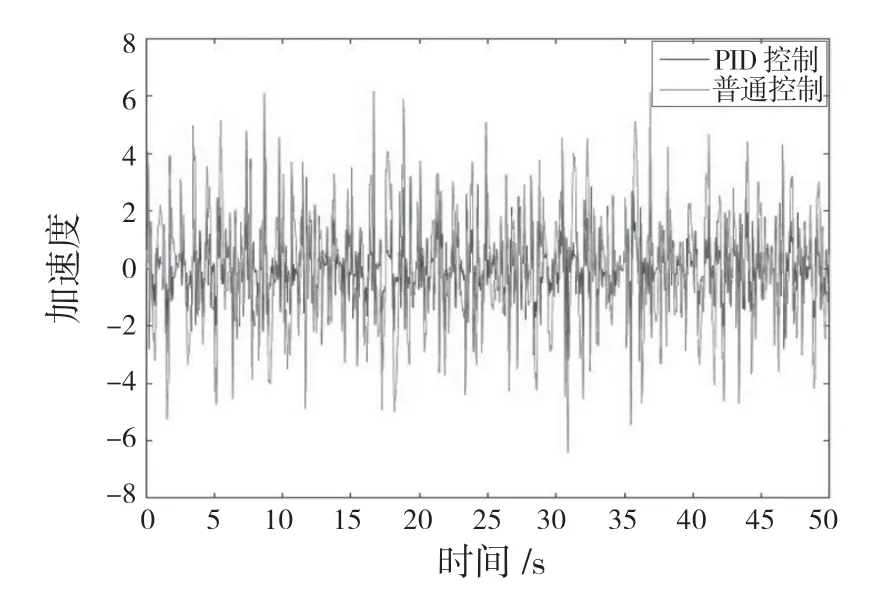
图12 40 km/h 时C 级路面车身垂直方向振动加速度Fig.12 Vertical vibration acceleration of C-grade pavement body at 40 km/h

图13 54 km/h 时B 级路面车身垂直方向振动加速度Fig.13 Vertical vibration acceleration of B-grade pavement body at 54 km/h
由图8—图13 可以看出,轿车空气悬架PID控制系统和被动空气悬架系统的悬架动挠度、路面轮胎动行程和车身垂向振动加速度的波动范围差别很大。在2 种工况下,空气悬架PID 控制系统相较于被动空气悬架系统,其悬架系统的悬架动挠度、路面轮胎动行程和车身垂直方向振动加速度的波动范围都较小。
4.2 仿真分析
由仿真得到的2 种行驶工况下的PID 控制空气悬架系统和被动空气悬架系统的车身垂直方向加速度、轮胎动行程以及悬架动挠度的信号值,再由Simulink 进行均方根统计仿真,得到2 种工况下这3个性能指标的加权均方根值,分别如表4、表5 所示。
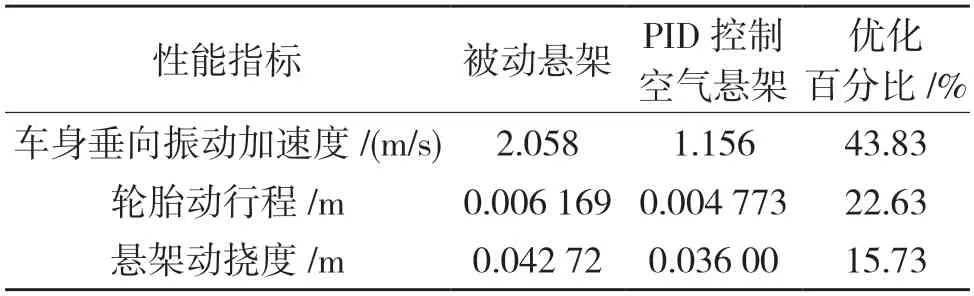
表4 40 km/h 时C 级路面加权均方根值性能对比Tab.4 Performance comparison of weighted root value of C-grade pavement at 40 km/h
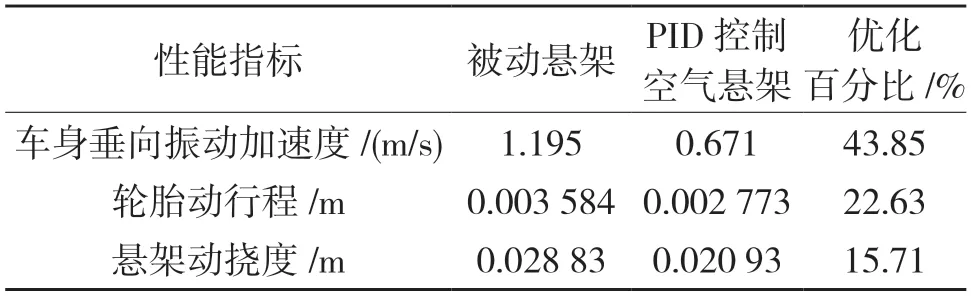
表5 54 km/h 时B 级路面加权均方根值性能对比Tab.5 Performance comparison of weighted root value of C-grade pavement at 54 km/h
结合3 个性能指标的时域响应曲线和表4、表5 给出的均方根值以及优化百分比可知,轿车空气悬架PID 控制系统与被动空气悬架相比,空气悬架PID 控制系统的3 个主要性能更趋于稳定,其中对车身垂向振动加速度的优化最大接近44%,对悬架动挠度的优化最小接近23%,且2 种行驶工况下PID 控制空气悬架优化程度相差不大并趋于稳定;从优化百分比可见,PID 控制空气悬架仍有一定的性能提升潜力。
PID 控制策略应用到空气悬架系统上,带来的控制效果进一步降低了振动,达到轿车需要的性能要求。空气悬架PID 控制系统更大程度地满足乘坐舒适性和操纵稳定性及安全性等方面的需求。
5 结论
本文以轿车空气悬架为主要研究对象,利用MATLAB/Simulink 分别建立了被动空气悬架系统和PID 控制空气悬架模型,对2 种不同的悬架系统分别在2 种工况下进行仿真分析。结果表明,应用PID 控制空气悬架系统的3 个性能指标都有很大程度的优化,空气悬架的性能得到了很大提升,更好地满足操纵稳定性和乘坐舒适性的需求。同时,仿真分析结果可为进一步优化PID 控制空气悬架性能提供参考。
