探究分数乘除法解决问题的策略

江西财经大学附属中学小学部 顾金华

《义务教育课程方案（2022年版）》要求各门课程基于培养目标，将党的教育方针具体化为学生核心素养发展要求，明确本课程应着力培养的正确价值观、必备品格和关键能力。探究分数乘除法解决问题的策略，培养学生学习数学的品格和关键能力是当前所需、当务之急。

一、探究背景

（一）内容重要，分布广泛

“分数”内容主要分布在人教版数学三年级上册、五年级下册、六年级上册等教材中。

（二）内容复杂，思维抽象

用乘除法解决分数问题，堵点多、难度大，稍复杂的分数问题比较抽象。如对于确定中间问题比较量对应的分率计算方法，学生知识迁移不够顺畅。

（三）打好基础，利于学段纵向衔接

分数乘除法解决问题在后续的学习中应用比较频繁、广泛。比如，实际问题与解方程、销售中的盈亏等很多内容涉及分数问题。因此，学懂、弄通分数问题能为后续的学习打下扎实的基础。

（四）应用广泛，“一起向未来”

生活中的增长问题、节约问题、折扣问题、递增问题、利率问题、税率问题，营销中的盈亏问题，统计中的百分率等都是分数乘除法解决问题的应用。在生活中，分数问题更是无处不在。掌握好用分数乘除法解决问题的策略，我们才能更好地“一起向未来”。

二、探究策略

（一）“准”：定准单位“1”

1.理解单位“1”，感知单位“1”

皮亚杰认知发展阶段论认为，人的认识来源于动作，动作是感知的源泉和思维的基础。

学习“分数的意义和性质”时，学生能根据直观图写出分数，表述把什么看作单位“1”，分数表示什么的几分之几。分数的意义中的难点是把一些物体看作单位“1”。

2.两种数量比较时，定准单位“1”

两种数量比较时，教师要助力学生改变认知结构，完成认识顺应，达到新的认知平衡。

第一，一个数的几分之几，把一个数看作单位“1”。第二，与什么比，就把什么看作单位“1”。把分数问题和倍数问题进行统一，与什么比，什么就是标准，即单位“1”的量。

3.复杂多变时，定准不变的量为单位“1”，或统一单位“1”的量

（二）“稳”:数形结合，分析透彻，稳妥解题

1.简单分数乘法问题

数形结合，理解并掌握求一个数的几分之几用乘法计算，归纳整理数量关系式。比如，人教版数学六年级上册“分数乘法”第5页第4题，首先，教师让学生初步掌握“求一个数的几分之几是多少”用乘法计算，养成自主画图的习惯。（如图1）

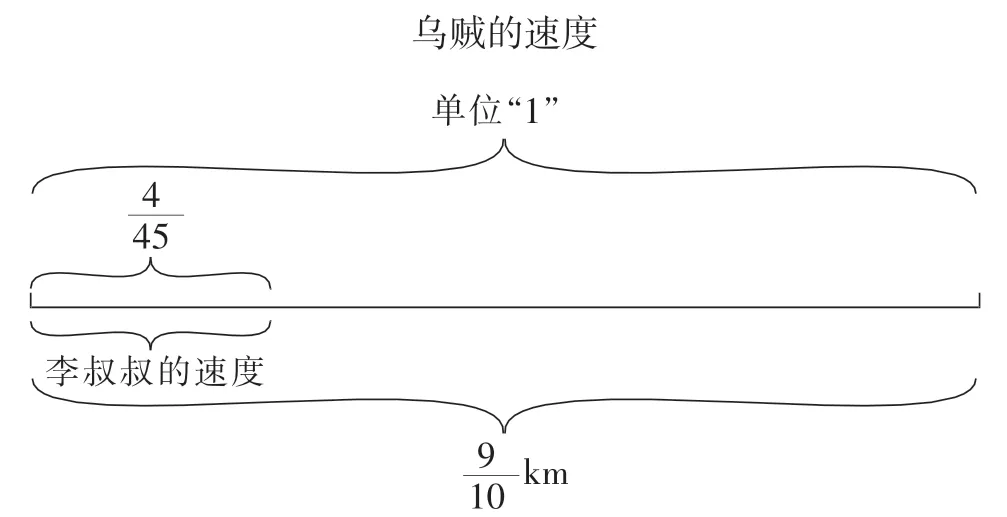
图1

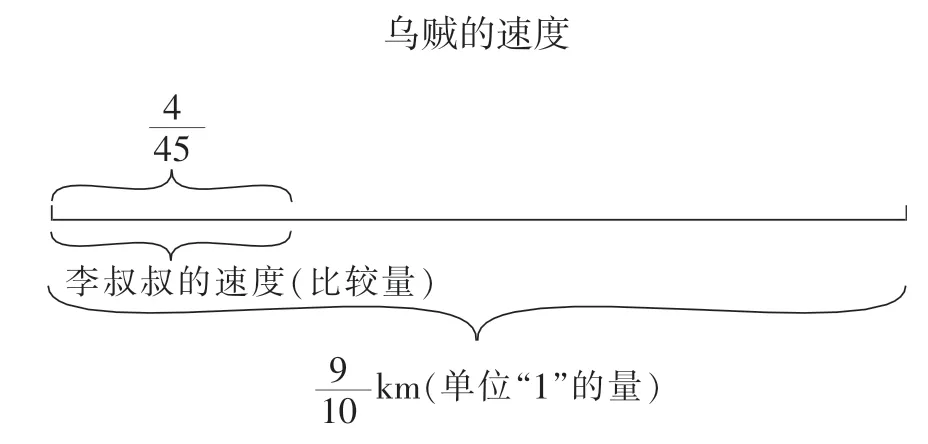
图2

2.简单分数除法问题

逆向思维理解困难时，学生可依托线段图，借助顺向思路，熟练掌握问题“已知一个数的几分之几是多少，求这个数”的解题方法，用方程和除法解答，归纳数量关系。例如，人教版数学六年级上册“分数除法”第35页例4，首先，我们根据关键条件“水分占体重的4—5”，体重是单位“1”的量，水分28kg是比较量，水分对应的分率是

4—5，准确地画出线段图，标出条件与问题（如图3）。根据图3，我们可将题目提炼成文字题：已知一个数的是28，求这个数。在条件与问题之间建立顺向的等式关系：小明的体重×明的水分28kg，列出方程并解答。再根据顺向数量关系，推出用除法解决问题，得出解决问题的逆向数量关系式。求小明的体重用除法计算在图中标出三个数量：单位“1”的量、比较量、对应的分率（如图4）。最后归纳整理：比较量÷对应的分率=单位“1”的量。如此，为学习用较复杂的分数除法解决问题做铺垫。

图3

图4

（三）“精”：精准捕捉稍复杂的分数问题的核心

抓住复杂问题的核心，突破难点、突出重点，为解决复杂问题保驾护航。比如，人教版数学六年级上册“分数乘法”第13页例9和人教版数学六年级上册“分数除法”第36页例5，都是稍复杂的分数问题。核心问题1：找准单位“1”的量，再确定比较量及比较量对应的分率。如图5，隐去其他具体的数量，显示单位“1”和另外一个已知分率，便于学生理解求比较量对应分率的计算方法。核心问题2：最后问题求什么量，选择合适的解答方法。结合线段图（如图6）。无论多复杂的问题，抽丝剥茧后，都会转变成简单的问题。例9：表示求75的是多少，求比较量，用乘法计算。例5：已知一个数的是35，求这个数，求单位“1”的量，可以用算术法解答，也可以用方程解。

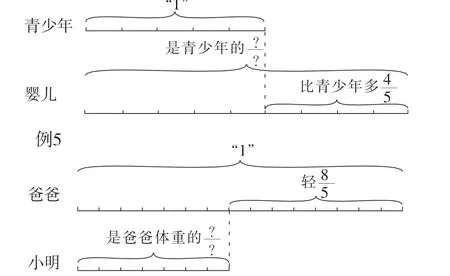
图5

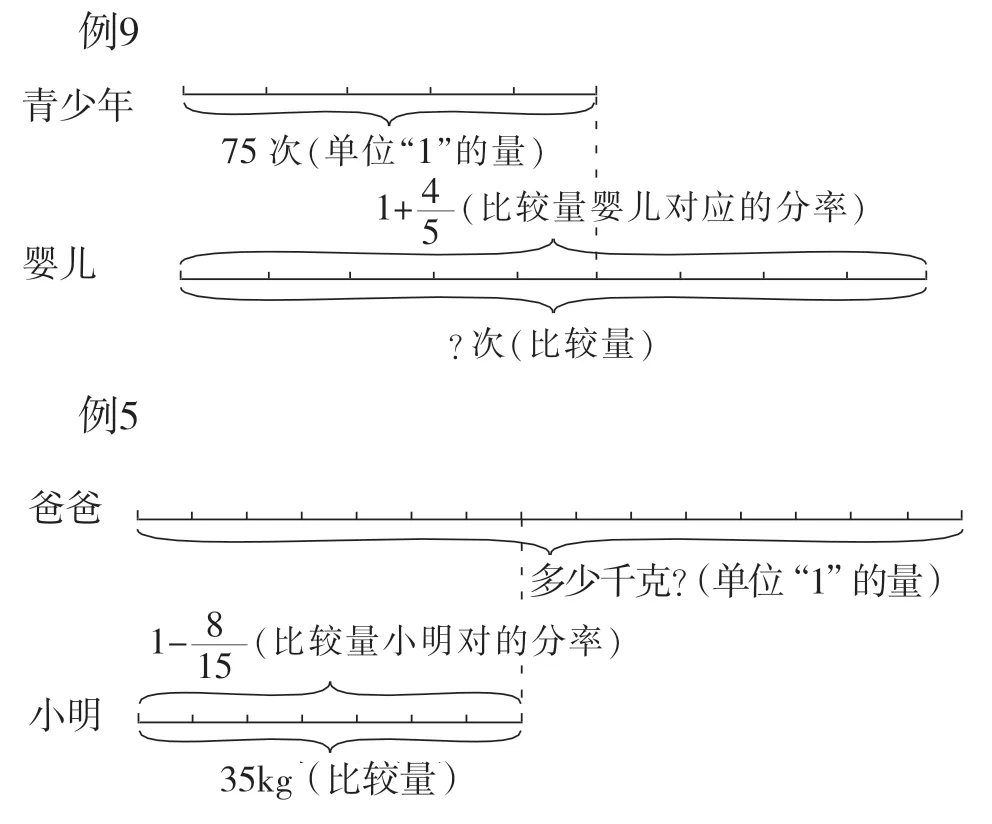
图6

例9

（四）“通”：注重学科内知识关联，融会贯通

世间万物都不是孤立存在的，它们之间存在千丝万缕的联系。知识点之间同样如此，分数、百分数、比、比例之间存在着密切的联系。学生要具有融会贯通的能力，能从不同的角度来解决分数乘除问题，达到学活、用活的高阶思维能力。

1.用比例知识解决分数乘除问题

抓住条件和问题，罗列两组数据。如“分数乘法”第5页的例4：

2.将复杂问题的条件进行转化，培养高阶思维

转化思想是数学的一种重要思维方法。对于综合性、挑战性强的分数问题，灵活地运用所学关联知识，融会贯通，有效转化，可以培养学生的高阶思维。

第一种：将比转化成分数。例如，快递公司配送一批加急件，已配送的件数与剩下的件数之比是3：4，如果再配送72件，正好配送这批加急件的这批加急件一共有多少件？我们可以把条件“已配送的件数与剩下的件数之比是3：4”，转化成“已配送加急件是这批加急件的与条件“再配送72件，正好配送这批加急件的的单位“1”统一起来，从而突破问题难点。

第二种：将分数转化成比。例如，某校开展了兴趣班，围棋小组和魔方小组一共有40人，魔方小组人数是围棋小组的围棋小组和魔方小组各有多少人？这道题除了可以用和倍问题解答方法进行解答，还可以把条件“魔方小组人数是围棋小组的转化成“魔方小组人数与围棋小组人数之比是3：5”，就成了典型的按比分配问题，如此，将难点化整为零，通俗易懂。

第三种：复杂信息化繁为简。例如，张阿姨买了三筐同样重的橘子，取出第一筐质量的第二筐质量的，从第三筐中取出12kg，这时，三筐中剩下的橘子恰好等于原来两筐橘子的质量。原来每筐橘子有多重？面对这个看似复杂的题目，我们要抓住烦冗的信息，将条件“张阿姨买了三筐同样重的橘子”“这时剩下的橘子恰好等于原来两筐橘子的质量”转化成关键条件“一共取了一筐橘子”，再找到比较量“12kg”对应的分率，问题便迎刃而解。如此，化繁为简，有助于学生分析问题。

（五）“深”：编题说题，深度学习，培养能力

美国学者爱德加·戴尔提出的“学习金字塔”中，主动学习有三项：教授给他人、实践、讨论。学习内容平均留存率：讨论50%、实践75%、教授给他人90%。因此，编题、说题是自主学习的高级阶段，也是提质培优的有效手段之一。学生具有一定的解决分数问题的能力后，在教师的引导下，根据不同类型分数问题的算式创编生活中各种情境问题。同学之间互换互评、互练互讲，进入学习的输出阶段，使所学知识得到升华，达到深度学习的效果。

三、策略回馈，青草更青，春意盎然

经过有目的、有计划、有梯度的探讨和学习，教学效果初现端倪，探究策略在教学中得到有效体现。六年级两个班112名学生参加测试，其分数乘除法解决问题的正确率为89.17%，逆向较复杂的分数解决问题的正确率为82.31%。对于其中一道问题，学生的解答正确率达91.07%，其解答有多种解法：归一法、将两数之差看作单位“1”、用比例解答、用倍比法解答等。

在用乘除法解决分数问题的教学中，教师要抓住学习的有效落点，分散难点、突出重点、化难为易、化繁为简，形成学习的捷径；培养学生的分析能力、判断能力、迁移能力、逻辑思维能力；让学生能解、能说、能评、能编，达到自主学习的高级阶段，有效培养高阶思维，达到深度学习的效果。