增强型电磁轨道炮导轨的多场耦合分析与研究

王烝，赵南南，苏子舟，王栋，白天羽

(1.西安建筑科技大学 机电工程学院，陕西 西安 710055；2.西北机电工程研究所，陕西 咸阳 712099)

电磁轨道炮具有发射速度快、可操控性能好等优点，在军事、民用等领域有巨大的应用潜力。轨道炮主要由脉冲电源、导轨和电枢构成，在强磁场的作用下电枢受到电磁推力，可急剧加速后以高速发射出膛口。电磁轨道炮在发射时，导轨和电枢会产生烧蚀、变形等现象，关系到轨道炮的效率、寿命、精度等性能，因此为了研究轨道炮在不同物理场下的变化规律，需要建立相关的理论来指导工程实践。

许多国内外学者针对电磁轨道炮的不同物理场特性进行了相关研究。文献[1]提出了一个包含接触电阻和摩擦因素的滑动电接触模型，研究了模型的效果；文献[2]获得了轨道的瞬态温升分布特性，并进行了相应的热管理；文献[3]给出了枢轨的瞬态焦尔热及其温升的计算方法；文献[4]分析了轨道炮枢轨接触面间的接触电阻特性；文献[5]对电磁轨道炮接触电阻的热时空分布特性进行了仿真计算，但没有分析接触电阻热和摩擦热共同作用下对轨道炮瞬态温升时空分布特性的影响；文献[6]建立了三维瞬态温度场模型，研究了轨道炮的温度分布特性，但没有考虑接触电阻热以及摩擦热的瞬态特性；文献[7]研究了增强型电磁轨道炮主轨道的瞬态温升时空分布，考虑了接触电阻的瞬态变化，但没有与结构场进行耦合分析；文献[8]研究了轨道炮导轨的受力与变形问题，但忽略了热效应对导轨扩张量的影响。

在上述研究中，研究者尚未对增强型电磁轨道炮的主轨和外轨同时进行三维瞬态多场耦合分析，研究电磁发射过程中双轨的电磁加载、高温烧蚀、结构形变等问题。因此，针对上述问题，笔者从接触电阻热量瞬态特性、摩擦热量瞬态特性的角度，建立增强型电磁轨道炮在脉冲电流下的电磁-温度-结构耦合物理模型，计算在接触电阻热源项与摩擦热源项共同作用下双轨的瞬态温升分布以及瞬态扩张量分布。

1 增强型电磁轨道炮原理

平面式增强型电磁轨道炮主要由脉冲电源、主轨道、外轨道和电枢组成，脉冲电流从主轨道流入，经过电枢、主轨道和外轨道，最后从外轨道流出。与普通轨道炮相比，增强型电磁轨道炮在没有提高电流的基础上使主轨道与外轨道在膛内形成的磁场相互叠加，电枢由此受到了更强的洛伦兹力，以更高的运动速度出膛，提高了电枢的出膛速度与电能利用率，其基本原理示意图，如图1所示。

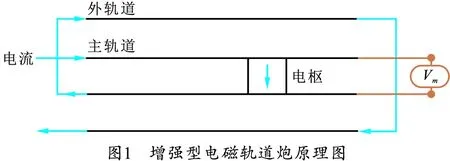
2 计算模型与参数

通过文献[9]脉冲电流波形研究发现，采用梯形波的效果最佳。笔者采用的电流波形如图2所示，其中，脉宽为1.5 ms，峰值为500 kA。

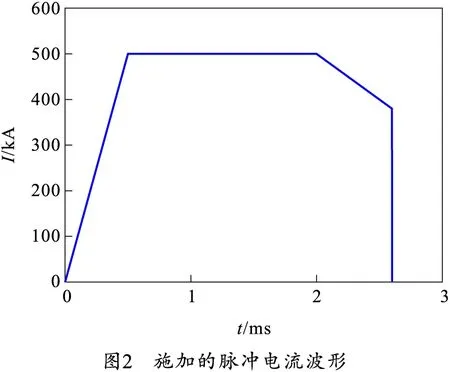
电枢与轨道的求解模型如图3所示。通过文献[7]研究发现，凸轨结构可以更好地避免导轨表面出现电流密度高度集中而引起的局部高温现象，因此本文主轨道采用凸轨形式。模型中主轨道的长度为3 m，宽度为50 mm，厚度为15 mm，为凸轨形式；外轨道的长度为3 m，宽度为50 mm，厚度为10 mm，为平轨形式。主轨道与外轨道之间有一层3 mm厚绝缘板。轨道材料采用铜合金，电枢材料采用铝合金。

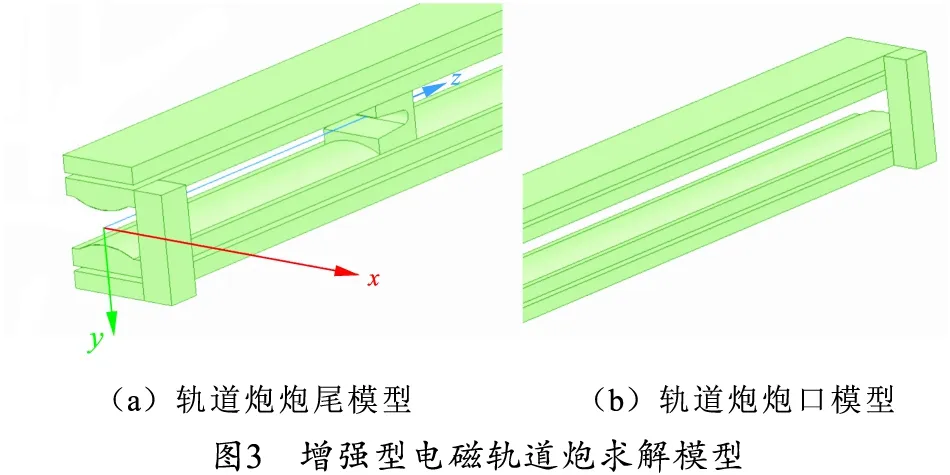
3 热源计算与分析

电枢高速运动时，电磁发射装置会产生大量的热，枢轨接触面间的热量主要来源于脉冲电流产生的焦耳热、电枢运动过程中产生的接触电阻热和摩擦热。其中，焦耳热是由脉冲电流在流经轨道和电枢时产生的，主要分布于枢轨导体内部；接触电阻热是由接触电阻产生的，主要分布于枢轨接触面表面；摩擦热是由电枢在轨道上滑动摩擦过程中产生的，主要分布于接触面表面。本节对电磁轨道炮的不同热源进行了计算分析。

3.1 计算条件

在计算过程中，由于目前有限元软件不能直接模拟电磁发射全过程，为了使电枢运动过程更加精确化，笔者把轨道分为10段进行模拟计算，分别为X0，X1，…，X9。其中，X0为电枢起始位置到炮尾的距离即200 mm，X1为脉冲电流上升期间的电枢位移即38 mm。根据文献[6,8]可知，在电枢发射初始阶段，轨道温升和形变较大，因此为了使模拟结果更为准确，在此阶段对轨道进行细分，每段为150 mm左右，即设定X2～X5分别为141.2，150.8，151.1，153.0 mm；在电枢之后的运动过程中，为简化计算对轨道分段为500 mm左右，即设定X6～X9分别为535.4，488.2，544.6，597.7 mm。在电枢高速运动过程中，越接近炮口处，施加的电流波形相比于起始位置就越短且滞后，因此对10段轨道施加不同的电流波形，方法示意图如图4所示。

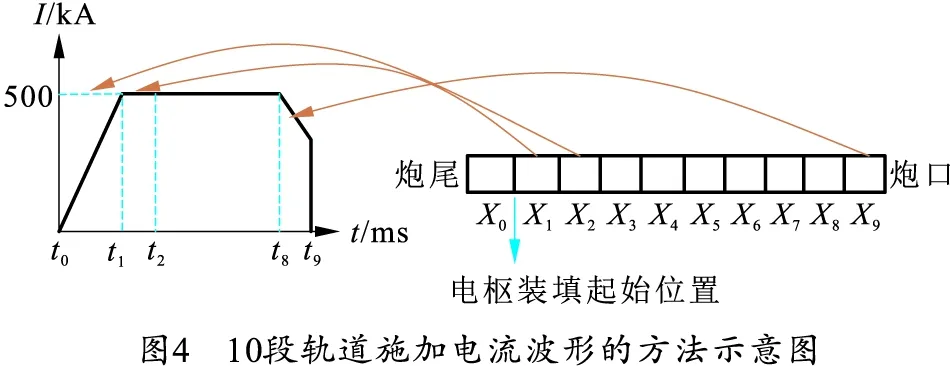
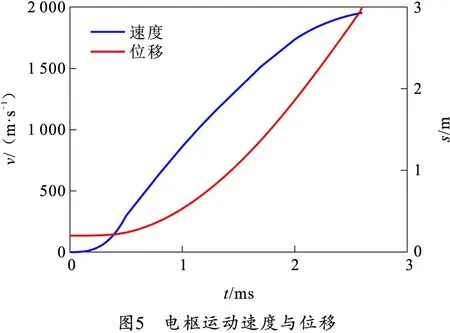
假设在步进时间0.02 ms内电枢受到的推力均匀，利用式(1)与式(2)可以得到电枢的运动速度和位移[10]，如图5所示。

(1)

(2)

式中：∑F=Fx-Ff=Fx-cFy；c为摩擦因数，在高速滑动中，铜铝之间的摩擦系数接近于0.2[11]，故c取0.2；m为电枢质量，取80 g。

3.2 电流焦耳热计算

在电磁炮发射过程中，脉冲电流流经轨道和电枢由此产生电流焦耳热。在时间段[t1,t2]内，枢轨内部焦耳热的计算公式为

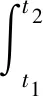
(3)

式中：i(t)为脉冲电流值；R(t)为轨道或电枢的电阻值。在温度场计算中，电流焦耳热可从电磁场直接耦合加载。

3.3 接触电阻热计算与分析

在两个金属的接触过程中，粗糙的接触面将刺破金属表面氧化层和污染膜层，微小的接触斑点由此形成。在电枢运动过程中，脉冲电流将流经这些接触斑点，产生接触电阻[12-13]。接触电阻可以体现发射过程中枢轨接触状态的变化趋势，研究接触电阻在电枢运动过程中的瞬态特性，有利于提高轨道炮的精度与寿命。电枢运动过程中接触电阻产生的热量主要分布在电枢和主轨的接触面上，其中接触电阻可由式(4)计算所得，在时间段[t1,t2]内接触电阻产生的热量由式(5)计算所得。

(4)

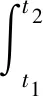
(5)

式中:Um(t)为炮口电压；Rc(t)为接触电阻；M(t)为主轨炮口段与外轨互感。

式(4)构建了枢轨接触电阻与炮口电压、脉冲电流和轨道互感的关系，增强型电磁轨道炮炮口电压的测量如图1所示[7,14]。通过有限元仿真计算可以得到轨道互感随电枢位移变化M(s)。根据M(s)和图5所示的电枢运动位移变化曲线，可以得到M(t)；根据测得的炮口电压、脉冲电流和轨道互感可以得到接触电阻Rc(t)。

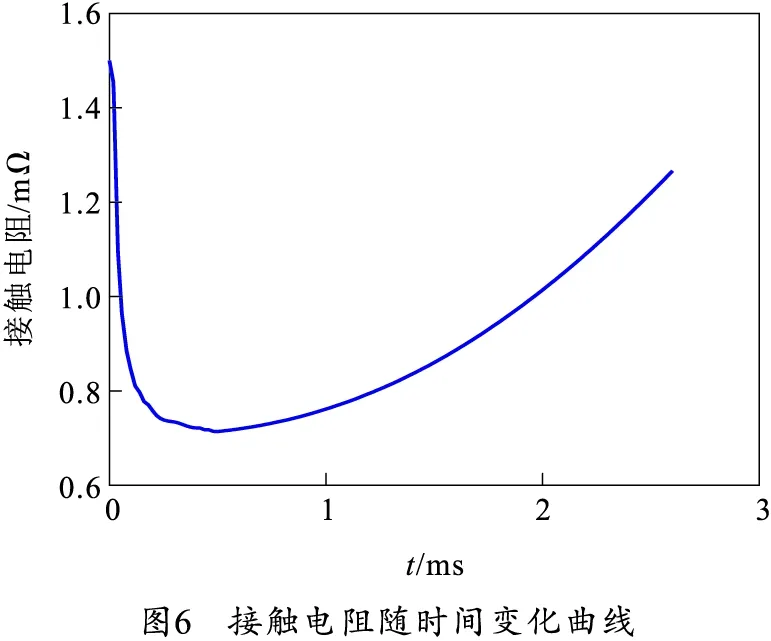
发射过程中接触电阻变化曲线如图6所示。由图6可知，在发射初期，接触电阻最大约为1.5 mΩ，在整个发射期间接触电阻不断变化，随着时间的变化先急剧减小，然后平稳增加。

轨道单位长度传导的接触电阻热随电枢位移变化曲线如图7所示。可以看出，在炮尾位置，枢轨间的接触电阻热量最大，随着电枢的高速运动，接触电阻热量迅速下降。通过分析变化曲线可知，在发射初期，虽然接触电阻在不断减小，但是脉冲电流在急剧增大，从而使单位长度轨道传导的接触电阻热量迅速增加。在发射后期，脉冲电流缓慢减小，接触电阻热量也在平稳下降。

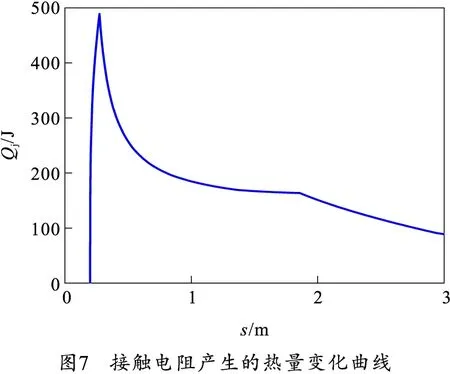
3.4 枢轨滑动摩擦热计算与分析

滑动摩擦是导致枢轨接触面间产生热量的另一个重要因素。在时间段[t1,t2]内摩擦热量计算公式为

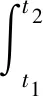
(6)

式中：μ为摩擦系数；N为枢轨接触压力。

枢轨接触压力对电枢出膛速度以及能量转换效率有着重要影响。枢轨接触压力过大会使电枢运动过程中受到较大的摩擦阻力从而降低出膛速度，枢轨接触压力过小会导致枢轨接触状态不佳，影响脉冲电流通过[15]。

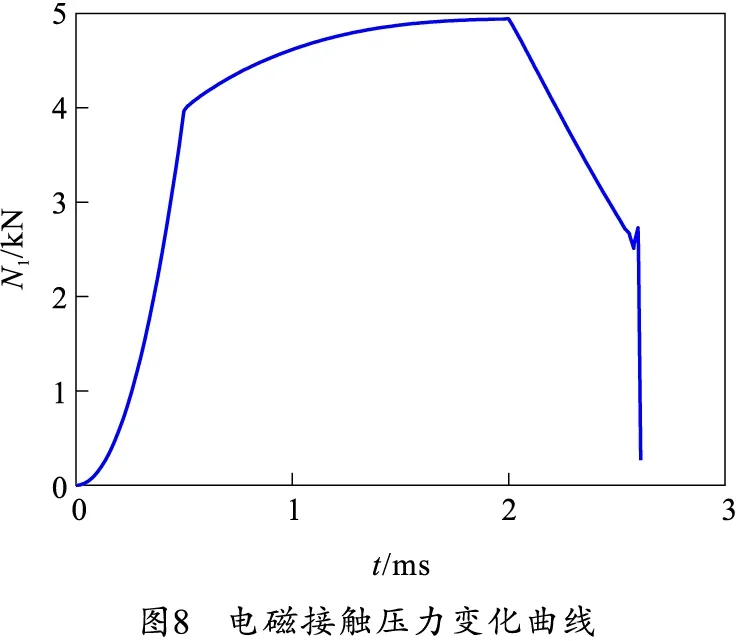
枢轨接触压力N由电磁接触压力N1和预紧力N2两部分组成。其中，电磁接触压力N1是由电磁场仿真求得电枢运动过程中不同时刻接触压力的瞬态值，如图8所示。增强型电磁轨道炮的炮身结构由导轨、电枢、外壳以及绝缘支撑件组成。为简化计算，将外壳对轨道的紧固作用化作弹性支撑。预紧力N2基于“安克法则”取定值进行计算[16]。

经计算得到了单位长度传导的摩擦热量随电枢位移变化曲线，如图9所示。

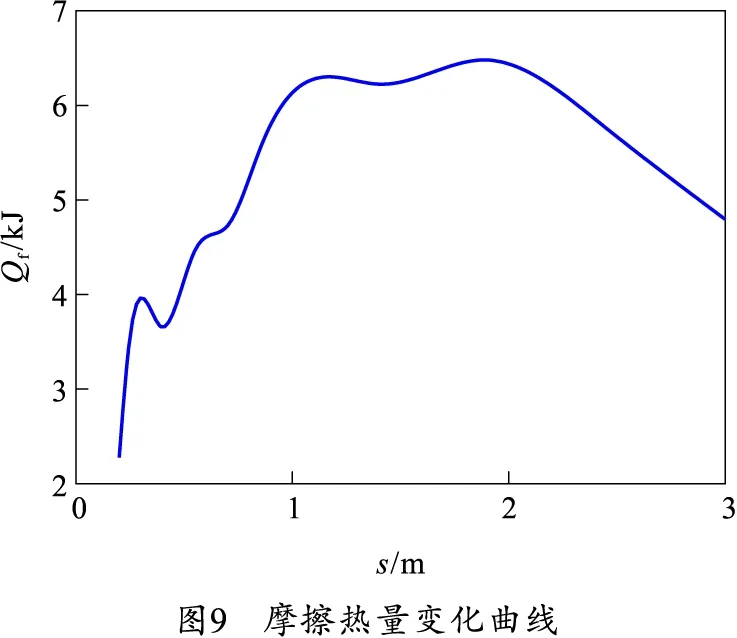
从图8中可以看出，电磁接触压力呈现出先增加然后平稳过渡最后下降的趋势，与脉冲电流变化曲线呈正相关。从图9可以看出，随着电枢的高速运动，枢轨间产生的摩擦热量也在不断变化。在电枢运动到轨道中部位置1～2 m时，单位长度传导的摩擦热量达到最大值6.5 kJ。

综上所述可知，在电枢运动初始阶段，枢轨接触面间产生大量接触热，随后接触热降低，最后趋于稳定；摩擦热量随着电枢的高速运动先不断增加然后减小。与接触电阻热量相比，摩擦热量占比较大。

4 多场耦合仿真与分析

4.1 瞬态电磁场仿真计算

4.1.1 电磁场数学模型

通过引入矢量磁位和标量电位，用磁扩散方程和电流连续性方程可以求解电磁场问题，满足

(7)

(8)

式中：A为矢量磁位；φ为标量电位；σ为电导率；μ为磁导率。

4.1.2 电磁场计算结果

根据上述计算模型及相关参数，利用ANSYS软件对增强型电磁轨道炮进行了瞬态电磁场的仿真计算。图10、11分别为磁场峰值时刻轨道炮电流密度与磁感应强度分布云图。

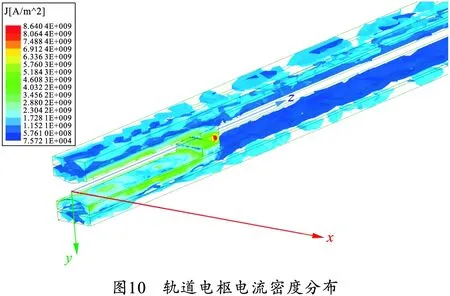
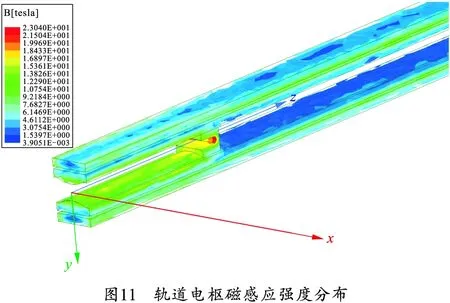
从图10、11中可以看出，在电场中，电流密度受到趋肤效应的影响主要分布于导轨内表面与电枢开口位置，最大值为8.6 GA/m2，容易由此造成放电烧蚀现象；在磁场中，电枢到炮口位置之间的主轨道由于没有电流通过，磁感应强度较小，电枢后端开口位置磁感应强度最大，达到23 T。随着脉冲电流的增大，枢轨的电流密度与磁感应强度也会相应增大。

4.2 瞬态温度场仿真计算

4.2.1 温度场数学模型

在电磁发射过程中，轨道表面温度迅速升高。若忽略轨道的对流传热和辐射传热，仅考虑轨道的热传导时[17]，轨道传热方程为

(9)

式中：T为温度；ρ为质量密度；Cp为比热容；k为热导率；Qj1为电磁-温度耦合得到的电流焦耳热；Qj2为枢轨接触面间产生的接触电阻热；Qf为滑动摩擦过程中产生的摩擦热。

根据式(9)，在温度场中同时加载Qj1、Qj2、Qf热源，可以得到轨道瞬态温升分布特性。

4.2.2 导轨瞬时温升分析

在电磁-温度耦合场下，利用载荷传递的方法，把通过瞬态电磁场获得的焦耳热以及计算所得的接触电阻热与摩擦热作为热载荷加载在温度场模型上，对轨道进行电磁-温度耦合仿真计算，并按3.1节对轨道进行分段研究。由于外轨未与电枢进行接触，外轨上只有电流产生的焦耳热且分布均匀，并且发射过程时间很短，主轨和外轨来不及进行热交换，故只针对主轨和电枢的接触面进行瞬时温升分析。图12为电枢出膛时刻沿电枢发射方向主轨道表面温度曲线(曲线上的点为不同段轨道表面的最高温度)。

通过对比图12中两条温度曲线可知，轨道在总热载荷的作用下炮尾位置温度最高，达到620℃；轨道在接触电阻热和摩擦热的作用下温度峰值为118℃，最高温度出现在接近轨道中部位置；轨道在电流焦耳热的作用下温度峰值为553℃，最高温度出现在炮尾位置。

从图12中可以发现，在总热载荷的作用下，轨道位置出现了两次温度峰值，第一次峰值出现在电枢运动初始阶段，主要原因是电流焦耳热在炮尾处不断累积，这种低速度、大电流的状况容易使轨道发生严重的烧蚀，进而引起转捩发生；随着电枢运动速度的增加以及接触压力的增大，累积的摩擦热和接触电阻热导致枢轨接触面温度再一次明显上升；随后至电枢出膛阶段，脉冲电流减小，枢轨接触压力变小，接触电阻热量和摩擦热量减少，轨道温度迅速降低。

4.2.3 发射后的冷却过程

电枢出膛后，为了更好地了解轨道在空气中的自然冷却过程，设置传热系数h=10 W/(m2·℃)进行模拟仿真。由于考虑接触电阻热和摩擦热更接近轨道炮实际发射情况，所以对轨道冷却过程的计算分析均已考虑接触电阻热和摩擦热。电枢出膛0.3 s后增强型电磁轨道炮轨道温度分布云图如图13所示。

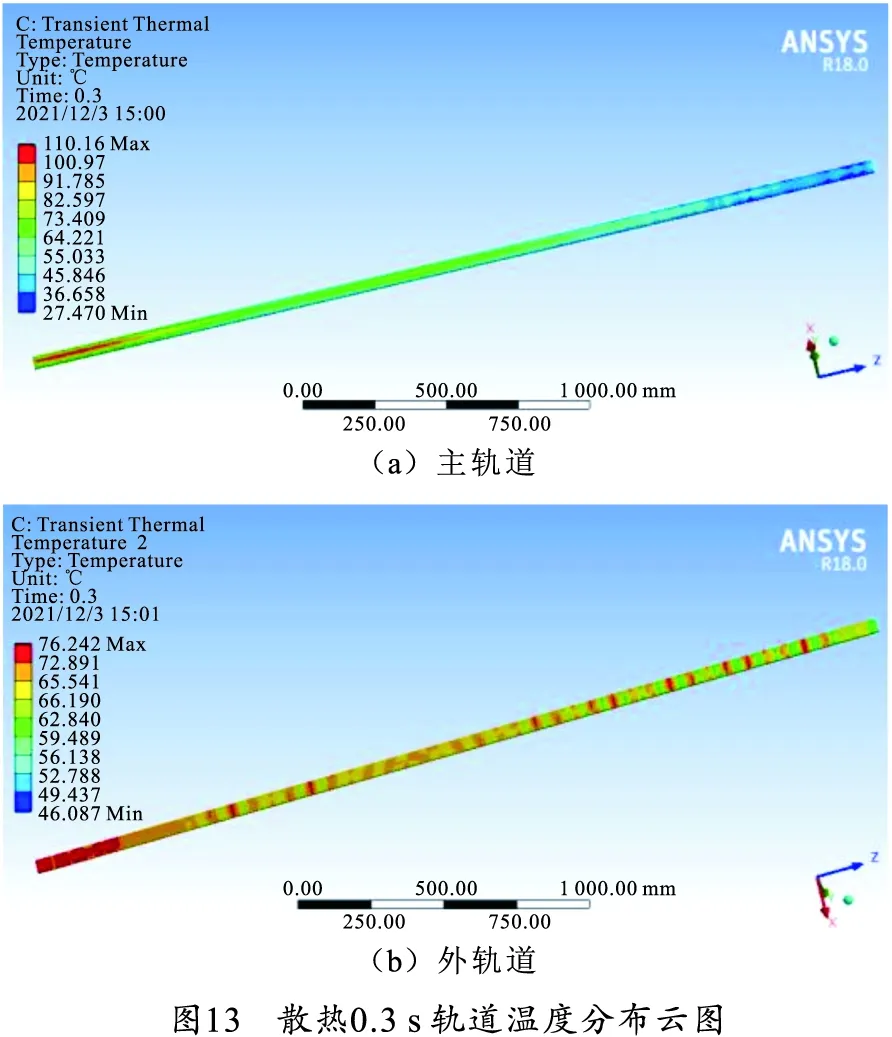
电枢出膛6 s后增强型电磁轨道炮轨道温度分布云图如图14所示。

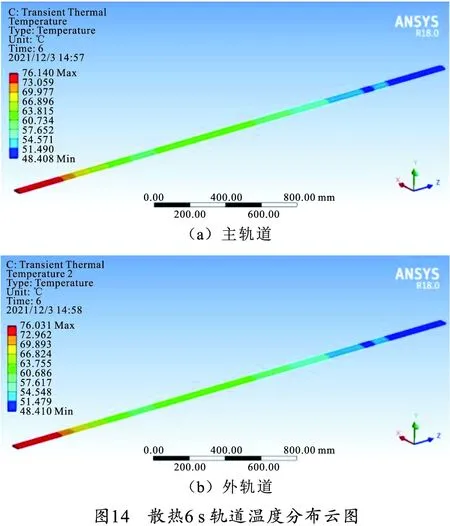
通过分析图13、14可知，散热0.3 s后由于铜轨道的导热性能很好，轨道表面的温度迅速降低，主轨与外轨温升分布不同，主轨表面温度较高。散热6 s后主轨与外轨达到热平衡状态，轨道表面温度梯度降低。

在脉冲电流流经简单轨道炮(2根轨道)时，轨道炮损耗和相同电流流经增强型电磁轨道炮(4根轨道)的损耗是不同的，在散热过程中传热途径也会有所不同。在初始条件均相同的情况下，电枢出膛6 s后简单轨道炮(轨道与增强型电磁轨道炮主轨相同)和增强型电磁轨道炮主轨表面的温度变化如图15所示。

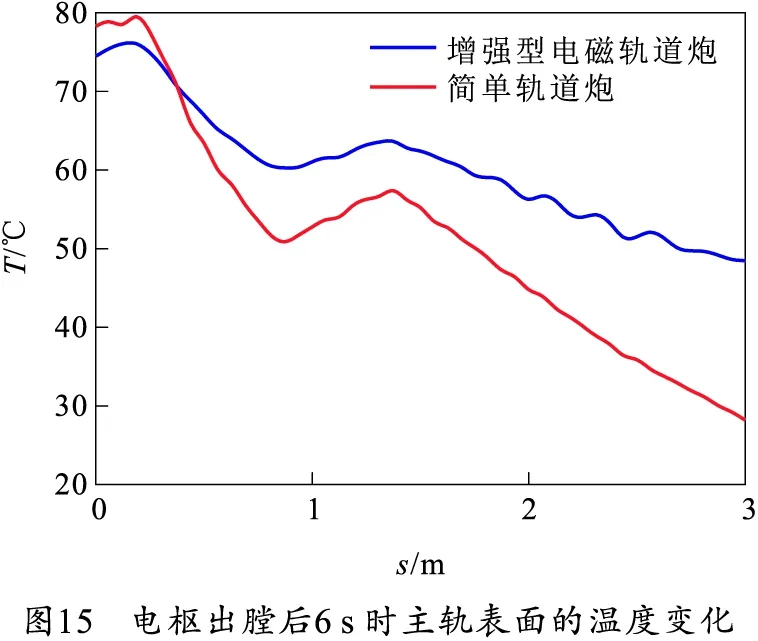
在初始条件均相同的情况下，电枢出膛6 s后，相比简单轨道炮，增强型电磁轨道炮主轨炮尾位置温度降低，炮口位置温度升高，主轨表面温度梯度降低，说明在相同冷却时间下，增强型轨道炮导轨与简单轨道炮导轨散热速度不同，增强型轨道炮导轨温度梯度较低。

4.3 瞬态结构场仿真计算

4.3.1 结构场数学模型

增强型电磁轨道炮的轨道主要承受垂直于轴线的横向力作用，以弯曲变形为主。在该方向上轨道受到的电磁力主要有主轨的电磁扩张力、外轨的电磁扩张力以及主轨与外轨之间的电磁力，可以将主轨与外轨简化为Bernoulli-Euler梁进行计算，将封装外壳化作弹性支撑。在电枢高速运动过程中，轨道的动力学控制方程为[8]

(10)

式中：w(x,t)为轨道横向变形量；ρ为轨道材料密度；A为轨道的横截面积；E为轨道材料杨氏模量；Iy为轨道横截面的惯性矩；k为弹性支撑的弹性系数；q(x,t)为轨道受到的载荷。

4.3.2 结构场计算结果

导轨结构形变会影响电枢的出膛速度以及能量转换效率，为了研究电磁力、焦耳热、接触电阻热和摩擦热共同作用下对轨道形变的影响，对导轨的瞬态扩张量分布情况进行计算分析。为了节省计算机资源，对电磁-温度-结构耦合模型进行以下假设：

1)采用顺序耦合法，忽略导轨形变对电磁场和温度场的影响；

2)忽略电枢运动过程中产生的电弧现象。

笔者对主轨与外轨进行电磁-温度-结构场耦合仿真计算，并按3.1节对轨道进行分段研究。运用有限元软件ANSYS Workbench，在电磁-温度-结构耦合场中，将电磁场模型导入到结构场，轨道材料为铜合金，电枢材料为铝合金。计算模型由六面体网格组成，包含4 379个单元，28 137个节点。将电磁场与温度场仿真结果作为载荷导入到结构场中，并设约束条件为轨道外侧面固定，将封装结构用弹性约束代替。这里将主轨与外轨在电磁力与温度场共同作用下的变形进行分析。在耦合全部热载荷、只耦合焦耳热和未耦合热载荷(只有电磁力)3种情况下，轨道扩张量最大值随电枢位移变化的对比如图16所示，轨道炮尾位置在扩张量峰值时刻的总形变云图如图17所示。

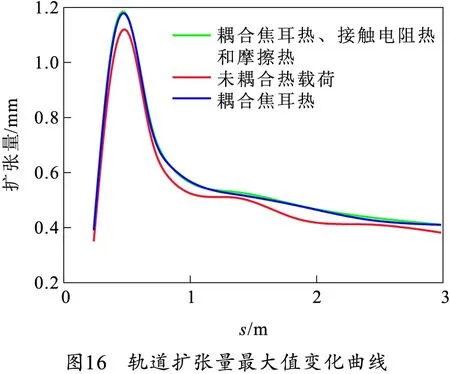
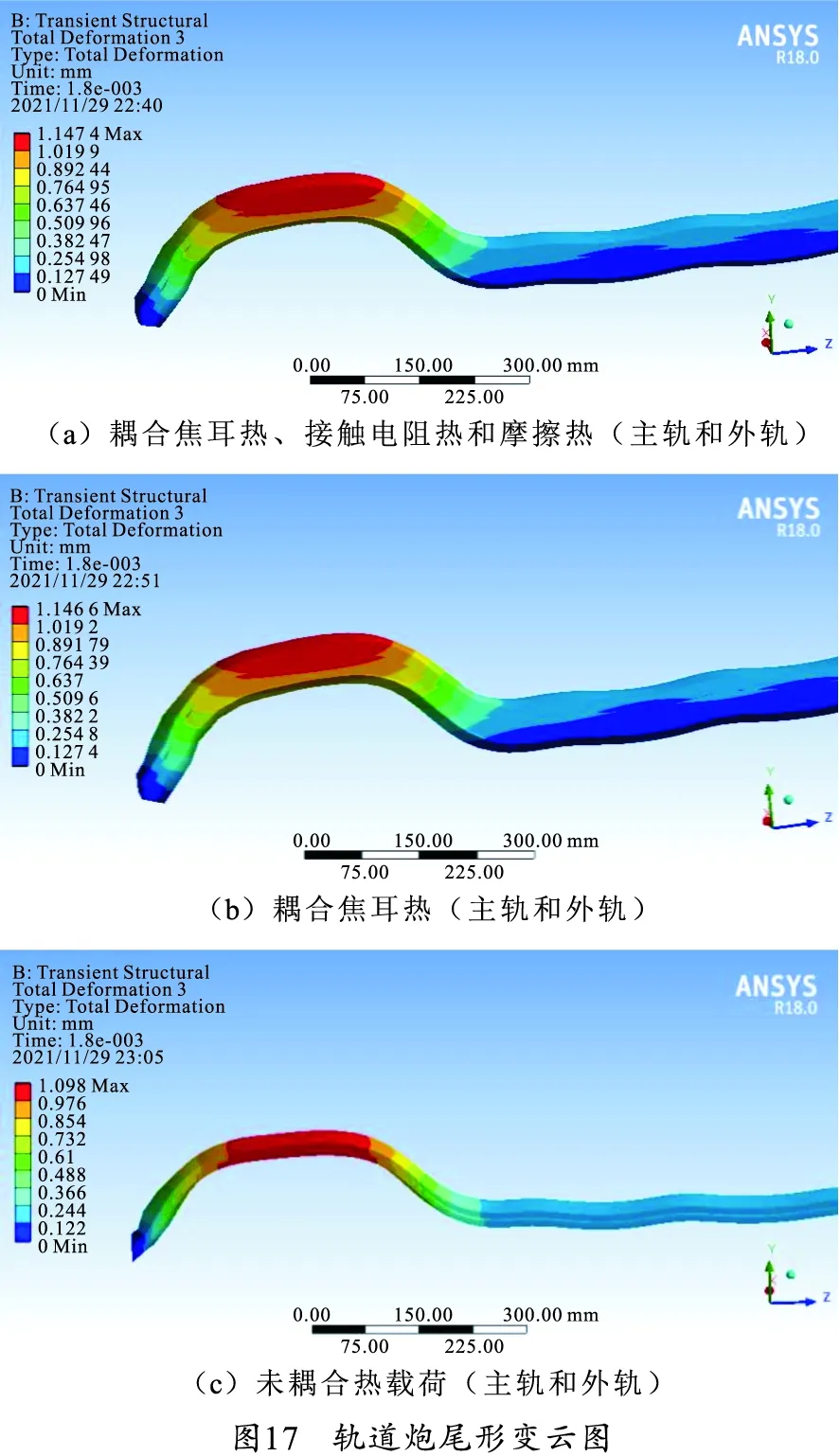
由图16、17可知，是否耦合温度场对轨道扩张量变化趋势影响不大，但是对扩张量数值有一定影响，在轨道扩张量峰值时刻，耦合全部热载荷扩张量为1.147 mm，未耦合热载荷扩张量为1.098 mm，轨道扩张量相差4%。在不考虑接触电阻热和摩擦热的情况下，只耦合焦耳热的轨道扩张量峰值为1.146 mm，与耦合全部热载荷结果相差不大。可见轨道扩张量主要是由电磁力引起的，考虑焦耳热后扩张量发生了变化，但变化不大。接触电阻热和摩擦热对轨道扩张量基本没有影响。

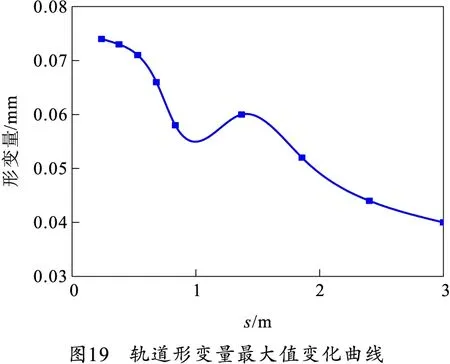
为了验证以上结论，分析了只考虑热应力情况下引起的热形变。将4.2.2节的瞬时温升分析结果(主轨考虑接触电阻热和摩擦热)作为载荷传递到结构场进行仿真，可以得到轨道的热应力以及热变形情况。轨道热应力最大值随电枢位移变化曲线如图18所示，曲线上的点为电枢运动到不同段轨道时轨道所受热应力的最大值。由热应力引起的轨道最大形变量随电枢位移变化曲线如图19所示。

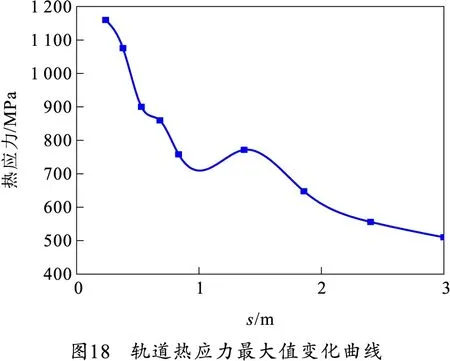
由图18可知，轨道热应力最大值变化曲线与轨道瞬态温度变化曲线的变化趋势相似，在电枢运动初始位置处热应力最大，最大值为1 160 MPa。轨道热应力峰值超过了轨道材料屈服强度200 MPa，容易造成轨道表面的塑性变形，严重时可能引起轨道表面产生裂纹，影响轨道使用寿命。

由图19可知，由热应力引起的轨道最大形变量出现在电枢起始位置，大约为0.075 mm。相比由电磁力引起的轨道形变量来说，热应力引起的轨道形变量较小。

5 结论

在本文的计算模型中，通过对轨道的分段研究，并且考虑接触电阻热量和摩擦热量的瞬态特性，给出了电磁发射过程中主轨与外轨的温度、扩张量的动态变化过程，提高了轨道瞬态温升分布和瞬态扩张量分布预测的准确性，可为增强型电磁轨道炮的设计提供参考。通过对轨道不同物理场问题的讨论，得到以下结论：

1)电枢出膛后，主轨整体温度分布不均匀，轨道最高温度区域出现在炮尾阶段。因此，需要对轨道炮尾处加强热管理。

2)在电枢发射过程中，轨道表面温度主要是由电流焦耳热引起的，随着电枢的运动，累积的摩擦热和接触电阻热也会影响轨道的温升分布。

3)在相同冷却时间下，相比简单轨道炮导轨，增强型电磁轨道炮导轨温度梯度较低。

4)在电枢发射过程中，轨道扩张量主要是由电磁力引起的，热应力引起的形变量较小。

笔者在计算热源项时，忽略了滑动电接触过程中产生的电弧现象。下一步的研究重点是将电枢运动过程中产生的电弧热源项、接触电阻热源项与摩擦热源项一起加载到不同物理场的计算中，以进一步提高轨道瞬态温度和瞬态结构模型的准确性。