基于有限元模拟的微电磁继电器的结构优化设计与研究

冯波，栗保明

(南京理工大学 瞬态物理国家重点实验室，江苏 南京 210094)

电磁继电器是一种电子控制元器件，具有控制系统(又称为输入回路)和被控制系统(又称为输出回路)，本质上是用较小的电流去控制较大电流的一种开关，可以在各种电路中有调节、转换、保护电路的作用[1-2]，被广泛应用于工业生产制造和自动化控制(比如航空航天系统、芯片制造、交通等)领域。最近几年微机电系统(MEMS)技术的研究与发展受到了极大的关注，以此技术为基础研制的微电磁继电器的前景也越来越广阔。和传统电磁继电器相比，微电磁继电器继承了它们的优点，比如性价比高，价格低，活动电极与固定电极接触电阻比较小，各组件耐压强度较大等，还有载流能力较强的优势，而且各个方面尺寸微小，那么在微执行通信等领域的应用就成为了可能，良好的集成性可以运用在各种各样的控制系统中[3-5]，比如火炮发射的伺服控制系统等。

笔者基于已有的微电磁继电器的研究，建立了微电磁继电器的结构模型，使用有限元模拟分析(ANSYS)软件和Origin图像处理软件对继电器线圈电磁场的分布情况和衔铁在平面磁芯线圈的电磁场中受到的电磁力进行仿真计算、结果处理[6-7]，为线圈中的电流激励、衔铁的使用材料，以及衔铁和固定电极的相对位置、各间隙大小设计奠定基础。对微电磁继电器的进一步应用具有一定的参考意义。

1 微电磁继电器的结构和工作原理

目前来讲，微电磁继电器通常是由平面磁芯线圈、绝缘层、导磁体层、衔铁、固定电极和硅基底等构成[8]。当微电磁继电器在实际使用环境工作的时候，在平面磁芯线圈中会施加电流激励，之后在平面磁芯线圈中就会发生电磁感应效应。衔铁这时自然受到平面磁芯线圈电磁力的吸引就会克服安装在电极之间的弹簧的弹力(相对传统继电器，弹力较小)被吸向固定电极，从而使得控制电路实现控制工作电路的目的。当平面磁芯线圈失去电流激励以后，由于返回弹簧的存在，衔铁就会返回。经过这样的流程，最终实现电路的闭合和断开。其中平面磁芯线圈是微电磁继电器的重要组成部分，线圈的材料、衔铁的材料、各个部分的结构和性质、各激励参数须满足以下条件[9-10]:

1)衔铁与固定电极的相对位置，即活动间隙需在微米量级内，而且各组件应该具有比较高的耐压强度，避免击穿。

2)在接触电阻很小的前提下，线圈需要提供稳定持续的接触力，才能使得工作电路一直保持闭合状态，比如当继电器工作在火炮发射等比较恶劣、复杂多变的环境中时，稳定的接触力能够保证继电器的可靠性。

3)在保证平面磁芯线圈的磁场强度满足实际各种需求的情况下，尽量提升线圈的载流能力，以满足实际运用中某些伺服控制系统的需求。

2 仿真结果分析与讨论

从目前的研究来看，研究微电磁继电器工作时，平面线圈内部和附近的电磁场分布，以及衔铁在平面磁芯线圈中因电磁感应效应所产生的电磁场中所受电磁力情况并对受力应变进行分析，对于确定在实际用途中电流激励的大小、各个电极的相对位置、触点分布、材质、各部分间距等参数，进而设计出稳定可靠的微电磁继电器具有十分重要的意义。

使用ANSYS有限元模拟分析软件和Origin图像处理软件对提出的微电磁继电器结构中的关键组件(平面线圈)的电磁场分布和衔铁在平面磁芯线圈中因电磁感应产生的电磁场中所受到电磁力的情况进行计算分析以及受力应变进行分析，综合考虑各种因素后，可以据此设计出比较合理的微电磁继电器结构的方案，为将来运用到火炮发射控制工程领域奠定基础。

2.1 平面磁芯线圈的电磁场分布

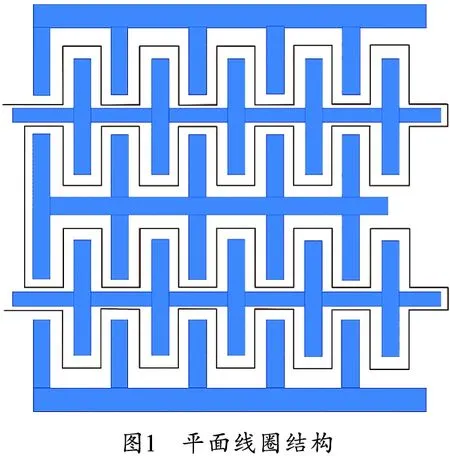
通过对目前微电磁继电器线圈结构的研究进行分析，可以考虑将平面磁芯线圈的结构制作成图1所示的结构(内部存在多处弯曲)。微电磁继电器其余部件的位置、结构如图2所示，副磁线圈位于主线圈间隙中。

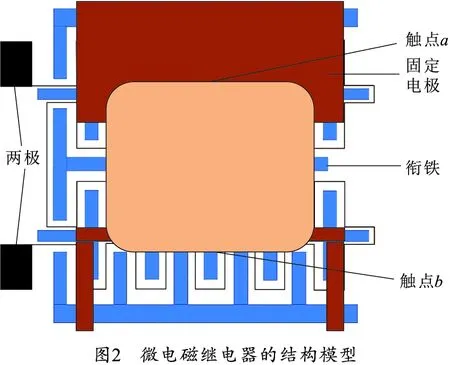
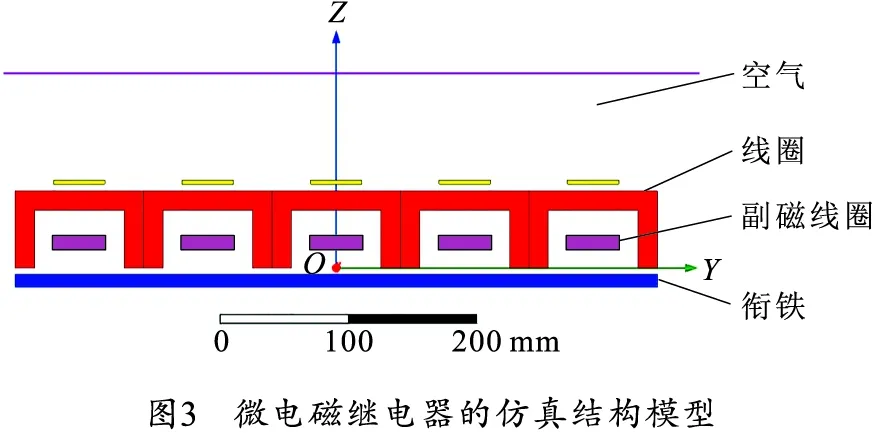
由于所给电流激励在单次计算中是稳定不变的，据此对微电磁继电器建立了如图3所示的3D稳态仿真模型，整个仿真模型大致由衔铁(由蓝色区域对应表示)、线圈(由红色区域对应表示)、副磁线圈(由紫色区域对应表示)和空气(由空白区域表示)4个部分构成。

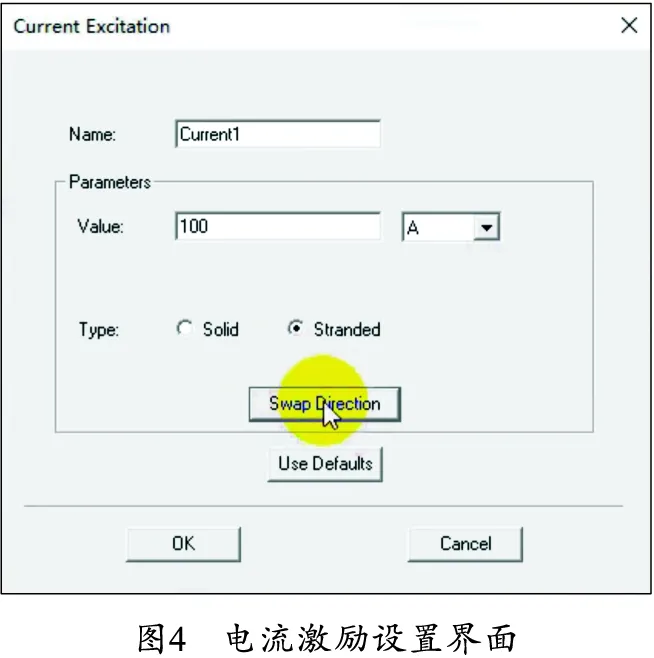
有限元分析电流激励设置大致如图4所示，所加电流激励为多匝Stranded类型，大小可以调整，激励位于线圈截面处。边界条件是默认的零磁场，故不需要再手动添加。

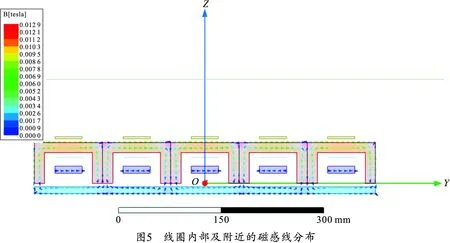
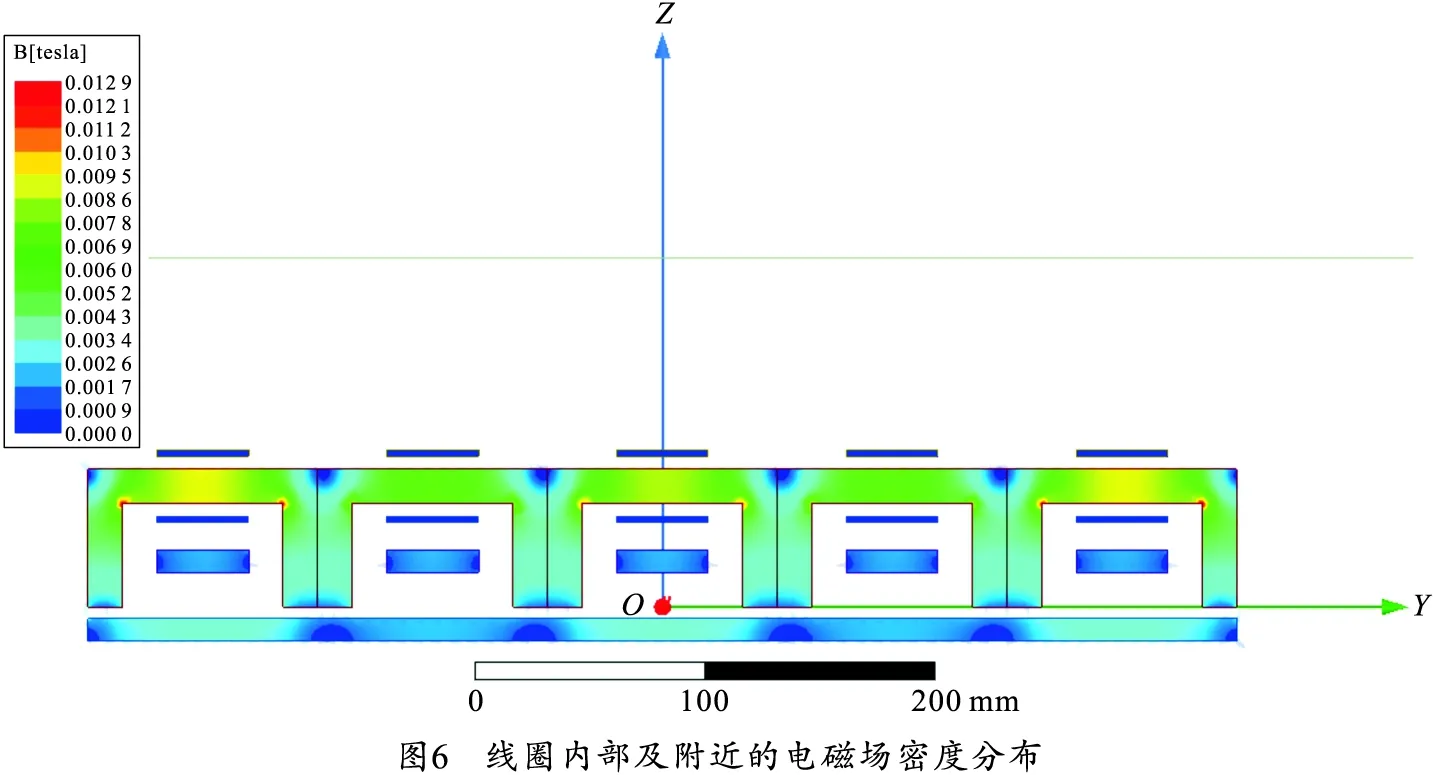
线圈内部及附近的磁感线分布和电磁场强度云图如图5～6所示。从仿真的结果可以得出结论，当线圈加上电流激励之后，发生电磁感应效应，由此产生一定的磁通量，磁通量主要集中在线圈内，通过间隙沿下部磁芯流入到附近的外磁芯，逐渐向其余外磁芯传播，从而产生了电磁吸引力作用在衔铁上，随后衔铁与固定电极接触，将触点接通，达到控制电路的目的。从线圈磁场云图的结果可得：线圈中的磁场主要分布在线圈内部且较为集中，这会对衔铁产生比较大的吸引力，这与后续的计算结果相符合，电磁力呈现为Z轴方向且大小较为稳定，其他方向的力与Z轴相比数量级相差过大，可以忽略不计，该吸引力能够保证衔铁和固定电极的稳定接触，提高继电器在工作时的可靠性，使其可以在复杂多变的环境下稳定工作。由此可以说明所建立的微电磁继电器的仿真模型是合理的。

2.2 励磁线圈的电磁力计算

当在平面磁芯线圈上施加激励时，产生电磁感应效应，衔铁会在线圈所生成的磁场洛仑兹力的作用下垂直运动下去。很明显，为了保证动静触点的接触，保证继电器工作的可靠性，线圈因电磁效应所产生的电磁场应当足够吸引衔铁，使它与固定电极接触，使得控制电路接通。因此，励磁线圈的电磁力应达到一定的大小。为了便于分析，一般认为衔铁此时是各向同性的磁性材料，则衔铁在垂直方向(Z)上所受到平面磁芯线圈的电磁力可以表示为[11]

(1)

式中：Bz为控制电路接通以后，线圈中电磁感应强度在垂直方向上的分量；Mz为衔铁被整个磁化后的磁感应强度的垂直分量；V为衔铁的体积大小数值。由此，经过推导Mz表示为[11]

(2)

式中：Xm为各向同性的磁性材料磁化系数；ur和u0为衔铁材料的相对磁导率和真空磁导率的数值，均可查表；Hz为线圈电磁感应磁场强度的垂直方向(Z)的分量。将式(2)代入到式(1)，可推导得

(3)

由毕奥-萨伐尔定律可知，磁感应强度是电流密度和距离的函数关系，以控制电路载流电流10 A为例，根据仿真计算结果，对电流进行参数化扫描处理，可得到不同电流下电磁力，如表1所示。

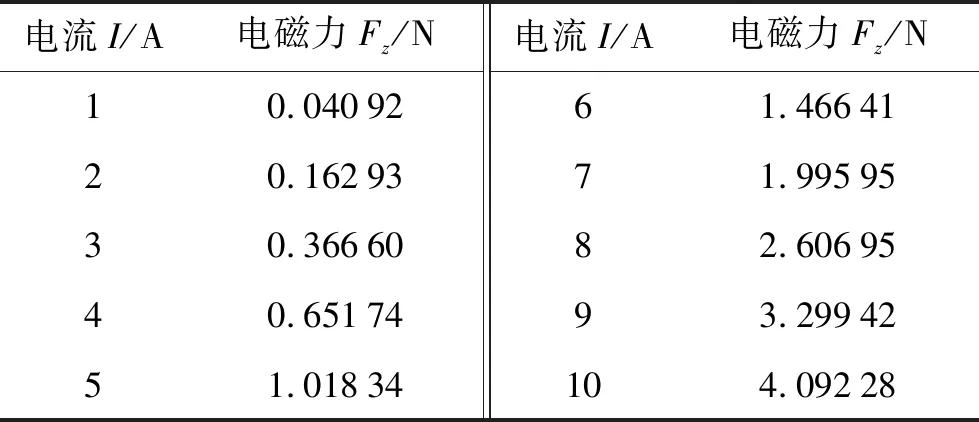
表1 不同电流下电磁力

由表1可知，对应电流激励下的电磁力方向呈现为Z轴方向，大小较为稳定且随电流变化呈现出一定的规律，这与前面的云图结果一致。利用Origin图像处理软件作出固定电极与活动电极间隙D为5 μm时的Fz-I函数图像，如图7所示。

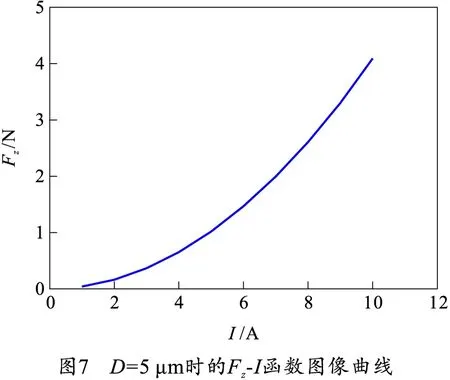
由图7可以看出，当电流激励增加，电磁力增长非常快，因此增大电流的激励可以促进衔铁和固定电极的闭合，使得控制电路接通，有助于提高继电器工作灵敏性，不过另一方面盲目增加电流也会让平面磁芯线圈的功率变得过大，可能出现异常发热、冒烟等问题，引发事故，降低可靠性，因此，在实际应用中线圈电流应控制在合理范围内，在同样的电流激励下，也可以考虑通过其他方式达到增强电磁力的目的，比如增加线圈匝数等。

同理，在线圈仿真结果中对活动间隙进行参数化扫描处理，可得I=10 A时的Fz-D函数图像曲线，如图8所示。

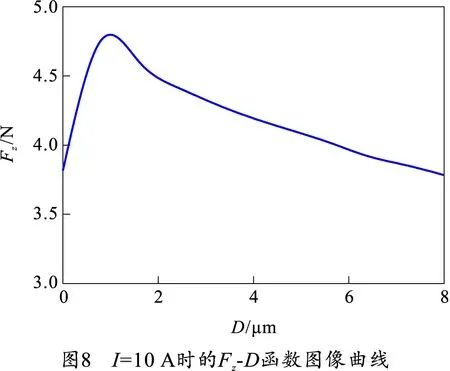
由图8可知，在线圈电流为10 A时，活动间隙约在1.2 μm处电磁力达到最大值4.8 N。可见，为保证电极间存在足够的吸引力，活动间隙的大小也应维持在合理的范围内，在当前参数下，活动间隙保持1.2 μm时继电器接通效果最好。

因此，为使继电器实现较为良好的控制效果，在设计器件结构与工作参数时，应该将励磁电流的大小、衔铁和固定电极的相对位置，还有平面线圈的功率大小等诸多方面的因素一起考虑。

2.3 衔铁的受力应变分析

对活动电极进行受力分析时，可以把电极看作悬臂梁模型来处理，假设电极各个部分受力都是均匀的，那么可以建立电极在垂直方向上的挠曲线方程[12-13]:

(4)

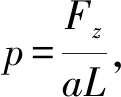
查阅资料，将衔铁材料的杨氏模量参数E=210 GPa，以及上面仿真过程中的参数和结果I=10 A，D=1.2 μm处的Fz代入到式(4)，通过Origin图像处理软件可得到衔铁在垂直方向的位移W和x的函数图像，如图9所示。

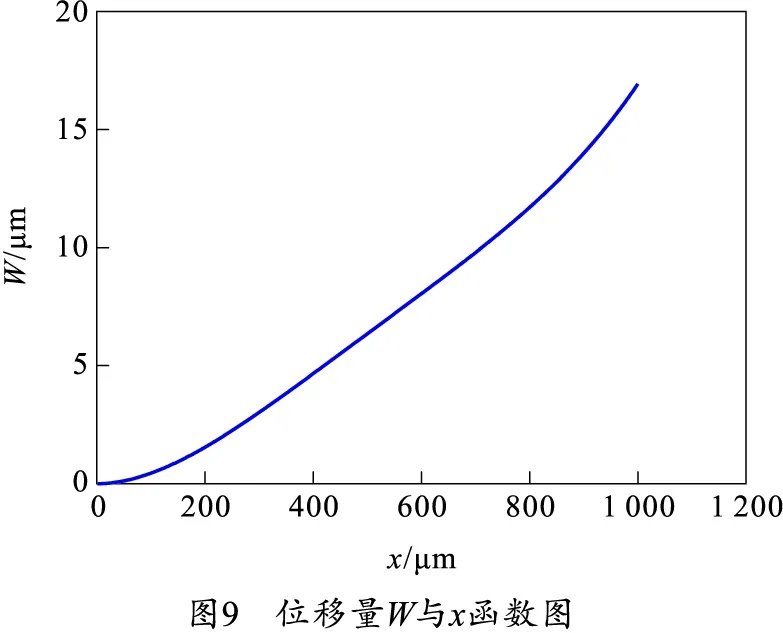
曲线在开始时上升趋势比较平缓，之后则是近乎线性上升。在x=L处，活动电极取得最大位移量为

可见，该参数下活动电极(衔铁)的最大位移量Wmax大于衔铁和固定电极的活动间隙D=1.2 μm，因此该参数下平面磁芯线圈对活动电极的电磁力足够吸引活动电极做往复垂直运动，继电器可以正常工作。结合电流与电磁力的关系，可以适当减小电流，这样可以兼顾不使线圈功率过大，增强继电器的可靠性，亦可产生足够的位移量，能提供足够稳定的接触力，如此继电器的结构得到进一步优化。

3 结束语

随着微电磁继电器技术的持续发展，其被逐步运用于芯片制造、航空航天和工业自动化生产等诸多领域中，前景变得越来越广阔。笔者主要针对微电磁继电器的结构和工作原理，使用ANSYS有限元分析软件仿真计算了继电器平面磁芯线圈内部和附近的电磁场分布，衔铁与固定电极之间的电磁力情况，以及对电极的应力形变进行分析，为微电磁继电器的设计提供依据，使微电磁继电器的结构得到一定的优化。