考虑退化特征相关性的火炮身管可靠寿命预测

纪超，吕卫民，张超

(1.海军航空大学 岸防兵学院，山东 烟台 264001；2.中国人民解放军66172部队，河北 石家庄 050200 )

现代火炮是战场上应用广泛的骨干常规武器，而火炮身管是决定火炮性能的关键部件。在火炮射击的过程中，火药燃气和弹丸弹带反复地对身管内膛造成烧蚀冲刷和机械磨损，导致其结构遭到破坏，影响火炮的射击性能，增大了安全事故发生的概率[1]。因此，研究预测火炮身管可靠寿命，对于指导基层部队科学管理装备、制定针对性维修保养计划以及降低实弹射击的安全风险等方面具有重要意义[2]。

目前身管寿命预测主要有基于理论推导和基于退化数据外推两类方法，二者中以基于退化数据预测的相关研究较多[3]，但基于退化数据预测方法主要集中在单退化特征的分析研究上，而身管在射击过程中伴随着复杂的物理和化学变化，存在多个性能特征同时退化的情况，单一退化特征难以全面精准地反映身管的实际工作状态，并且各退化特征之间通常是相关的，将其假设为线性相关或者多元正态分布，又不符合实际情况，因而有必要研究基于多元性能退化特征的身管可靠寿命预测方法[4]。

笔者以提高身管寿命预测精度和基层部队可操作性为目标，在考虑退化特征相关性的基础上，提出了基于二元Wiener过程的火炮身管可靠寿命预测方法。首先利用随机Wiener过程描述身管退化过程中的个体差异和非单调性，建立身管内膛磨损和弹丸初速的退化模型，采用基于Bayesian更新的EM算法识别模型中的未知参数；之后利用Copula函数描述它们之间的相关关系，建立考虑多个退化特征的退化模型，为综合评估火炮身管可靠寿命提供参考依据。

1 基于Wiener过程的退化建模

1.1 随机效应Wiener过程的退化模型

假设身管在退化过程中，各性能退化特征表现出非严格的单调递增(或递减)且观测时间一致，则可以利用随机Wiener过程进行建模分析。其第i个特征的退化模型可表达为

X(i)(t)=X(i)(0)+λ(i)t+δ(i)B(t)，

(1)

式中：t表示射弹数；X(i)(t)表示在射弹数为t时第i个性能退化特征量；λ(i)表示第i个性能特征的漂移系数；B(t)为标准布朗运动；δ(i)表示第i个性能退化特征量的扩散系数。

上述退化过程{X(i)(t),t≥0}具有如下性质：

1)X(i)(0)=0;

2){X(i)(t),t≥0}具有平稳的独立增量；

3)任意时刻间的增量服从正态分布，即：X(i)(t+Δt)-X(i)(t)～N(λ(i)Δt,δ2(i)Δt)，根据维纳过程的定义，增量ΔX(i)(t)服从正态分布，再令Δt=1，就得到其概率密度函数为

(2)

可定义ω(i)为第i个性能特征的失效阈值，定义T(i)为第i个性能特征的失效时间，即

T(i)=inf{t:X(i)(t)≥ω(i)|X(i)(0)<ω(i)},

(3)

式中，inf表示下确界。

在身管退化过程中，若其性能特征变化的情况服从Wiener过程，则其寿命服从逆高斯分布。在得到Wiener过程模型中的参数λ(i)和δ(i)之后，即可得到第i个性能特征失效时间的概率密度函数和可靠度函数，分别为[5]

(4)

(5)

式中，Φ(·)为标准正态分布。

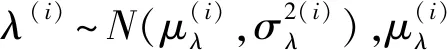
(6)

(7)

式中，p(i)(·)表示λ(i)的概率密度函数。

对应的剩余寿命分布函数为

(8)

1.2 基于Bayesian更新EM算法的未知参数估计

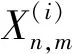
(9)

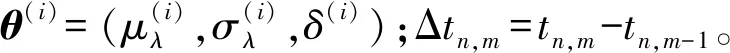
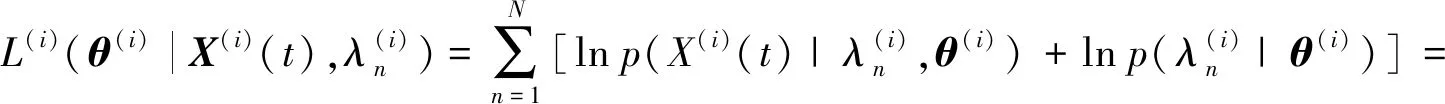
(10)

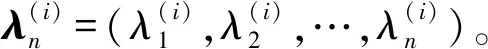
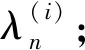
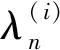
(11)

对比式(10)和式(11)可知：

(12)

(13)

将式(12)和式(13)代入式(10)中，可有E步如下：

(14)

M步如下：

(15)

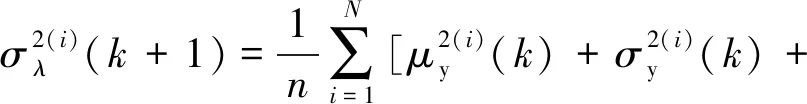
(16)

(17)

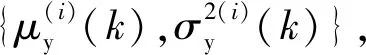
2 基于Copula函数的多元特征建模

2.1 Copula函数的基本理论

身管退化过程中，需要考虑不同性能特征之间的相关性，其中的机理较为复杂，相关系数的获取比较困难，采用协方差的方法确定其联合分布较为不妥，可引入Copula函数来解决这一问题。Copula函数能够描述各性能特征联合分布函数和边缘分布函数之间的关系，可以简化联合分布函数建模的复杂度，并提高相关性建模的可行性，如式(18)所示[9]：

H(X1,X2,…,Xn)=C(u1,u2,…,un;α)，

(18)

式中：H(X1,X2,…,Xn)表示各特征的联合分布函数；C(u1,u2,…,un;α)和α分别表示Copula函数和Copula函数中的参数；u1,u2,…,un表示各个特征的边缘分布函数。

2.2 常用的Copula函数及其选择标准

常用的Copula函数主要有Gaussian Copula、Frank Copula、Gumbel Copula和Clayton Copula等[10]，如表1所示。

表1 4种常见的Copula函数

可利用赤池信息准则(AIC)选择适合的Copula函数，其表达式为

EAIC=-2lnZ+2s，

(19)

式中：Z表示模型对应的极大似然函数；s为模型中的参数；EAIC值越小，说明模型的拟合程度越高。

2.3 相关多退化特征建模及可靠寿命预测

笔者选取典型的二元相关退化特征进行建模，并假设每个退化特征均服从前文所建立的随机Wiener退化模型。因此，联合分布函数可表示为

H(X1,X2)=C(u1,u2;α)，

(20)

对应的联合概率密度函数为

h(X1,X2)=c(u1,u2;α)·u1·u2，

(21)

式中，c(u1,u2;α)表示C(u1,u2;α)的概率密度函数。

由于式(21)只含有一个未知参数α，所以可采用极大似然估计法求解其估计值。

若身管两个特征中的任意一个先达到失效阈值时即认为身管失效，则身管的可靠度表示为[11]

R(t)=P(T>t)=P(min(T(i))>t)=P(T(1)>tT(2)>t)=1-P(T(1)≤t)-P(T(2)≤t)+P(T(1)≤tT(2)≤t)=R(1)(t)+R(2)(t)-1+Cα(u,v).

(22)

根据式(6)，可得到身管失效时间的联合概率函数：

(23)

3 实例分析

火炮身管退化失效的过程中主要有内膛烧蚀磨损、弹丸初速下降、最大膛压下降、射弹散布增大、弹带削光等表现。其中内膛烧蚀磨损是其失效的主要机理，弹丸初速和最大膛压下降等表现是由内膛烧蚀磨损引起的，因此内膛磨损量是身管性能退化的直接特征量，弹丸初速下降、最大膛压下降等表现是间接特征量[12]。两者在整个身管试验过程中都表现为退化，所以笔者采用内膛磨损和弹丸初速作为主要特征进行研究。实例的研究对象为某型号坦克炮身管，所选身管内膛磨损量的失效阀值约为4 mm，弹丸初速的失效阀值约为1 657.1 m/s。

为得到同类型身管的内膛磨损和弹丸初速数据，根据文献[2]的做法和文献[13]的数据，分别在内膛磨损量和弹丸初速值上叠加一组随机数(初始数值均为0)，以模拟同类型其他身管的性能退化情况，从而生成4组数据，退化趋势如图1所示。

由于样本数少于50个，所以采用Shapiro-Wilk正态性统计检验方法，对相等时间间隔内的每个身管样品退化量ΔX(i)(t)进行正态性检验，得到各组数据p′值，如表2和表3所示，由于篇幅限制，展示部分图像如图2所示。

表2 内膛磨损增量S-W假设检验结果

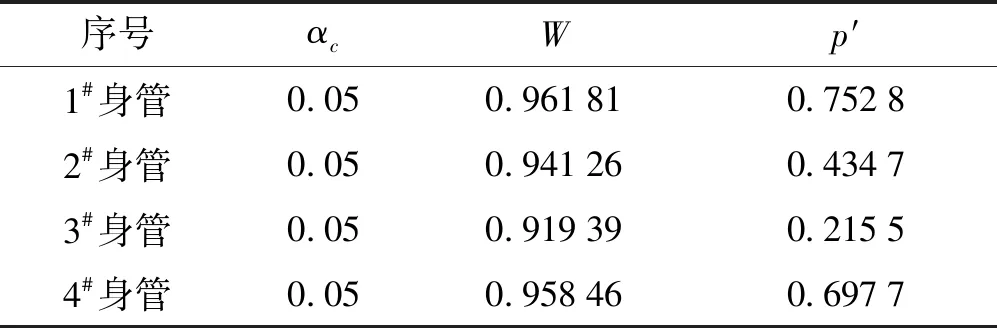
表3 弹丸初速下降增量S-W假设检验结果

由表2、3和图2可知，p>αc表示不拒绝退化特征增量为正态分布的原假设，因此两个性能退化特征增量都服从正态分布，故身管整个性能退化过程服从随机Wiener过程。

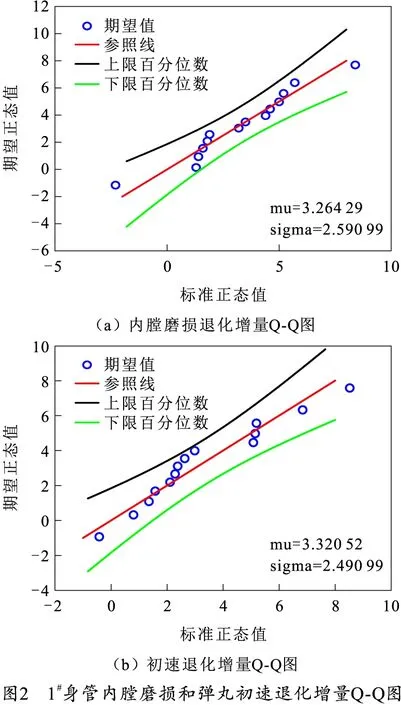
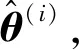
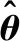
表4 未知参数估计结果

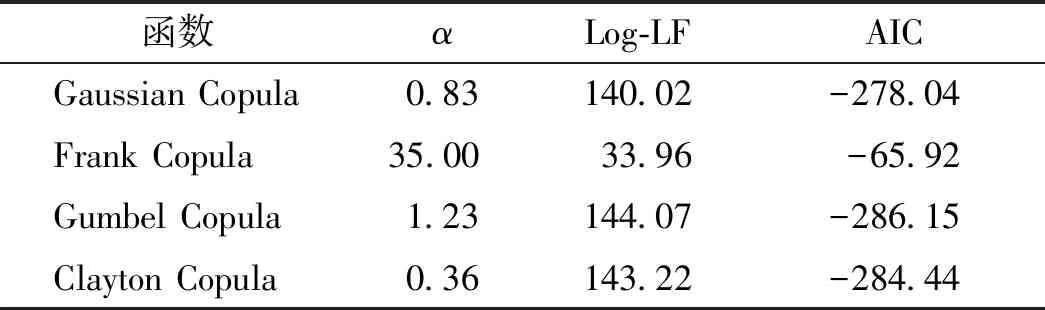
表5 各Copula函数参数估计值及AIC值

由表5可知，Gumbel Copula模型对应的AIC值结果最小，对二元相关退化特征的联合退化模型的拟合效果最好，因此采用Gumbel Copula函数描述身管两个性能退化特征之间的相关关系。

为验证特征相关性对可靠性和可靠寿命的影响，将式(1)表示的单一特征内膛磨损和弹丸初速度的寿命预测模型分别记为A1和A2，其可靠度和可靠寿命的计算公式分别为式(6)和式(7)；将未考虑样本差异的模型和本文所建立的模型分别记为A3和A4，其可靠度和可靠寿命的计算公式分别为式(22)和式(23)，结果如图3、4和表6所示。

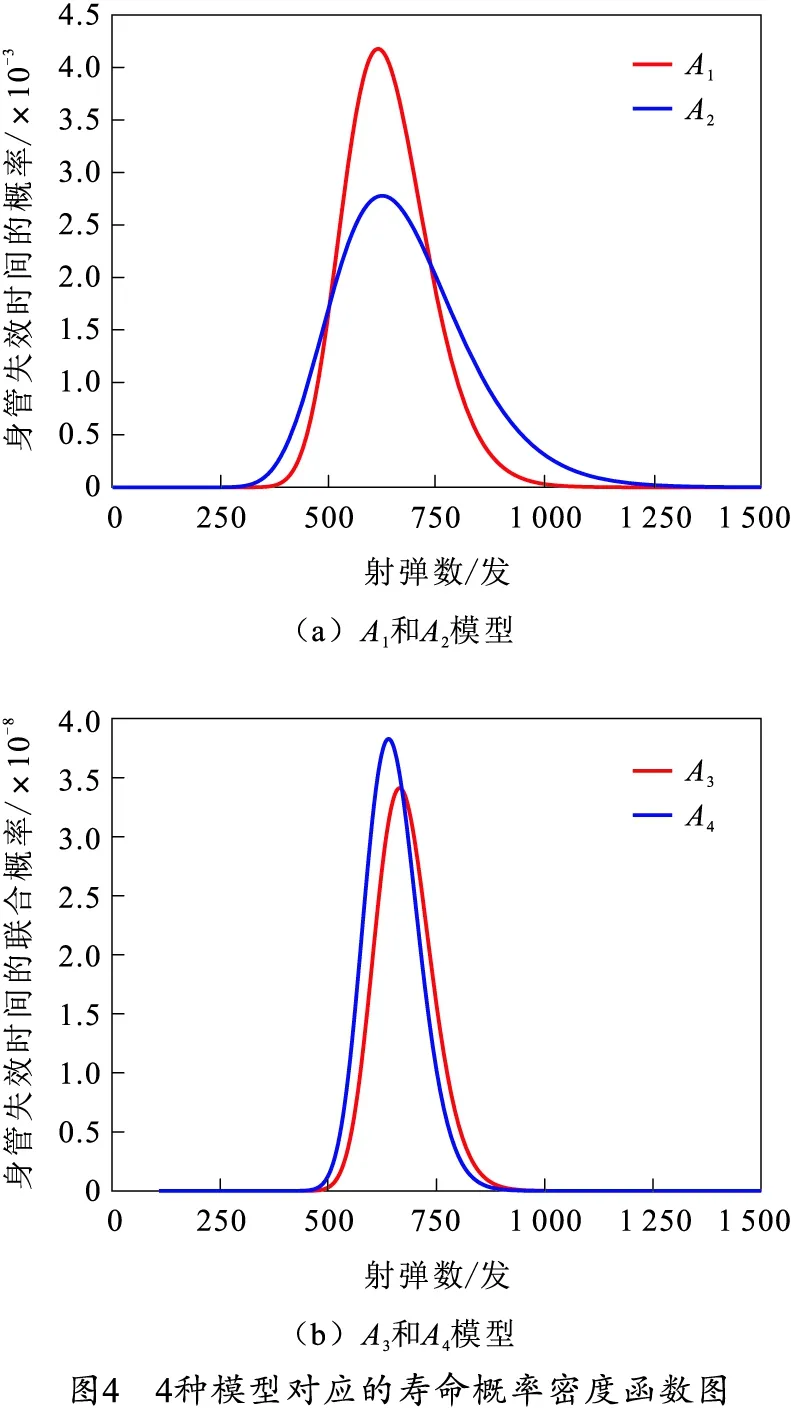
表6 4种模型的可靠寿命和中位寿命 发

由图3可知，4种模型在初期均保持着较高的可靠度，但是随着时间的增加，可靠度结果出现差异，考虑个体差异和特征量相关性的可靠度较为保守，而单一特征量和不考虑个体差异的结果在一定程度上会高估身管的可靠度。由图4可以看出，模型A1和模型A2对应的寿命分别在第615发和第627发左右达到峰值，而模型A3和模型A4对应的寿命分别在第630发和第650发左右达到峰值，而且寿命曲线较A1和A2显得“窄而高”，表明剩余寿命预测的不确定性较小，准确度较高。所以，仅靠单一特征量和单一样本难以完全反映出坦克炮身管的健康状态，因此，在身管可靠性评估和寿命预测中有必要考虑多个性能特征和个体差异。

若以中位寿命R=0.5时表示身管的可靠寿命，则经过计算得到寿命为588发；当可靠性在R=0.9时，对应的寿命为478发。因此根据可靠寿命预测结果，可以为身管的维护保养和修理更换提供理论依据。

4 结束语

身管性能退化中存在的个体差异，基于传统Wiener过程的模型已经无法满足对火炮身管可靠性评估要求。笔者通过引入随机参数的方法，利用随机Wiener过程分别建立了内膛磨损和弹丸初速度的退化过程模型，采用基于Bayesian更新的EM算法计算模型里的未知参数。从实例分析结果来看，考虑个体差异后，火炮身管的可靠度略低于传统方法。

目前较少有文献研究同时考虑火炮身管多个退化特征的情况。笔者提出了利用二元退化特征进行可靠性评估和可靠寿命预测的方法，利用Copula函数描述各退化特征间的相关关系，简化了联合退化特性分布函数建模难度，在一定程度上提高火炮身管寿命预测的精度，为实际火炮身管的可靠寿命预测提供了一定的参考价值。