基于位置关系模糊聚类的Web服务质量预测

随着面向服务计算的快速普及，Web服务的增长也变得十分迅速，因而在面对众多可以提供相似功能的Web服务时，如何能够让用户找到最佳的服务成为一个热门问题[1]。针对这个问题，引入服务质量(Quality of Service，QoS)的定义，QoS代表的是Web服务的非功能属性，如可用性、可靠性、响应时间、吞吐量、安全性和服务费用等[2]。因为这些属性可以很好地体现Web服务性能的差异化，所以在为用户进行服务推荐时常将其作为首要且重点考虑的指标。但在真实的情景中，用户所调用的服务只是众多Web服务中很少的一部分，这就导致了可供参考的用户历史QoS数据严重稀疏，因而根据已知的QoS历史信息对缺失的QoS数据进行预测成为服务推荐中的一个重要研究问题。

在Web服务质量预测的研究中，协同过滤(Collaborative Filtering，CF)[3]是一种常用的方法。Shao等[4]根据相似用户的已知QoS数据利用CF预测QoS。Zheng等[5]在考虑了请求用户的相似用户之外，还进一步挖掘了目标服务的相似服务，从而提出了混合CF预测QoS。以上两者均采用皮尔逊相关系数计算相似度，在面对数据稀疏问题时，相似度准确度较低。为此，申利民等[6]改进了相似度的计算方法，并且又考虑到用户调用服务的历史QoS数据之间存在的比率关系，以此来提高预测精度。此外，为了发掘历史QoS数据的潜在特征，唐瑞春等[7]基于信任度模型来寻找最佳的相似用户，再结合CF方法预测QoS值。以上学者只针对历史QoS数据进行了分析，忽略了用户与服务自身的内在特征，因而会存在一定的噪声数据影响QoS预测精度。因此，徐文庭等[8]针对噪声问题构建分类树，并基于同一分类集合使用Slope One算法进行预测。任迪等[9]将用户的IP地址、经纬度、所在国家等内在属性作为特征构建贝叶斯分类器，并将分类概率作为权重因子进行服务质量的预测。Chen等[10]提出了一种新的基于CF的Web服务QoS预测，利用位置信息和QoS历史数据对用户和服务进行聚类，并根据聚类结果对用户进行个性化的服务推荐。Liu等[11]提出同时利用用户和Web服务的位置来为目标用户或服务选择相似用户，并对用户和Web服务进行增强的相似性度量。鲁城华等[12]将Web服务的QoS信息与用户和服务的内在区域属性相结合，采用矩阵分解法构建预测模型。

由于用户与服务所在区域的不同，它们之间的网络情况也会存在差距，而网络因素对QoS的影响是客观存在的，但传统协同过滤只是单纯的考虑历史数据的相似性，并没有考虑用户与服务的位置相关性，因而会出现相似度计算不准确的问题。为进一步充分利用用户与服务的位置信息，并考虑到硬聚类算法的局限性(若聚类簇数过小，则聚类后同一簇之中簇的上界与下界会存在一定差距；若聚类簇数过大，则同一聚类簇中可用数据就会变少)，本文提出一种基于位置关系模糊聚类的Web服务质量预测方法：

(1)考虑到用户与服务之间因地理位置因素不同所造成网络环境的影响，本文根据用户与服务的内在经纬度特征数据，利用距离关系数据建立模糊C均值聚类模型，并根据得到的隶属度矩阵采用新的相似度计算方法计算位置关系上的相似度。

(2)针对传统相似度计算方法在数据高稀疏度的情况下精度较低这一问题，本文利用用户的历史QoS数据，采用一种改进的相似度计算方法计算用户或服务之间的相似度，并使用权值将用户或服务位置关系上的相似度与历史QoS相似度相融合，进而进行QoS的预测。

1 基于位置关系模糊聚类的协同预测方法

1.1 位置关系模糊C均值聚类算法

1.1.1 特征提取

本文所需要的特征，均由真实的数据集提供，其中用户与服务的内在信息包括：ID、IP地址、国家、大陆、纬度、经度等[9]，其中服务的经纬度特征为服务提供商所在的具体位置。在构建模糊C均值聚类模型前需要提取每个用户和服务的经纬度信息，以此来计算两者之间的距离。数据集提供的经纬度信息采用WGS84格式，其中北纬为正，南纬为负，东经为正，西经为负，具体见表1、表2。

表1 用户的位置信息

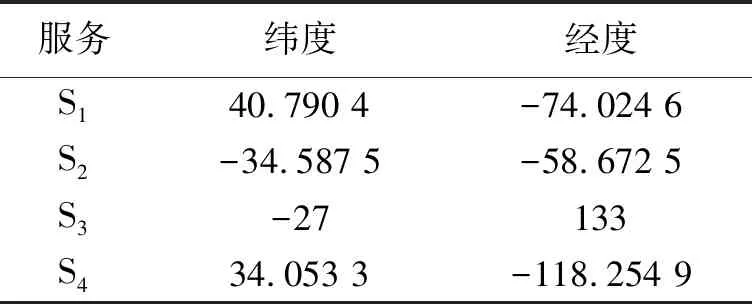
表2 服务的位置信息

1.1.2 计算(用户-服务)的位置关系

本文在计算用户与服务之间的位置关系时，根据数据集中提取的经纬度特征采用半正矢(Haversine)[13]距离公式计算用户到服务之间的距离，从而得到一个(用户-服务)的距离矩阵。半正矢公式为

(1)

其中r代表地球的半径，(la1，lo1)与(la2，lo2)分别代表需要计算距离的两个不同样本的(纬度，经度)。

根据得到的(用户-服务)之间的距离关系，生成可用于模糊聚类的数据集合L，具体见表3。

表3 (用户-服务)距离关系 km

1.1.3 模糊C均值聚类原理

算法原理：若将所给的n个样本数据集合x={x1，x2，…，xn}，聚类到k个不同的簇之中，需要将目标函数Jm不断进行迭代，从而使其最小化。目标函数Jm为

(2)

根据目标函数Jm，进行最优化求解，可得聚类簇中心cj与隶属度uij的表达公式：

(3)

(4)

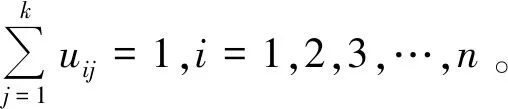
在聚类过程中需要引入一个阈值ε，并将其设置为聚类停止迭代的条件。具体迭代停止条件为

(5)

1.1.4 构建聚类模型，获取隶属度

通过1.1.1与1.1.2，我们已经将用户与服务的内在经纬度特征提取出来，并根据半正矢距离计算公式得到了(用户-服务)距离关系的数据集合L，因而可进行模糊C均值聚类算法模型的构建：

输入：(用户-服务)距离关系的数据集合L

过程：(1)选择合适的聚类簇数k及隶属度因子m；

(2)初始化簇中心cj、隶属度uij；

(3)通过不断迭代计算，更新隶属度uij与簇中心cj；

(4)当达到指定迭代停止条件时，完成聚类。

输出：隶属度矩阵U

因为在对QoS进行预测时，使用的是混合协同过滤算法，即使用一定权值融合基于用户与基于服务的协同过滤算法，那么在对位置关系进行相似度的计算时，也需要根据基于用户或基于服务分别进行位置关系上相似度的计算，以便融合混合协同过滤算法根据历史QoS数据计算的相似度。所以在构建模糊C均值聚类时需要分别对基于用户与基于服务进行模糊C均值聚类模型的建立，从而得到用户所属聚类簇的隶属度矩阵Ud以及服务所属聚类簇的隶属度矩阵Us。Ud与Us见表4、表5(此表作为示例，设置的聚类簇数为4)。

表4 用户的隶属度矩阵Ud

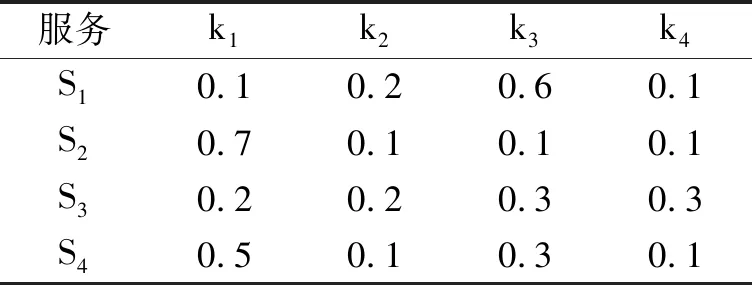
表5 服务的隶属度矩阵Us

1.2 协同过滤算法预测QoS

1.2.1 位置关系的相似度计算

考虑到传统聚类方法使得同一聚类簇中的边缘用户或服务的相似度存在一定差距，从而影响最终的QoS预测结果，根据模糊C均值聚类所得的隶属度计算，引入位置关系相似度的计算方法。由于在FCM模型中所得到的隶属度矩阵中每个用户都具有相同的维度，并且不存在缺失值，所以对其进行相似度的计算就不用担心数据稀疏性对精度所造成的影响。因而，本文提出一种改进的相似度计算方法，通过用户与服务的隶属度矩阵将比值相似度的计算算法与欧式距离的计算方法相结合，从而更加准确地计算用户和服务在位置关系隶属度上的相似度：

(6)

式中当max(xi，yi)=0时，说明最小与最大都为0，因而分式直接赋值为1。k代表的是聚类簇数即所得隶属度矩阵的维数。x与y分别代表请求用户或服务与其他用户或服务所属聚类簇的隶属度向量，并且根据计算不同对象的隶属度相似度时，x与y所属集合不同。当计算用户所在位置关系上的相似度时，x,y∈Ud，得到相似度SimUd。当计算服务所在位置关系上的相似度时，x,y∈Us，得到相似度SimUs。

1.2.2 历史QoS数据的相似度计算

由于在历史QoS数据稀疏的情况下，传统相似度的计算方法会因为共同调用服务数量过小而造成较大误差。因而本文提出一种改进的相似度计算方法，充分利用到已知的QoS数据计算与用户或服务之间的相似度，并给与拥有更多共同调用服务的用户之间的相似度更高的权值。在基于用户的协同过滤算法中，请求用户u与相似邻居用户v之间的历史QoS数据相似度的计算为

(7)

其中Su表示请求用户u调用过的服务集合，Sv表示相似邻居用户v调用过的服务集合，|Su∩Sv|表示请求用户u和相似邻居用户v共同调用过的服务个数，|Su|和|Sv|代表的是请求用户u和相似邻居用户v调用过的服务个数，qu,i为请求用户u调用服务i的QoS值，qv,j代表的是相似邻居用户v调用服务j的QoS值。

在基于服务的协同过滤推荐方法中，采用式(8)来计算目标服务s与相似服务w的相似度：

(8)

其中Us表示调用过目标服务s的用户集合，Uw表示调用过相似邻居服务w的用户集合，|Us∩Uw|表示共同调用过目标服务s和相似邻居服务w的用户个数，|Us|和|Uw|分别表示调用过目标服务s和相似服务w的用户数，qi,s表示用户i调用服务s的QoS值，qj,w表示用户j调用服务w的QoS值。

1.2.3 融合相似度

为了缓解因地理因素不同造成相似度计算精度的影响，通过设置权值α、β将用户和服务的位置关系相似度与历史QoS数据相似度相融合，用户或服务之间的相似度融合公式为

Simcd=αSimUd+(1-α)Simd,α∈[0,1]，

(9)

Simcs=βSimUs+(1-β)Sims,β∈[0,1]。

(10)

1.2.4 预测QoS

在分别计算用户和服务的位置关系相似度及历史QoS数据相似度并进行融合之后，通过混合协同过滤算法来预测请求用户调用目标服务的QoS值，并且在预测QoS值的过程中考虑到不同用户之间QoS值存在一定的比例关系[6]，使用其平均值的比值作为一定约束，使QoS预测值更加准确。

在基于用户的协同过滤推荐方法中，通过请求用户与相似邻居的相似度来预测请求用户u调用目标服务s的QoS值：

(11)

在基于服务的协同过滤推荐方法中，采用式(12)来预测请求用户u调用服务s的QoS值：

(12)

基于用户和基于服务得到的两个预测值具有不同的预测精度，使用两个置信权值conu和cons来平衡这两个预测值：

(13)

(14)

不同的数据集有其自身的数据分布特性，在使用置信权值来平衡之外，还需要加入参数λ(0≤λ≤1)来优化根据基于用户和服务得到的两个预测值的权重。根据得到的置信权值，用ωu和ωs作为权重因子融合基于用户和基于服务预测值，其中ωu+ωs=1，ωu和ωs的定义如下：

(15)

(16)

引入权重因子后，就来预测请求用户u调用预测服务s的QoS值：

(17)

2 实验结果

2.1 数据集

为了保证实验的真实可靠性，本文选择在真实的数据集上验证所提方法的有效性。本文使用的数据集为WS-DREAM公开发布的数据集Dataset Dream dataset2，该数据集记录了339名用户调用5825个Web服务的QoS值[15-16]，包括响应时间和吞吐量两个属性，其中响应时间范围为0～20 s，吞吐量范围为0～1000 kbps。本文针对响应时间数据进行实验分析，并在进行实验前需要删除服务中响应时间为-1，代表访问超时的服务。

因为本文需要研究在数据稀疏的情况下，所提方法对于QoS预测的精确度提升。但在原始的数据集中，已知的响应时间数据比较密集，因而需要对数据集进行稀疏化处理。本文将在85%、95%两种不同稀疏度下进行最优化参数实验，在80%、85%、90%、95%四种不同稀疏度下进行实验对比，从而验证所提方法的有效性。

2.2 评价指标

本文采用平均绝对误差(mean absolute error，MAE)[17]和归一化平均绝对误差(normalized mean absolute error，NMAE)[18-20]来衡量预测精度的评价指标。具体如公式(18)、(19)所示：

(18)

(19)

式中N表示预测的所有QoS的个数，Pu,s表示请求用户u调用服务s的实际QoS值，Qu,s表示请求用户u调用服务s的预测QoS值。

2.3 实验过程、参数设置及对比实验

在研究本文所提基于位置关系模糊聚类的协同预测方法(Collaborative prediction method based on fuzzy clustering of location relationship，CP-FCLR)时，需要对一些参数进行最优化选择。然后再将本文所提CP-FCLR方法与以下几种方法分别在不同稀疏度情况下进行实验对比：UPCC(采用基于用户的协同过滤算法预测QoS)、IPCC(采用基于服务的协同过滤算法预测QoS)、WSRec(采用混合协同过滤算法预测QoS)[19]、SVD[20](采用矩阵因子分解算法进行预测)、CACF[8](采用CART分类树与Slope One算法进行预测)、BBCF[9](结合贝叶斯分类器进行协同预测)，前三种方法均使用皮尔逊相关系数计算用户或服务之间的相似度。

2.3.1 融合权值α、β的最优选择及敏感性分析

为了研究相似度融合时，融合权值α、β对实验结果的影响、最优化选择及其在不同稀疏度情况下的敏感性分析，本文使用改进后的融合相似度计算方法分别在基于用户与基于服务的情况下进行实验。选取不同的融合权值α、β，分别在稀疏度为85%、95%的数据集上进行实验，根据评价指标MAE进行对比，从而选择最优权值。实验结果如图1、图2所示。

图1 稀疏度85%下α与β对MAE的影响 图2 稀疏度95%下α与β对MAE的影响

根据实验结果可以看出融合用户和服务的地理位置关系相似度可以在一定程度上提高相似度的准确性，也缓解了噪声数据对实验结果的影响，从而提高QoS的预测精度。并且，在不同的稀疏度下参数α与β的最优取值比较稳定，都在取值为0.4或0.5时，所得到的预测结果最优，并且在取值为0.4或0.5时得到的误差值相差很小，因而可以看出融合权值α、β的最优取值对于历史QoS数据的稀疏度不敏感。因此通过综合考虑，在本文后续的工作中将相似度的融合权值α与β设置为0.4。

2.3.2 不同Top-K对实验精度的影响

因为数据稀疏度的不同，在选择最近邻时，可供选择的近邻数也会存在较大差别(稀疏度越大，近邻数越少)。所以根据Top-K原则，本文在数据稀疏度为85%、95%的数据集下，分别选取不同的最近邻数K，根据评价指标MAE进行分析，从而选取最优的最近邻数K进行QoS预测。具体实验结果如图3、图4所示。

图3 稀疏度85%下近邻数K对MAE的影响 图4 稀疏度95%下近邻数K对MAE的影响

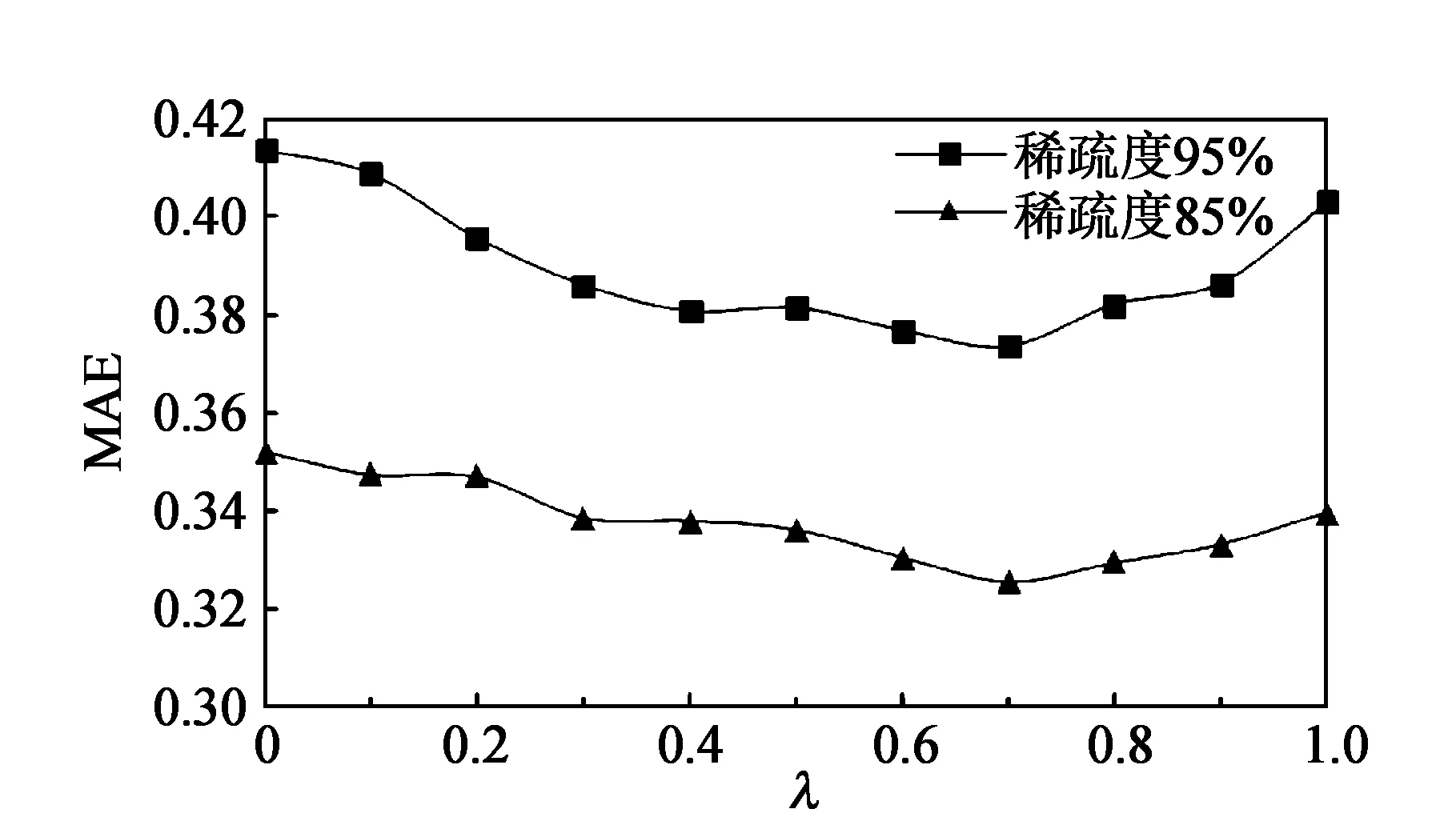
图5 不同λ对MAE的影响

2.3.3 不同λ值对实验精度的影响

为了能够更好地将基于用户的协同过滤与基于服务的协同过滤相融合，引入参数λ形成权重因子融合两种算法。为了选择最优的λ值，本文使用提出的CP-FCLR算法，在数据稀疏度为85%、95%的数据集下选择不同的λ值进行实验。

实验结果如图5所示，根据评价指标分析，在稀疏度85%、95%下，当λ取值0.7时，MAE最小，即所得实验结果最优。综合考虑，本文选择0.7作为λ的值。

2.3.4 不同稀疏度与预测样本数量下的预测精度与运行时间

在稀疏度为85%、95%的情况下，使用本文所提方法进行预测，设置待预测的样本数量分别为10、20、30、40、50，经过多次实验取其均值，分别得到评价指标MAE、NMAE及运行时间Time(单位：s)，所得实验结果见表6。根据实验结果可以看出，随着样本数量的提高，评价指标MAE、NMAE的值逐渐趋于平稳，从而证明了本文所提方法的有效性。此外，在实验的运行时间上，本文所提CP-FCLR方法相对于传统方法有着较大的提升，从而可以证明此方法具有更好的实用性。

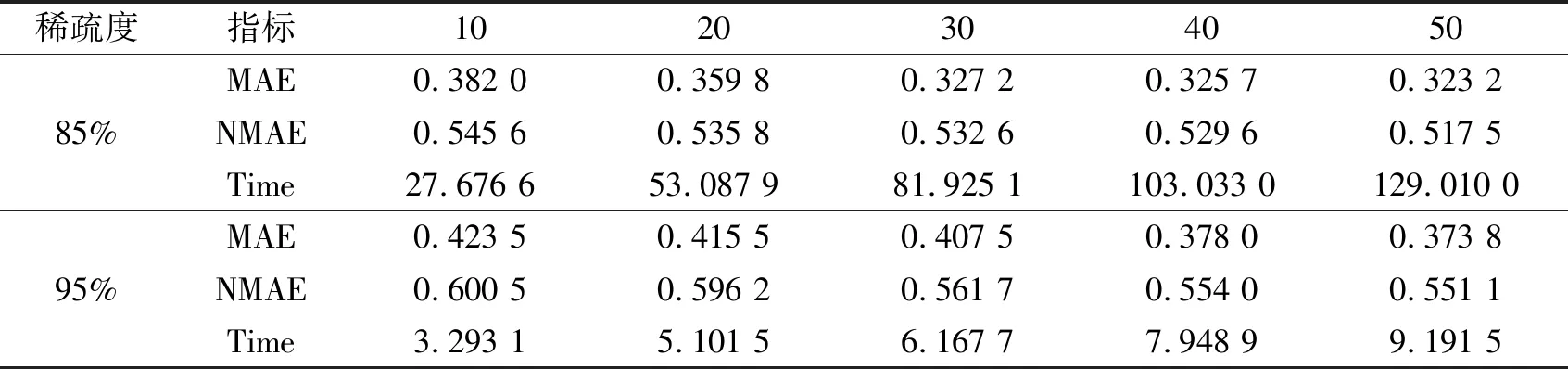
表6 在不同稀疏度与样本数量下的MAE、NMAE、Time

2.3.5 不同稀疏度下各种方法的对比实验

将本文所提方法在稀疏度为80%、85%、90%、95%的数据集上进行多次实验并取均值，将实验结果与UPCC、IPCC、WSRec、SVD、CACF、BBCF六种方法进行对比，具体见表7。

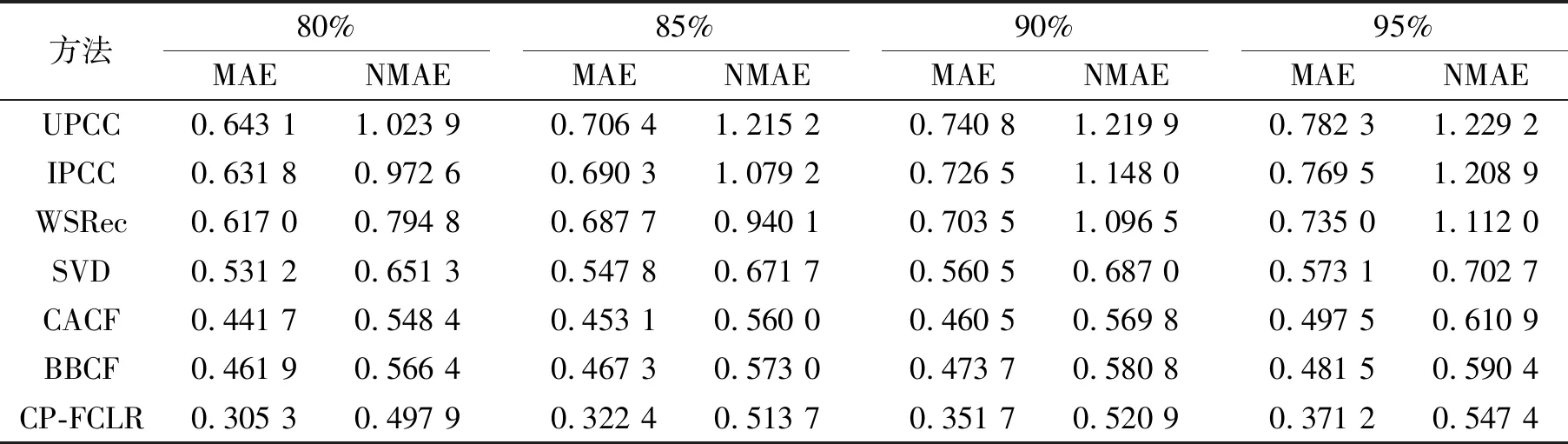
表7 不同方法在不同稀疏度下的MAE与NMAE对比

根据实验结果中评价指标MAE与NMAE的值进行对比可以看出，本文所提方法在QoS预测精度上相较于其他6种方法有着一定的提升。在不同稀疏度的情况下，本文方法相对于UPCC、IPCC、WSRec、SVD、CACF、BBCF六种方法所得实验结果的MAE分别平均降低了53%、52.1%、50.8%、39%、28.4%、27.2%；NMAE分别平均降低了55.5%、52.5%、46.5%、23.3%、10%、9.1%。同时，在数据稀疏度比较高的情况下本文所提CP-FCLR方法依旧有着更加良好的预测精度。

3 总结与展望

本文针对用户与服务的地理位置因素以及历史QoS数据稀疏所造成预测精度较低这一问题，提出了一种基于位置关系模糊聚类的混合协同预测方法，利用一种改进的相似度计算方法并融合用户或服务位置关系相似度，缓解了地理位置因素对QoS预测的影响，同时在数据稀疏的情况下有着更优的预测精度。在之后的工作中，将会把位置关系上的模糊聚类与随机森林相结合，将隶属度作为特征进行随机森林分类，从而达到过滤噪声的效果。