不同质量流下轴流压气机叶片的疲劳特性研究

陆正午， 王军利， 李庆庆， 冯钰茹， 李金洋， 刘志远

(陕西理工大学 机械工程学院， 陕西 汉中 723000)

轴流压气机具有效率高、流量大、维护方便等特点，广泛应用于高炉鼓风、催化裂化、气体压缩等装置的供风设备。叶片是轴流压气机核心零件之一，主要承受离心载荷和气动载荷[1]。目前对于轴流压气机叶片疲劳寿命的研究方面，Li Qu-bo等[2]针对8B和8C两种复合材料叶片进行了动态状态和疲劳分析，与忽略气动力的传统方法相比，8B和8C的安全疲劳寿命分别降低了约32%和40%，证明了考虑气动力对疲劳寿命影响是很有必要的。Pan Xu等[3]对叶片进行流固耦合仿真，研究表明叶片根部是容易疲劳断裂的危险位置，并且叶片尖端的振动非常明显。Luo Shuai等[4]研究了失速和喘振对轴流压气机一级转子叶片疲劳破坏机理的影响，拉扭疲劳是由喘振引起的周期性拉扭应力引起的，而弯曲疲劳载荷是由旋转失速引起的。高庆[5]对叶片进行了寿命综合评估，结果表明叶片的低循环疲劳寿命往往有足够的储备，而高循环疲劳寿命在叶片的寿命研究中占重要地位。丁闯[6]采用流固耦合的方法，研究了不同载荷对叶片应力和模态的的影响规律及机理，发现离心应力占总应力80%以上，热应力占20%，气动应力占4%以下。付曦等[7]对叶片在典型工况下的离心载荷与气动载荷的作用造成的应力分布和疲劳损伤进行了分析，结果表明多级加载损伤曲线则可较为准确地描述叶片损伤演化过程的非线性损伤，与叶片实际损伤行为更为相符。

上述轴流压气机叶片的疲劳分析中，还未针对在不同质量流下轴流压气机叶片疲劳寿命的情况进行研究，而轴流压气机叶片在非设计工况下容易发生疲劳损坏[8]，因此，研究不同质量流下轴流压气机叶片的疲劳寿命分析是有需要的。本研究基于有限体积法求解叶片流场与温度场，通过插值技术将压力场与温度场加载到叶片表面，以瞬态分析方法求得载荷谱，分析研究不同质量流下轴流压气机叶片的疲劳寿命规律。

1 计算方法

本研究采用单向热流固耦合求解方法，以N-S方程求解流场，求得压力场、温度场后，利用GCI(globally conservative interpolation)插值技术将压力场、温度场加载到叶片的结构网格节点上，之后瞬态求解叶片结构平衡方程，得到叶片的位移场，求得应力分布及载荷谱，进而采用Gerber模型修正平均应力以Vonmises等效应力计算疲劳寿命。具体流程如图1所示。

图1 流程图

1.1 流体求解技术

由于轴流压气机内部流场是一个三维非稳态流场，流场边界会伴随叶片的转动发生周期性变化，从而引起轴流压气机的流场参数在一定范围内产生波动。在轴流压气机流场达到热平衡时，将其内流场视为准瞬态，对其进行热流固耦合数值模拟。计算流体动力学的理论基础是质量守恒定律、动量守恒定律、能量守恒定律，其方程如下[9]：

(1)

(2)

(3)

式中ρ是流体密度，t是时间，v是速度矢量，u、v、w是速度矢量v在x、y、z方向上的分量，p是流体压力，τxx、τxy、τxz是因分子黏力作用而产生的作用在微元体表面上的黏性应力τ的分量，fx、fy、fz为作用在流体上的质量力，T为温度，k为流体的传热系数，cp为比热容，St为流体内热源及由黏性作用流体机械转化为热能的部分，有时简称St为黏性耗散项。

1.2 结构求解技术

热流固耦合计算过程中，结构温度场和热弹性求解的有限元方程[10]为

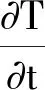
(4)

DU=GT+F，

(5)

式中M为热容量矩阵[10]，T为温度向量，t为时间，K为导热矩阵[10]，Q为热流向量，D为刚度矩阵，U为位移向量，G为热应力系数矩阵[10]，F为机械力向量。

热流固耦合界面上的流体与固体的位移、应力、热流量、温度等相等，满足下列公式：

rf=rs，n·τf=n·τs，qf=qs，Tf=Ts，

(6)

式中f为流体，s为固体，r为位移，τ为应力，q为热流量，T为温度。

在单向热流固耦合计算模型中，热传导方程的温度分布T受传递热量Q影响，本研究对轴流进行瞬态热分析，因流场求解得出的为稳态温度场，与时间t无关，故温度场式(4)中的温度向量T对时间t偏导项为0，采用有限元单元对方程机械离散，从而获得温度场的单元方程，求解瞬态时刻的温度场，接着将温度场代入热弹性方程(5)中，得到瞬态分析的位移场，进一步求得应力分布。

1.3 疲劳寿命分析理论基础

轴流压气机叶片的循环应力低于材料(Ti-6Al-4V)屈服强度(825～895 MPa)，主要为弹性变形，故疲劳破坏属于高周疲劳[11]。采用准静态分析法公式对载荷谱线性映射[12]：

(7)

式中σij，e(t)为叠加后弹性应力谱，k为载荷序号，Pk(t)为输入载荷谱，σij，e，k为静态强度计算结果中的应力，Pk，fea为所定义的第k种静态载荷。

平均应力修正模型选择Gerber模型，Gerber模型对于韧性材料的拉伸平均应力提供很好的拟合，与轴流压气机叶片的载荷相符。Gerber模型为[13]

(8)

式中σar为等效对称应力幅，σa为应力幅，σb为强度极限，σm为平均应力。

应力组合方法选择Vonmises等效应力，总应力计算公式为[14]

(9)

式中σB是叶片总应力，σn是法向应力，τ是切应力。

2 网格划分和数值计算结果校验

2.1 网络划分

本文研究的轴流压气机叶片为NASA Rotor 37。该轴流压气机叶片的基本设计参数见表1，流场模型如图2所示。叶片流场网格划分采用单圆对称(Single Round Round Symmetric)拓扑结构，这种拓扑结构在前缘和后缘处是对称的，适用于本研究中叶片的前缘和后缘为圆弧形的单叶片几何形状，如图3(a)所示。叶片结构采用四面体单元划分网格，网络节点数1 016 021，单元数659 899，如图3(b)所示。

表1 NASA Rotor 37 基本设计参数

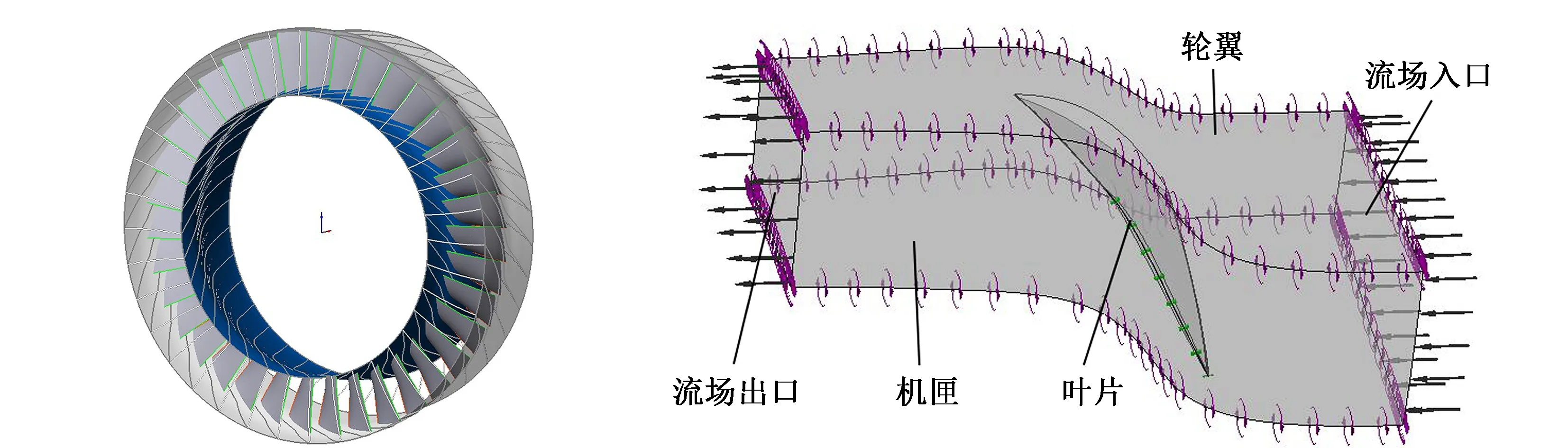
(a)Rotor 37示意图 (b)Rotor 37计算域内流场 图2 Rotor 37流场模型

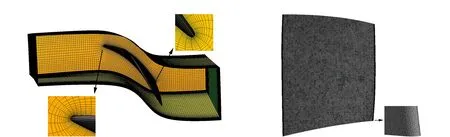
(a)流场 (b)叶片结构图3 模型网格划分

为了节省计算资源，分别选取37.6万、48.2万、58.87万、74.12万、120.64万、153.92万个节点数的网格进行流场网格无关性验证。图4为流场不同节点数的设计点性能参数计算结果，从图中可以看出，当节点数大于74.12万个时，总压比和绝热效率没有表现出明显的变化，压比相差0.44%，绝热效率相差0.05%。选取94.2万、95.6万、97.2万、101.6万、108.9万、117.8万、119.4万个节点数的网格进行结构场网格无关性验证。图5为结构场不同节点数的最大应力参数计算结果。因为瞬态求解的应力为周期性波动值，故选择最大应力全程平均值与第70个计算值已经稳定波动的波峰值判断结构场网格无关性。从图5可以看出，因为热流固耦合需要载荷插值传递，当网格数较小时，最大应力发生突增，当节点数大于101.6万个时，最大应力平均值和最大应力波峰没有表现出明显的变化，最大应力平均值相差0.21%，最大应力波峰0.208%。可以认为流场与结构场节点数到达了网格无关性的要求，为了减少计算时间，提高效率，故选择节点数为74.12万个网格划分来做叶片流场的数值计算，节点数为101.6万个网格划分来做叶片结构场的数值计算。

(a)总压比 (b)绝热效率图4 流场网格无关性验证

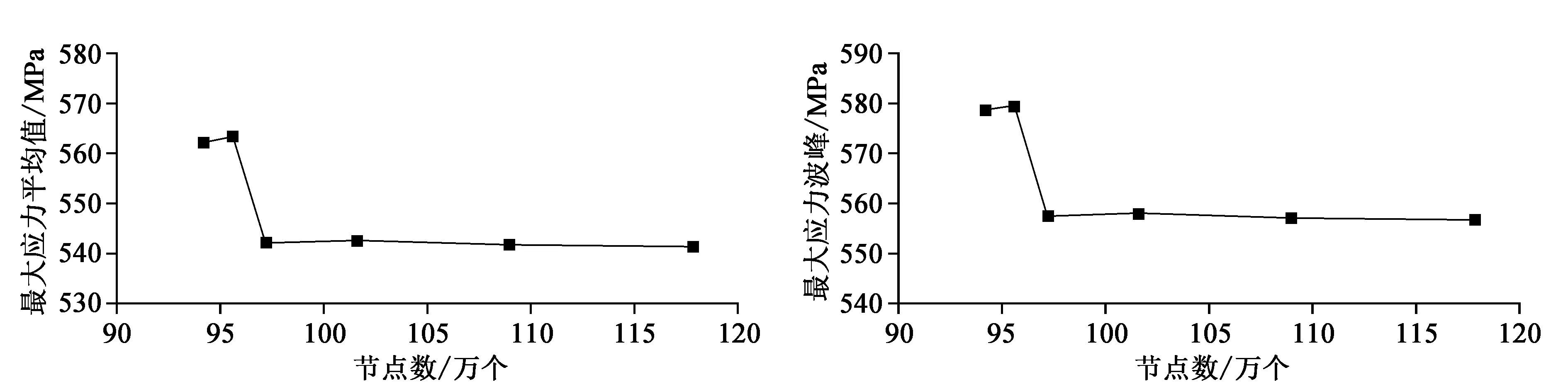
(a)最大应力平均值 (b)最大应力波峰图5 结构场网格无关性验证

2.2 数值计算结果校验

通过逐渐改变出口背压得到总压比与绝热效率特性曲线，以设计点为基准，通过持续减小背压到质量流近似不变时视为到达近堵塞状态，不断增大背压到流场求解，随着背压增大质量流减小，当质量流减小到一定值时总压比无法升高，视为近失速点，将其与实验结果比较，以验证数值计算结果。轴流压气机进口总温为288.15 K，进口总压101.325 kPa，出口设置为平均静压。采用在近壁区逆压梯度和分离流动有更好的预测精度的k-ωSST湍流模型[15]。图6为数值计算结果与实验结果[16]对比图，可见数值计算的总压比与绝热效率曲线与实验结果近似，求得近失速点质量流为19.434 kg/s，近堵塞点质量流为20.883 kg/s，数值计算结果与实验结果较吻合。以设计点质量流附近的工况20.19 kg/s作为代表，对比质量流为20.158 kg/s工况的数值计算结果与质量流为20.186 kg/s工况的实验结果，压比相差3.46%，绝热效率相差5%，数值计算的堵塞流量为20.883 kg/s，实验堵塞流量为20.93 kg/s，两者相差0.22%，验证了数值模拟结果的可靠性。

(a)总压比 (b)绝热效率图6 数值计算结果与实验结果对比

3 仿真结果分析

3.1 热流场求解结果

图7为近设计点叶片流场压力图。由图7(a)吸力面流场压力图可看出，压力由进口前缘减小后再增大，这是因为吸力面外凸，气流在前缘加速，故前缘压力减小，之后气流经过扩张，速度减小压力升高。由图7(b)压力面流场压力图可看出，压力在进口前缘最大，减小后再增大，这是因为压力面压缩气体且前缘半径很小，进口前缘压力最大，气流加速流动后压力减小，之后气流经过压力面内凹压缩气体，压力升高。

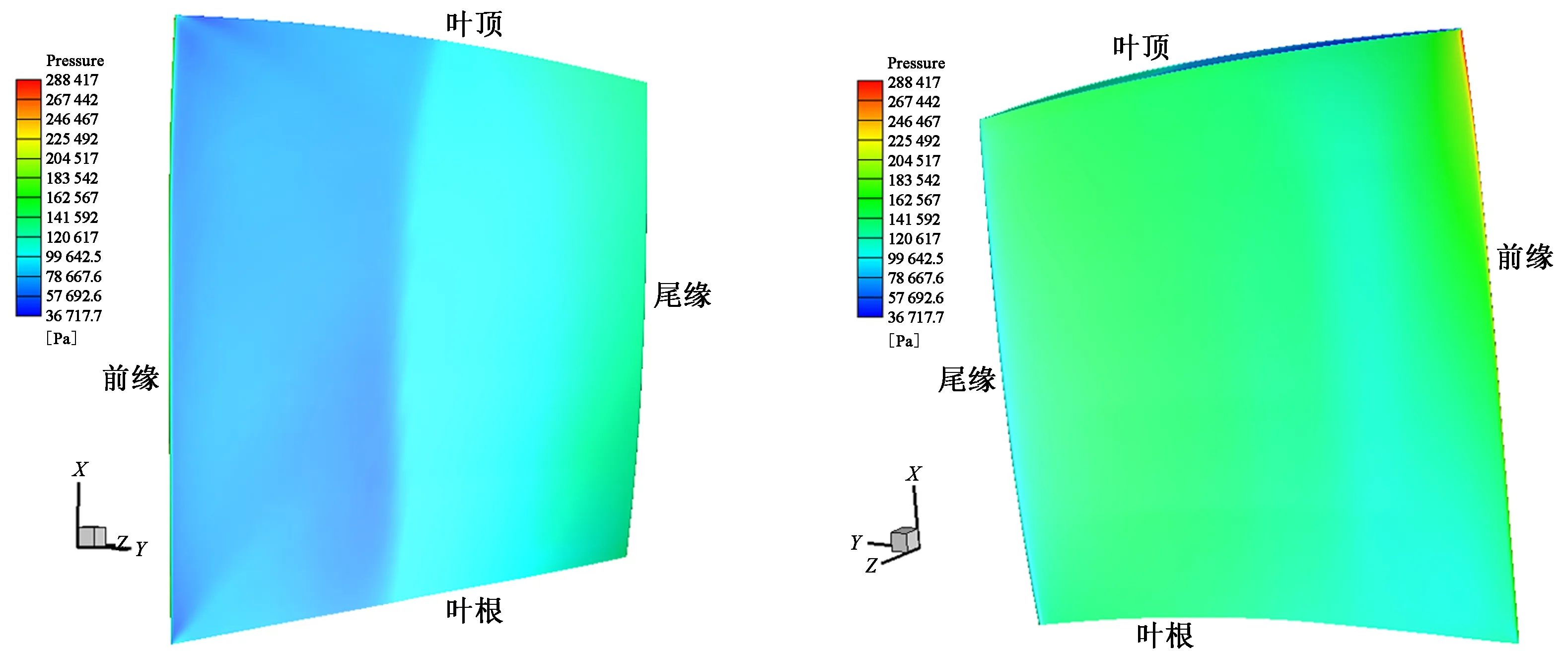
(a)吸力面 (b)压力面图7 近设计点叶片流场压力图

图8为近设计点叶片流场温度图。由8(a)吸力面温度图可看出，进口前缘的叶根处温度最低，中部到近尾缘处温度随叶片高度上升，这是由于间隙流由压力面加速后绕过叶顶到吸力面，与吸力面附面层作用，动能与势能化为热能，造成高温气体。由图8(b)的压力面温度图可看出，在叶顶中部到近尾缘处和进口前缘处温度较高。

(a)吸力面 (b)压力面图8 近设计点叶片流场温度图

图9为近设计点叶片流场极限流线图。由图9(a)吸力面流场极限流线图可看出，速度进前缘后有所降低，前缘到中部流动均匀，之后吸力面中部由于吸力面外凸与相邻叶片引发的槽道激波的共同作用在吸力面出现突降，吸力面中部到尾缘出现流动分离，再因为间隙流的影响，出现气流不稳定的现象，且在吸力面尾缘叶根出现涡流。由图9(b)压面流场极限流线图可看出，在经过前缘后出现略微加速，流动均匀，在叶顶由于间隙流的存在，气流不稳定，气流从压力面叶顶绕到吸力面，形成倒流与潜流。

选取99.9%叶高截面流线图、吸力面三维流线图，如图10所示。可以看前缘到中部间隙流从压力面绕过叶顶间隙后存在加速现象，且与吸力面附面层流体相互作用，动能与势能化为热能，造成相邻叶片压力面叶顶中部到近尾缘处和自身吸力面叶顶中部到近尾缘处存在高温区，与图8相对应。可以看到吸力面尾缘叶根出现涡流，且在吸力面中部至尾缘附面层存在由叶根向叶顶的流体，与图9相对应，这是由于附面层内气体微团的离心力远远大于主流区的气流微团产生离心惯性力，造成附面层内气体从叶根流向叶顶[17]。

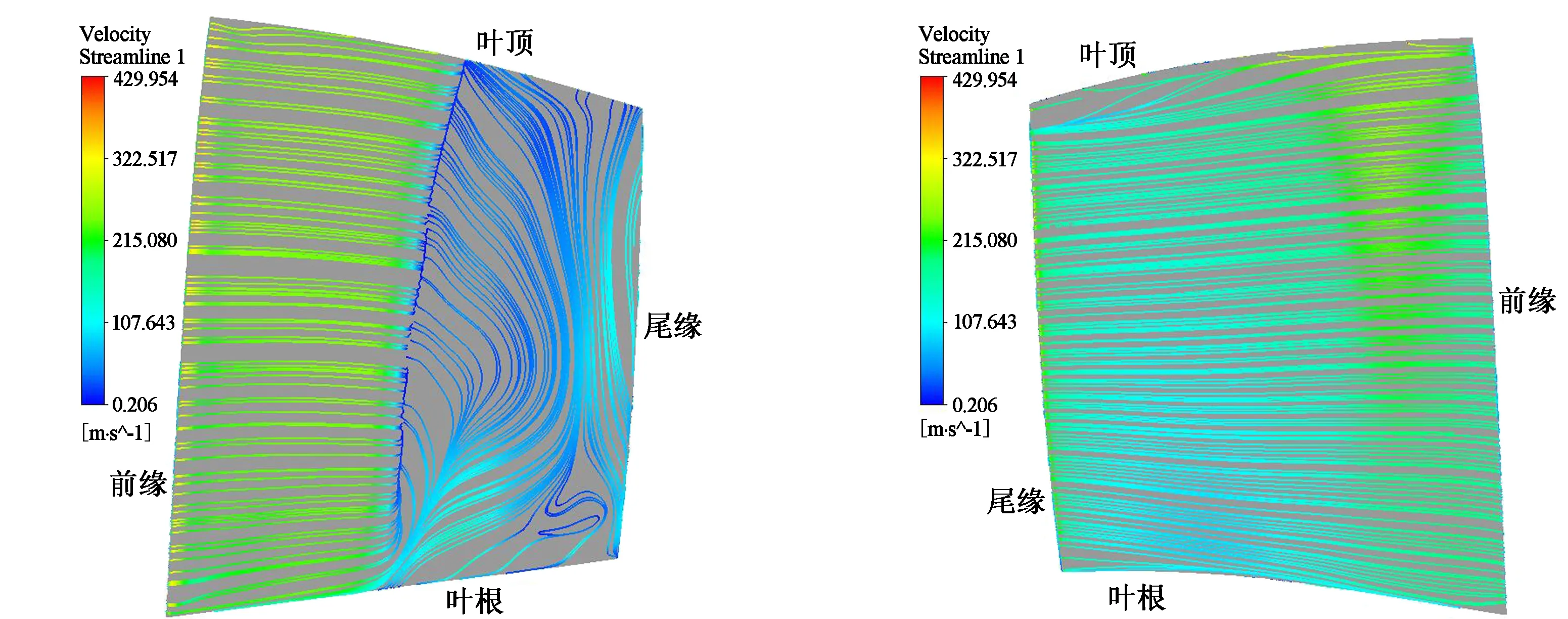
(a)吸力面 (b)压力面图9 近设计点叶片流场极限流线图

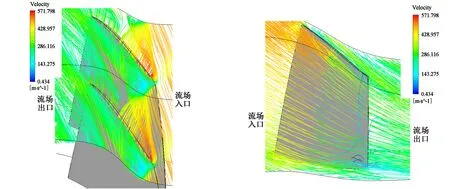
(a)99.9%叶高截面流线图 (b)吸力面三维流线图 图10 近设计点叶片流场三维流线图

图11为不同质量流下热流场对叶片压力分析图。由图11(a)最大压力对比图可看出，随着质量流增大最大压力减小，质量流达到20.566 kg/s后最大压力加快减小，达到20.847 kg/s附近开始堵塞后最大压力增加。由图11(b)最小压力对比图可看出，最小压力先略微减小然后增加后趋于稳定，达到20.847 kg/s开始堵塞后最小压力开始急剧增大。

(a)最大压力对比图 (b)最小压力对比图图11 不同质量流下热流场对叶片压力分析图

图12为不同质量流下热流场对叶片温度分析图。由图12(a)最高温度对比图可看出，随着质量流增大最高温度先减小，质量流达到20.489 kg/s后最高温度增加，达到20.761 kg/s开始减小，堵塞后最高温度近似不变约为386.23 K。由图12(b)最低温度对比图可看出，最低温度随着质量流增大而逐渐增大，堵塞后最低温度近似不变约为289.56 K。

(a)最高温度对比图 (b)最低温度对比图图12 不同质量流下热流场对叶片温度分析图

在近失速点质量流为19.434 kg/s时最大压力和最高温度最大，这是因为叶片压力面前缘存在因间隙流与激波作用产生的低能团比近设计点的更大；在近失速点时最小压力和最低温度较小，这是因为存在明显的前缘顶隙泄漏涡，间隙流能高速沿吸力面流动。

在近堵塞点时最大压力最小，这是因为叶片压力面前缘没有出现低能团，而是后移到相邻叶片吸力面；在近堵塞点时最小压力和最低温度最大，这是因为在近堵塞点吸力面没有产生明显的前缘顶隙泄漏涡，间隙流不能很好地流通。

3.2 瞬态求解结果

利用GCI插值技术将CFX求解得到稳态压力场、温度场结果加载到叶片的网格节点上，以时长0.015 s，初始载荷步50，最小载荷步45，最大载荷步100，瞬态求解叶片结构，得到应力分布及载荷谱。

轴流压气机叶片在出口背压为125 MPa下稳定工作后产生的压力场，其质量流为20.158 kg/s，而设计参数时质量流为20.19 kg/s，所以可将20.158 kg/s视为近设计点。瞬态求解得到近设计点叶片载荷图，如图13所示，最大应力逐渐趋于周期性，一个周期约为1.03×10-3s，最小应力趋于稳定在0.066 MPa附近，叶片的应力载荷具有周期性且低于材料(Ti-6Al-4V)屈服强度(825～895 MPa)，属于高周疲劳。

(a)最大应力对比图

(b)最小应力对比图 图13 近设计点叶片载荷分析图

截取1.027 9×10-2s到1.131×10-2s约一个周期的应力云图，图14为近设计点叶片压力面瞬态应力图，应力范围存在周期性缩小与扩大，最大应力变小时，应力范围变小，应力主要集中在进口前缘的叶根处，这是由于流体对叶片的力的方向主要是由前缘到后缘，加之指向叶顶的离心力的作用。图15为不同质量流下叶片瞬态求解最大应力平均值分析图，可看出瞬态求解最大应力平均值在质量流19.434 kg/s到20.158 kg/s有小幅的增大，在近设计点质量流20.158 kg/s之后加速减小。

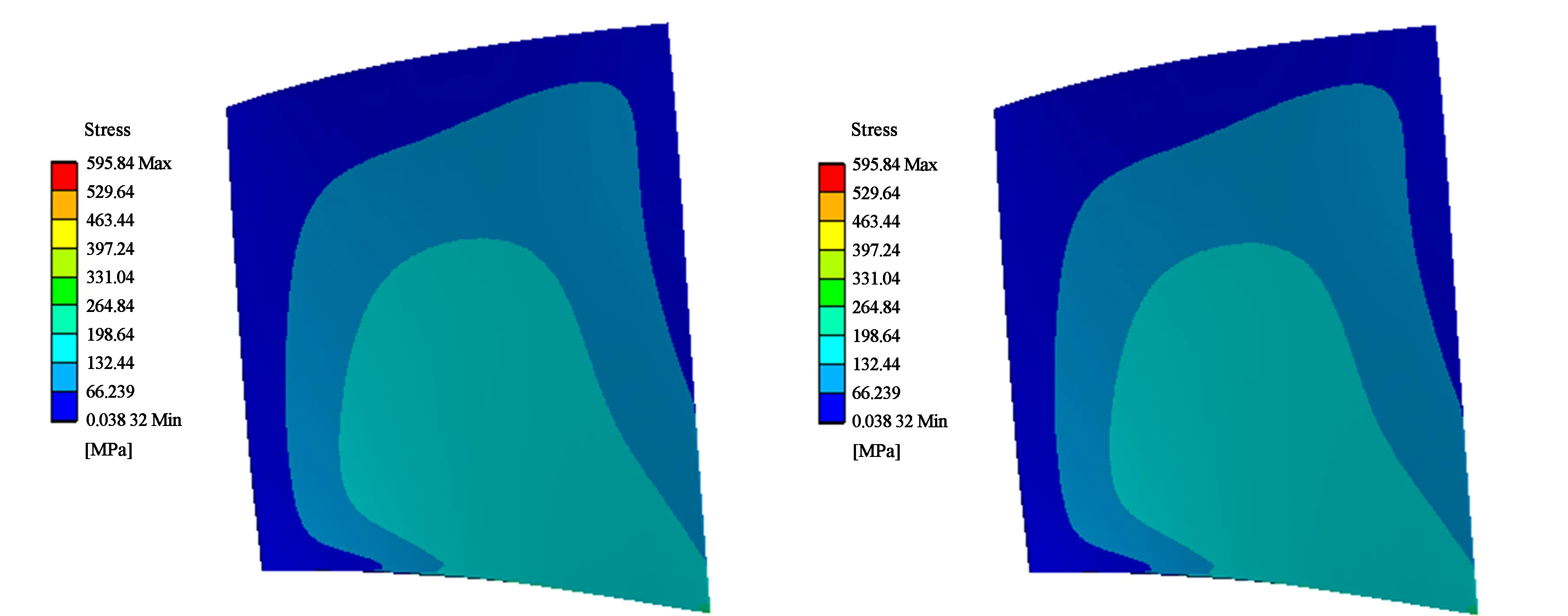
(a)t=1.027 9×10-2 s (b)t=1.045 1×10-2 s

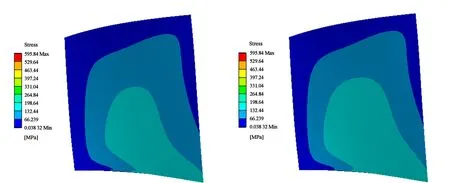
(c)t=1.079 4×10-2 s (d)t=1.113 9×10-2 s图14 近设计点叶片压力面瞬态应力图

图15 不同质量流下叶片瞬态求解最大应力平均值分析图

3.3 疲劳寿命求解结果

将瞬态求解得到的载荷谱采用准静态分析法对载荷谱线性映射到叶片的网格节点上，对载荷谱采用Gerber模型修正平均应力，以Vonmises等效应力计算疲劳寿命。图16为近设计点叶片疲劳寿命图，最低寿命循环为8.134×108周次，位于出口尾缘的叶根处，与文献[3]一致，如图16(c)所示，载荷谱每周次为0.015 s，计算得出最低寿命约为3389 h，与文献[18]中在最大连续工作状态工作3000 h可靠度在0.9以上相符合。

图17(a)为不同质量流下叶片疲劳寿命分析图，由图可知，质量流19.434 kg/s到19.740 kg/s，疲劳寿命略微减小，到近设计点质量流20.158 kg/s后开始加快增长，质量流20.761 kg/s到20.877 kg/s疲劳寿命大幅度增加，这是因为随着质量流的增加，应力在减小。图17(b)为不同质量流下叶片压比分析图，随着质量流增大，压比开始略微减小，到近设计点质量流20.158 kg/s后开始加快减小。

(a)吸力面 (b)压力面

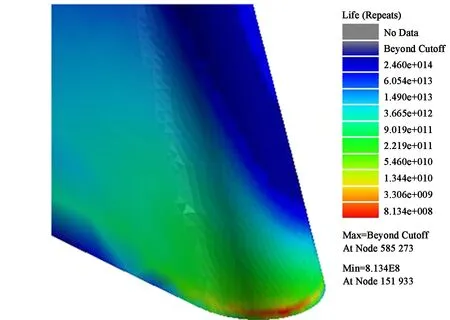
(c)疲劳危险部位图16 近设计点叶片疲劳寿命图

(a)不同质量流下叶片疲劳寿命分析图 (b)不同质量流下叶片压比分析图图17 不同质量流下叶片的疲劳特性

4 结论

本研究基于热流固耦合方法，模拟了不同质量流下轴流压气机叶片的工作情况，通过N-S方程求解流场，求得压力场、温度场后，加载到叶片的结构网格节点上，之后瞬态求解叶片结构平衡方程，得到叶片的位移场，求得应力分布及载荷谱，采用Gerber模型修正平均应力，以Vonmises等效应力计算疲劳寿命，得到以下结论：

(1)随着质量流增大，叶片热流场最大压力减小，达到堵塞后有所增加；叶片热流场最小压力随着质量流增大先略微减小后增加后趋于稳定，达到堵塞后最小压力急剧增大。叶片热流场最高温度随着质量流增大最高温度先降低，堵塞后最高温度近似不变；叶片热流场最低温度随着质量流增大而升高，堵塞后最低温度近似不变。

(2)热流固耦合瞬态求解的叶片最大应力逐渐趋于周期性，应力范围存在周期性缩小与扩大，应力主要集中在进口前缘的叶根处，且低于材料(Ti-6Al-4V)屈服强度(825～895 MPa)，叶片疲劳属于高周疲劳，而叶片最小应力趋于稳定；最大应力随着质量流增大先有小幅的增大随后加速减小。

(3)疲劳危险部位为出口尾缘的叶根处，疲劳寿命在质量流19.740 kg/s开始缓慢增大，到近设计点质量流20.158 kg/s后开始加快增长，质量流20.761 kg/s到20.877 kg/s疲劳寿命大幅度增加，而随着质量流增大，压比开始略微减小，到近设计点质量流20.158 kg/s后开始加快减小，故需要平衡疲劳寿命与压比。