双列圆锥滚子轴承滚道表面波纹度对轴承振动特性的影响研究

吕润楠， 郝 旭， 于长鑫， 矫文聪， 于泽洋

(瓦房店轴承集团国家轴承工程技术研究中心有限公司，辽宁 瓦房店 116300)

双列圆锥滚子轴承因其结构紧凑、摩擦力矩小、承载能力强而被广泛应用于铁路机车、汽车轮毂、机床主轴、飞机起落架等机械设备。滚动轴承在生产加工过程中，由于机床精度、夹具定位误差以及振动等因素的影响，使得滚道表面不可避免的存在波纹度等形状误差[1]。而轴承表面波纹度是影响其振动特性、噪声、疲劳寿命的主要因素，研究带有表面波纹度轴承系统的振动特性具有重要的意义。

在考虑表面波纹度的轴承系统研究中，Aktürk等[2]将钢球简化为无质量的非线性弹簧，研究了表面波纹度对球轴承振动特性的影响。Yhland[3]通过试验得出了波纹度波数对轴承轴向和径向振动频率的影响规律。Wardle等[4]研究了钢球数目和波纹度波数对轴承振动特性的影响。Harsha等[5]基于Lagrange方程研究了轴承-非平衡转子系统的非线性振动响应规律，并指出滚动体数目和波纹度波数是影响系统动力学特性的两个重要因素。邓四二等[6]利用能量守恒定律，研究了角接触球轴承零件工作表面的波纹度对轴承摩擦力矩波动性的影响。杜秋华等[7]在考虑弹流润滑的基础上建立了波纹度球轴承非线性振动模型，分析表明波纹度会使球轴承刚度发生周期性变化；充分润滑时，油膜会使轴承刚度略微增加。侯磊等[8]针对双转子-中介轴承系统建立了考虑中介轴承波纹度双转子系统模型，并讨论了波纹度幅值、波数等对转子系统振动特性的影响。邵建敏等[9]应用计算机求解了二自由度球轴承振动方程，分析了表面波纹度球轴承的振动特性，结果表明只有特定的波纹度波数才能引起系统特定频率的振动；滚动体波纹度较滚道波纹度对系统振动影响大。刘静等[10]以三自由度圆锥滚子轴承为研究对象，考虑润滑油膜影响，提出时变激励的挡边波纹度动力学模型，研究了波纹度对轴承振动响应特征的影响规律，并通过试验验证模型的有效性。顾晓辉等[11]利用分岔图、功率谱图和庞加莱截面图研究了轴承表面波纹度幅值和转速对系统的非线性振动的影响，并将关联维数应用于滚动轴承的故障诊断。张耀强等[12]对考虑轴承滚道表面波纹度的轴承-转子系统动进行了相关分析，发现当外圈波纹度波数与滚动体数目相等时，系统会产生强烈振动；内圈波纹度引起振动的峰值频率与波数有关。仿真分析方面，刘国云等[13]将滚子等效为力元，利用SIMPACK动力学软件建立了波纹度轴承动力学计算模型，并研究了波纹度幅值和波数对振动特性的影响。

现有的滚动轴承表面波纹度分析模型，多是基于Lagrange方程，提出不同自由度波纹度轴承系统的运动方程，并用Runge-Kutta数值算法对方程进行求解。然而该方法是将滚动体等效为弹簧，忽略了滚动体的质量，而轴承在实际运转过程中滚动体和套圈、保持架的接触碰撞十分复杂，从而难以准确模拟轴承实际运行状态。

本文在考虑弹流润滑以及时变接触刚度的基础上，应用ADAMS建立了双列圆锥滚子轴承波纹度动力学模型，分析了波纹度状态下双列圆锥滚子轴承的径向振动位移频谱和峰峰均值曲线，研究了波纹度波数和幅值对轴承振动的影响规律，为轴承的设计与制造提供了指导意义。

1 波纹度轴承建模

当滚动轴承表面存在波纹度时，滚动轴承表面由光滑曲面变为波纹曲面。假定轴承波纹曲面为正弦波形，在图1所示的波纹度示意图中，波纹度A可以表示为

A=Ansin(Nwθnj+β),j=1,2,…,Z

(1)

式中：n=i，o分别为内、外套圈的角标，下同；An为波纹度幅值；Nw为波纹度阶次，即波数；θnj为第j个滚动体与滚道接触点的角位置；β为初始相位角。若轴承外圈固定，内圈旋转，则有

(2)

式中：Z为滚动体数目；ωc和ωi分别为保持架和内圈角速度，且有

(3)

式中，Ri和Ro分别为内、外套圈滚道半径。

本文采用的双列圆锥滚子轴承型号为353132B，主要结构参数如表1所示。为能准确描述轴承在运转过程中滚子和套圈滚道及挡边不同的接触状态，在建模时将波纹度内圈滚道和大挡边分别建模，装配后的模型如图2所示。

2 动力学模型建立

轴承内、外套圈和滚子材料均为GCr15轴承钢，保持架材料为玻璃纤维材料，材料参数如表2所示。计算所用的润滑油主要参数如表3所示。

表2 材料参数Tab.2 Material parameters

表3 润滑油主要参数Tab.3 Main parameters of lubricating oil

2.1 impact函数

滚子和内外圈、保持架之间采用冲击函数法即impact函数来计算接触碰撞力，impact函数的一般表达式为

(4)

式中：x为两碰撞物体的实际距离；x1为触发距离； dx/dt为两物体间距离随时间的变化率，即速度；Kζ为接触刚度系数；e为弹性力指数，点接触取1.5，线接触取10/9；Cmax为阻尼系数最大值，取10 N·s/mm；d为切入深度，取0.1 mm。

2.2 接触刚度系数计算

工程应用中常用的Palmgren线接触弹性变形公式与弹性体曲率半径无关，从而无法描述滚道表面波纹度对接触面曲率的影响。丁长安等[14]基于一般弹性体接触理论，给出了线接触弹性变形δ的计算方法，即

(5)

式中：E为等效弹性模量，由两接触物体材料的泊松比和弹性模量共同决定；l为线接触有效长度；Q为接触载荷；Σρ为曲率和函数，曲率面的选取和曲率和函数的表达式仍参照丁长安等的研究。当套圈滚道表面存在波纹度时，Σρ不再为定值，此时求解上式即可得到滚子和波纹度套圈滚道间的接触刚度系数Kn。根据文献[15]中给出的计算方法，滚子大端面和大挡边间的点接触刚度系数可由式(6)给出

(6)

式中：k为椭圆曲率；Γ和Σ分别为第一类和第二类全椭圆积分。

Dowson等[16]提出的等温条件下弹流润滑接触最小油膜厚度hmin的计算公式为

(7)

式中：U=η0u；ε为黏度的压力指数；η0为常压下动力黏度；u为接触表面平均速度；R为当量曲率半径；q为单位接触长度上的负荷。

进一步，油膜刚度系数Kφ可表达为

(8)

综合上述推导，弹流润滑条件下滚子与挡边间的等效接触刚度系数Kdψ、滚子与波纹度套圈滚道间的等效接触刚度系数Knψ的表达式为

(9)

受套圈滚道表面波纹度的影响，滚子和滚道接触表面的曲率不再为定值，油膜刚度系数Kφ、线接触刚度系数Kn和等效接触刚度系数Knψ均是时变的。为能准确描述滚子和波纹度套圈滚道间的接触刚度系数，采用ADAMS提供的位置函数[17-18]来定义时刻变化的等效接触刚度系数Knψ，并将其值赋给impact函数中的接触刚度系数Kζ。

2.3 边界条件

为模拟轴承运行过程中内圈旋转、外圈“固定”的实际工况，将内圈滚道与挡边间添加固定副，将内圈与大地间添加转动副。为“固定”外圈，但不至于使其失去振动，将外圈与大地间添加扭簧，设定转动刚度系数和转动阻尼系数分别为为1×1010N·mm·deg-1和1×108N·mm·s·deg-1，转速通过转动副内置函数[19]添加。

轴承载荷边界为：径向力100 kN，轴向力50 kN，内圈和隔圈转速900 r/min，重力方向竖直向下。设定仿真时间1 s，初始积分步长0.001。

3 模型验证

当轴承内外圈转速一定时，保持架理论转速为

(10)

式中：nc和ni和分别为保持架和内圈转速；no为外圈转速；Dpw为滚子节圆组直径；α为接触角； 计算得nc=390 r/min。

仿真环境下得到的无波纹度轴承保持架转速，如图3所示。由图3可知，仿真环境下保持架转速RMS值为2 341.85 deg/s，即390.31 r/min，与理论转速误差仅为0.08%。该误差处于合理范围，同时也验证了本研究在动力学方面的合理性。

4 结果分析

由轴承几何参数和内圈转速计算可得：圆锥滚子轴承轴转频fs为15 Hz，保持架转频fc为6.5 Hz，单个滚动体在内圈滚道的通过频率fi为8.5 Hz。

4.1 内圈波纹度对轴承振动的影响

为研究内圈波纹度波数对轴承振动的影响，设定内圈波纹度幅值Ai为4 μm，初始相位角β为0，内圈波纹度波数Nw分别为18、20、21、22、23、34、32、40、42、43、44、45，不同内圈波纹度波数下圆锥滚子轴承径向振动位移频谱，如图4所示。由图4可知，在选取的九种波数下，轴承径向振动位移响应的频谱中均出现Zfc及其倍频，这与滚子通过外滚道频率的理论值接近；当Nw=λZ时，轴承径向振动位移响应的频谱图出现pZfi(λ,p均为正整数)及其倍频成分；当Nw≠λZ时，轴承径向振动位移响应的频谱图出现pZfi±qfs(q为正整数)及其倍频成分。此外，当Nw=λZ时，轴承径向振动位移响应的频谱图在频率λZfi处取得峰值，此时轴承振动水平较高。表4给出不同内圈波纹度波数时，轴承径向振动位移响应的频谱图峰值处对应的频率。结合表4和图4可得：若波数Nw和滚子个数Z满足关系Nw=κZ+τ(κ为非负整数，τ为整数，且-11≤τ<11)，则振动位移频谱图峰值点对应频率ff可由式(11)给出

表4 不同内圈波数下的峰值频率Tab.4 Frequencies of peak values with inner race of various wave numbers

(11)

当滚动体每次通过内圈波纹度波峰时，系统也会产生一次振动，这即为波通过振动WPV(wave passage vibration)，波通过振动频率fwpv可表达为

fwpv=Z(fs-fc)

(12)

于是，式(11)可改写为

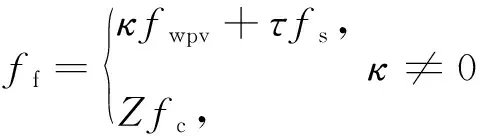
(13)

式(13)所示位移频谱图峰值点频率和波数间的数学关系与张耀强等给出的内圈波纹度轴承振动规律基本一致，即当内圈波纹度波数接近滚动体个数或其整数倍时，系统会产生特定的峰值频率。

4.2 外圈波纹度对轴承振动的影响

为研究外圈波纹度波数对轴承振动的影响，设定外圈波纹度幅值Ao为4 μm，初始相位角β为0，外圈波纹度波数Nw分别为18、21、22、23、34、32、43、44、45，不同外圈波纹度波数下圆锥滚子轴承径向振动位移频谱，如图5所示。由图5可知，当外圈滚道表面存在波纹度时，轴承振动位移频谱的基频及倍频成分和峰值点频率主要为Zfc及其倍频，该振动规律与刘国云等的研究基本一致；当外圈波纹度波数为滚子数目整数倍时，轴承径向振动位移响应的频谱取得峰值。

4.3 波纹度幅值对轴承振动影响

为研究滚道波纹度幅值对圆锥滚子轴承振动的影响，设定圆锥滚子轴承滚道波纹度波数Nw为22，套圈波纹度幅值An分别为2 μm，4 μm，6 μm，8 μm，10 μm，不同套圈波纹度幅值下轴承径向振动位移的峰峰均值如图6所示(峰峰均值：等间隔步长峰峰值的平均值)。由图6可知，当圆锥滚子轴承表面波纹度波数一定时，轴承在径向方向振动位移响应的峰峰均值随波纹度幅值的增大而增大，轴承振动越来越剧烈；相比于内圈波纹度，外圈波纹度对轴承振动影响较大。因此，在生产实际中，应合理控制套圈滚道波纹度波数并降低滚道波纹度幅值以减弱轴承在运转过程中的振动与噪声水平。

5 结 论

本文在考虑弹流润滑理论以及时变接触刚度的基础上，提出一种利用位置函数代替时变刚度系数的计算方法，建立了双列圆锥滚子轴承滚道波纹度动力学计算模型。通过分析轴承径向振动位移响应的频谱图和峰峰均值曲线可得如下结论：

(1) 滚道波纹度波数与滚子个数相等或是其整数倍时，振动位移频谱取得峰值，此时轴承发生强烈振动。

(2) 当内圈滚道存在波纹度时，振动位移频谱出现Zfc及其倍频、单个滚子通过内滚道频率和轴转频的组合频率成分(pZfi±qfs)，且峰值点频率与波纹度波数有关。当外圈滚道存在波纹度时，振动频谱峰值点频率为Zfc及其倍频。

(3)振动位移的峰峰均值随套圈滚道波纹度幅值的增大而增大；波纹度幅值一定时，外圈滚道波纹度对轴承振动影响较大。因此，为提高轴承工作性能并减小轴承在运转过程中的振动与噪声，在生产加工时应合理控制滚道波纹度波数并降低滚道波纹度幅值。