2022年加拿大奥林匹克试题例谈
2022-10-26单墫
高中数学教与学 2022年17期
单 墫
(江苏省南京师范大学数学科学学院,210023)
例1如图1,锐角三角形ABC内接于圆Γ,过点A作BC的垂线,交Γ于点D;过点B作AC的垂线,交Γ于点E.若AB=DE,证明:∠ACB=60°.
证明因为AD⊥BC,

例2用若干个下面的“丁四”(如图2)覆盖一个n×n的网格,恰好既不重合,也不溢出.问n应为什么样的值?
解显然4|n×n,所以n为偶数2k,而丁四为k2.

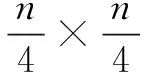
例3实数a,b满足
①
求
②
的值.
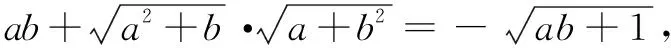
③
如何选择正负号?
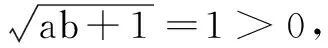
不妨设a>0>b,这时
=ab-ab=0>-1.
因此③ 式中应取“+”号,即
④
严格说来,还应指出④ 式可以成立(否则题目本身就不成立).
这里举一个例子,如
⑤
即可(⑤ 式使① 式成立).
