探析共同本源 拓展推广提升
2022-10-26马月朋
高中数学教与学 2022年17期
马月朋
(黑龙江省绥化市青冈县第一中学校,151600)
以高考为导向的教学理念,是以高考题考查的内容为教学主体,以高考题体现的数学思想为教学核心.这种理念得到了广大数学教师的赞同与推行,其根本原因在于高考题更准确地把握了数学核心素养及其本质.因此,对过往高考题进行纵向分析及串联,并从中探析若干高考题的共同本源,就显得尤为重要.
一、初探
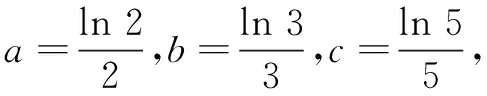
(A)a (C)c (2)(2017年全国高考题)设x,y,z为正数,且2x=3y=5z,则( ) (A)2x<3y<5z(B)5z<2x<3y (C)3y<5z<2x(D)3y<2x<5z 由此应用(1)的结论,可得3y<2x<5z.故选D. 据此,我们以例1(2)为例进行推广. 推广1设x,y,z为正数,且5x=py=qz(5 解由条件得 (1)当a=2时,求f(x)的单调区间; (2)若曲线y=f(x)与直线y=1有且仅有两个交点,求a的取值范围. 解(1)略. 通过研读高考题,找到他们的共同的本源,我们的题源就丰富起来,进而可以根据不同的考查目标编写习题,进而来服务我们的教学. (A)a (C)c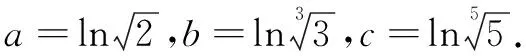
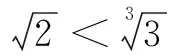
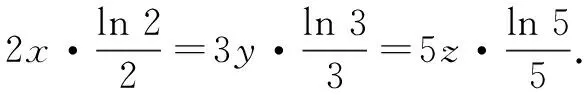
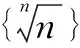
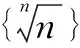
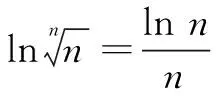
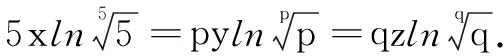
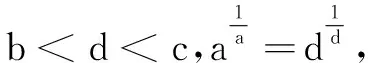
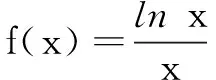
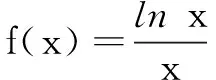
二、再探
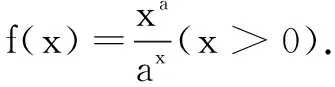
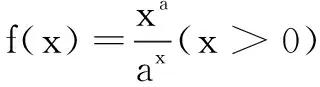
三、编题
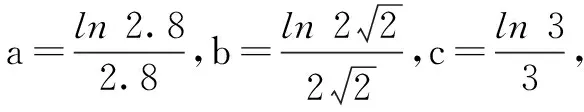
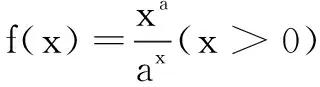
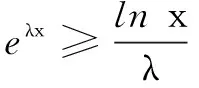
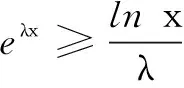
四、结束语

