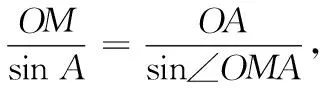高一数学测试
2022-10-26
一、单项选择题(本大题共8小题,每小题5分,计40分)
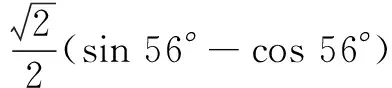
(A) sin 10° (B) sin 11°
(C)sin 12° (D) sin 13°
2.i为虚数单位,复数z满足z(2-i)=i2 022,则z=( )
3.函数f(x)=log2x+3x-4的零点所在的一个区间是( )
(A)(-2,-1) (B)(-1,0)
(C)(0,1) (D)(1,2)
4.已知正三角形ABC的边长为2,那么∆ABC的直观图∆A′B′C′的面积为( )
5.下列说法正确的是( )
(A) 1,2,3,4,5,6,7,8,9,10的第60百分位数是6
(B) 若甲组数据的方差为5,乙组数据为5,6,9,10,5,这两组数据中较稳定的是乙
(C) 数据1,2,3,3,4,5的众数为3、中位数为3.5
(D) 若x1,x2,…,x10的标准差为2,则3x1+1,3x2+1,…,3x10+1的方差是12
(A) 三边均不相等的三角形
(B) 直角三角形
(C) 等腰非等边三角形
(D) 等边三角形
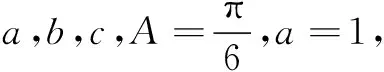
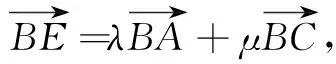
二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.下列命题中正确的是( )
(A) 已知a,b均为非零向量,若a∥b,则存在唯一的实数λ,使得a=λb
(B) 已知c≠0,且a·c=b·c,则a=b
(C) 两个非零向量a,b,若|a-b|=|a|+|b|,则a与b共线且反向
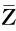
(C) 若z2为纯虚数,则a=b≠0
(D) 若|z-i|=1,则|z|的最大值为2
11.先后两次掷一枚质地均匀的骰子,A表示事件“两次掷出的点数之和是5”,B表示事件“第二次掷出的点数是偶数”,C表示事件“第一次掷出的点数是5”,D表示事件“至少出现一个奇数点”,则( )
(A)A与C互斥
(C)B与D对立
(D)A与B相互独立
12.如图,在三棱锥P-ABC中,PB⊥面ABC,∆ABC是直角三角形,∠B=90°,AB=BC=2,∠PAB=45°,点M,D,E,F分别为PB,AC,AB,BC的中点,则下列命题一定正确的是( )
(A)平面EFM∥平面PAC
(B)EF⊥PD
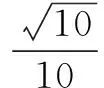
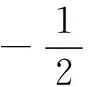
三、填空题(本大题共4小题,每小题5分,计20分)
13.设x,y∈R,向量a=(x,1),b=(2,y),c=(3,6),且a⊥c,b∥c,则向量a+b与a-c的夹角大小为______.
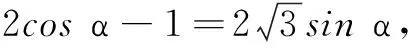
15.一艘轮船由海平面上A地向北偏西60°的方向行驶100海里到达B地,然后向C地行驶.设C地恰好在A地的南偏西60°方向上,并且A,C两地相距200海里,则轮船从B地到C地的距离为______海里.
16.已知三棱锥P-ABC的四个顶点都在球O的球面上,且球O的表面积为22π,AB⊥AC,PA⊥平面ABC,AB=PA=3,则三棱锥P-ABC的体积为______.
四、解答题(本大题共6小题,计70分.解答应写出文字说明、证明过程或演算步骤)
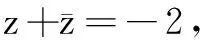

(1)求|a|;
(2)若向量c=3a-4b,d=ma+b,c∥d,求m的值.
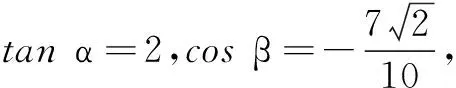
(1)求cos 2α的值;
(2)求2α-β的值.
20.(本小题满分12分)从学校的2 000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间,将统计结果按如下方式分成八组:第一组[65,75),第二组[75,85),…,第八组[135,145],如图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率;
(2)用样本数据估计该校的2 000名学生这次考试成绩的平均分;
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.
21.(本小题满分12分)如图所示的四棱锥P-ABCD的底面ABCD是一个等腰梯形,AD∥BC,且AD=2AB=2BC=4,PO是∆PAD的中线,点E是棱PD的中点.
(1)证明:CE∥平面PAB;
(2)若平面PAD⊥平面ABCD,且PA=PD,PO=AO,求点E到平面PAB的距离.
22.(本小题满分12分)如图所示,某市有一块空地∆OAB,其中OA=3 km,∠OAM=60°,∠AOB=90°.当地政府计划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖∆OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在∆OAM地带上形成假山,剩下的∆OBN地带开设儿童游乐场.为安全起见,需在∆OAN的周围安装防护网.设∠AOM=θ.
(2)为节省投入资金,人工湖∆OMN的面积要尽可能小,问如何设计施工方案,可使∆OMN的面积最小?最小面积是多少?
参考答案
一、单项选择题
1.B;2.A;3.D;4.D;5.B;
6.D;7.A;8.C
二、多项选择题
9.AC;10.ABD;11.ABD;12.ABC.
三、填空题

四、解答题
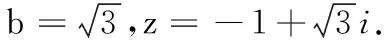
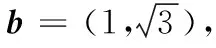
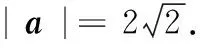
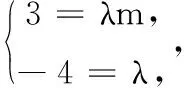
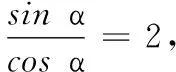
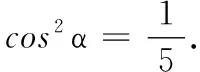
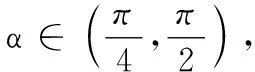
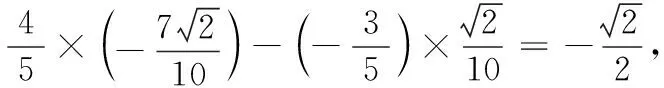
20.(1)由频率分布直方图,得第七组的频率为1-(0.004+0.012+0.016+0.030+0.020+0.006+0.004)×10=0.08.
(2)用样本数据估计该校的2 000名学生这次考试成绩,其平均分为70×0.004×10+80×0.012×10+90×0.016×10+100×0.030×10+110×0.020×10+120×0.006×10+130×0.008×10+140×0.004×10=102(分)
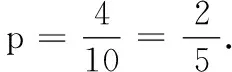
21.(1)如图,连结OC,OE.因为O,E分别是棱AD,PD的中点,所以OE∥PA.又PA⊂平面PAB,OE⊄平面PAB,所以OE∥平面PAB.
又AD∥BC,且AD=2AB=2BC=4,所以AO∥BC,且AO=BC.所以四边形ABCO是平行四边形,得CO∥AB.又AB⊂平面PAB,CO⊄平面PAB,从而CO∥平面PAB.
又CO∩OE=O,CO,OE⊂平面OCE,所以平面OCE∥平面PAB.又CE⊂平面OCE,所以CE∥平面PAB.
(2)由(1)知CE∥平面PAB,所以点E到平面PAB的距离等于点C到平面PAB的距离.连结AC,OB,因为O是棱AD的中点,且PA=PD,所以PO⊥AD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PO⊂平面PAD,所以PO⊥平面ABCD.
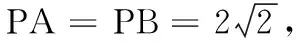
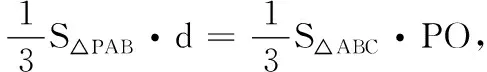
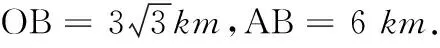
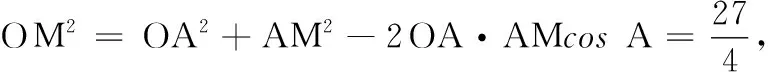
于是∠AON=∠AOM+∠MON=60°=∠A,∆OAN是等边三角形.故∆OAN的周长为3OA=9 km,即防护网的总长度为9 km.
(2)设∠AOM=θ(0°<θ<60°),则∠AON=θ+30°,∠OMA=120°-θ,∠ONA=90°-θ.