引发课题深度学习 发展学科核心素养*——以数列结构不良题的专题复习为例

谢建卿

(广东外语外贸大学实验中学，510540)

新时期高考改革的重要特征是从能力立意到素养导向,深度学习则是培养核心素养的重要途径之一.在高三的数学课堂上,由于时间紧、任务重,教师往往只注重基础知识、基础技能的积累、记忆和机械训练,学生只停留在浅层学习当中.一线教师应该在数学课堂上引导学生进行深度学习,让其“深”在其中,自然能习得素养.

结构不良题型是近几年高考命题的一种创新题型,相应问题具有一定的开放性,不同的选择可能会形成不同难度的问题,体现了数学教育素养导向的要求.鉴于平时学生不能准确地选出最优方案进行解题的现状,在高三专题复习中,以结构不良题型的问题解决教学为抓手,引导学生积极参与、主动建构,实现深度学习,落实和发展核心素养就显得十分必要.那么,教师该如何组织结构不良题型的教学,促使学生深度学习,提高课堂的有效性,落实数学核心素养的培养呢?本文以“数列结构不良题的专题复习”教学设计为例,结合深度学习理论,阐述如何落实数学核心素养的培养.

一、教学过程设计与教学片段

环节1课前准备 任务驱动

课前布置主题任务,让学生查阅历年的高考题,从2017年至2019年的全国高考I卷,从2020至2021年的全国新高考I卷,了解数列的考点和考查方向.

设计意图任务驱动下促进学生积极投入到高考题分析中,了解数列考查的内容和方向,明确专题复习的目标和要求,为有效备考作铺垫.

环节2问题引领 唤醒经验

例1(2015年天津高考题)已知{an}是各项均为正数的等比数列,{bn}是等差数列,且a1=b1=1,b2+b3=2a3,a5-3b2=7.

(1)求{an}和{bn}的通项公式;

(2)设cn=anbn,n∈N*,求数列{cn}的前n项和.

问题1数列{an},{bn}的基本量是什

么?它们由题设条件如何确定?

问题2选择哪种方法求等比数列{an}、等差数列{bn}的通项公式?

设计意图设计递进式问题串,引导学生主动思考,逐步解决问题.对求解高次方程有困难的部分学生,需结合换元思想的点拨促成解决问题.

问题3数列{cn}的通项公式cn=(2n-1)2n-1有何特点?如何求和?

追问2n+1与2n有什么关系?

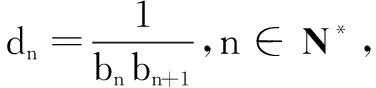
设计意图通过问题引领帮助学生梳理数列求和的常用方法,在错位求和遇到困难时借助追问促使学生深度思考、迎接挑战,在巧妙转换中体验成功.

环节3合作交流 深度学习

问题5从问题结构上看,变式1与例1有什么不同?

问题6变式1求解的关键是什么?

问题7求数列{an}的通项公式选哪一个方案才是最优?

设计意图对于条件部分缺失的结构不良题,由于问题初始状态不明确,增加了解题的难度,教师启发学生只要选一个条件放入题目中就成了结构良好题,采用转化的数学思想,把问题转化为熟悉的常规题来解.

为了促成深度学习的发生,教学采用合作学习的方式,分三步组织教学实施.

步骤1搭脚手架,助其独立思考

师:请在表1中选择一个条件进行解题,在所选条件后面打“√”

表1:变式1解题要点

设计意图基于学生对此类题型的解题经验不足,教师通过表格形式为学生搭建解决问题的脚手架,耐心等待学生独立思考并完成至少一种解法.笔者巡视发现大部分学生一般只选择其中一个方案进行解答.

步骤2任务驱动,学生因需讨论

笔者适时将学生进行分组,进行任务分配:各小组先选取一种方案进行深入探究,在完成解决目标的前提下继续完成其他方案的探索.

设计意图专题探究促使小组成员积极进行组内交流讨论,在任务的驱动下多角度去深入思考问题.教师设定限时讨论,小组成员之间分享自己的解法,课堂学习气氛再次高涨.笔者巡组发现每个小组讨论了至少两种方案的解法.

步骤3鼓励交流,展示成果

(各小组派一个学生代表上台展示)

师:(追问)分两种情况讨论,最后还需要做什么?

生1:哦,我忘记判断两种情况的结果是否能统一了.补充:当n=1时也满足an=n,综上得an=n(n∈N*).

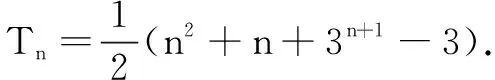
学生2走上讲台,非常自信地展示方案②.

师:基本量法是解决数列问题的通性通法, 请问还有其他解法吗?

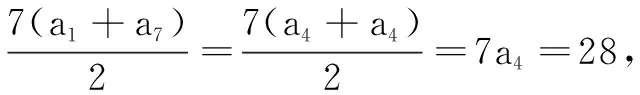
师:使用等差数列的性质进行计算很快捷!但最后得出an=n含合情推理,理论上需用基本量法逻辑论证.

师:(追问)因为2a2=a1+a3成立就能得出{an}是等差数列吗?

众生:要满足任意三项有2an=an-1+an+1成立,这个做法不对.

师:那方案③该怎么思考呢?

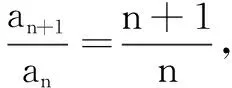
师:真棒!请问什么时候使用叠乘法呢?

师:通过本题解答,结构不良题该如何选择最优方案呢?

众生:观察所有方案,选择一种计算量少自己又擅长的方案.

设计意图解决结构不良题关键在于如何选择最优方案,通过师生、生生的合作交流与模式展示,帮助学生体验最优方案的选择过程及视角.这是一个有意义的学习过程,既能促进学生掌握相应核心知识、解题方法和步骤,又能形成积极的内在学习动机,提供学生内在思维外化表达的机会.

变式2在等差数列{an}中,已知a6=12,a18=36.

(1)求数列{an}的通项公式;

(2)若______,求数列{bn}的前n项和Sn.

师:请在表2中选择一个条件进行解题,在所选条件后面打“√”

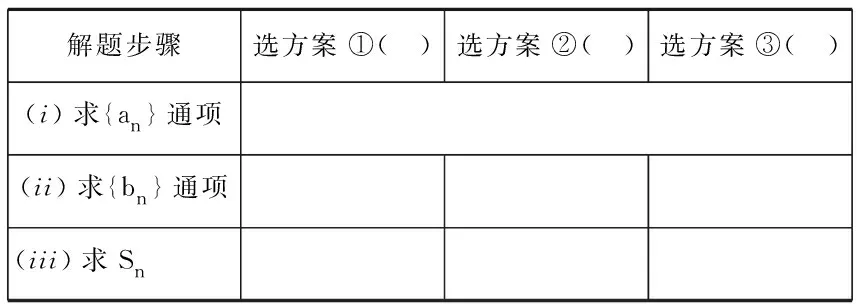
表2:变式2解题要点

设计意图尊重学生的认知规律,在学生的“最近发展区”设计恰当的教学材料变式2,成功吸引学生主动参与到教学活动中来,进行深度学习.变式2是求数列{bn}前n项和时出现结构不良题,不同方案的选择导致数列{bn}的求通项公式、求和的方法也不同.有了变式1的经验,学生能熟练使用基本量法求出an=2n.

问题8选择什么方案求数列{bn}的前项和Sn最好?

众生:选方案②.

老师邀请了举手的学生7.

师:裂项求和确实很简洁!谁愿意展示①和③?

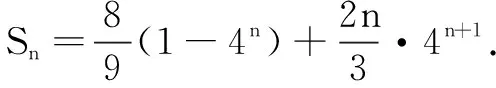
师:观察{bn}的通项特征,类比例1,用错位相减法也是可行的.

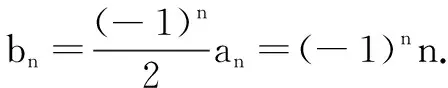
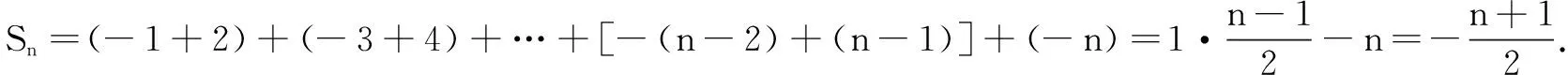
设计意图尊重学生的意愿,从方案② 开始展示,唯有“深”在人的心灵,才能吸引学生全身心投入.教师的适时提问,杜绝了学生偷懒不去思考方案① ③.因此以学生为主体的深度学习,让每一个学生都能得到不同的发展.

环节4迁移应用 新知内化

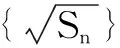
设计意图为了检验学生课堂学习效果,促使其学会知识的迁移和应用,实现新知内化.该题解法有3种组合方式:选① ② 作条件证明③;选② ③ 作条件证明①;其中选① ③ 作条件证明②.学生要对这三种组合方式作出选择.这需要学生在对基础知识很熟练的情况下快速判断.

二、促进深度学习的思考与行动

1.任务驱动,促使学生深度学习,发展核心素养落地

中国高考评价体系中的“四翼”要求高考命题体现创新性,设置新颖的试题呈现、设问方式[1].结构不良题型的出现为考生提供了独立思考、大胆创新的广阔空间,有利于学生摆脱思维定势的束缚,促进学科核心素养的发展.如变式1中方案① 的求解培养了学生分类讨论的思想和数学运算素养;方案② 的一题多解,培养了学生发散性思维和数据分析素养;方案③ 中叠乘法的运用有利于培养学生的数学抽象和逻辑推理素养.当然,教学过程中需要开展深度学习,实现相关知识的概念性理解．

2.探究学习,类比迁移知识,深度学习达成的重要途径

深度学习,更加强调较高层次的认知目标,强调高级思维能力的培养.本节课从典型考题引入,转入结构不良题的解答分析,再到一道高考真题课堂学习的效果的检测,启承转合,一气呵成,让学生在知识类比、迁移、应用的过程中,经历从良构到不良问题的解答,培养了学生观察、辨析、运用的综合思维能力,也提高学生分析、发现、解决问题的能力,感悟函数思想、化归与转化的思想,落实培养学生数学抽象、数学运算、逻辑推理等数学核心素养.

3.合作学习、交流展示成果是深度学习实现的有效学习方式

当儿童在没有教师的控制下与伙伴讨论时,更可以开发、延伸讨论与辩证,而这样的讨论使他们成为更主动、更独立的知识拥有者[4].在合作学习过程中,每一个人独立思考、小组同学的思考、整个班级对话的顺序开展,

增加了学生“内言外化”的机会,促进了学生主动积极地投入教学活动中去[3].让学生在合作交流中实现深度学习的基本步骤是:搭建脚手架,促使学生独立思考;任务驱动,促使学生因需而讨论;展示交流,促使其高阶思维的形成. 在教学过程中,教师应是“适时”出现的引领者.

深度学习是一种“真学”. 高三学生带着先前已经学习并内化的知识走进课堂,教师必须唤醒这些经验,通过当下学习的新知识改造这些经验,使得片面的经验变得全面,繁杂的变得优化,错误的经验得以纠正[2].本案例只是一次教学尝试,不同的问题教学结果可能是相似的,但过程一定是有其自身的特殊性,需要我们去探索、实践．