用极化恒等式秒解数量积问题*

朱亚旸

(湖南省衡阳市衡东县第一中学，421400)

极化恒等式在平面向量与三角形、四边形、圆、球体、圆锥曲线、多动点等知识融合的数量积求值问题中有着广泛的应用,是解决此类复杂运算问题的强大数学工具之一.

一、极化恒等式

二、妙用举例

1.融合三角形,化繁为简

(A)∠ABC=90° (B)∠BAC=90°

(C)AB=AC(D)AC=BC

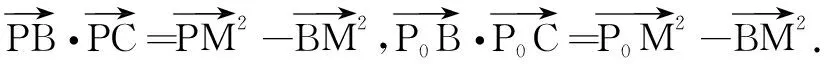
2.融合四边形,化难为易

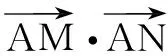
3.融合圆形,化曲为直

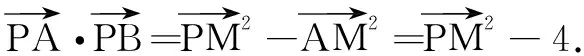
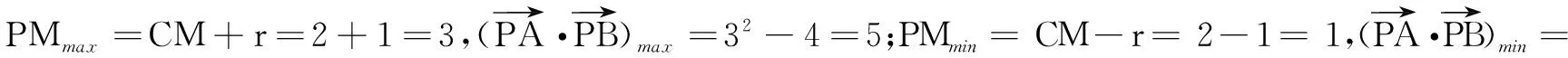
4.融合几何体,化体为面

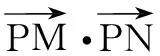
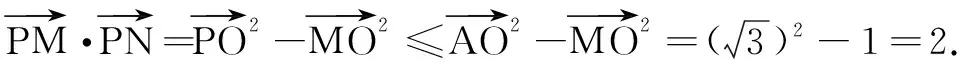
5.融合圆锥曲线,化动为静

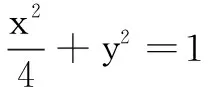
(C)5 (D)8

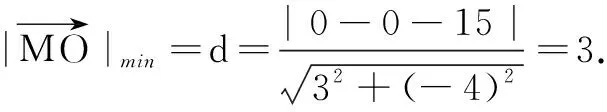
6.融合动点问题,化动为定

(A)0 (B)2 (C)3 (D)6

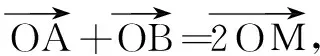
关于平面向量数量积的运算,从代数角度切入已深入人心, 而与几何图形结合的运算

则略显单薄.通过上述问题的求解,我们可以感受到极化恒等式的应用恰好弥补了这个缺憾,将平面向量数量积的运算借助几何图形表达展现得淋漓尽致,在解题过程中有广泛的应用前景.