把握问题本质 启发数学思考*——以微专题“一元二次方程在解析几何中的应用”教学为例

徐所扣

(江苏省扬州中学,225002)

《普通高中数学课程标准》(2017年版)指出:“高中数学课程以学生发展为本,落实立德树人根本任务,培育科学精神和创新意识,提升数学学科核心素养.”在发展学生数学核心素养的目标下,我们一线教师需要确立与之相适应的教学观:把握数学的本质,启发思考,改进教学.基于核心素养的数学课堂应立足于学生思维品质的养成,剖析问题的本质,启发学生进行数学思考.这是高中数学教学的关键.

运算是数学核心素养之一.对于圆锥曲线的相关计算问题,如果选择合适的解题方法,能够直达问题的本质,使计算的过程得以简化,故以圆锥曲线为知识载体评价学生的数学运算素养是高考常态.基于此,笔者在高三第二轮复习过程中开展了一次“一元二次方程在解析几何中的应用”微专题教学实践. 陈省身说:“数学是自己思考的产物,首先要能够思考起来,用自己的见解和别人的见解交换,才会有很好的效果.”现整理成文,与同仁分享.

一、教学实录

问题在平面直角坐标系xOy中,设二次函数f(x)=x2+2x+b(x∈R)的图象与两坐标轴有三个交点,经过这三个交点的圆记为C,则圆C是否过定点?

师:如何研究动圆过定点呢?

生1:先求出圆C的方程,圆C的方程含有参数b,再通过方程研究过定点问题.

师:说得对!求解本题的关键就是先求圆C的方程.那么如何求呢?

生2:设圆的一般式方程,设抛物线与坐标轴的三个交点的坐标,代入方程组解求出交点.感觉能做到,计算会比较繁一点,我还没算好.

师:确实如此,这是求圆的方程的基本解法——待定系数法.还有其他解法吗?

师:非常好,这位同学平面几何学得很好,他充分利用了圆的几何性质,直接得出了圆心的坐标,非常简洁(掌声).还有其他想法吗?

沉默…….

师:圆C经过点A,B,D,反过来换个说法,即A,B,D三点是抛物线、坐标轴、圆共同的交点,我们能否从这个角度去思考，促使问题解决呢?

生4:可以的.我对生1的解法进行了改进,还是设圆的一般式方程为x2+y2+Dx+Ey+F=0,令y=0,得x2+Dx+F=0,这与x2+2x+b=0是同解方程,故D=2,F=b;令x=0,得y2+Ey+b=0,此方程有一个根为b,代入得E=-b-1.所以圆C的方程为x2+y2+2x-(b+1)y+b=0,变形得x2+y2+2x-y-b(y-1)=0,从而圆C过两定点(0,1),(-2,1).

师:这位同学设出圆的一般式方程后,对系数的求解没有按常规强行计算,而是利用了一元二次方程同解的原理得出了系数的值,非常巧妙(掌声).这就是本节微课我们重点要研究的内容(板书课题——一元二次方程在解析几何中的应用).

1.利用一元二次方程的同解性,获得参数的值

(1)求椭圆C的标准方程;

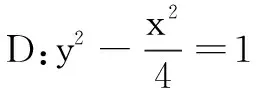
(i)证明:直线AB与圆x2+y2=1相切;

(ii)若直线AB与椭圆C相交于M,N两点,求∆OMN外接圆面积的最大值.

生5:一开始我也没有想到,用小猿搜题查了一下,看懂了之后然后再做的.

师:这位同学很诚实(笑声),不看解答确实不容易想到这样做,不过平时作业还是要养成独立思考的习惯.大家想想,能不能用今天讲的同解方程的方法来解决这个问题呢?

(1+2k2)x2+4kmx+2m2-3=0,

①

(1+k2)x2+(2km+D+Ek)x+m2+Em=0.

②

师:这位同学看出了问题的本质,即点M,N是直线AB与椭圆、圆的共同交点,从而尝试用同解方程来求解.由此可见,在平时的学习中要多总结、多思考,将学到的知识、方法在解题中灵活加以应用,古人云:“举一隅不以三隅反,则不复也.”

2.换元构造一元二次方程,关联韦达定理

(1)求C的方程;

(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.

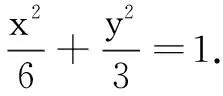
生7:由AM⊥AN,可得直线MN具有某种性质,这个性质我们通过直线MN的方程来研究:先考虑斜率不存在的情况;再考虑斜率存在时,设MN方程为y=kx+m,由AM⊥AN可得k与m的关系式.

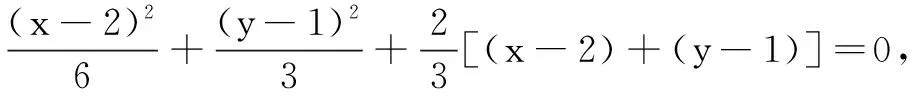
师:这种解法就是大家在教辅资料中常见的齐次化方法.这里我们由椭圆方程和直线方程,巧妙地构造了关于x-2和y-1的二次齐次式方程,相除换元后得到一个一元二次方程,而这个方程的两个根就是直线AM,AN的斜率;再利用韦达定理,得出m,n满足的关系式.

师:大家想一想,由以上解题的过程,我们还能发现什么结论?

生9:本题中k1k2=-1,其实k1k2=t(t为非零常数)时,都可得出直线MN过定点.

生10:我还发现,当k1+k2=t(t∈R)时,也可得出直线MN过定点.

二、课后反思

数学核心素养的培养很大程度上依赖于“用数学”的过程,数学核心素养的价值集中体现在“用数学”解决实际问题.“用数学”是在充分理解数学知识、数学思想方法的基础上用数学的眼光看问题,用数学的思维思考问题,用数学的语言表达自己的观点和研究成果.数学解题就是“用数学”的一种学习活动．本节课,作为微专题是通过两道题的师生交流,引领学生实现从联想一元二次方程到构造一元二次方程的思维进阶．在此过程中,例1利用了圆锥曲线的“截距”是一元二次方程的解,由方程的同解性直接得出参数的值.学生数学运算素养达成根据问题的特征形成合适的运算思路的一级水平．例2是将圆锥曲线方程变形为关于斜率分子、分母的二次齐次式,通过相除换元法构造一元二次方程,再通过关联韦达定理确定运算对象,学生的运算素养进阶到“提出运算问题,并借此探讨问题”的二级水平．

数学解题教学真正的价值在于将数学问题的逻辑通路从学生心理上产生,只有关注学生形成数学能力的心理过程,并仔细斟酌，做好相应得体的教学设计,教师才能有意识地将自己解决问题的方法变成促使学生素养形成的有效手段.当然,教学还要着眼于学生的最近发展区,为学生提供有挑战性的问题,调动学生的积极性,激发其潜能,从而达到超越其最近发展区而达到下一发展阶段的水平.

王尚志教授认为,培养并提升数学核心素养,不能依赖模仿、记忆,更需要理解、感悟,需要主动、自觉.虽然,思考数学问题、解决数学问题、提出数学问题都能发展学生数学学科核心素养,但培养学生提出问题的意识更为重要.