一道解析几何联考题的求解与溯源

石礼标

(江苏省清河中学,223001)

(1)求椭圆C的方程;

(2)若直线AD与直线BP交于点M,直线DP与x轴交于点N,求证:直线MN恒过某定点,并求出该定点.

这是今年3月份湖北八市联考第21题解析几何题,质量很高,解法也比较多.但从学生实际的解答情况看,第(2)问得分偏低,所提供的解法运算量也比较大.本文介绍第(2)问多种方法求解，并比较方法的优劣.

一、纲举目张 一动俱动

由于点P在椭圆上运动,导致M,N随之而动,因此设出点P,则点M,N立刻可求,进而得到直线MN的方程后寻求定点.

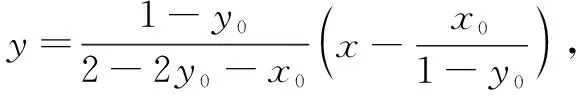
评注上面解法很容易理解,思路也比较自然,不足之处就是运算量较大,对学生的运算能力要求比较高.为了减少运算量,转换解决问题的视角.

二、整体代换 简化形式

设点法运算较繁的原因是用点的坐标写出斜率,其表达式自然不简捷,进而导致直线方程繁琐,无论是求两直线交点或直线与椭圆联立,运算量均不小.可考虑整体代换,直接设直线的斜率,进而表示出点M,N.

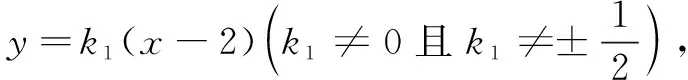
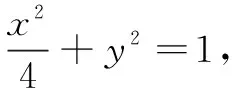
将点P的坐标代入y=k1(x-2),整理可得(1+2k2)(1-2k2)=-2k1(1+2k2)2,因为1+2k2≠0,所以1-2k2+2k1+4k1k2=0.

由点M,N的坐标,得直线MN的方程为

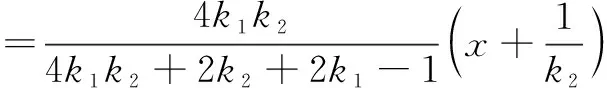
故直线MN过定点(2,1).

评注直接设斜率时运算量确实比解法1减少些,但依然没有改变运算过程形式复杂的本质.另外,解法2利用等式1-2k2+2k1+4k1k2=0合理替换直线MN方程的形式,对学生的思维与运算能力要求也比较高.

三、索本溯源 立足教材

上面两种方法运算量都不小,那就回到课本去!在中学课本中,从直线的点斜式y=k(x-x0)+y0,可知该直线必过定点(x0,y0).推广到一般情况,若直线l的方程为y=kx+b,且k,b满足一次关系式,则直线y=kx+b必过定点.

解法3设直线MN的方程为x=my+t,则点N(t,0)(t≠2).

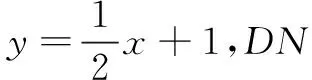
故直线MN方程为x=my+2-m,即x=m(y-1)+2,直线MN必过定点(2,1).

评注索本溯源意为是探索根源、寻找原因.要寻求方法的根源,必须从我们所学的知识入手.因此有关直线过定点问题应从课本关于动直线过定点的相关知识点出发,设直线方程为y=kx+b(斜率存在时),根据题设条件寻求k,b之间的关系求解.上面的解题过程显得自然,既符合学生的认知,且所设直线方程的形式简单,运算量也不会太大,这才是动直线过定点问题的返璞归真的解法!

上面三种解法优劣一目了然.再提供一种解法,让我们认清题目的本质.

四、化椭为圆 认清本质

将椭圆通过伸缩变换转化为圆,这样圆的相关性质就可以合理运用了.

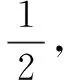
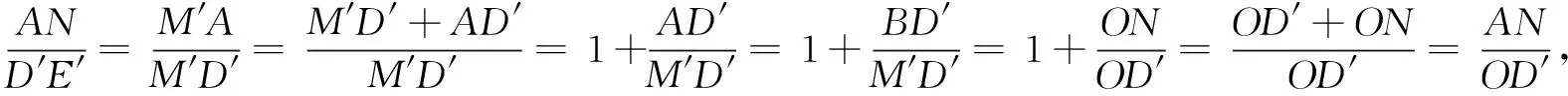
在解法4的基础上,我们很容易得到这类问题的如下本质属性.

解析几何题虽然入手方法较多,但一般运算量都比较大,学生得分普遍不高.平时学习中若能领会课本知识所蕴含的方法,并能熟练应用这些方法,才会以不变应万变,从课本最简单的相关知识处入手,用简约的思维解决复杂的问题.这种用最简单的、最直观的方法解决深刻的问题,才是数学之精髓,才是“返本归元”的真正含义.这就要求我们在数学解题教学中,不能满足题目如何解决,也要对题目的形成、求解方法进行系统地把握,在头脑中提炼一类问题的本质,力争做到题不在多,有法则行.通过一类问题的本质探究,对于核心方法的训练要在不同的环境中不断让学生体会到方法的重要性,以提高学生认清问题本质,对解题有更深的理解,便于发展学生的解题能力.