浅谈如何处理解析几何中的非对称式问题

彭晓琳

(湖北省宜昌市葛洲坝中学，443000)

在解析几何中,我们遇到的绝大部分题目都是运用韦达定理来解决,对韦达定理结构的对称式进行化简计算,学生是比较熟悉的.但在遇到非对称式问题时,大部分学生就很不适应,甚至无从下手.本文以一道高三调研试题为引例,谈谈非对称韦达定理问题常见的解法和思路,供参考.

一、试题呈现与解法探究

(1)求椭圆C的方程;

(2)设椭圆C的左、右顶点分别是A,B，点P,Q为椭圆上异于A,B的两动点,记直线AP的斜率为k1,直线QB的斜率为k2,已知k1=7k2,求证:直线PQ恒过x轴上一定点.

(2)思路1分设两线直接求解.

解法1由(1)知点A(-2,0),B(2,0),设点P(x1,y1),Q(x2,y2),直线AP的方程为x=t1y-2,直线BQ的方程为x=t2y+2.

评注此法为了回避出现非对称结构,不直接设直线PQ的方程,而是先通过设直线AP的方程与椭圆方程联立求出点P的纵坐标,同理得到点Q的纵坐标,再利用k1=7k2和P,D,Q三点共线这两个条件得到点D的坐标.思路清晰,学生容易接受,但计算量偏大.

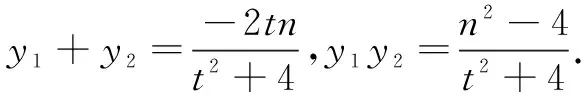
思路2韦达定理代入消元法

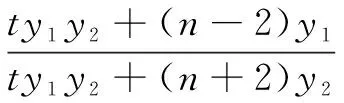
思路3和积关系转化法

思路4第三定义转化法

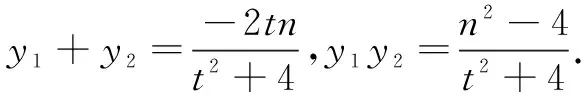
二、迁移应用

解法1(和积关系转化法)

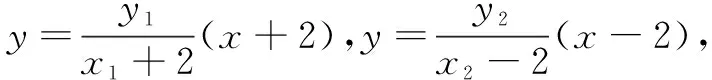
评注本题中积与和的关系很容易确定,再联立直线AM,BN的方程,由结论预见联立消去y可建立关于交点T的横坐标的方程,借助积转化为和的结构化简计算,使问题获解.

解法2(椭圆的定义)

设点A(x1,y1)B(x2,y2),同解法1可得

评注本题与椭圆的顶点有关,类似于引例,可利用椭圆的定义,直接平方后将y替换下来就可以得到对称式,进而用韦达定理可求定值.

评注此解法的关键是面对不对称的代数结构,构造对偶式,实现将代数结构化为对称形式的目的,进而用韦达定理求解参数.