策略得当,大小比较——求解大小比较问题的技巧方法

刘文娥

(山东省青岛西海岸新区第三高级中学)

函数值或参数值的大小比较问题是高考的热点,问题以各种形式创新设置,要求学生合理判断相应的大小关系.此类问题考查的主干知识是幂、指数、对数函数的变形与运算,以及幂函数、指数函数或对数函数的图像与性质的合理应用等,并结合函数与方程、函数与导数、不等式等其他相关知识,综合考查学生的基础知识与基本能力,倍受各方关注.本文对近年高考数学真题进行分析,归纳函数值或参数值大小比较问题的常见方法与基本策略,形成知识网络体系,以期引领与指导数学学习与复习备考.

1 放缩法

例1(2022年全国甲卷文12)已知9m＝10,a＝10m－11,b＝8m－9,则( ).

A.a＞0＞bB.a＞b＞0

C.b＞a＞0 D.b＞0＞a

分析先对指数式与对数式进行互化,再利用对数函数的单调性确定参数m的取值范围,进而根据代数式的结构特征,利用指数函数的单调性,以及指数幂的性质合理放缩处理,最终通过确定两代数式的正负取值情况达到比较大小的目的.

解由9m＝10,可得m＝log910＞log99＝1,而

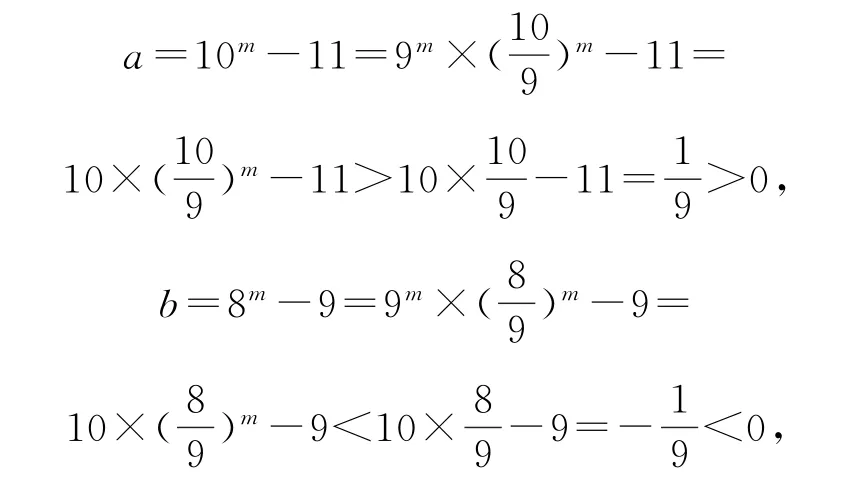
可得a＞0＞b,故选A.

点评利用放缩法处理大小比较问题的关键是先对代数式进行恒等变形与转化,再借助不等式的基本性质、函数的单调性合理放缩、快速判断.

2 利用不等式结论

例2(2022年新高考Ⅰ卷7)设a＝0.1e0.1,b＝,c＝－ln0.9,则( ).

A.a＜b＜cB.c＜b＜a

C.c＜a＜bD.a＜c＜b

分析利用切线不等式(ex≥x＋1,当且仅当x＝0时,等号成立;lnx≤x－1,当且仅当x＝1时,等号成立)、重要不等式(当x＞1时,恒有lnx＜)成立)等相应的“二级结论”进行分析和判断.

综上,c＜a＜b,故选C.

点评利用此方法进行大小比较时,经常借助一些涉及指数与对数、三角函数等方面的不等式结论,以及不等式的基本性质加以求解,体现了函数与不等式等知识之间的综合应用.

3 特殊值法

例3(2020年全国Ⅰ卷理12)若2a＋log2a＝4b＋2log4b,则( ).

A.a＞2bB.a＜2bC.a＞b2D.a＜b2

分析分别将b＝1与a＝4代入题中所给等式,根据等式确定另一参数的取值范围,进而结合题目中给出的相应选项加以合理排除,最终得出所求问题答案.

解由2a＋log2a＝4b＋2log4b,令b＝1,可得2a＋log2a＝4b＋2log4b＝4,可知a∈(1,2),由此可排除选项A,D.令a＝4,可得4b＋2log4b＝2a＋log2a＝18,可知b∈(2,3),由此可以排除选项C.

综上,选B.

点评特殊值法在破解选择题中有一定的用武之地,简单易操作,当然在一些大小比较的问题中也有一席之地,巧妙选取特殊值需要一定的技巧.但利用特殊值法解题具有一定的局限性,要多尝试选取特殊值进行验证.

4 中间值法

例4(2015 年山东卷文2)设a＝0.60.6,b＝0.61.5,c＝1.50.6,则a,b,c的大小关系是( ).

A.a＜b＜c

B.a＜c＜b

C.b＜a＜c

D.b＜c＜a

分析求解本题可先利用不等式、函数的基本性质估算出对应参数a,b,c所对应关系式的变化范围,再选取中间值进行比较,最终给出正确判断.

解 由于0＜b＝0.61.5＜0.60.6＝a＜0.60＝1,c＝1.50.6＞1.50＝1,所以b＜a＜c,故选C.

点评估算法契合《考试说明》中“能根据要求对数据进行估计,并能进行近似计算”的基本精神.特别地,对于大小比较问题,只要合理估算,借助中间值(常见的如0,1等)进行比较,不用直接求出各对应代数式的精确值,可以减化运算,优化解题过程.

5 泰勒展开式法

例5(2022年全国甲卷理12)已知a＝,b＝cos,c＝4sin,则( ).

A.c＞b＞a

B.b＞a＞c

C.a＞b＞c

D.a＞c＞b

分析根据高等数学中的余弦函数、正弦函数的泰勒展开式进行合理放缩,最终确定三者的大小关系.

解根据泰勒展开式

综上,c＞b＞a,故选A.

点评泰勒展开式是高等数学中的相关内容,是高中数学知识的拓展与课外提升部分,是高中数学竞赛中的相关知识点.借助泰勒展开式法进行大小比较,有时能出奇制胜.但此类方法不是高中数学教学和学习的主要内容,只是作为高中数学知识的拓展,给竞赛或学有余力的学生一些知识拓展.

函数值或参数值的大小比较问题,形式多样,但离不开基本的知识点,合理总结破解此类问题的通性通法,掌握基本的破解技巧与策略,进一步落实基础知识、基本技能、基本思想、基本活动经验这“四基”,全面承载函数与方程思想、化归与转化思想、特殊与一般思想,培养抽象概括、推理论证、运算求解能力,提升数学抽象、逻辑推理、数学运算等核心素养.

(完)