深度剖析结构特征,巧妙构造比较大小——2022年新高考Ⅰ卷第7题探究

袁 安

(广东省广州大同中学)

1 试题呈现

题目(2022 年新高考Ⅰ卷7)设a＝0.1e0.1,＝－ln0.9,则( ).

A.a＜b＜cB.c＜b＜a

C.c＜a＜bD.a＜c＜b

本题结构简洁,提供的信息不多,a是指数型函数的值,c是对数型函数的值,学生不能直接计算出各值的大小进而进行比较,各式也没有统一的结构形式,不能构造简单的“同结构”函数应用单调性比较,也不便用中间值法判断,所以本题要对三个式子的整体结构进行分析,巧妙配凑构造函数或放缩进行思考.

本题在知识方面主要考查通过应用导数研究函数的单调性、极值、不等式恒成立等问题.试题需要学生根据各式的特点进行适当的变形,整理成有统一特征的式子后,再构造“同变量”函数进行研究.充分考查学生逻辑推理、推理论证、运算求解等能力,较好地考查函数与导数的核心思想与知识,对于学生运用所学知识,寻找合理解题策略有较高的要求.

2 多视角分析,多方法探究

2.1 作差,构造“同变量”函数

分析通过认真观察,可以发现每个值都可以看作是与0.1 有关的函数值,所以对原式进行重新整理,即a＝0.1e0.1,b＝,c＝－ln0.9＝－ln(1－0.1).根据三个式子的特点构造新函数,用导数工具辅助解决问题.

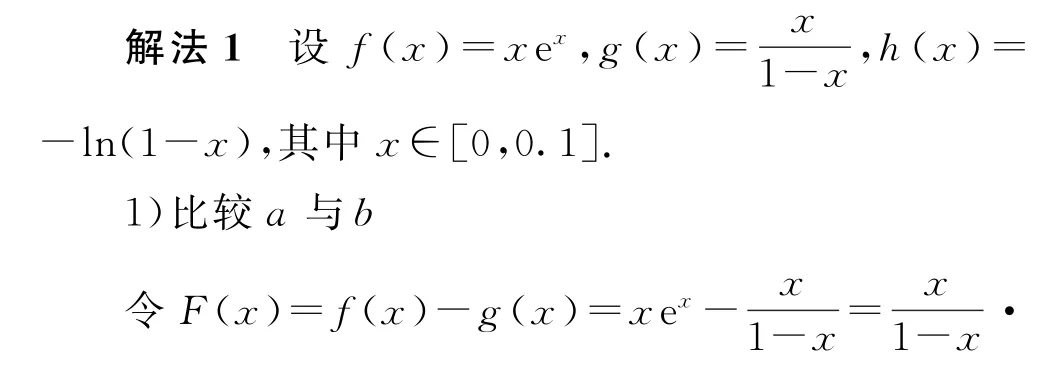
因为k′(x)＝(－x2－2x＋1)ex,当x∈[0,0.1]时,(－x2－2x＋1)＞0,ex＞0,所以k′(x)＞0,k(x)在[0,0.1]上单调递增,故k(x)≥k(0)＝0,G′(x)≥0,从而G(x)在[0,0.1]上单调递增,又G(0)＝0,所以G(0.1)＞G(0)＝0,所以a＞c.

综上,c＜a＜b,故选C.

点评构造“同变量”函数,难点在于需要根据给出的式子特点,通过等价变换,找出它们是哪个函数的函数值.此类问题配凑、构造比较烦琐,有时配凑可能不合理,还需要进行适当的调整并进行再次构造.这能充分考查学生观察、分析问题以及综合应用多种知识研究解决问题的能力,要求学生有较强的数感,同时具备归纳猜想、逻辑推理与推理论证的能力.

2.2 放缩,构造常用不等式

点评放缩法也是比较大小最常用的方法之一.本方法对能力要求较高,要总结出放缩法的常用不等式.

2.3 变换,构造二项展开式

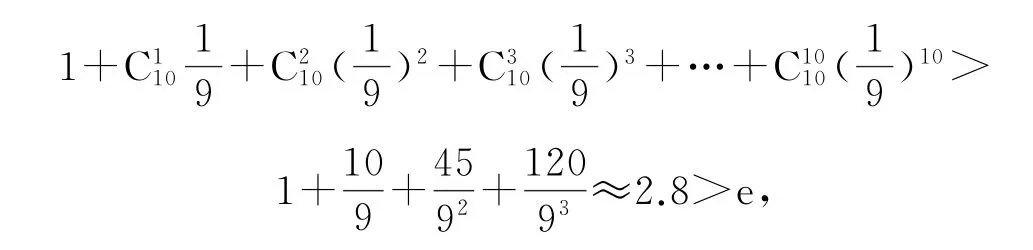
所以a＜b.同理,也可以比较a与c的大小,从而得到c＜a＜b,故选C.

点评通过乘方转化为幂指数结构的式子,再配凑成二项展开式进行放缩也是证明不等式的常用方法.这种方法配凑技巧较强,展开式的计算过程较繁杂,且难度较大.

2.4 估值,构造泰勒展开式

分析本题若使用泰勒展开式来进行估值计算,解题过程更加方便、快捷.

解法4由ex的泰勒展开式,得

点评泰勒展开式是大学数学分析中的内容,用泰勒展开式进行估值时,过程更加简捷,计算相对容易.教师可以将此方法介绍给班级中学有余力的学生,以此激发学生的学习兴趣和求知欲,使学生对大学数学有一定了解,为大学数学学习奠定基础.

常用的指数、对数、正弦、余弦形式的泰勒展开式如下:

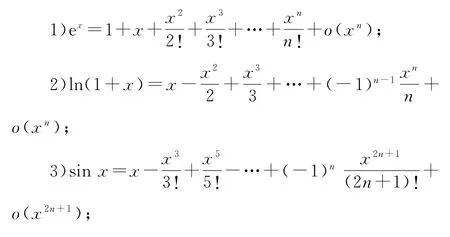
3 试题的再拓展

在实际解题过程中,还有另一类题型:待比较的两个或多个式子的结构形式基本相同,或通过变形整理后结构形式相同.这类题型往往是通过构造“同结构”函数,应用函数的单调性、对称性、极值偏移等方法进行比较.

点评因此构造函数f(x)＝.但本题求导后a,b不在同一个单调区间上,且离极值点的距离比较相近,但不对称,所以用单调性、对称性、极值偏移没有办法解决.观察a,c,它们有相同的变量3,考虑能否再构造“同变量”函数解决问题.

解由题可知,构造函数f(x)＝,则f′(x)＝,所以f(x)在(0,e)上单调递增,(e,＋∞)上单调递减,fmax(x)＝f(e),即c最大,对于a,b,它们不在同一单调区间,不能直接比较大小,再认真分析,可以想办法构造以3为变量的“同变量”函数,即

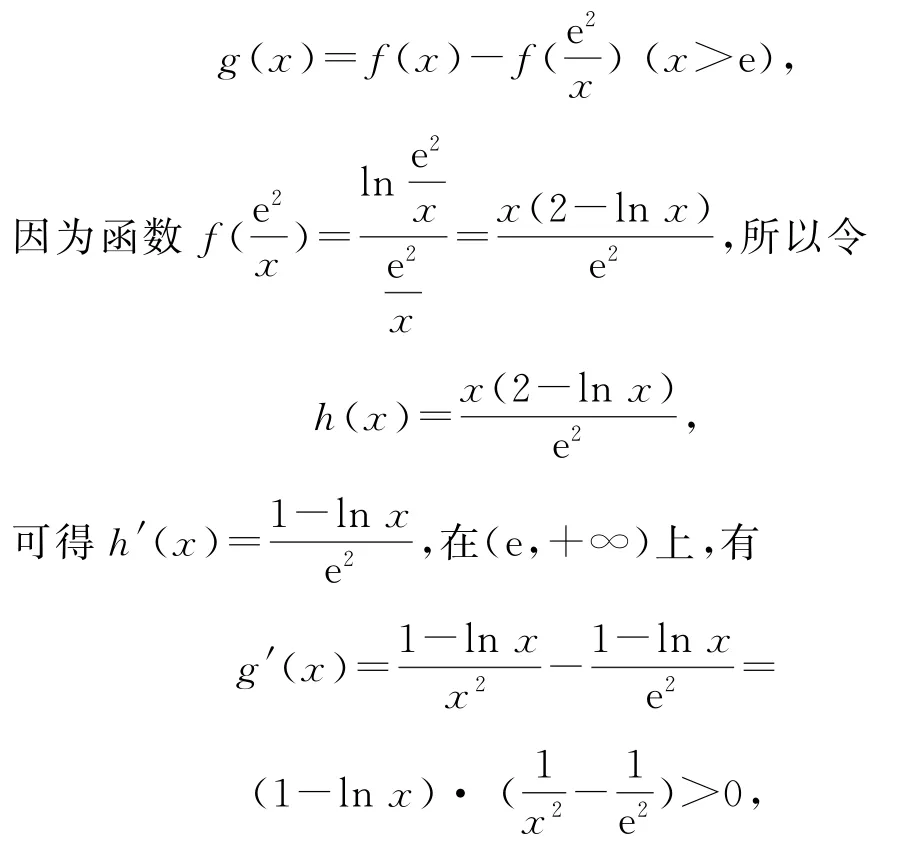
则g(x)单调递增,所以g(3)＞g(e)＝0,从而f(3)－,即b＞a.

综上,c＞b＞a,故选A.

本题结构形式相同,很容易想到构造“同结构”函数,利用单调性解决问题.但实际的解题过程中,发现a,b并不在同一个单调区间,也没办法通过转化与化归的方法把它们转化至同一单调区间来比较大小.通过再观察可以发现a,b两数可以构造成含相同变量3的值,所以想到作差构造“同变量”函数来解决问题.这要求学生对构造法有充分的认识,对学生分析、解决问题能力提出更高的要求.

4 小结

高考试题从命题角度、题型、难度等方面都进行了充分的考量,是知识、方法、思想、能力的具体展现,具有典型性、示范性、指导性的作用,试题蕴含着丰富的背景和数学思想.高考试题除了有选拔功能外,还有良好的教学功能,试题的研究可以帮助我们了解高考方向,把握高考内容和难度.因此我们要深入研究高考试题,领悟试题所蕴含的数学知识和方法,能通过分析、归纳、类比、拓展、猜想、论证等方法把握试题潜在的本质规律,提升学生的核心素养.

(完)