截顶辅助型超聚能射流成形理论及正交优化

葛超，曲卓君，王晋，周晟，胡蝶，余庆波

（北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081）

随着装甲材料及防护技术的飞速发展，对反装甲弹药及相关毁伤技术的发展提出了挑战. 聚能装药结构将炸药爆炸化学能转化为聚能侵彻体（射流、爆炸成形弹丸）动能高效击穿装甲，成为一种重要的反装甲手段并得到了广泛的应用和研究[1-4]. 在此基础上，MININ 等[5]对聚能装药结构进行了系统性优化研究，并首次提出了超聚能装药的概念.

截顶辅助型超聚能装药结构是最具应用前景的超聚能装药结构，众多学者对其进行了大量研究.MININ 等[6-8]对超聚能射流进行了理论研究与数值模拟，结果表明超聚能射流质量始终大于杵体质量，射流头部速度相对传统射流提高了25%～30%，并通过X 光试验对仿真结果进行了验证. 王成等[9]、王淦龙等[10]采用数值方法研究了药型罩结构对超聚能射流轴向速度分布和动能的影响. 胡晓敏等[11]、石军磊等[12]以及孙建军等[13]、畅博等[14]研究了辅助药型罩材料对超聚能射流性能和侵彻能力的影响. 张程健等[15]利用灰色关联理论分析了聚能装药辅助药型罩材料、辅助药型罩厚度、截顶药型罩锥角和厚度4个因素与超聚能射流成形的关联度. 徐文龙等[16]基于准定常理论，揭示了超聚能成形机理，并通过数值仿真进行了验证. 研究结果均表明，相比传统的锥形装药结构，超聚能装药成形的超聚能射流在侵彻毁伤效应方面，体现出显著优势.

目前，国内外学者关于超聚能装药结构的研究，主要聚焦于超聚能射流成形理论、超聚能装药结构优化. 但针对截顶辅助型超聚能装药结构，在射流成形理论方面，忽略了装药、壳体等因素影响，未考虑冲击波传播至辅助药型罩与截顶药型罩的时间间隔问题，无法准确描述超聚能射流成形过程；在射流成形影响因素方面，对药型罩材料、厚度等单一因素影响研究较多，但对多因素耦合作用的影响研究较少，尤其是各因素影响的显著性及主次关系揭示方面，尚处于空白，制约了截顶辅助型超聚能装药结构的优化设计及应用.

本文针对以上问题，基于射流成形阶段划分，建立了截顶辅助型超聚能射流成形微元法理论模型；综合考虑药型罩、炸药、壳体等影响因素，建立了超聚能射流成形特性主控参量量纲一分析模型；最后通过正交优化方法，揭示了辅助药型罩厚度、辅助药型罩边缘凸出长度、截顶药型罩壁厚、锥角以及炸高对超聚能射流有效射流长度和头部速度的影响规律，为截顶辅助型超聚能装药结构武器化应用提供了有益指导.

1 截顶辅助型超聚能射流成形理论

截顶辅助型超聚能装药基本结构如图1 所示. 装药长度为l，辅助药型罩为圆柱形平板，密度为ρ1，壁厚为δ1，直径为D1，边缘凸出截顶药型罩长度为Δ；截顶药型罩密度为ρ2，壁厚为δ2，口径为D，截顶直径为D2，锥角为2α（α＜90°）.

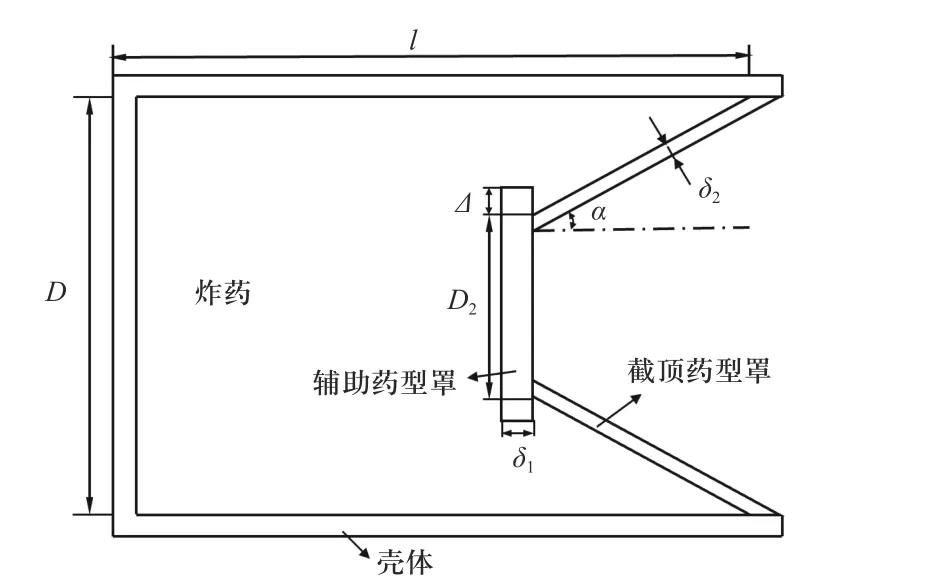
图1 截顶辅助型超聚能装药结构Fig. 1 Structure of trunconical hypercumulation shaped charge

截顶辅助型超聚能装药结构形成射流基本可分为3 个阶段，如图2 所示：第一阶段，装药起爆后，截顶辅助药型罩首先受爆轰波压力作用，获得速度vf；第二阶段，受辅助药型罩和爆轰波联合作用，截顶药型罩与辅助药型罩碰撞角为π/2+β，形成具有较大质量的射流，沿辅助药型罩内壁流动，如图2（a）所示.此时，射流速度、质量分别为，杵体速度、质量分别为；紧接着，射流运动到中轴线后发生二次碰撞，碰撞角为π-γ，大于90°，形成高速高质量的超聚能射流，如图2（b）所示，此时射流速度、质量分别为vj，mj，杵体速度、质量分别为vs，ms；第三阶段，随着射流不断积聚以及射流与辅助药型罩速度梯度增大，后续射流并未与辅助药型罩发生碰撞，成形过程与传统射流形成过程类似. 此阶段所形成射流的速度与质量分别为v杵体速度与质量分别为.

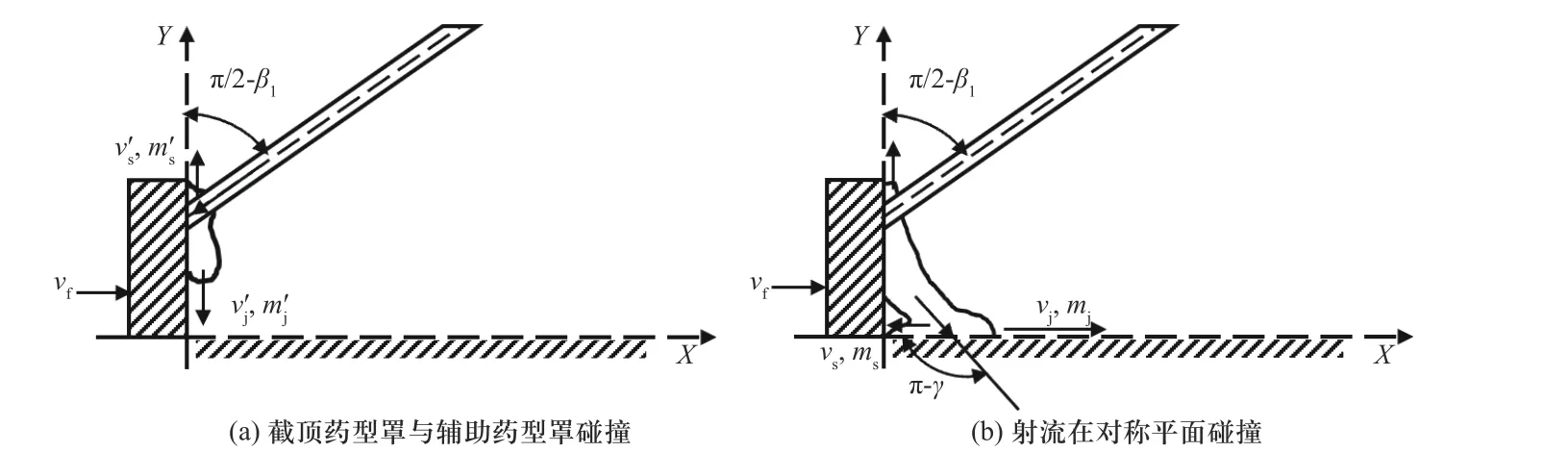
图2 截顶辅助超聚能射流形成过程示意图Fig. 2 Schematic diagram of the formation process of trunconical hypercumulation jet

在理想条件下，爆轰波首先传播至辅助药型罩，受边缘凸出长度影响，辅助药型罩无法自由运动，设阻力系数为f(Δ). 综合考虑炸药、辅助药型罩，由Gurney 平板压垮理论[17]可获得辅助药型罩沿X轴运动速度vf为

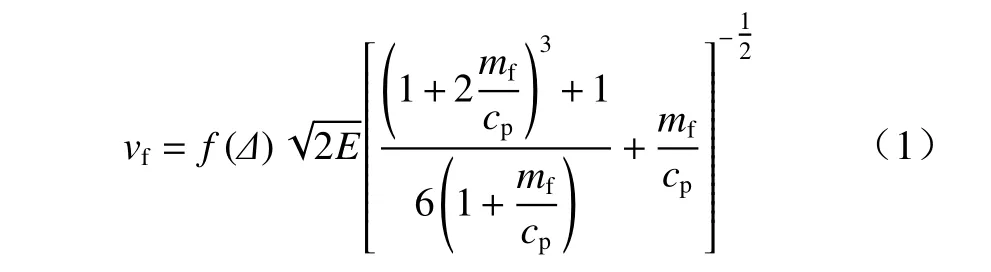
靠近顶端的一小部分截顶药型罩先后与辅助药型罩和对称轴碰撞，形成超聚能射流. 选取各微元平均压垮速度作为此部分的压垮速度. 由定常射流理论，截顶药型罩的压垮角为

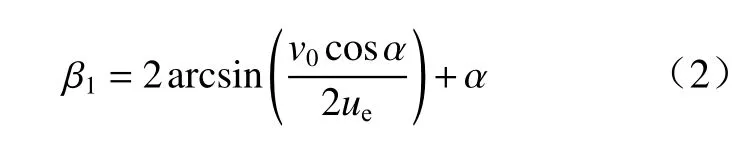
式中ue为爆轰波经过药型罩表面的速度.

结合文献[16]可得超聚能射流部分射流与杵体速度为

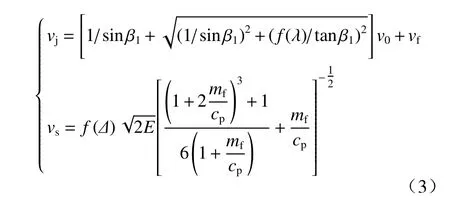
超聚能射流部分射流质量mj及杵体质量ms为

式中：f(λ)为射流沿辅助药型罩运动时的速度损失系数；m2为形成超聚能射流部分的截顶药型罩质量.

而当截顶药型罩被压垮至某一程度后，截顶药型罩开始不与辅助药型罩相碰撞，直接压合汇入射流形成普通射流部分. 对于此部分射流成形过程，可由准定常理论进行描述. 此部分射流和杵体的速度分别为

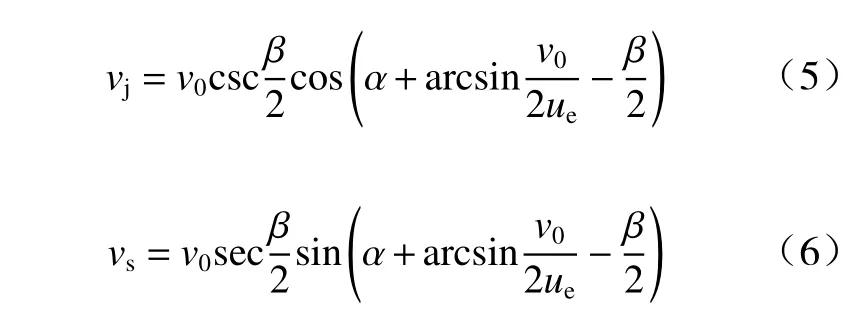
依据动量和质量守恒定理可求得射流和杵体的质量表达式. 设药型罩微元质量为dm，dmj和dms分别为射流和杵体的质量，则dm=dmj+dms.

由于准定常理论中未知变量的数量多于独立方程式的数量，因此须引入一个公式使方程式封闭.压垮速度v0计算模型如图3 所示，将截顶药型罩划分为若干微元，同时受径向与轴向2 个方向炸药作用，则

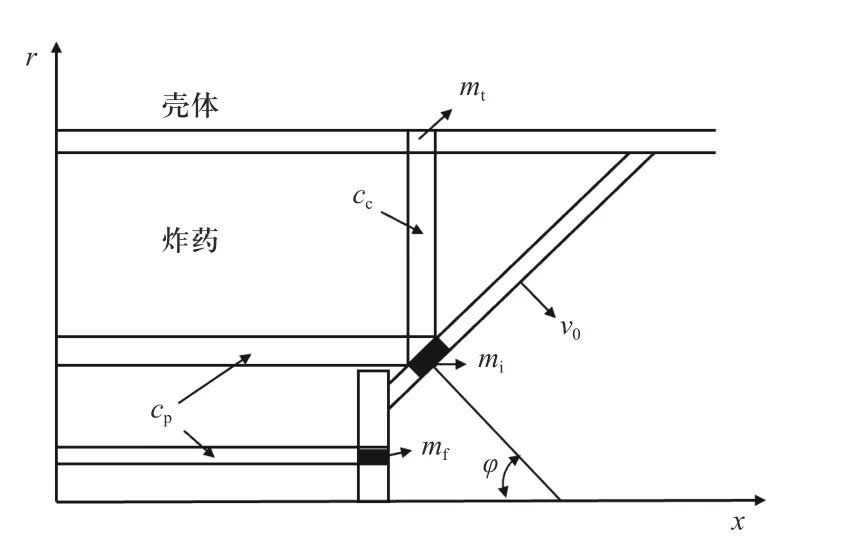
图3 药型罩压垮速度计算模型Fig. 3 Calculation model of liner collapse velocity

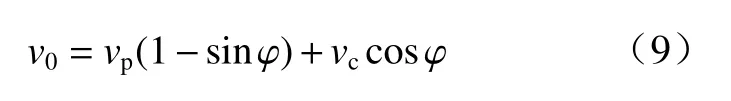
式中： φ为药型罩微元处切线的法线与对称轴线的夹角；vp为微元对于轴向装药产生的压垮速度分量；vc为微元对径向装药产生的压垮速度分量.

由Gurney 平板压垮公式和Chanteret 管柱压垮公式[14]分别获得vp和vc：

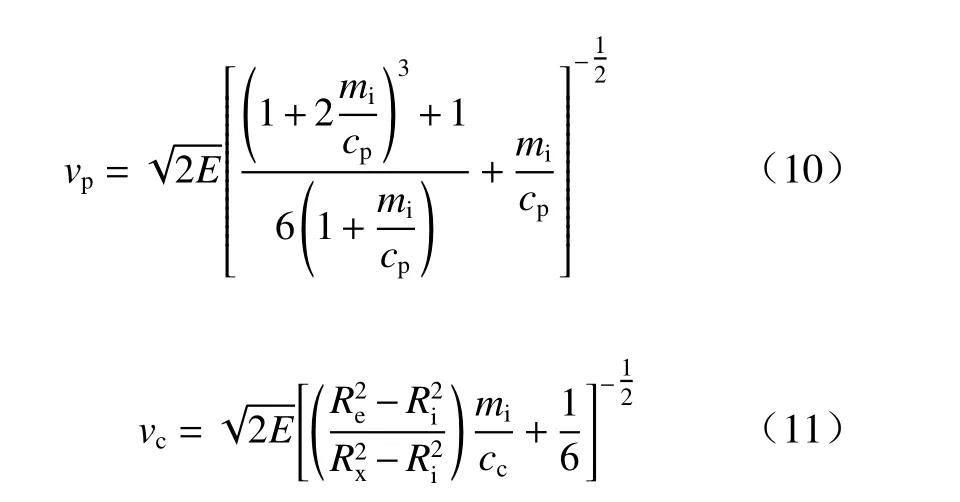
式中：Re为药型罩微元对应装药的外半径；Ri为药型罩微元对应装药的内半径；Rx为药型罩微元对应装药的刚性面半径；mi、mt和cc分别为截顶药型罩微元质量、壳体微元质量及装药径向微元质量，则Rx可通过求解下式获得：

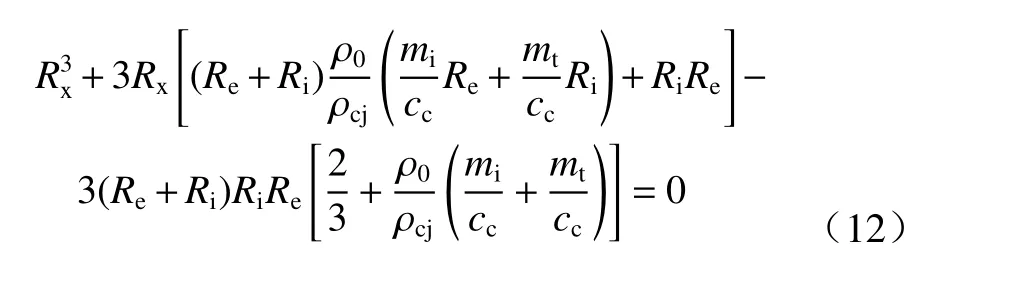
2 主控参量对超聚能射流成形特性影响

2.1 超聚能射流成形主控参量分析

通过理论分析可知，截顶辅助型超聚能装药结构中各组成部分对超聚能射流成形都有不同程度的影响，现从装药、辅助药型罩、截顶药型罩以及壳体等结构方面分别进行分析. 影响超聚能射流成形的主要因素有：

①装药方面：装药口径（D），装药长度（l），装药密度（ρ）；

②辅助药型罩方面：厚度（δ1），边缘凸出长度（Δ），材料密度（ρ1）；

③截顶药型罩方面：锥角（2α），壁厚（δ2），材料密度（ρ2），截顶直径（D2）；

④壳体方面：壁厚（δ3），材料密度（ρ3）.

除此之外，药型罩底端与靶板之间的距离H（炸高）对侵彻结果具有直接影响，通常存在一个最佳炸高. 因此炸高H也应作为一个影响超聚能射流成形的主要因素.

因此，超聚能射流速度vj可表示为如下函数关系式：

选取ρ2、δ2为基本量，根据量纲分析П定理，对式（13）进行量纲一化，得

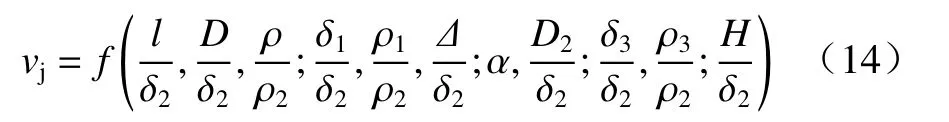
在不改变炸药、辅助药型罩、截顶药型罩及壳体材料的情况下，关于材料性能的参数自行满足相似条件，式（14）可简化为

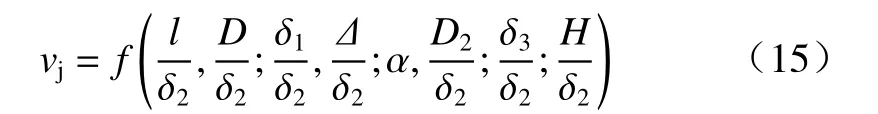
在上述分析基础上，可以得到8 个与超聚能装药结构性能和射流特性相关的量纲一量. 通过试验或仿真模拟，即可获得各量纲一量对超聚能射流成形的影响规律.

2.2 典型超聚能射流成形过程

采用Autodyn 建立二维轴对称模型，由于模型涉及多种材料的大变形和大位移，采用Autodyn 高精度多物质求解器Euler-2D 进行求解. 超聚能装药基本结构与计算模型如图4 所示. 其中，装药直径为80 mm，装药长度为120 mm，壳体壁厚为2 mm. 选用钨作为辅助药型罩材料，厚度5 mm，边缘凸出截顶药型罩外缘1 mm. 截顶药型罩材料为铜，壁厚2 mm，于1/3 处截顶. 起爆方式选择中心点起爆.

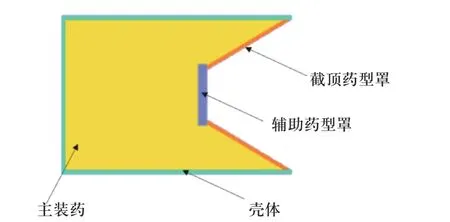
图4 超聚能装药结构数值计算模型Fig. 4 Numerical model of trunconical hypercumulation shaped charge

计算中对金属材料的变形行为选用Shock 状态方程进行描述，装药选用JWL 状态方程，数值模拟中所使用材料均来自于Autodyn 材料库，药型罩、壳体及装药材料参数取值如表1 及表2 所示.

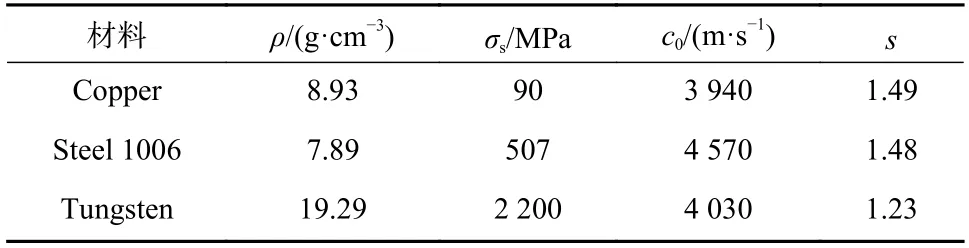
表1 装药结构主要材料参数Tab. 1 Material parameters of charge structure

表2 B 炸药JWL 状态方程主要参数Tab. 2 Parameters of JWL equation of state of COMP B

超聚能射流形成过程压力分布如图5 所示. 装药起爆后，在约10 μs 时，爆轰波首先到达辅助药型罩所在位置并推动其发生运动，如图5（a）所示. 在爆轰波继续作用下，截锥药型罩开始坍塌，与辅助药型罩碰撞，并沿辅助药型罩的接触面流动，如图5（b）所示. 当流动至药柱轴线时，药型罩发生二次碰撞并继续坍塌，开始形成超聚能射流，如图5（c）所示. 在辅助药型罩作用下，杵体初始质量小，且存在较大的反向速度，而射流质量大且在辅助罩作用下显著增强.随着射流不断积聚及射流与辅助药型罩速度梯度增大，后续射流并未与辅助药型罩发生碰撞，且辅助药型罩对后续射流影响较小，后续射流成形过程与传统射流形成过程类似，射流进一步拉伸，形成高速细长射流. 结果表明，超聚能射流成形过程与上述理论分析过程基本一致.

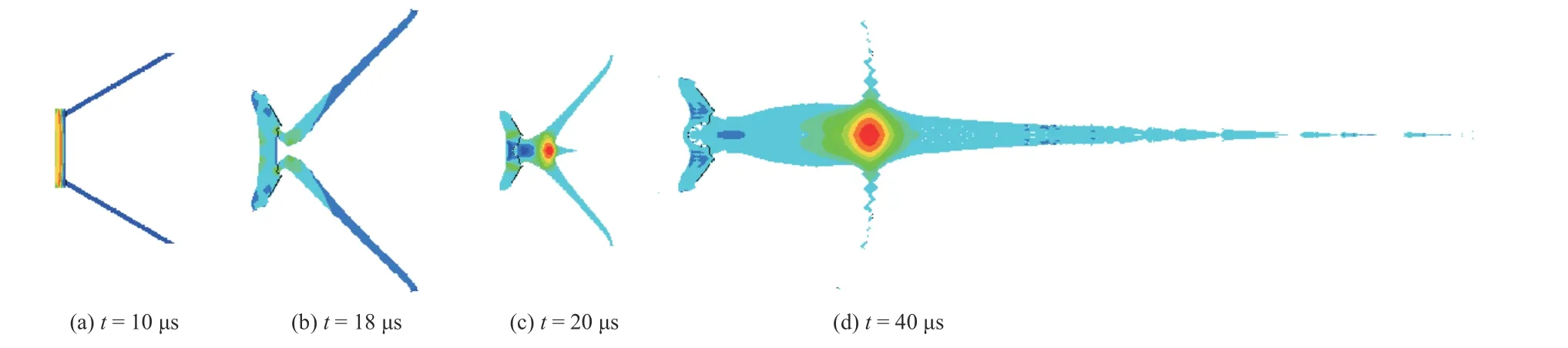
图5 典型超聚能射流成形过程Fig. 5 Typical formation process of hypercumulation jet

2.3 主控参量对超聚能射流成形特性的影响对比

以超聚能射流成形主控参量为基本参数，研究了δ1/δ2、Δ/δ2、α3 个与药型罩相关的主控参量对超聚能射流成形特性的影响，保持3.1 节中其他结构参数不变，通过设计辅助药型罩与截顶辅助药型罩的厚度控制参量δ1/δ2、辅助药型罩半径凸出截顶药型罩外缘长度控制参量Δ/δ2、锥角α对超聚能射流成形影响.

40 μs 时超聚能射流轴向速度分布如图6 所示.定义速度于3 km/s 以下为低速区，速度于3～6 km/s为中速区，6 km/s 以上则为高速区. 从图6（a）中可以看出，随着量纲一量δ1/δ2的增大，射流低中速部分速度逐渐降低，射流头部速度则随之增大. 此外，射流长度先增大后减小. 由图6（b）可知，辅助药型罩边缘凸出长度对射流整体影响较小，仅对射流头部速度一定影响. 由图6（c）可知，随着锥角的增大，射流各部分速度逐渐减小. 且高、中速射流长度逐渐变短，相应的，低速段明显变长. 另外，射流头部部分区间速度随锥角增大而出现较大波动，说明射流前端产生较多断裂间隙. 前面分析了辅助药型罩厚度、边缘凸出长度、截顶药型罩壁厚和锥角控制下的量纲一量对射流速度分布的影响.

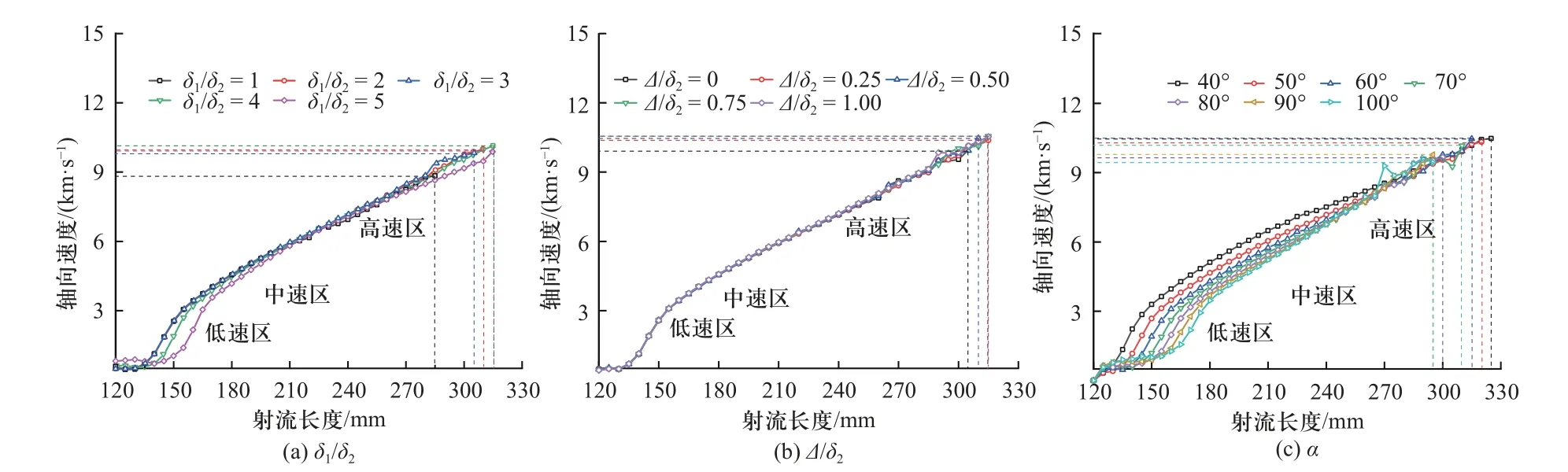
图6 射流速度分布曲线Fig. 6 Jet velocity distribution

图7～图9 为1.5D炸高处，射流头部速度与量纲一量δ1/δ2、Δ/δ2、α间的关系曲线. 由曲线可知，射流头部速度随量纲一量δ1/δ2、Δ/δ2的增大而增大，随量纲一量α的增大而减小.

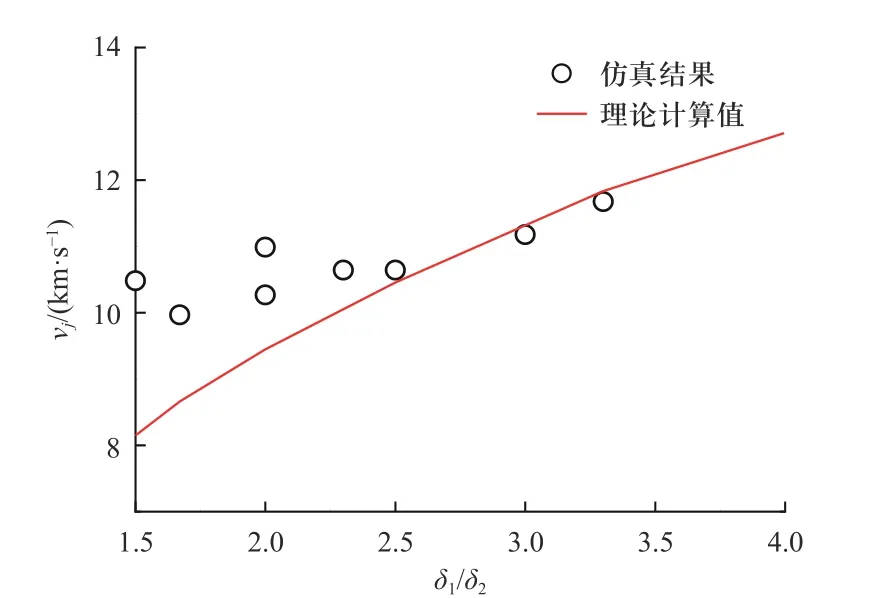
图7 射流头部速度与量纲一量δ1/δ2 的关系Fig. 7 Jet tip velocity versus dimensionless quantity δ1/δ2

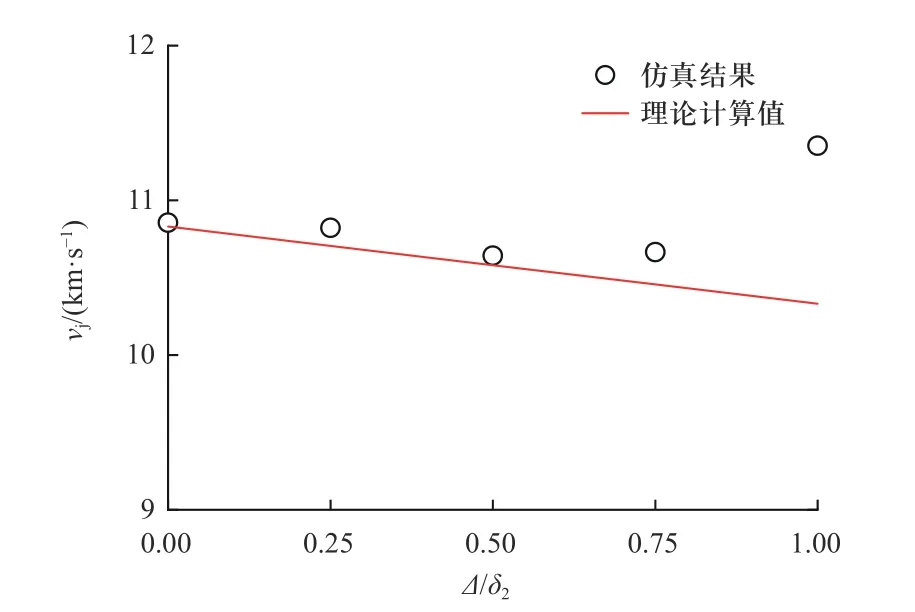
图8 射流头部速度与量纲一量Δ/δ2 的关系Fig. 8 Jet tip velocity versus dimensionless quantity Δ/δ2

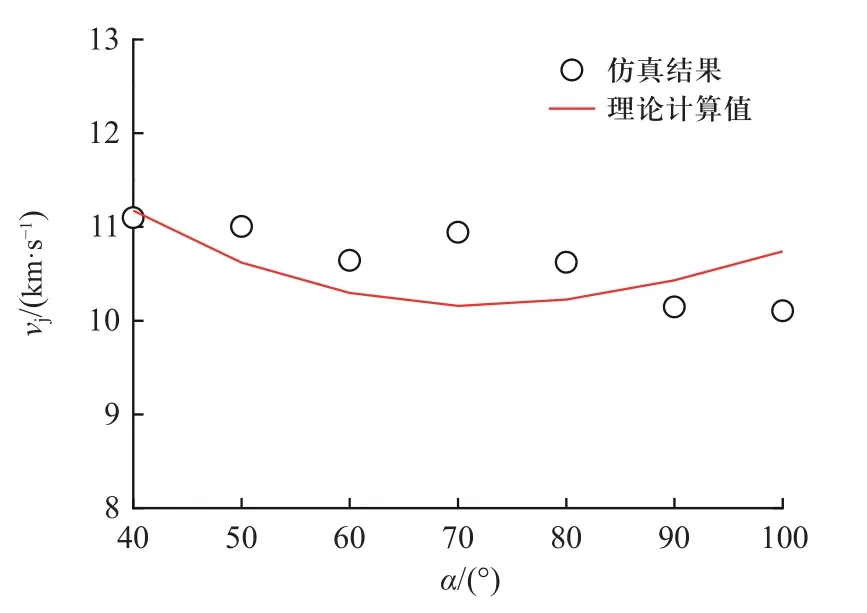
图9 射流头部速度与量纲一量α 的关系Fig. 9 Jet tip velocity versus dimensionless quantity α

3 超聚能装药结构优化设计

3.1 正交优化设计

由上文分析可知，辅助药型罩厚度、边缘凸出长度、截顶药型罩壁厚、锥角等因素均会对射流速度分布、射流头部速度等产生显著影响. 但在多因素共同作用下，各因素影响的显著性还需进一步分析. 通过正交优化方法，结合炸高分析上述4 种因素影响射流主要指标的主次关系，选取截顶辅助型超聚能装药结构优化设计指标：射流头部速度vj与有效射流长度L，如图10 所示. 以3 km/s 作为射流末端的临界破甲速度，将射流末端临界破甲速度点与射流头部速度点之间各段断裂射流长度之和称为有效射流长度.

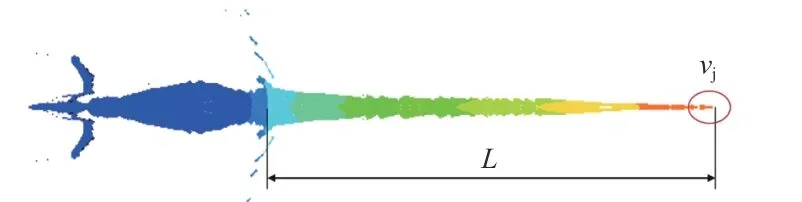
图10 射流头部速度vj 与有效射流长度LFig. 10 Tip velocity vj and effective jet length L

分别选用截顶药型罩锥角（A）、壁厚（B）、辅助药型罩厚度（C）、辅助药型罩边缘凸出长度（D）和炸高（E）作为正交优化参数，各因素设置4 个水平，如表3所示，采用L16(45)正交表来设计仿真分析方案，共计16 组，如表4 所示.

表3 正交试验因素水平表Tab. 3 Factor level table of orthogonal test

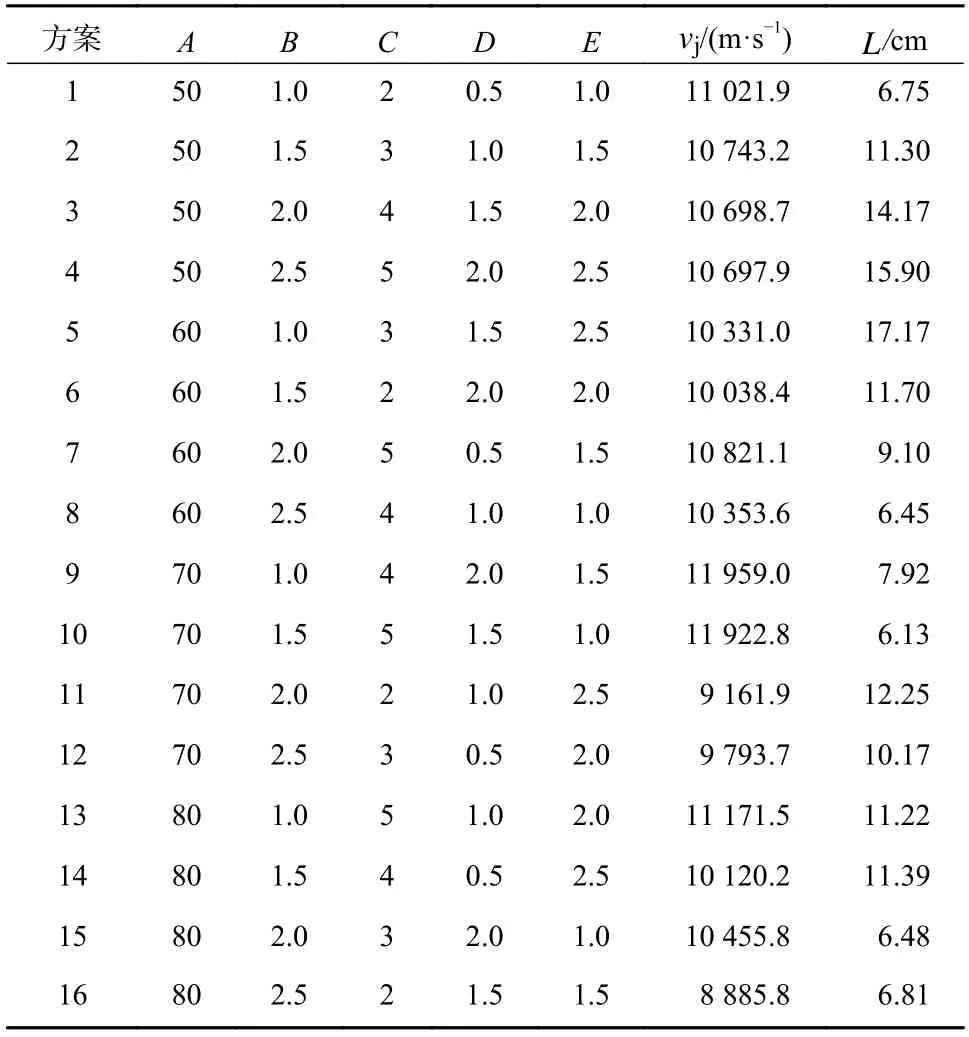
表4 正交试验方案及试验结果表Tab. 4 Orthogonal experimental scheme and results

3.2 正交优化结果及分析

分别对表4 所列的16 组正交试验方案进行数值模拟，得到射流头部速度vj和有效长度L.

正交试验的极差分析结果列于表5，射流头部速度与有效射流长度和各因素4 水平之间的关系如图11所示. 由分析结果可知，第9 组射流头部速度最大：vj=11 959.0 m/s，对应的试验组合为A3-B2-C3-D4-E2；第4 组的有效射流长度最长：L=15.9 cm，对应的试验组合为A1-B4-C4-D4-E4. 综合图11，分析极差可知，5 因素对射流头部速度影响的主次顺序为：辅助药型罩厚度（C）→截顶药型罩壁厚（B）→炸高（E）→截顶药型罩锥角（A）→辅助药型罩边缘凸出长度（D）；5 因素对有效射流长度影响的主次顺序为：辅助药型罩边缘凸出长度（D）→炸高（E）→截顶药型罩锥角（A）→辅助药型罩厚度（C）→截顶药型罩壁厚（B）.

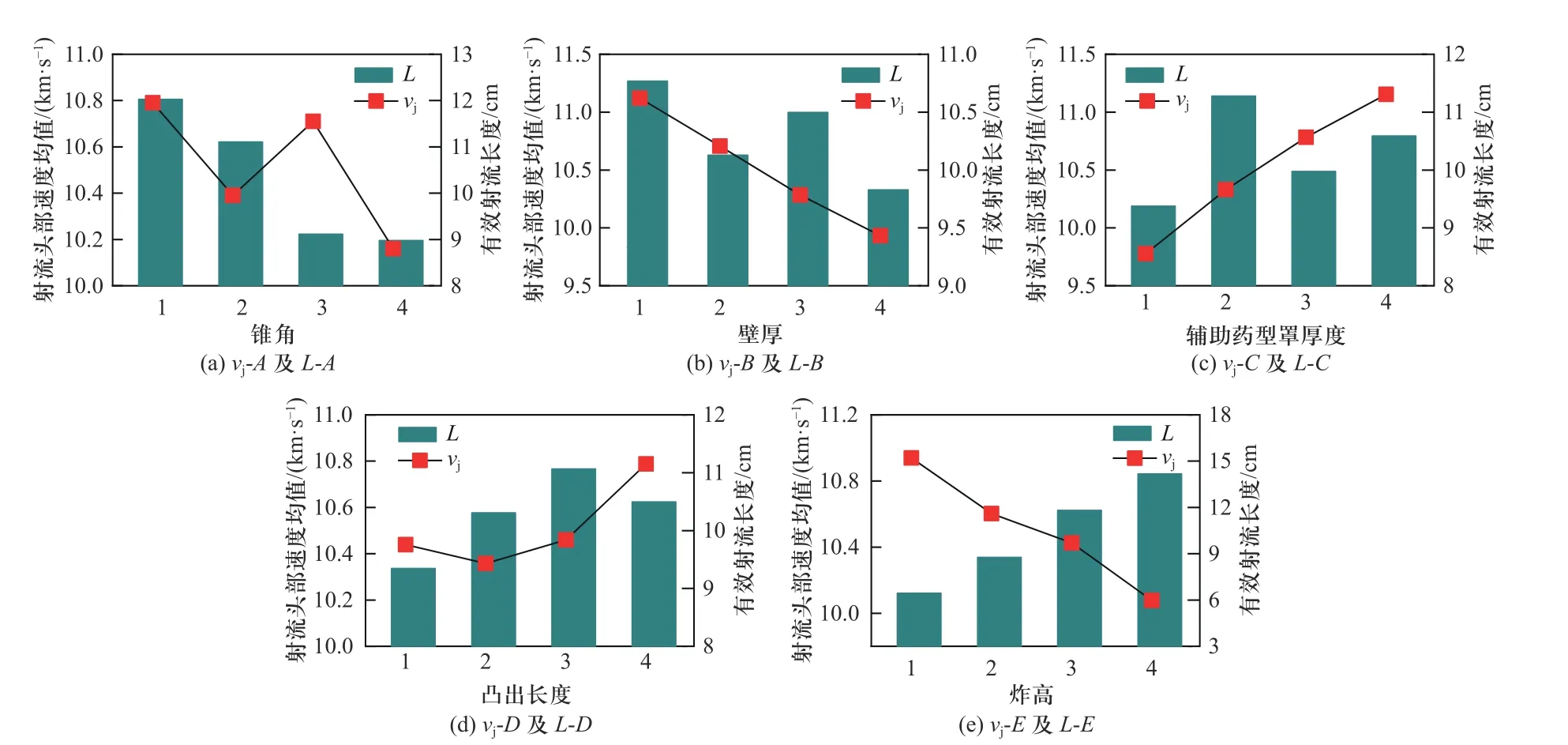
图11 射流头部速度、有效长度与4 水平之间的关系趋势Fig. 11 Curves of the mean value of jet head velocity and the mean value of jet effective length and four levels

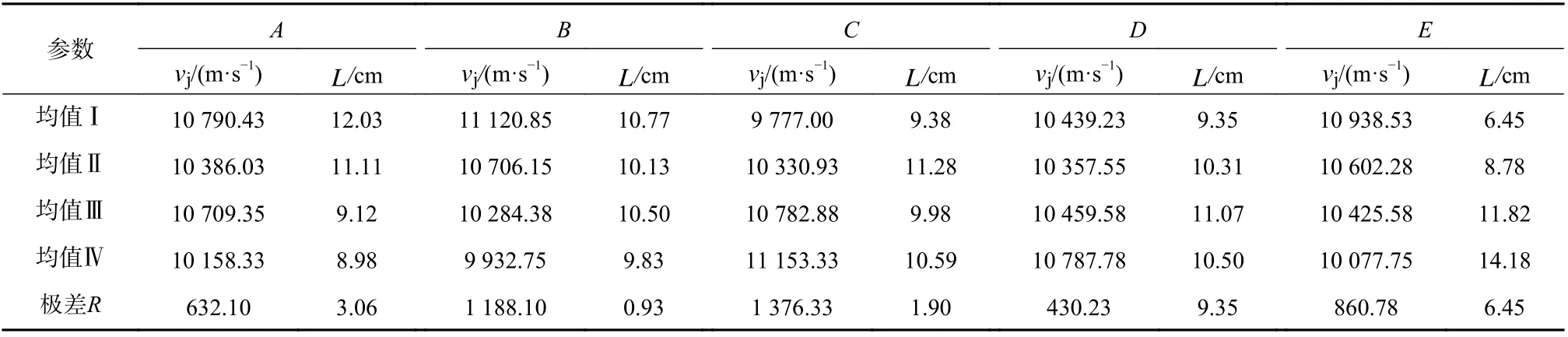
表5 极差分析表Tab. 5 Range analysis

根据极差分析结果优化截顶辅助型超聚能结构参数，由于主要因素的水平变化对射流指标的影响较大，须选择最优水平，其余次要因素根据实际情况选择合适的水平. 据此，针对射流头部速度和有效射流长度共选取了4 种优化后的因素水平组合，分别为A1-B1-C4-D4-E1，A3-B1-C4-D4-E1，A1-B1-C2-D3-E4，A1-B3-C2-D3-E4.分别对其进行数值模拟，计算结果列于表6.

由表6 可以看出，综合考虑射流的头部速度与有效长度，最优水平应为组合3（A1-B1-C2-D3-E4），即截顶药型罩锥角为50°，壁厚1 mm，辅助药型罩厚度3 mm，凸出截顶药型罩顶部边缘1.5 mm 的超聚能装药结构在2.5 倍口径炸高处形成射流性能最优.

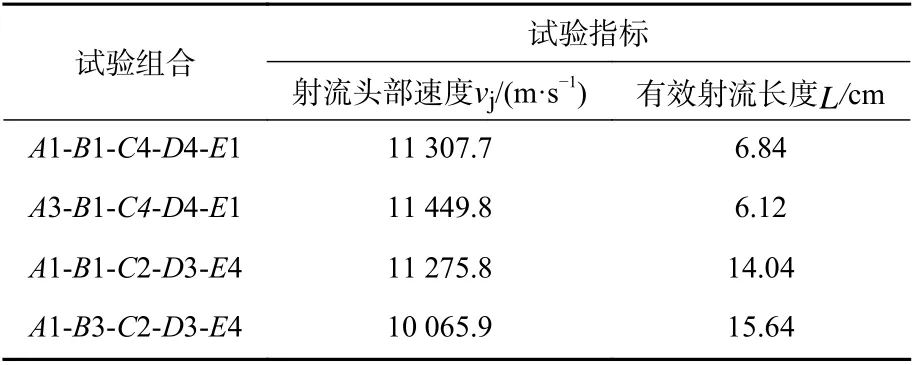
表6 优化后组合的模拟结果Tab. 6 Simulation results of optimized combination

4 结 论

通过对截顶辅助型超聚能装药结构的研究分析，可得到如下结论：

①基于传统射流理论，采用微元法，综合考虑药型罩、炸药、壳体等影响因素，建立了截顶辅助型超聚能射流成形理论计算模型.

②对影响超聚能射流成形特性的主控参量进行了量纲分析. 射流头部速度随量纲一量δ1/δ2、Δ/δ2的增大而增大，随量纲一量α的增大而减小.

③采用数值模拟方法对截顶辅助型超聚能装药结构进行了正交优化设计研究，结果表明，5 因素对射流头部速度影响的主次顺序为：辅助药型罩厚度→截顶药型罩壁厚→炸高→截顶药型罩锥角→辅助药型罩边缘凸出长度；4 因素对有效射流长度影响的主次顺序为，辅助药型罩边缘凸出长度→炸高→截顶药型罩锥角→辅助药型罩厚度→截顶药型罩壁厚.

④得到优化后的装药结构方案组合为：锥角50°，壁厚1 mm，辅助药型罩厚度3 mm，凸出截顶药型罩顶部边缘1.5 mm，其在2.5 倍炸高处形成射流性能较好.