高超声速圆锥边界层转捩反转数值研究

2022-10-26雷娟棉曹家伟

北京理工大学学报 2022年10期

雷娟棉，曹家伟

（北京理工大学宇航学院，北京 100081）

高超声速边界层从层流到湍流的转捩问题是空气动力学领域的难点和热点问题之一，边界层转捩后飞行器表面的摩擦阻力系数、热流会急剧上升，对整个飞行器的气动力、气动热特性产生重要影响，进而影响着飞行器的飞行效率和飞行安全[1]. 因此，关于边界层转捩问题的研究一直是空气动力学领域的研究热点. 在相关的风洞实验、数值模拟计算、理论分析中，已探明主要原因的转捩现象和转捩规律被认为是一般性结论，而与一般性结论中的转捩趋势相反的现象被称为转捩反转[2]. 圆锥体外形作为高超声速飞行器的典型常用外形，被广泛应用于边界层转捩问题研究. 目前，已有部分实验研究结果表明，在某些情况下圆锥表面边界层呈现转捩反转的现象，但关于边界层转捩反转的认识非常有限，边界层转捩反转现象仍然是目前转捩研究中尚未探明原因的一个重要问题[3].

对细长圆锥边界层转捩行为最早、最全面的研究之一是STETSON[4]在1967 年进行的风洞实验研究，实验研究结果表明当圆锥攻角从0°开始增大时，其背风面边界层转捩位置向前移动，而迎风面边界层转捩位置向后移动，在有攻角条件下圆锥表面的转捩阵面呈现为背风面转捩位置靠前、迎风面转捩位置靠后的周向不对称分布，该现象被认为是圆锥边界层转捩典型的一般性规律. 在某些情况下，亦有可能出现圆锥迎风面与背风面转捩位置同时前移的现象，但背风面转捩前移的幅度要大于迎风面，使转捩阵面沿周向呈现同样的非对称特性分布规律.MUIR 等[5]在1972 年的风洞实验中发现当圆锥头部钝度增大到特定尺度时，在高雷诺数条件下圆锥迎风面转捩位置随攻角增大而向前运动，而背风面转捩位置先向后运动再向前运动，整体呈现出随攻角增大迎风面转捩先于背风面转捩的边界层转捩反转现象. 陈久芬等[6]在对7°尖锥的红外测量转捩实验中发现当攻角α从8°增大到10°时，迎风面转捩位置从推迟变为提前，在部分攻角条件下发生了边界层转捩“逆转”的现象.

早在20 世纪60 年代，在风洞实验中便发现了圆锥的钝度变化引起转捩位置反转现象，即在小范围内增大锥体头部钝度，转捩位置向下游移动；然而当锥体头部钝度增大到某一临界值时，转捩位置随钝度增加由推迟转变为提前. 之后，PARADES 等[7]通过在圆锥头部增加粗糙带的实验方法发现圆锥钝锥边界层转捩对头部粗糙度十分敏感，认为转捩提前的原因是随着头部钝度增大圆锥表面对于粗糙度的敏感性增强，从而促进了转捩提前. 陈苏宇等[8]在FD-14A 激波风洞中通过实验在不同马赫数下研究了圆锥边界层转捩钝度反转的现象，复现了“Λ”型和“N”型两类反转，并且通过功率谱密度分析，从熵层影响边界层结构的角度分析了圆锥钝度反转的原因. 陈坚强等[9]从钝前缘的感受性以及熵层效应两个角度初步分析了钝度反转产生的可能原因.

目前对于边界层转捩反转现象的认识主要是基于有限的风洞实验结果，但由于转捩试验难度大、影响因素多且费用高，很难开展大量系统性的转捩反转研究. 而在各种转捩预测方法中，基于雷诺平均NS (RANS)方程的转捩预测模型方法具有计算稳定、求解效率高等优点，已在高超声速边界层转捩预测中得到了广泛应用[10]. 杨云军等[11]利用基于k-ω湍流模型耦合的转捩模型在高超声速小攻角条件下对圆锥的典型非对称转捩进行了预测，分析了非称转捩效应下的圆锥气动力特性. 蔡林峰等[12]通过基于SSTk-ω湍流模型耦合的γ转捩模型，在添加可压缩性修正后，具备预测高超声速流动转捩的能力. 王卫星等[13]在针对Ma=4.5 的锥型曲面进气道进行数值模拟时发现，随着锥尖钝度增加，边界层转捩呈“推迟-提前-推迟”的转捩反转现象.

因此，本文通过求解基于SSTk-ω湍流模型耦合γ转捩模型的RANS 方程，并进行可压缩性修正，对高超声速圆锥边界层转捩的攻角反转和钝度反转问题进行数值模拟研究. 旨在通过数值模拟方法研究高超声速圆锥边界层转捩位置随攻角、头部钝度变化出现的边界层转捩反转现象，通过不同条件下转捩位置的变化规律及对流场的影响，对比分析转捩反转与正常一般性转捩规律的流动特点，为高超声速飞行器边界层转捩、特别是转捩反转研究提供支撑.

1 数值模拟方法

1.1 基本数值方法

本文数值研究采用有限体积法求解定常可压缩RANS 方程组，时间推进采用隐式格式，无黏通量采用Roe-FDS 格式，黏性通量采用中心差分格式进行离散.

1.2 γ 转捩模型

本文数值模拟计算采用的湍流模型为SSTk-ω湍流模型，利用MENTER 等[14]根据实验数据重新得到的Reθc经验关系式，加入间歇因子输运方程，封闭成一方程γ转捩模型. SSTk-ω[15]模型建立了湍流流体中湍动能k和比耗散率ω的输运方程：

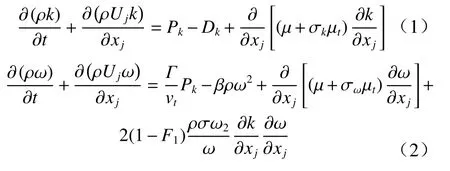
式中Pk和Dk分别为湍动能的生成项和耗散项.

SSTk-ω模型不能预测层流流动的原因是Pk和Dk无法判别边界层流动状态. 在SSTk-ω模型的基础上建立间歇因子γ输运方程并作用于Pk和Dk，从而实现对流动中从层流到湍流转捩过程的数值模拟.γ输运方程：

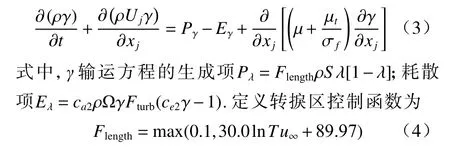
利用MENTER 提出的Reθc与当地压力梯度λθ和当地湍流度TuL的经验关系式，从而避免了建立Reθc的输运方程：

利用文献[16]给出的基于来流马赫数的可压缩性修正方法，针对高超声速可压缩流转捩问题进行可压缩修正. 基于当地马赫数，对临界动量厚度雷诺数进行修正，具体形式如下：

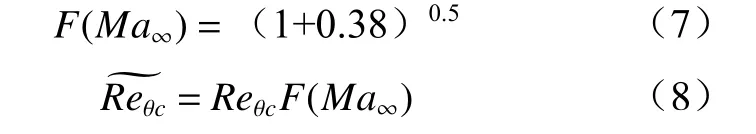
1.3 计算外形与边界条件

本文数值模拟计算的外形为圆锥体，图1 为计算外形示意图，其中Rn为圆锥头部钝度半径，θ为圆锥的半锥角，L为圆锥长度，坐标系的原点取圆锥的头部顶点. 模型头部钝度Rn、半锥角θ、锥长L随下文中不同研究条件而有所变化. 定义周向角φ为纵向对称面与周向位置顺时针的夹角，背风面子午线φ=0°. 计算域选取圆锥前向距离为0.2 倍锥长,法向距离为2 倍底部半径的流场范围. 采用结构化网格对圆锥流场进行离散，由于圆锥为对称外形，为了减小计算量取半模进行计算. 图2 为计算网格示意图. 壁面采用无滑移等温壁面条件，来流条件为自由来流远场边界条件，底部为超声速外推边界条件.

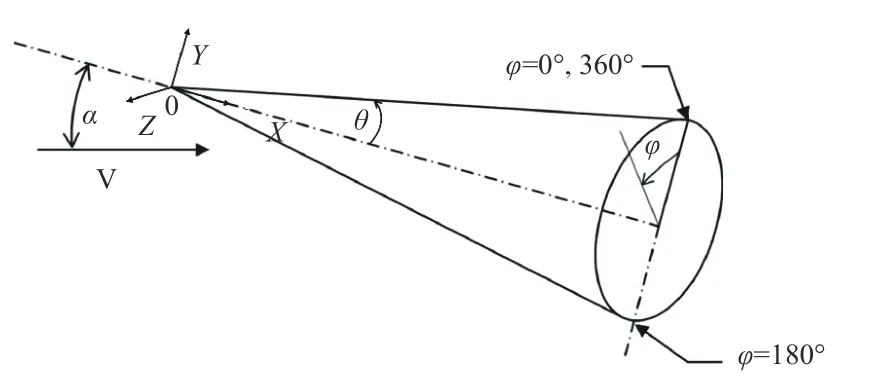
图1 圆锥几何模型示意图Fig. 1 Schematic diagram of cone geometry model

图2 圆锥计算域及网格示意图Fig. 2 Schematic diagram of cone calculation domain and grid

1.4 数值方法验证

边界层转捩前后往往伴随着表面热流以及摩阻的突跃变化，因此圆锥表面的热流或者摩阻分布可以作为转捩位置的一种表征方法. 本节基于文献[17]中的高超声速圆锥边界层转捩风洞实验的圆锥表面热流分布数据，对本文采用的γ转捩模型对圆锥边界层转捩预测能力进行验证. 在网格无关性验证中，分别对网格量为144 万的A 网格、网格量为230 万的B 网格、网格量为370 万的C 网格进行了无关性验证，其中A 网格对于试验热流值的捕捉相差较大，B 网格与C 网格对试验热流的吻合度较好. 为了在满足计算精度的同时提高计算效率，下文数值验证采用200（流向）×120（法向）×100（周向），总量约为230 万的B 网格进行计算. 计算外形和计算条件与文献[17]中风洞试验的条件下相同，圆锥头部钝度Rn=2.5 mm，半锥角θ=7°，圆锥长度L=1.2 m，自由流湍流度Tu=0.6%，湍流黏性比μt/μ=10，计算条件如表1 所示.

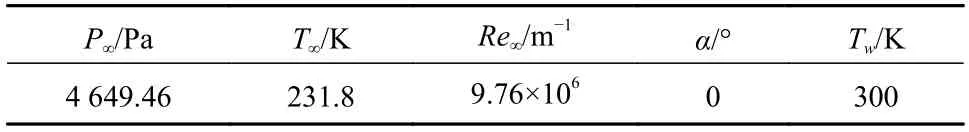
表1 算例验证计算条件Tab. 1 Calculation conditions for verification of calculation examples

本文采用基于γ转捩模型的数值模拟方法，通过计算得到了圆锥子午线上的热流分布曲线，如图3所示. 为了对比分析，图3 中也给出了分别采用Langtry和Menter 发展的γ-Reθt转捩模型、层流模型、湍流模型计算得到的结果. 由图3 可见，采用γ转捩模型计算得到的圆锥转捩起始位置和热流峰值的预测结果与实验测得的转捩位置和热流峰值基本一致，但预测得到的圆锥下游表面热流有所偏高.γ-Reθt转捩模型预测得到的峰值热流值与实验值基本吻合，对圆锥转捩起始位置的预测过于提前，这可能是由于在对经验参数标定时未对高速流进行修正. 以上结果表明，基于雷诺平均的N-S 方程，采用SSTk-ω湍流模型耦合γ转捩模型的数值方法能够比较准确的预测圆锥边界层转捩位置，适合进行对圆锥转捩位置的数值研究.

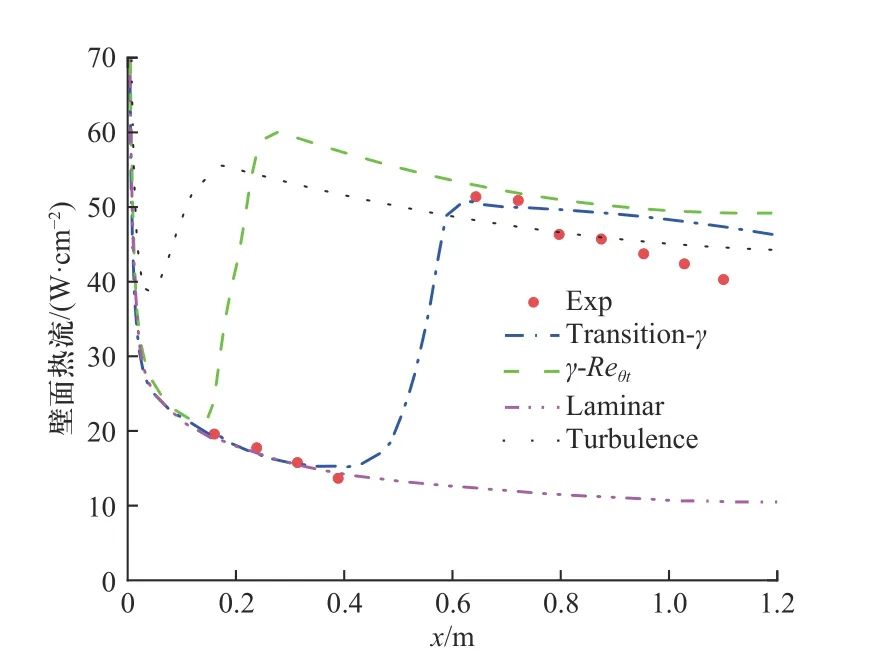
图3 圆锥子午线热流分布计算结果对比Fig. 3 Comparison of calculation results of heat flow distribution on conical meridian

2 转捩反转问题数值研究与分析

2.1 随攻角变化的转捩反转

本节采用基于耦合γ转捩模型的RANS 求解方法，对全长L=452mm，半锥角θ=8°，头部钝度半径分别为Rn=0.063 5 mm、20.32 mm 的尖锥和钝锥，在马赫数Ma=6，攻角α=0°、2°、4°、6°、8°的条件下的流场分别进行模拟计算，给出圆锥边界层转捩位置随攻角增大的变化规律，研究随攻角增大圆锥边界层转捩的反转现象. 计算条件参照文献[5]，自由流湍流度Tu=0.1%，湍流黏性比μt/μ=10，具体计算参数如表2 所示.

表2 攻角反转数值模拟计算条件Tab. 2 Numerical simulation calculation conditions of attack angle reversal

图4 给出了两种不同钝度圆锥在迎风面和背风面子午线上的转捩位置随攻角变化曲线，图中也给出了文献[5]中的风洞实验结果. 图4（a）中左侧曲线上向上的箭头表示圆锥迎风面转捩已推迟至计算外形之外，说明攻角α≥4°时圆锥迎风面边界层表现为层流状态.

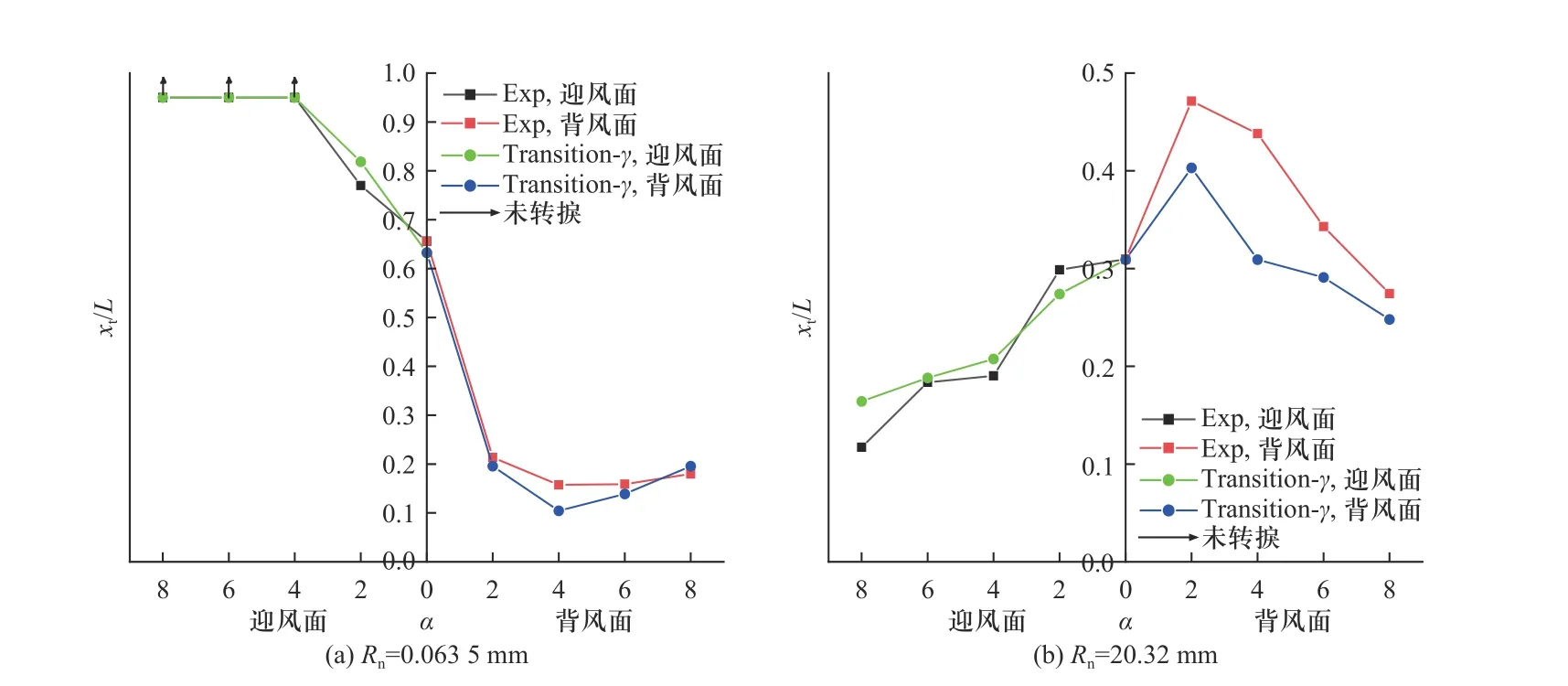
图4 圆锥迎风面和背风面对称面子午线上转捩位置随攻角变化曲线（Ma∞=6）Fig. 4 The curve of the transition position on the meridian in the symmetry plane of the windward and leeward side of the cone with the angle of attack（Ma∞=6）

由图4（a）可见，对于尖锥，当α≤θ/2 时，随着攻角增大迎风面转捩位置向后移动，背风面转捩位置向前移动且前移速随着攻角增大而减小；当α＞θ/2 时，迎风面转捩推迟至模型以外，背风面转捩位置由向前运动转变为向后运动. 在攻角不为0 时，头部钝度半径为Rn=0.0635 mm 的圆锥边界层呈现一般的非对称转捩特征. 由图4（b）可见，对于钝锥，当α≤θ/4 时，背风面转捩位置后移，当α＞θ/4 时，背风面转捩位置由后移转变为向前移动；而迎风面转捩位置则随攻角增大呈单调前移的趋势；在攻角不为零时，头部钝度半径为Rn=20.32 mm 的圆锥，迎风面的转捩位置都比背风面的转捩位置靠前，呈现转捩反转的现象，攻角α=2°时转捩反转现象最显著. 钝锥外形在背风面的转捩预测位置变化趋势与实验趋势一致，但转捩预测位置比实验值有所提前. 推测可能原因为γ转捩模型中的横流准则对于背风面横流速度较为敏感，使得转捩提前，但依然较好地预测出实验所提到的攻角转捩反转现象.

图5 和图6 分别给出了马赫数Ma∞=6，攻角α=2°时，圆锥头部钝度分别为Rn=0.063 5 mm 的尖圆锥和Rn=20.32 mm 的钝圆锥表面间歇因子分布图. 图5 和图6 中可见，有攻角情况下尖圆锥呈一般的非对称转捩特征，而钝圆锥呈现转捩反转现象，这与上面分析给出的结论一致. 图7 给出了尖锥与钝锥的周向摩阻分布曲线，从图7（a）中可知，在有攻角的条件下，尖锥表面不同子午线上的转捩位置不同且变化范围很大，背风面中心线（ϕ=0°）上的转捩位置最靠前，迎风面中心线（ϕ=180°）上的转捩位置最靠后，沿周向从背风面到迎风面转捩位置逐渐后移；在周向角ϕ从0°到90°的背风区转捩位置后移较慢，在周向角ϕ从90°到180°的迎风区转捩位置很快后移；尖锥头部附近的摩阻系数比较大，且头部迎风面的摩阻明显比背风面摩阻大；边界层转捩后表面摩阻系数显著增大，迎风面中心线和背风面中心线上转捩前后摩阻系数增大一倍以上. 从图7（b）可看出，沿周向钝锥表面转捩位置不同，迎风面中心线（ϕ=180°）上的转捩位置最靠前，背风面中心线（ϕ=0°）上的转捩位置最靠后，沿周向从迎风面到背风面转捩位置逐渐后移，出现了与图7（a）中转捩位置沿周向变化方向相反的规律，即出现了转捩反转，但钝锥表面转捩位置变化范围较尖锥的小；钝头圆锥头部的摩阻系数明显比尖锥头部的摩阻系数小，且周向分布比较均匀；与尖锥相同，边界层转捩后表面摩阻系数显著增大，但转捩前后摩阻系数的相对变化量更大，转捩后的摩阻系数约为转捩前摩阻系数的4～5 倍. 摩阻系数的突跃对应着物体壁面热流的急剧增大，因此可以判断，在处于攻角反转对应的钝锥来流条件下，迎风面的表面热防护将会是其热设计的重点.

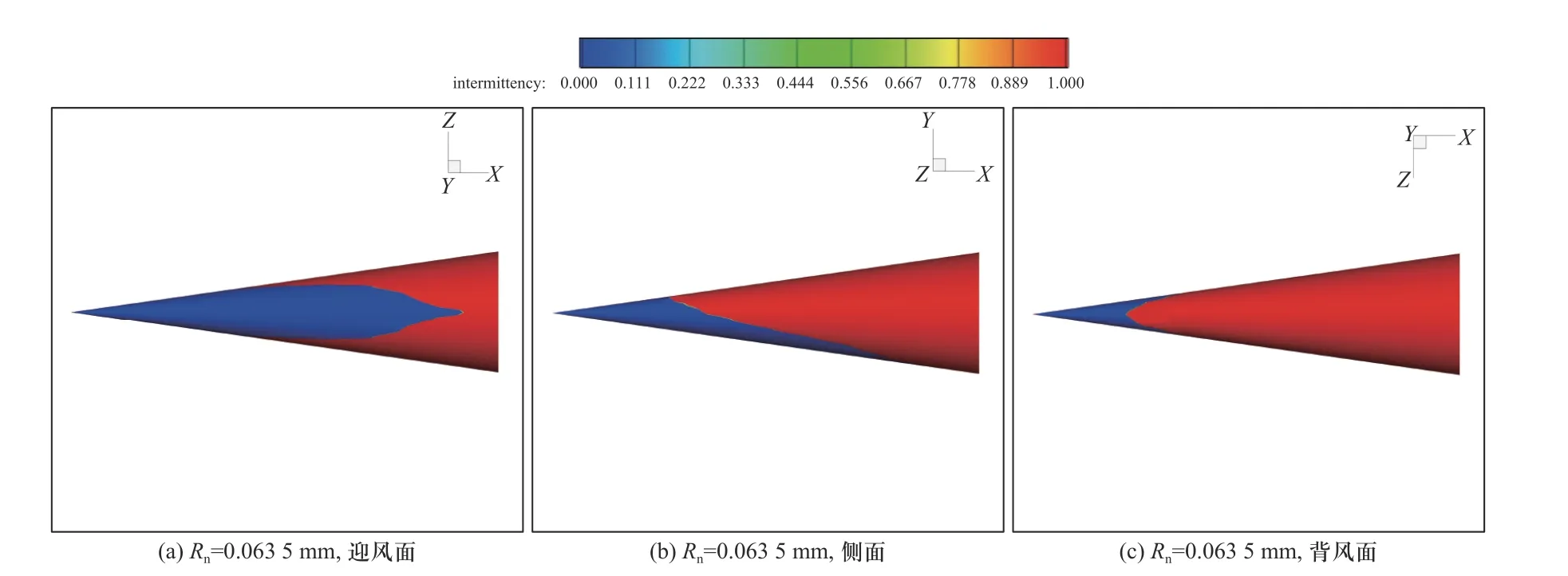
图5 尖锥表面间歇因子分布图（Ma∞=6，α=2°）Fig. 5 Distribution of intermittency on the surface of the sharp cone（Ma∞=6，α=2°）

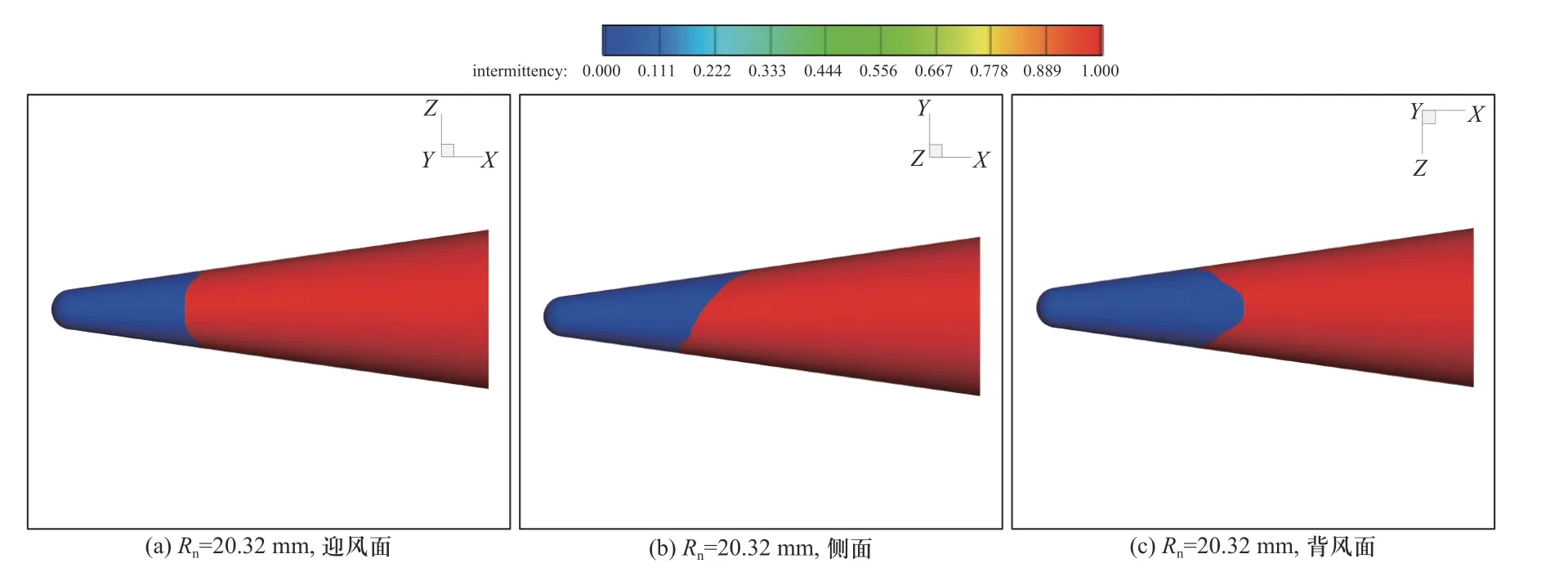
图6 钝锥表面间歇因子分布图（Ma∞=6，α=2°）Fig. 6 Distribution of intermittency on the surface of the blunt cone（Ma∞=6，α=2°）

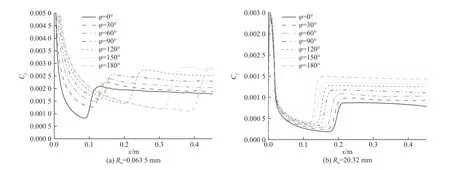
图7 不同周向角对应的圆锥表面子午线上流向摩阻系数分布图（Ma∞=6，α=2°）Fig. 7 Distribution diagram of friction coefficient of flow direction on the meridian of cone surface corresponding to different circumferential angles（Ma∞=6，α=2°）

为了进一步分析随攻角变化圆锥边界层出现的转捩反转现象，取反转现象最明显的攻角α=2°时的尖锥和钝锥流场进行分析. 沿圆锥轴向分别取x/L=0.111、x/L=0.221、x/L=0.332、x/L=0.553、x/L=0.885 的5 个轴向横截面位置. 根据图4 和图7 中的转捩预测结果，可给出不同轴向位置处尖锥和钝锥迎风面和背风面边界层内的流态，见表3. 图8 和图9 分别给出了轴向5 个不同横截面内圆锥表面的流向摩阻系数Cf和名义边界层厚度δ沿周向的分布曲线.

图8 圆锥不同横截面周向摩阻系数分布（Ma∞=6，α=2°）Fig. 8 Circumferential friction coefficient distribution of different cross-sections of cones（Ma∞=6，α=2°）

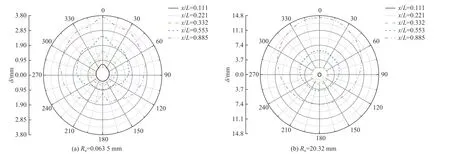
图9 圆锥不同横截面周向名义边界层厚度（Ma∞=6，α=2°）Fig. 9 Nominal circumferential boundary layer thickness of different cone cross-sections（Ma∞=6，α=2°）

表3 圆锥不同轴向位置边界层状态（Ma∞=6，α=2°）Tab. 3 The state of boundary layer at different axial positions of cone（Ma∞=6，α=2°）

从图8 可看到，钝锥和尖锥在各横截面内表面摩阻系数沿周向的分布规律不同，从摩阻系数的变化规律可看出钝锥表面的转捩呈现与尖锥不同的反转现象；结合图7 可以看到，发生转捩反转的钝锥迎风面摩阻系数明显大于背风面的摩阻系数，但总体来说钝锥表面摩阻系数小于尖锥表面的摩阻系数.

从图8（a）可见，沿轴向尖锥的流向摩阻系数的周向分布规律变化较大. 在靠近头部x/L=0.111 的横截面，尖锥周向流态为层流，此时的迎风面摩阻高于背风面摩阻，从迎风面的中心线沿周向到背风面摩阻系数一直在减小；在x/L=0.221 的横截面内，沿周向尖锥表面摩阻系数从迎风面到背风面摩阻系数逐渐减小，分布规律与x/L=0.111 横截面内摩阻系数分布规律基本一致，但摩阻系数值明显减小，此时尖锥背风面将要发生转捩，摩阻水平尚未发生突跃；当轴向从x/L=0.221 到x/L=0.332 时，可以看到尖锥背风面流向摩阻发生了突跃，这说明此时背风面已从层流发展为湍流，摩阻系数显著提高，同时可以看到在此横截面内迎风面的摩阻系数明显比背风面的小，沿周向从迎风面到背风面摩阻系数在靠近两侧最突出的位置有陡增的现象；在x/L=0.553 的横截面内，尖锥表面摩阻系数沿周向的分布与x/L=0.332 时类似，沿周向摩阻陡增处为周向转捩位置；沿流向，尖锥转捩位置逐渐向迎风面移动，在x/L=0.885 的横截面内转捩位置已移到迎风面中心线附近，除了尖锥迎风面中心线两边很小的区域外其他都已转捩为湍流流动，因此迎风面摩阻小于其它周向位置；在x/L=0.332之后的横截面内，尖锥背风面的均为湍流流动，摩阻系数值比较接近. 由图8（b）可知，钝锥表面流向摩阻分布呈现了迎风面始终高于背风面，且沿流向摩阻逐渐增大的特点；当轴向位置从x/L=0.221 到x/L=0.332时，迎风面摩阻陡增，背风面摩阻明显减小，此时迎风面边界层发生转捩，而背风面处于层流区；当轴向位置从x/L=0.332 到x/L=0.553 时，钝锥背风面摩阻陡增，此时钝锥背风面发生转捩；钝锥表面在x/L=0.885与x/L=0.553 截面的摩阻沿轴向分布规律基本一致，迎风面摩阻系数比背风面的大，该两个截面内边界均是已转捩后的湍流流动.

从图9 可以看到，在有攻角的条件下尖锥与钝锥的边界层厚度沿流向一直在增大，只是在不同的周向位置边界层厚度增大的幅度不同，导致在各横截面内呈现沿周向边界层厚度不相等的分布. 对于尖锥，其在周向各横截面内沿周向边界层厚度呈现基本相似的不对称分布规律，即背风面边界层厚度大于迎风面厚度；沿轴向从x/L=0.111 到x/L=0.221 时，图9（a）中尖锥背风面中心线附近边界层厚度陡增，此时对应背风面开始发生边界层分离；而当沿轴向从x/L=0.553 到x/L=0.885 时，尖锥迎风面中心两侧出现边界层厚度陡增的现象，这与前面分析的边界层转捩规律相同. 对于钝锥，在轴向x/L=0.111 到x/L=0.332的横截面内迎风面边界层厚度大于于背风面边界层厚度；在轴向x/L=0.553 到x/L=0.885 时，边界层厚度沿流向明显增厚，且背风面边界层厚度大于迎风面边界层厚度，圆锥在这两个截面沿周向均已发展为湍流，边界层厚度呈现的是有攻角条件下的湍流边界层特征. 沿流向钝锥最大边界层厚度从迎风到背风的这种变化规律，与其边界层转捩反转紧密相关.

2.2 随钝度变化的转捩反转

本节基于上文的数值模拟方法，对半锥角θ=7°，长度L=0.8 m 的圆锥通过改变头部钝度半径，研究头部钝度对圆锥边界层转捩的影响，头部钝度Rn变化范围为0.01 mm～20 mm，来流静温T∞=57.81 K，来流静压P∞=696.7 Pa，壁面采用等温壁面边界条件，Tw=300 K.采用与文献[8]在FD-14A 中进行高超声速钝头体边界层转捩试验相同的条件，在0°攻角下进行数值模拟计算，取自由流湍流度Tu=0.2%，湍流黏性比μt/μ=10，具体的数值模拟计算条件见表4. 表4 中也给出了由数值模拟得到的圆锥表面边界层转捩位置距头部顶点的距离xt. 表中的ReR和Re xt分别为以头部钝度、转捩位置至坐标原点距离为特征长度的雷诺数.在0°攻角下，对具有不同头部钝度的圆锥的转捩绕流场进行数值模拟，研究头部钝度对圆锥边界层转捩的影响.

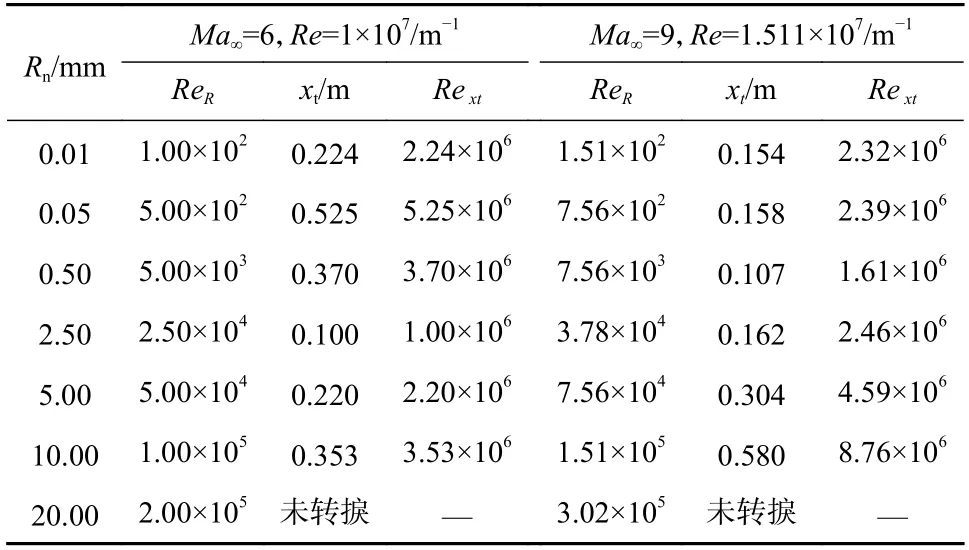
表4 不同钝度圆锥转捩计算条件及转捩数值预测结果Tab. 4 Calculation conditions for transition of cones with different bluntness and numerical prediction results of transition

图10 给出了不同头部钝度和马赫数下的转捩位置数值模拟结果和实验结果的对比，为了方便将影响转捩位置的变量进行耦合研究，横坐标为Ma2sinθ以10 为底的对数，纵坐标为转捩雷诺数Rext以10 为底的对数. 需要说明的是，因文献[8]给出的头部钝度和半锥角数据为范围量，本文所涉及的计算条件均在实验雷诺数Re和马赫数Ma范围以内，头部钝度和半锥角数值也在对应范围以内，因此图10 中给出数值计算结果时的横坐标与实验结果的横坐标并不完全一致.

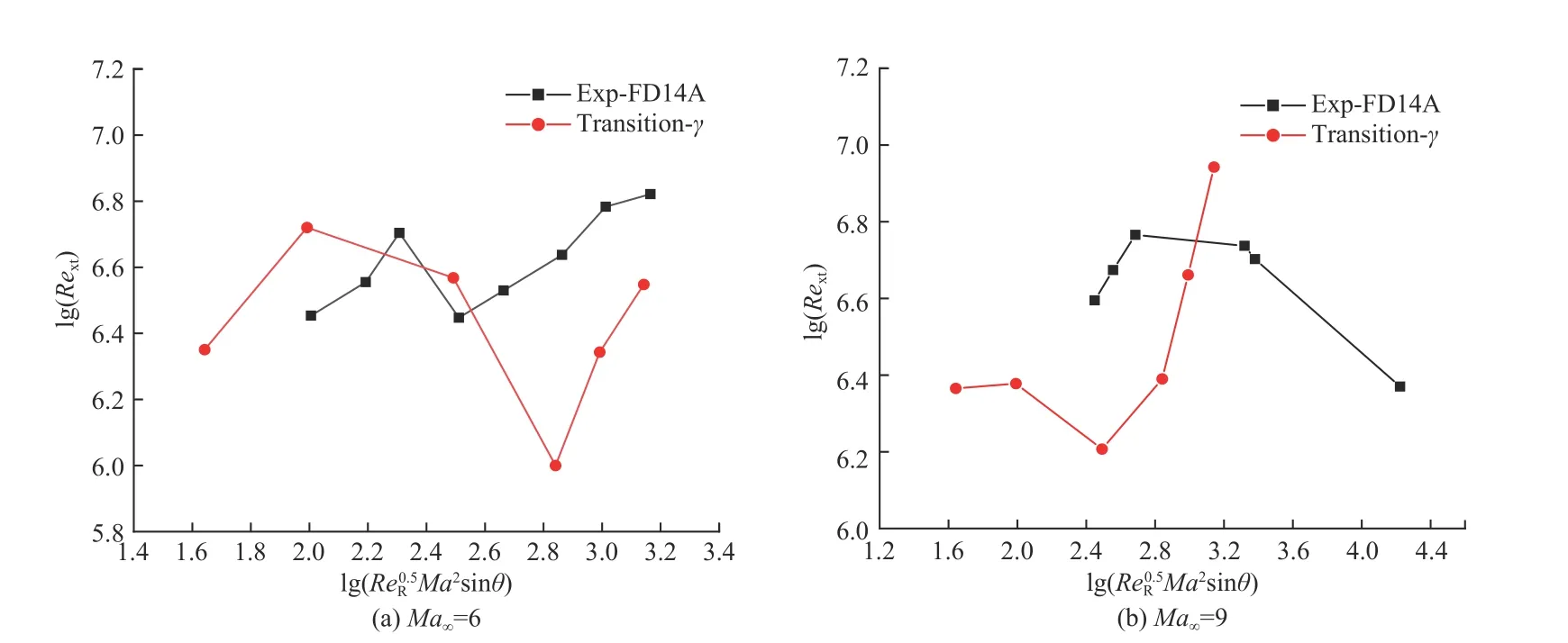
图10 不同马赫数下头部钝度雷诺数与转捩雷诺数的关系（α=0°）Fig. 10 The relationship between the head dullness Reynolds number and the transition Reynolds number under different Mach numbers

由图10（a）可知，在来流马赫数Ma∞=6，攻角α=0°时，圆锥转捩位置随着头部钝度的增大呈现了“推迟-提前-推迟”的非线性变化，即前文所述由钝度变化引起的“N”型转捩反转趋势，该趋势和实验转捩结果十分相似. 图10（b）中实验所给的转捩位置分布呈“Λ”型反转，即随着头部钝度的增大，转捩位置变化趋势呈“提前-推迟”的变化. 而在来流马赫数Ma∞=9 时，对应工况的数值模拟预测结果仍然呈现“N”型反转的分布，并且两次反转的钝度雷诺数更加接近，但计算结果中未能复现“Λ”型反转的转捩位置分布，下面针对Ma∞=6 条件下的转捩钝度反转工况作进一步分析.

图11 给出了马赫数Ma∞=6 时对应的不同头部钝度圆锥子午线摩阻系数Cf分布图. 从图11 中摩阻系数分布可看出转捩位置变化规律，在头部钝度Rn从0.01 mm 增大到0.05 mm，圆锥表面边界层转捩位置明显向下游移动，摩阻系数峰值和湍流区摩阻水平基本维持不变，层流区的摩阻系数最小值随着转捩位置的后移而减小；在头部钝度Rn从0.05 mm 增大到2.5 mm 时，圆锥转捩位置转变为向上游移动，摩阻系数峰值和湍流区摩阻水平依旧基本不变，层流区的摩阻系数最小值不断增大，并且随着钝度的增大，摩阻系数最小值的增长幅度减小；在头部钝度Rn从2.5 mm 增大到10 mm 时，转捩位置第二次向下游移动，本次移动过程中的摩阻变化特征与第一次转捩推迟相似；Rn=20 mm 时，转捩位置继续向下游移动至模型外，并且移动速度显著增快，使得圆锥表面的边界层维持在层流状态. 可见，随着圆锥头部钝度的变化，边界层转捩出现“N”型反转的过程中圆锥表面的摩阻系数的大小及陡增位置也发生了相应的变化.

图11 Ma∞=6，不同头部钝度圆锥子午线摩阻分布图（α=0°）Fig. 11 Ma∞=6, the distribution diagram of the cone meridian friction with different head bluntness（α=0°）

为了进一步从流场分析头部钝度对圆锥边界层转捩的影响规律，图12 给出了头部钝度Rn=0.01～10 mm的圆锥周围速度分布云图，图中还给出了表示熵层外缘的流线，右侧图为圆锥头部顶端附近局部放大图. 根据文献中的熵层外缘确定方法[18]，定义激波后熵变ΔS，其表达式为

取激波线上满足ΔS=0.01ΔS0的点作为熵层外缘起点，ΔS0为头部驻点熵增值. 利用激波后沿流线等熵的性质，取激波后沿熵层外缘的流线来表示熵层外缘. 从图12 可以看到，在圆锥头部钝度很小时，基于数值模拟计算得到的流场数据根据以上经验公式求得的熵层很小，因此可以近似认为在尖锥情况下不存在熵层，这一结果与文献[1]中的结论一致；随着圆锥头部钝度增大，圆锥头部激波后的熵层高度也随之基本成比例增加. 沿轴向在距圆锥头部顶点距离xn=Rn处取横截面.

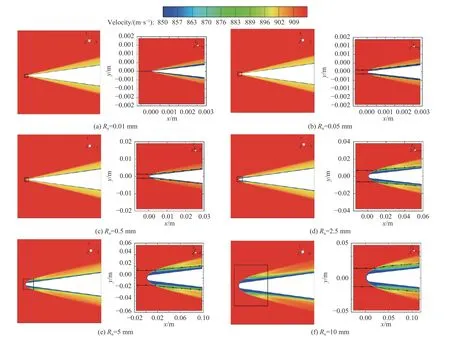
图12 Ma∞=6，不同头部钝度圆锥速度分布云图以及熵层外缘示意图（α=0°）Fig. 12 Ma∞=6, cone velocity distribution cloud diagram and schematic diagram of the outer edge of the entropy layer（α=0°）

图13 给出了该横截面内不同钝度圆锥表面的边界层厚度周向分布图，结合图12 可以看到当头部钝度相对很小时，圆锥的名义边界层厚度以及熵层高度都很小，此时圆锥头部边界层还未发展起来. 当圆锥头部钝度增大到一定值时，其头部的边界层厚度也逐渐增厚，同时头部激波后的熵层高度也随之增大，随着圆锥头部激波后熵层区域增大，熵层扰动越增强[9]，当熵层高频扰动进入边界层时，会使得边界层失稳，导致圆锥边界层转捩提前，这可能是圆锥钝度转捩反转的内在原因.

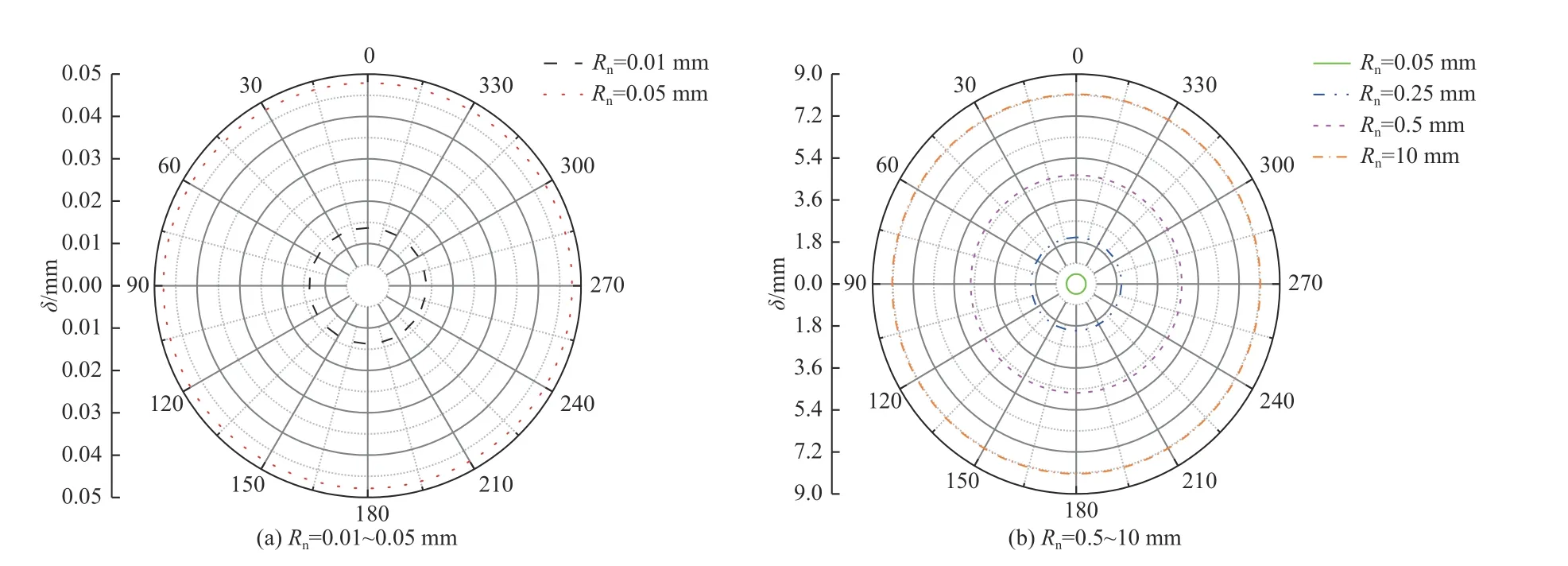
图13 不同头部钝度锥前缘名义边界层厚度周向分布图Fig. 13 Circumferential distribution of the nominal boundary layer thickness of the leading edge of cones with different head bluntness