小时间尺度网络中断故障容错识别数学建模
2022-10-25曹学勤
曹学勤,苏 荣
(内蒙古农业大学理学院,内蒙古 呼和浩特市 010018)
1 引言
小时间尺度网络指的是时间尺度极小的网络,该类网络在运行过程中,其网络流量数据具备维数较高,且呈非线性,该类网络如果发生负载,会导致链路拥塞甚至网络中断,此时链路的利用率较低。中断故障的发生会对正常网络的运用造成影响之外,会导致传输的信息造成丢失或者损坏,会给用户造成较差的使用感受,并且对于服务提供者的经济造成一定损失。因此,构建容错识别数学模型,提升该类网络承载服务的可靠性,成为当下主要手段。针对容错识别数学模型的构建,李娇等人以减少网络的拥塞、保证网络流量的均衡为出发点,提出容错识别模型;欧阳一鸣等人基于网络通信过程中的故障信息识别提出容错模型。上述方法均具备一定的容错识别能力,但是,对于网络链路的利用率不高。本文基于上述问题,为保证小时间尺度网络在发生中断过程中依据保证良好的承载服务,对小时间尺度网络传输过程中多链路发生拥塞和中断故障实行分析后,构建中断故障容错识别数学模型,保证在网络发生故障时,依据可完成数据流的传输。
2 小时间尺度网络中断故障容错识别数学建模
2.1 小时间尺度网络中断故障识别
小时间尺度网络在连接时,可通过多条瓶颈链路完成通信的往返。在任意连接中,表示输出链路,属于发送端,表示其发送效率,且为最大化;表示链路,属于瓶颈;表示有效带宽,由实行分配得出,分配对象为该连接过程;基于此,-1>则为该过程的分配满足条件,由-1、完成;表示-1、两者之间的链路,且为非瓶颈,由其向连接过程中的分配条件为≥-1。表示数量,属于瓶颈链路,且处于连接的往返过程中,其分配给该连接的有效带宽需满足>>…>条件。分组级递增量用表示,属于中断故障窗口,可用于表示速率,属于分组返回至发送端,的最大发送效率用最小值表示,该值属于和(1+)之间;>(1+)>+1则为和-1的满足条件,且位于往返路径中,此时,在该过程中的则减少条,即+1,+2,…,。
当瓶颈链路发生较长的缓冲,效率点大于中断故障窗口,此时最大分组的平均值用式(1)表示,其属于等待连接状态,为缓冲状态下,由多瓶颈链路输出

(1)
式中:=1,2,…,-1,则初始值用表示,属于中断故障窗口,且为连接状态;=。
依据式(1),以第个通信往返时间为例,两个链路分别发送背靠背个分组,均发送至瓶颈链路,属于发送端的将其发送至链路1,属于瓶颈的将其发送至链路2,此时最大分组的平均值用式(2)求解,其属于等待连接状态,为缓冲状态下
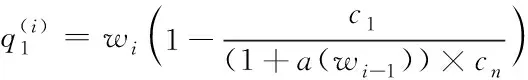
(2)
在相同状态下的最大分组计算公式为
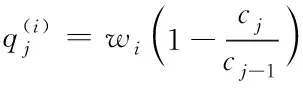
(3)


(4)
连接的有效宽带由链路分配,需满足均匀分布标准,其为
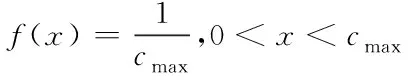
(5)
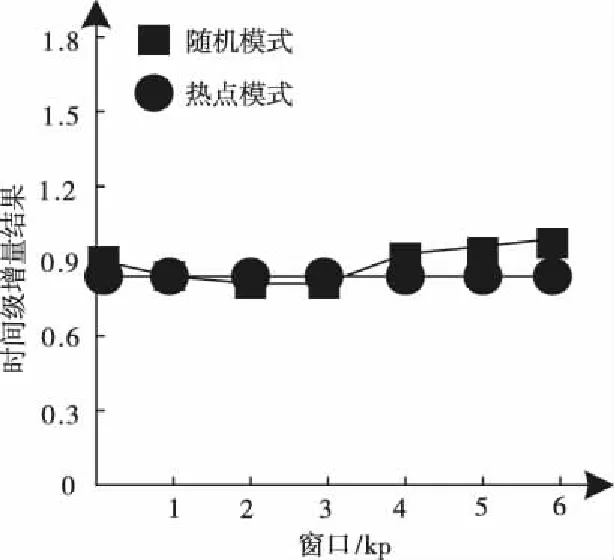
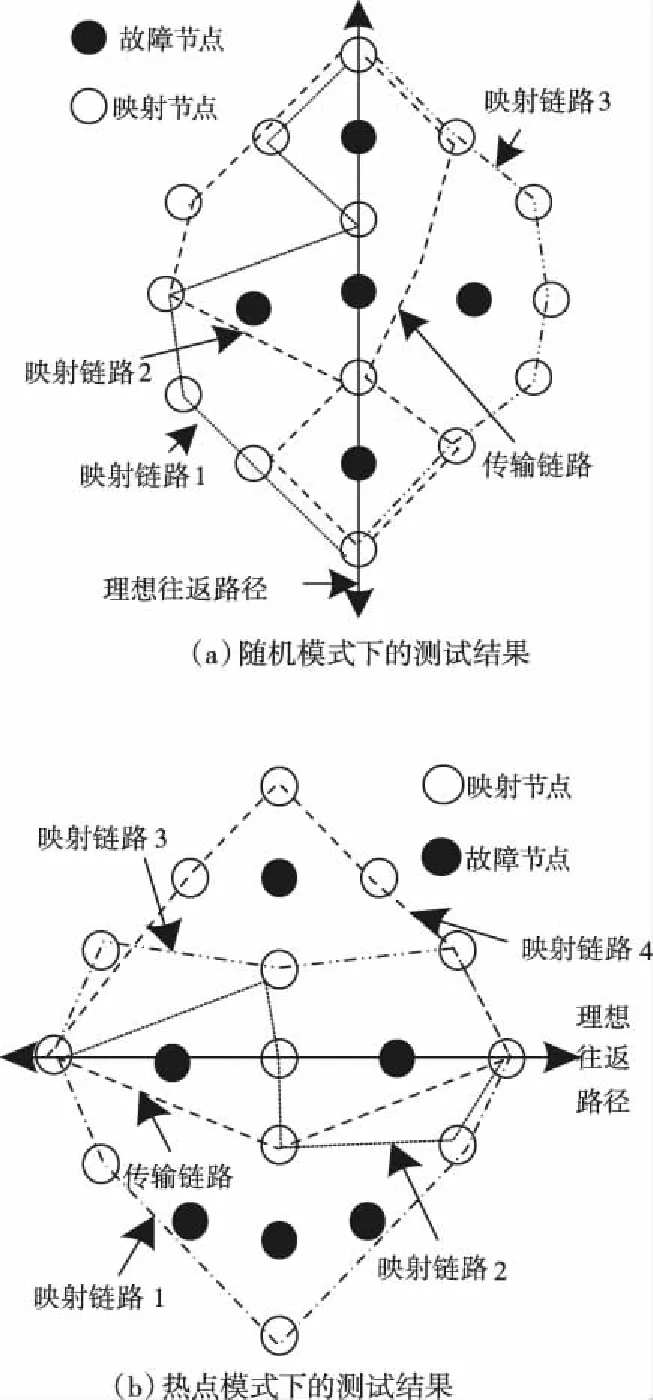
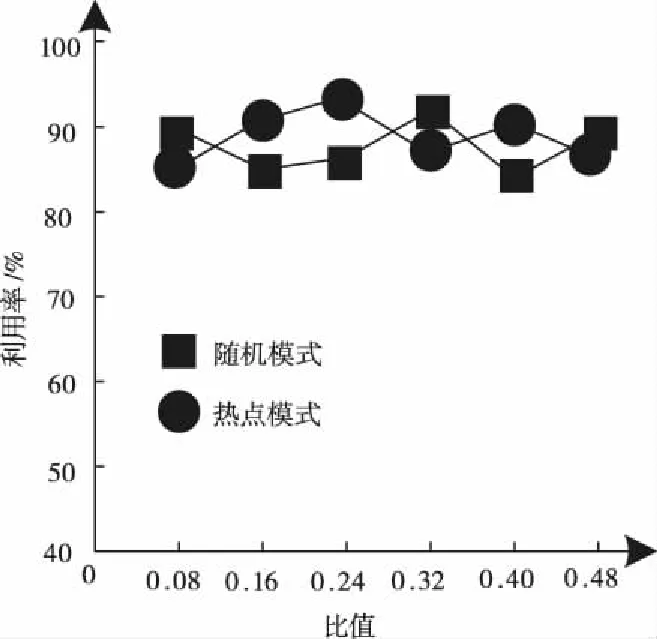
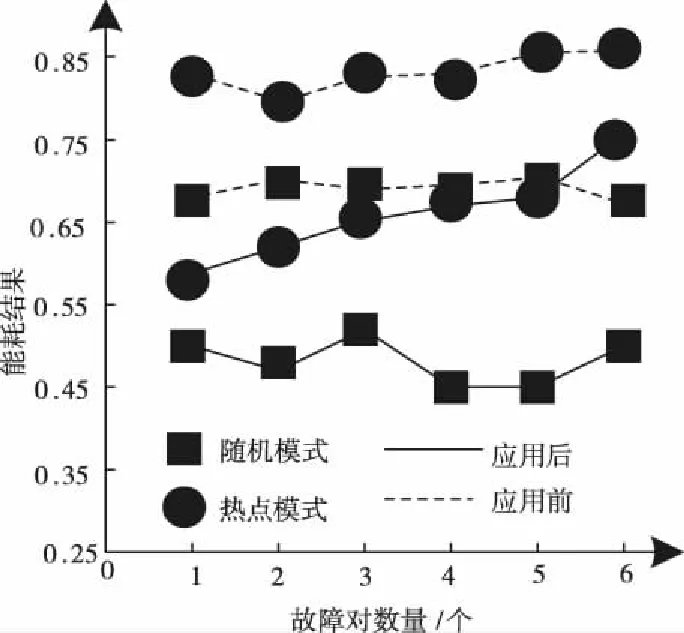
基于式(5),通信往返的路径上,数量为的链路全部成为瓶颈链路的几率低于05-1。如果=1,最小化的带宽链路一定存在于往返路径上,且为有效。如果=2,表示该路径上的有效带宽,且0<<,在其前面,一定有瓶颈链路,则< (6) 如果=,那么当=+1,+1为有效带宽,属于往返路径,且0<+1<<;在其前面的有效带宽为,…,。依据=2的结果,,…,成为瓶颈链路的可能性为05,则,,…,成为瓶颈链路的可能性为 (7) 基于2.1小节中识别的链路中断故障,构建可重构服务承载网(Reconfigurable Service Carrying Network,RSCN)链路容错数学模型,用于完成小尺度网络中断故障恢复,保证故障发生时的正常通信。 221 可重构服务承载网模型 物理网络的描述采用=(,,)无向图完成,、分别表示物理节点和链路集合,表示承载能力,其由网络提供。模型的构建标准为=(,,),其中虚节点用表示;表示集合,属于虚链路,两者是、的子集;承载力需求用表示,属于构建请求过程中。基于,可将模型的构建看作一个映射过程,用表示,该过程为至子集之间,且在满足中约束条件的基础上,其公式为 :→,=(,,) (8) 式中:⊂、⊂,服务承载能力用表示,其属于模型提供。 222 资源紧迫度 为了实现网络中资源重要程度的描述,引入资源紧迫度,其包含两个方面,即连通度和饱和度。表示节点,网络中的众多链路均由通过,因此,当发生故障后,链路会发生中断,网络将出现大面积瘫痪,将对网络的连通度造成很大影响。因此,是影响网络连通度的重要因素,因此,需考虑节点影响程度。 1)节点影响程度 设表示节点,其在中的度数用表示,影响程度向量用表示,属于和其相邻节点。 2)节点连通程度 表示资源节点,属于物理网络,其可用于描述分割程度,其是剩余网络在发生故障后引起。邻接矩阵用()表示,属于,则影响程度可用向量表示,其为=·(),属于对节点连通程度。节点连通程度随()值的增加而增加,对其实行归一化处理后,即为节点联通程度,处理公式为 ()= (9) 3)链路联通程度 链路对网络联通程度的影响强弱可通过其邻接节点影响程度实行描述,为,=(1+1)2。 4)饱和度 网络发生中断故障后,受到影响的大小可通过饱和度描述,其公式为 (10) 式中:表示资源,属于节点以及链路;()表示其饱和度;表示数量,属于,且为承载;百分比用表示,属于完成分配资源,且位于中。 5)资源紧迫程度 资源紧迫程度的获取需依据()、,、()完成,其公式为 (11) 式中:、表示调节因子,;两者之和为1。()的取值大小可表示发生中断故障后对网络造成的影响程度的大小。 RSCN链路容错数学模型的构建,衡量构建代价的同时,需保证受资故障影响的RSCN数量最小化,其通过降低对紧迫程度较高资源的占用率实现。为获取改进后RSCN链路容错数学模型的构建代价函数,需参考资源紧迫程度以及其初始价值,获取的公式为 (12) 式中:()和()均表示初始代价,前者对应物理链路,后者对应节点,均属于被RSCN链路容错数学模型占用。依据该公式可知,该模型在构建过程中,()随着资源紧迫度的增加而增加。 223 容错模型构建 对链路容错数学模型的构建需求实行分解,形成基础需求,且属于模型中任意相邻的两个节点以及连接两者的链路带宽,为(,,),也可将其看作构建模型的元需求;其中,、表示节点和需求,前者为相邻状态,后者属于链路。 模型的需求分解结束后,转变成各个元需求的依次求解;、两者之间,在中连接路径的确定,即表示模型构建,用,表示,其需满足式(12)的条件 ∀∈,,()≥ (13) 式中:带宽用()表示,属于连接链路。 由于模型构建过程中,满足元需求的候选路径数量较多,因此,选择标准为构建代价最小化。为获取、两者之间的代价最小化路径,需优化权值矩阵,为 (14) 为测试本文模型的应用性能和效果,本文采用可扩展的noxim模拟器模拟小时间尺度网络,完成仿真测试。测试时,模拟两种网络情况,分别是随机网络模式和热点模式。 测试本文方法在网络发生不同大小窗口中断故障情况下的容错效果,获取网络在两种模式的连接过程中往返时间级增量变化情况,结果如图1所示。该变化越明显,表示网络中断故障导致网络发生的缓冲越大,则容错效果较差,反之表明容错效果较好。 图1 容错效果测试结果 依据图1测试结果可知:在随机模式下,随着中断故障窗口的增加,时间级增量呈现平稳状态,没有发生波动和增加现象;在热点模式下,窗口大小的增加,时间级增量呈现小幅度上升情况,并存在较小的波动,但是整体增量级上升幅度较小,轻微波动是由于热点链接状态不稳定导致。该结果表明,本文模型具备良好的小时间尺度网络中断故障容错效果,在两种网络模式下,均可保证容错效果。 为分析本文模型的容错程度,采用长期成功运行率作为衡量标准,运行成功率越高,表示本文模型在长期中断故障下的容错程度越高。获取本文模型在两种模式下,不同的故障率和请求达到率比值结果时的长期成功运行率结果,用图2描述。期望成功运行率标准达到75%以上。 图2 长期运行成功率测试结果 依据图2测试结果可知:在不同的比值结果下,热点模式下,模型的成功运行率整体均呈现下降趋势,当利用率下降至80%左右时,则不再发生明显变化,处于相对稳定状态;随机模式下,随着比值的增加,链路的利用率发生下降趋势,但是中途呈现小幅度上升后,继续下降,利用率下降至85%左右时,趋于平稳。可满足期望标准。 为进一步测试本文模型的容错效果,模拟小尺度时间网络中不同位置节点中断故障,获取模型应用后,两种模式下网络的节点联通程度结果,用图3描述。 图3 节点联通程度测试结果 依据图3测试结果可知:当网络中部分节点发生故障后,模型可对其实行映射和并完成链路迁移,连接中断故障节点的相近和相邻节点,完成数据的通信传输,并且每个故障节点附近均保证最少两个相邻节点的映射结果。 测试文本模型应用后,在两种模式下,不同的故障率和请求达到率比值结果时,物理链路的利用率变化结果,依据该结果衡量模型构建后,网络中的资源利用的有效性,该值越高,表示资源利用率越高,系统的容错性越好,结果用图4描述。期望利用率标准达到80%以上。物理链路平均利用率计算公式为 (15) 图4 链路平均利用率测试结果 依据图4测试结果可知:比值结果的不断增加,随机模式下,链路的利用率呈现反复先下降后上升的波动变化;热点模式下,则呈现反复先上升后下降的波动变化,尽管两种模式下链路平均利用率的变化结果呈现差异化,但是利用率结果均高于80%。 为衡量网络经过本文模型容错识别后,网络在发生不同数量的中断故障时,数据包(大小为3flits)在两种模式下实行传输的平均能耗结果,以此衡量模型的应用性,结果用图5描述。其中平均能耗计算公式为 (16) 式中:静态总功耗用表示;传输过程中的整体能耗用表示;表示数据包数量,且为成功接收。 图5 数据包平均能耗测试结果 依据图5测试结果可知:本文模型应用后,随机网路模式下,随着中断故障对数量的增加,的结果呈现略微的波动变化,其结果均低于055;在热点模式下,中断故障对数量的增加,的结果呈现上升趋势,但是整体平均能耗结果均低于076。两种模式下的能耗均低于应用前,可在能耗较小的情况下,完成数据传输。 为提升小时间尺度网络容错性能,避免其发生中断故障时网络的正常传输受到影响,造成网络瘫痪,本文构建小时间尺度网络中断故障容错识别数学模型,实现中断故障容错识别,保证网络的正常通信。通过仿真测试结果表明:本文所设计模型具备良好的容错性能,可有效完成映射以及链路迁移,可在较低的能耗下完成数据包的正常传输,提升链路平均利用率。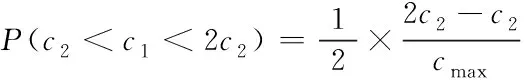
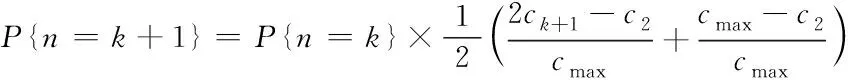
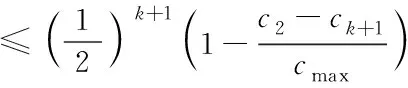
2.2 容错数学建模
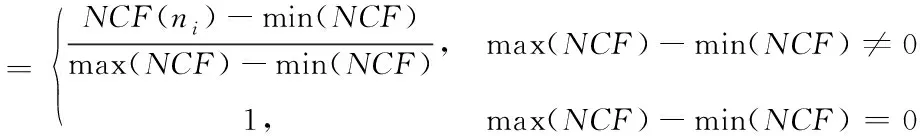

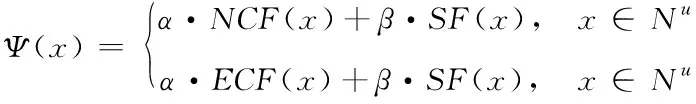
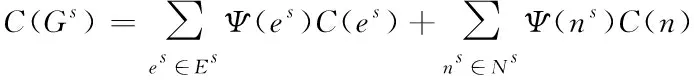

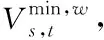
3 测试分析

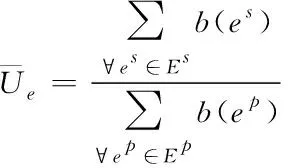
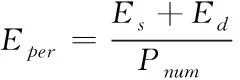
4 结论
