基于概率神经网络的增量式入侵检测方法
2022-10-25李珊珊李兆玉赖雪梅陈虹羽
李珊珊,李兆玉,赖雪梅,陈虹羽
(1. 重庆邮电大学通信与信息工程学院,重庆 400065; 2. 重庆邮电大学移动通信技术重庆市重点实验室,重庆 400065)
1 引言
随着计算机和互联网技术的快速发展,网络安全成为了一个越来越重要的问题。目前网络攻击量日益增长,攻击的类型和方式也呈现多样化趋势,因此入侵检测成为了国内外相关研究者们高度关注的焦点。入侵检测是指尽力察觉网络中的入侵行为及企图,以便采取有效的措施来保障网络安全的行为,具有入侵检测功能的系统叫做入侵检测系统[1]。
近年来,深度学习获得了越来越多的研究者的青睐,基于深度学习的入侵检测也得到了很大的发展。入侵检测中常用的深度学习模型有卷积神经网络(CNN)[2]、自组织增量神经网络(SOINN)[3]、循环神经网络(RNN)[4]、自组织映射网络(SOM)[5]、径向基函数神经网络(RBF)[6]、长短期记忆网络(LSTM)[7]等。其中,SOM和SOINN都是增量式神经网络,具有自适应、自学习、自组织的特点,可以很好地应用于实际的入侵检测中。其中,杨雅辉等[8]开发了一个基于增量式GHSOM模型的在线网络入侵检测系统,可以在线检测过程中动态更新模型,但是算法的准确率容易受到噪声影响。Han[9]等提出了一种基于前馈神经网络的增量式训练算法,较大地提升了网络的泛化性能,但是当隐单元增加时,网络收敛速度会随之减慢。还有一些将增量式学习与网络集成结合起来的入侵检测算法,如Learn++算法和负相关算法[10],但是这种网络增长的速度非常快,实用性不大。
针对上述问题,本文提出了一种基于概率神经网络的增量式入侵检测方法,在SOINN中引入了可能性理论[11],将得到的原型向量与概率神经网络(PNN)[12]结合构建PS-PNN网络,采用增量学习的方式进行入侵检测研究,在不影响之前学习结果的情况下,在检测的同时完成新内容的学习。本方法抗噪性能较强,复杂度较低,且在大数据量场景中稳定性较高。
2 相关工作
2.1 可能性理论
在实际的互联网数据流中存在着大量数据缺失和不确定的现象,具有一定的随机性,所以直接用传统方法进行评估不够严密,导致结果不精确。因此,本文考虑引入可能性理论来解决该问题。
经典集合中样本从属某个集合的概率仅取“0”或“1”,可能性理论对概率的取值扩展,将其定义为可能性隶属度,即μij∈[0,1],代表样本xj属于第i类的可能性。

(1)
ω
(2)
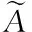

(3)
2.2 自组织增量神经网络
SOINN是一种可以对数据进行在线聚类的两层神经网络,可以输出表征数据特征的原型向量与拓扑表示。本文只使用了SOINN的第一层,并对其进行了精简,使其更加适合在线的增量式学习。
SOINN的第一步是将原始数据集输入第一层网络,生成原型向量(也就是神经元节点)来表示数据的分布。网络对原型向量的调整分为类内插入和类间插入两部分。类内节点插入的目的是减小节点的量化误差,插入的方式是在网络每经历一个学习周期后,找出当前节点中累积量化误差最大的两个点,在其中插入一个新的节点,同时更新累计量化误差值。类间节点插入的目的是生成之前没有出现过的数据模式,网络为每一个节点设置一个相似度阈值T,利用相似性度量函数(通常使用欧式距离)判断新到来的样本是否为新的模式,如果相似性度量函数值相差较大,就在样本的位置上生成一个神经元节点代表可能的新数据模式。
SOINN的拓扑结构使用竞争Hebb学习规则[13]建立,每输入一个数据样本,在特征空间中找出距离其最近的两个获胜节点,然后把它们连接起来,每条连接都通过一个参数age来记录经历的输入数据的次数。当一条边连接的两个原型向量被同时激活,将age重置归零。若age大于规定的阈值,则该连接将会被删除。
最后,SOINN通过周期性删除密度较低区域的少量节点执行去噪过程,这使得网络在噪声环境中具有较强的鲁棒性。
2.3 概率神经网络
概率神经网络(PNN)常用于模式分类,如图1所示,PNN一共包括四层,第一层是输入层,作用是接收数据点的输入;第二层是样本层,特点是神经元个数与训练样本个数相同,负责计算输入向量与中心的距离,第i类模式的第j个神经元的关系如式(4)所示
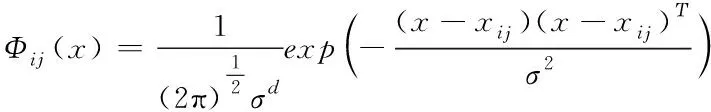
(4)
其中,xij为每个输入数据与样本之间的欧氏距离。
第三层是求和层,目的是对属于同一类别的神经元的输出做加权平均,如式(5)所示

(5)
其中,vi表示第i类别的输出,L表示第i类神经元的个数。
第四层是输出层,输出类别是求和层中值最大的一项,如式(6)所示
y=arg max(vi)
(6)
3 基于概率神经网络的增量式入侵检测方法
SOINN是一种无监督的增量式竞争学习网络,通常与有监督学习结合用于分类。本文将P-SOINN中得到的原型向量作为PNN中样本层的训练样本进行入侵检测。
3.1 P-SOINN网络
在SOINN类间节点插入的过程中,使用可能性隶属度作为新类别的判别标准来构建P-SOINN网络。假设输入数据为样本Xi,计算每个新到来的神经元节点Xi属于已有类别的可能性,寻找可能性隶属度最大的两个节点s1和s2分别作为获胜点和第二获胜点,如式(7)和式(8)所示
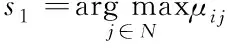
(7)
(8)
若μ(s1,i)>Ts1且μ(s2,i)>Ts2则认为Xi与已有类别的差异性过大,在Xi的位置上生成一个新的节点代表这个可能的新类别;若不满足节点插入的条件,则根据式(21)更新s1和s2的权值。
其中相似性阈值T应大于类内平均距离同时小于类间平均距离。若N为所有节点的集合,Ni为节点i的邻居节点集合且不为空,则Ti的公式如式(9)和式(10)所示
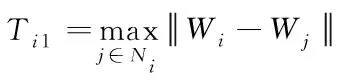
(9)
(10)
P-SOINN的目标函数如式(11)所示,计算每一个种类的类内加权平均并求和,然后求6+其最小值来计算可能性隶属度和权值的更新公式。
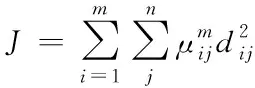
(11)
其中,m为模糊指标,根据文献[14],m取值1.5将会得到较好的效果;dij为Xi和Wj之间的欧氏距离,μij为Xi属于第j个种类的可能性,即
基于约束条件μij∈[0,1],引入一个关于μij的函数正则项f(U),当μij→0+时,在目标函数中添加一个正惩罚值使其避免出现无意义的平凡零解。采用文献[15]中选用的惩罚项
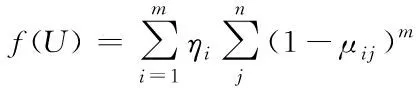
(12)
所以P-SOINN的目标函数调整为
(13)
由最速下降法可得
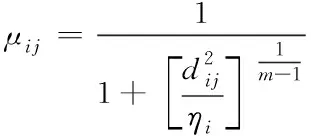
(14)
(15)
如果用上式来计算Wij,需要知道n的确切值,然而P-SOINN是一个增量学习算法,无法得到n的确切值,所以本文考虑使用一种增量法来计算。
(16)
则,Wij与W(i+1)j之间的关系为
W(i+1)j=Wij+ΔW(i+1)j
(17)
由(13)可得
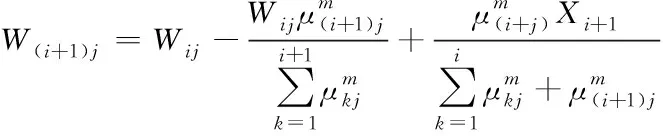
(18)
所以,ΔW(i+1)j可以用式(19)计算
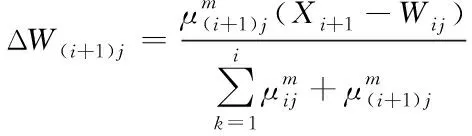
(19)
然而ΔW(i+1)j并不能用式(19)更新,因为分母中需要计算所有的输入样本Xi属于j类的可能性μij,对于增量式学习来说难度很大。本文引入加权指数进行近似计算,使得过去输入样本的权向量Wij呈指数递减。
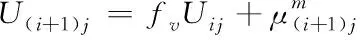
(20)
其中,fv∈[0,1],fv为加权指数,表示过去输入数据的遗忘因子,式(19)可以改写为:
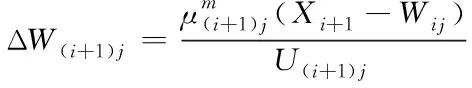
(21)
3.2 PS-PNN网络
PNN属于有监督学习,网络学习过程简单并且具有准确率高、对噪声鲁棒性好的优点,但是样本层中的训练样本需要有极高的代表性。P-SOINN得到的原型向量正好符合这个标准,将其添上标签作为PNN的样本层,对训练集进行训训练,然后对测试集进行判别。这一过程为无监督学习和有监督学习的结合。PS-PNN的总流程图如图2所示。
PS-PNN的伪代码如下所示。
算法1:PS-PNN
输入:序列点集{X},边集Ε=Φ
输出:原型向量集合{A}和测试集数据的分类结果
1)初始化点集N={c1,c2},c1和c2为最初2个数据点;
2)for{X}do
寻找N中与X最相似的两个神经元s1和s2
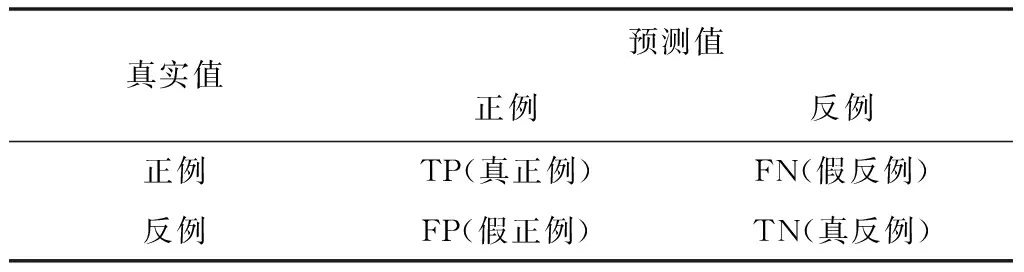
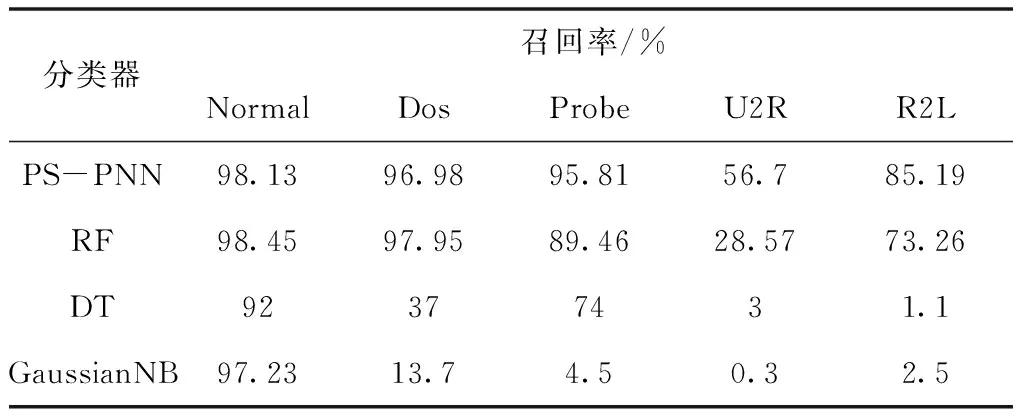
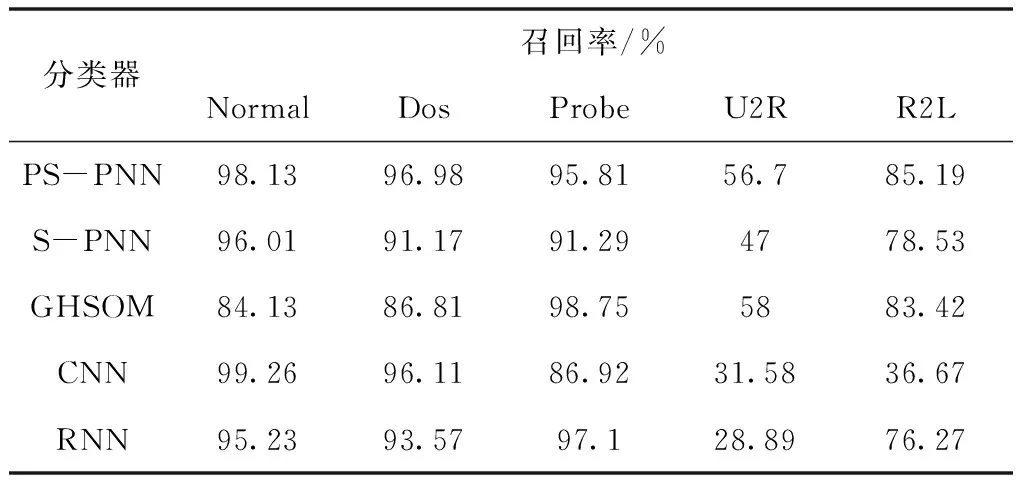
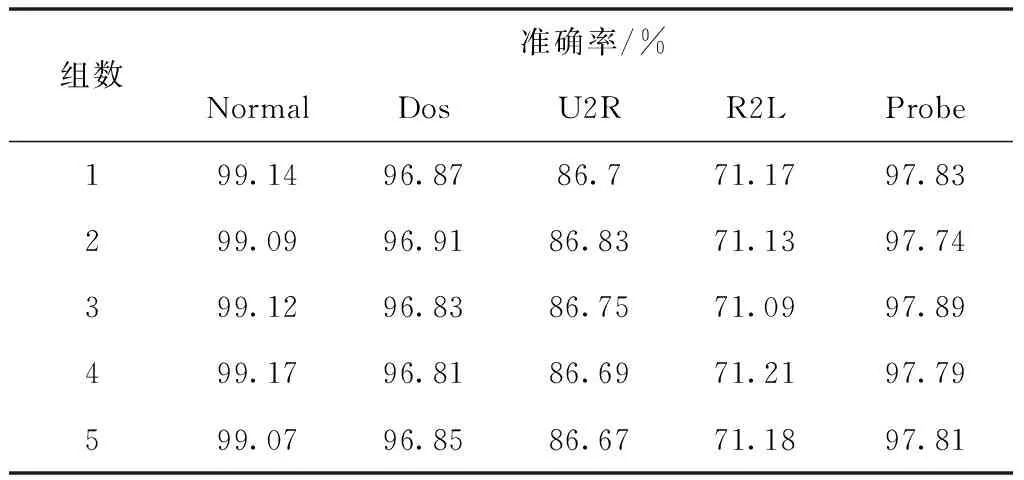
3) ifs1 thenN=N∪{X} else 更新s1和s2的权值 endif 4)ifs1和s2之间不存在连接then Ε=Ε∪{(s1,s2)} age(s1,s2)=0 endif 5)age(s1,i)=age(s1,i)+1 6)foralledgeage(i,j)>agemaxdo Ε=Ε{si,sj} 7) if 输入的数据样本量是λ的整数倍 then 执行去噪过程 end if end for 8)return 原型向量集合{A} 9)将集合{A}作为PNN的样本层训练网络 10)输入测试集数据,进行入侵检测的分类 PS-PNN网络的构建分为两个阶段,据此分别计算每个阶段的时间复杂度。 1)在P-SOINN中,当一个新的样本X输入时,需要找到获胜点s1和s2,计算X属于每一个节点的可能性隶属度,其时间复杂度是O(N)。在s1和s2没有邻居节点的情况下,最多需要再次扫描所有节点,因此时间复杂度增加到O(N2)。 2)更新所有和胜利节点s1相连的节点的权值向量Wij时,最差情况下,即所有节点都和s1相连时,时间复杂度为O(N)。 3)扫描所有节点执行噪音清除工作,时间复杂度为O(N)。 因此,P-SOINN网络处理一个输入样本的总时间复杂度如式(22)所示 Θ′=O(N2+N+N)=O(N2) (22) 4)在第二阶段的PNN中,设输入数据为M维,样本层的训练样本个数为N,在样本层进行M*N次运算,时间复杂度为O(M*N)。因此,整个网络的时间复杂度如式(23)所示 Θ=O(N2)+O(M*N) (23) 综上所述,PS-PNN网络整体的时间复杂度相对较低,适用于数据量较大的网络环境下的入侵检测。 本文使用NSL-KDD数据集进行实验,训练集中含有22种攻击类型,测试数据集中含有17种攻击类型,攻击类型主要分为四类:Dos、Probe、U2R、U2L。各类型数据在数据集中的数量和占比如表1所示。 表1 NSL-KDD数据集 数据预处理的第一步是符号型特征数值化,NSL-KDD数据集中含有41个特征,其中protocol_type、service和flag三个特征是类别特征。利用独热编码对离散数据进行处理,将字符型特征转化为数值型特征。 第二步是数值规范化,包括数据标准化和数值归一化两个部分,这一过程可以使各个特征处于相同的量级范围,对分类结果起到相同的贡献作用。 计算各属性特征的平均值,如式(24)所示 (24) 计算各属性特征的标准差,如式(25)所示 (25) 对属性特征进行标准化度量,如式(26)所示。 (26) 接下来,将标准化的结果归一化到[0,1]区间,如式(27)所示 (27) 最后,利用主成分分析(PCA)对数据特征进行降维操作,这一方法利用正交变换把由线性相关变量表示的数据转换为少数由线性无关变量表示的数据[16]。 根据入侵检测的结果,可将分类情况总结为四条:真正例,指真实值为正例且预测值为正例的数量;假正例,指真实值为反例且预测值为正例的数量;假反例,指真实值为正例且预测值为反例的数量;真反例,指真实值为反例且预测值为反例的数量。这四种情况构成了混淆矩阵,如表2所示。 表2 混淆矩阵 由混淆矩阵可以得出准确率(Accuracy)、精确率(Precision)、召回率(Recall)和F值(F-measure)四个性能指标,分别如式(28)、(29)、(30)与(31)所示 (28) (29) (30) (31) 4.4.1 参数选择分析 本文在P-SOINN算法中引入了遗忘因子,遗忘因子取值不同,分类结果会受到影响。由于遗忘因子取0.5以下时,最终的入侵检测准确率很低,所以本文的实验中遗忘因子从0.5到1取值,每隔0.02取一点,每个点进行20次实验,得到的结果如图3所示。 通过图3可以得知,当遗忘因子逐渐增大,入侵检测的四个检测标准的曲线也逐渐走高。当遗忘因子大于0.9时,入侵检测的准确率均在90%以上。图4为遗忘因子从0.9到1之间的实验结果条形图,可以更直观地看出当遗忘因子为0.99时,准确率、精确率和F值均达到最高,所以在本文的P-SOINN网络中遗忘因子取0.99。 4.4.2 实验结果分析 将预处理后的NSL-KDD数据集分别输入P-SOINN和SOINN中,实验30次后得到每个类别的原型向量的平均数量如图5所示。 由图5可见,P-SOINN的类别数量折线分布比SOINN更窄,每个类别的原型向量的数量更多,说明改进后的P-SOINN比SOINN更加稳定。训练集数据包含22种攻击类型,加上Normal类型一共23种,在P-SOINN网络中,训练集数据的原型向量被分成了23个类别,对其进行标记,用于后续的有监督学习。 将PS-PNN同随机森林(RF)、决策树(DT)和高斯朴素贝叶斯(GaussianNB)等三种常用的机器学习方法进行二分类对比实验。结果如图6所示,可以看出PS-PNN的准确率、召回率和F值均高于对比算法,证明了PS-PNN的有效性。 接下来进行五分类对比实验,本文主要对比了算法的召回率,因为召回率实际上是指检出率,可以很直观地看出每个类型的检出结果中预测正确的比例。对比结果如表3所示,可以看出与传统的机器学习算法相比,PS-PNN对U2R和R2L两种稀疏攻击类型的检出率有较大提升,说明网络对小样本攻击有强大的检测能力。其次,PS-PNN对其它三种类型的检出率也远远高于DT和GaussianNB,对于Normal和DOS的检出率仅次于RF。综合来看,PS-PNN对比另外三种算法有更大的优势。 表3 与机器学习算法的召回率对比 将PS-PNN同S-PNN、生长型分层自组织映射神经网络(GHSOM)[18]和CNN、RNN等四种神经网络方法进行二分类对比试验。其中S-PNN为SOINN和PNN网络的结合,和PS-PNN与GHSOM同为增量式神经网络,CNN和RNN为传统神经网络。结果如图7所示,可以看出增量式神经网络的准确率、精确度、召回率和F值均高于对比的两个传统神经网络算法,说明增量式神经网络用于入侵检测领域时有很大的优势。PS-PNN和S-PNN、GHSOM的对比,说明了本文将可能性理论引入SOINN中增加了网络输出原型向量的精确度,进而提升了入侵检测的准确率,从仿真结果上看,效果优于其它两个增量式神经网络。 接下来进行五种算法的五分类对比实验,每种类型的召回率如表4所示。可以看出,增量式神经网络的优势是对稀疏攻击类型的检出率有较大的提升。PS-PNN对U2R的检出率仅次于GHSOM,对R2L的检出率均高于对比算法,在其它三种类型上的检出率都具有极大的优势,证明了PS-PNN算法的有效性。 表4 与神经网络方法的召回率对比 4.4.3 网络稳定性分析 由于本网络是基于在线学习的竞争型神经网络,此类网络的结果会因为数据的输入次序改变而不同。为了验证算法的稳定性,一共进行五组实验,每组10次,得到的结果如表5所示,可以看出每组实验的准确率基本一致,虽然有微小的变化,但是在误差范围内,这表明PS-PNN受到输入次序的影响很小,验证了算法在实际入侵检测时具有较高的稳定性。 表5 分组准确率对比 本文介绍了一种基于概率神经网络的增量式入侵检测方法,通过构建增量式神经网络P-SOINN获取用于表征数据分布的原型向量,并将其作为PNN的样本层进行入侵检测。本网络可以在不影响之前学习结果的情况下,在线动态学习数据集中的新模式,且复杂度低,适用于现今互联网高速大流量场景下的入侵检测。通过相关仿真实验表明,该算法能够有效地提高入侵检测精度且总体性能优于对比算法,尤其对于稀疏攻击类型具有较高的检出率。基于此,如何对PS-PNN网络中相似性阈值进行优化选取将作为下一步主要工作。3.3 复杂度分析
4 实验与分析
4.1 实验数据集
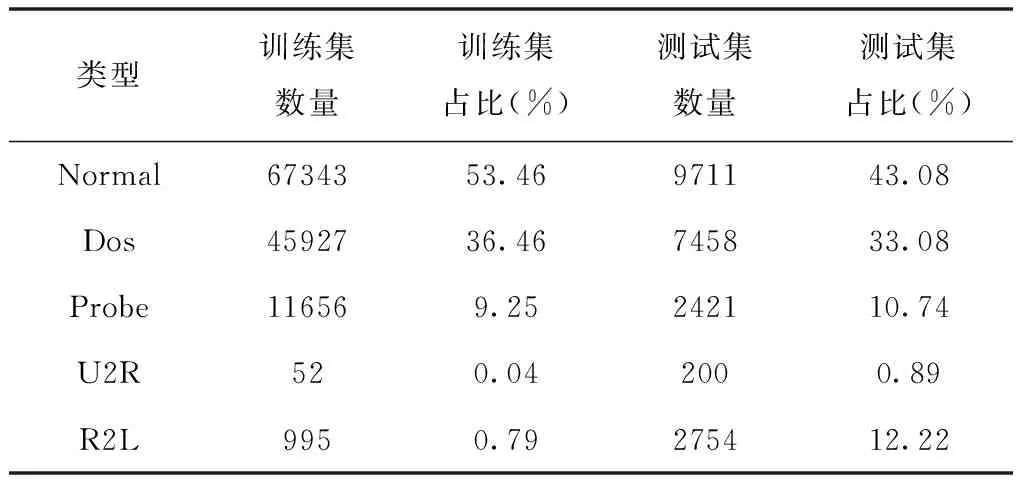
4.2 数据预处理

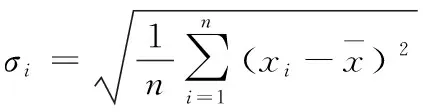

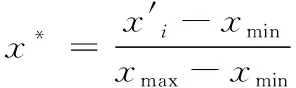
4.3 评价指标

4.4 实验分析
5 结束语
