集成局部搜索策略的PSO算法求解连续热镀锌生产调度问题研究

□ 高 聪 李百宁

一、介绍

本文研究的热镀锌机组具备以下特征使得此调度问题显著区别于其他关于热镀锌调度问题的研究：一是因为对外板有很高的表面光洁度要求，所以必须在调度前端生产外板板卷；二是任何外板都不能比其前行板卷更宽，否则会在板卷表面留下前行板卷边缘的痕迹；三是连续生产外板数有上限；四是在外板部分中，内板不能连续生产。

Okano等[27]描述了日本1家钢铁企业中的热镀锌调度问题。作者在研究中考虑了6个互相冲突的目标函数，并使用数学规划模型描述此调度问题。作者提出了1种基于3种邻域的邻域搜索算法以改进初始解。板卷之间的距离通过公式被定义，根据板卷之间的距离，可以将一些改进目标函数几率较小的移动排除在搜索范围之外，从而提高邻域搜索算法的速度。

Kapanoglu和Koc[29]在2006年研究了土耳其1家钢铁企业内的热镀锌机组调度问题。问题考虑了7种约束条件：相邻板卷在宽度、厚度、锌层厚度和退火温度上的最大跳跃；只有特定板卷可以进行宽度反跳；当需要切换表面处理类型时，需要插入至少1个非表面处理板卷；切边和内径变化不能同时进行。

Verdejo 等[28]提出了一种基于禁忌搜索的求解热镀锌调度问题的算法。所有板卷分为3类，这3类板卷之间的顺序是固定的，并且这3种板卷的排序之间没有相互关联。这篇文章研究了其中1种板卷的调度问题。作者引入了适应等级的概念来衡量相邻生产板卷之间的适应程度。

已有的关于热镀锌机组调度问题的研究，其面向的热镀锌机组均不含有本文研究对象所具有的特殊内外板约束。

粒子群优化是1995年基于模拟鱼群和鸟群在自然界中的觅食行为提出的[4]。PSO问题最初被提出是作为1种解决连续实优化问题的求解算法。当其展示出强大的广域搜索能力后，大量研究将其进行改造，以使其能够在离散解空间内求解问题[5]。杨维和李岐强[6]对粒子群优化方法进行了全面的综述。

二、问题描述

本文研究的热镀锌机组的板卷产品按表面光洁度要求主要分为2种，镀锌外板（以下简称外板）和镀锌内板（以下简称内板）。外板对表面光洁度有很高的要求，内板对表面光洁度要求一般。由于外板很高的表面光洁度要求，因此必须在调度前端生产外板板卷。原因是此时刚刚更换的轧辊表面还很光滑。很高的表面光洁度还要求任何外板都不能比其前行板卷更宽，否则会在板卷表面留下前行板卷边缘的痕迹。为了保证外板板卷的质量，当生产外板板卷时，热镀锌机组必须经常进行检查和调整。而在进行这种检查和调整时，热镀锌机组生产状况的波动又会反过来影响正在生产的板卷的质量。为了解决这个矛盾，每生产最多一定数量的外板，就需要生产1个内板。当机组生产此内板时，工程师进行机组的检查和调整。每个热镀锌的调度由2个部分组成，即内板部分和外板部分。外板部分处在调度的前部分，并且在外板部分中有内板穿插其中。在外板部分中，内板不能连续生产，即2个外板之间至多只能插入1个内板。

由于工艺技术的限制，有些板卷所要求的后处理方式不能相邻进行。当2个板卷由于后处理方式的原因，或者由于宽度、厚度、锌层厚度和退火温度中某项指标差别过大而无法相邻生产，则称这2个板卷相互不兼容。如果2个不兼容的板卷需要相邻生产，则在实际生产过程中需要在其间插入1个过渡卷。一个好的热镀锌调度，应考虑3个方面，分别是总板卷间过渡费用、插入内板费用、使用过渡卷费用。

热镀锌生产调度问题可以看作是TSP问题的一个特例，因此也是NP难问题。本文提出粒子群优化算法。为了提高粒子群算法的局部搜索能力，在基本的粒子群算法中加入了局部搜索，以强化其局部搜索能力。

三、集成局部搜索的粒子群优化方法

本研究采用Kennedy等[7]的GBEST模型。根据GBEST模型，每个粒子的移动方向都考虑其以前的最佳位置及整个粒子种群中的最佳位置。在本文中，粒子种群的初始位置和速度均随机产生。

粒子群优化方法具有较强的广域搜索能力，但其局部搜索能力偏弱。本文将局部搜索算法嵌入到粒子群算法中，以增强其局部搜索的能力。每当种群的历史最优解得到更新后，以新历史最优解为起点，进行变邻域局部搜索。

1.解的表示

粒子群算法的核心问题就是如何将1个解编码为1个粒子，并能够将1个粒子解码还原为1个解。本文研究了热镀锌机组的排序调度问题，对于此种问题，粒子群算法有比较成熟的编码方式。令N= {1, 2, 3 …, n}为所有待调度的板卷，则粒子种群中第i个粒子可以表示为，Xi={Xi1，Xi2，Xi3，…，Xin}。Xi为1个n维向量，Xip表示在该粒子中，第p个板卷所对应的数值。根据Xip的数据，Xip越小的板卷被安排在越早的位置被生产。通过改变粒子对应向量各位上的值，实现改变板卷加工顺序的目的。为区别不同迭代次数下粒子的位置，加上标t表示第t次迭代时粒子i的位置，见公式（1）：

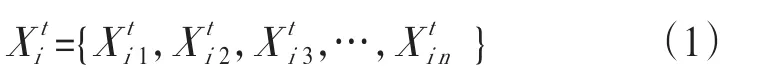
2.初始解的产生

粒子群优化方法是1种基于种群的智能优化方法，每个粒子包含速度和位置2个属性。本文中，粒子的速度和位置分别用2个n维向量表示。在算法初始阶段，随机生成各粒子的速度和位置，见公式（2）：

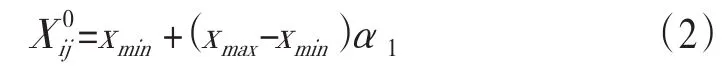
其中xmin=0，xmax=4，α1服从[0, 1]区间内的正态分布。，其中vmin=0 ，vmax=4，α2服从[0,1]区间内的正态分布。

就复分解反应而言,酸、碱、盐、氧化物之间的转化要求非常熟练,这在最新的高考考试大纲中也是“理解”的能力层次要求,从其中还可以深挖出“强酸制弱酸”“强碱制弱碱”和竞争反应等基本规律。

3.解的修复

PSO算法具有较好的广域搜索能力，但其在粒子编码空间中运动无受约束条件限制，导致根据粒子位置信息解码后的调度方案往往违反约束条件，产生不可行解，因此需对解码后的调度方案进行修复。

4.集成局部搜索的PSO算法

本节给出集成局部搜索的PSO算法的完整计算流程。

（1）步骤1：初始化

令t=0，M=2n，即待调度板卷数量的2倍。随机产生各粒子的初始位置Xi0，i=1，2，…，M；以及各粒子的初始速度Vi0，i=1，2，…，M。根据解码规则，由各粒子的位置向量解码生成其所对应的调度方案，并计算各调度方案的适应值。更新各粒子的个体历史最优值，以及种群历史最优值。

（2）步骤2：更新粒子速度和位置

令t= t+ 1。更新粒子速度，见公式（3）：

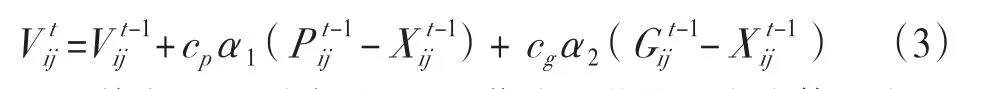
其中cp和cg为加速因子，作为调节粒子向个体历史最优和种群历史最优靠近的调节参数，α1和α2为服从[0, 1]均匀分布的随机数。

（3）步骤3：解码并更新粒子适应值

根据粒子位置向量进行解码，得到向量对应的调度方案，对不符合热镀锌工艺规程的调度方案进行修复。计算各粒子的适应值。

（4）步骤4：更新历史最优

依据各粒子的最新适应值，更新粒子个体历史最优值。依据各粒子的最新适应值，更新种群历史最优值。如果历史最优值被更新，以更新后的种群历史最优值为起点进行局部搜索，再更新历史最优值。

（5）步骤5：终止准则

如果迭代次数达到预设最大迭代次数，或连续无改进次数达到预设次数，算法终止；否则转步骤2。

5.局部邻域

本文中，为加强算法的局域搜索能力，设计了包含3种邻域的局部搜索算法。3种邻域分别为2-opt移动、路径插入移动（path insert）和路径交换移动（path swap）。为了减少计算量，当需要评价1个移动时，只计算这次移动对目标函数的增量，而不是将整个目标函数重新计算。

四、实验结果

本节介绍粒子群优化算法的实验结果。算法使用Python语言编写，并且运行在带有i5-10210 CPU和16GByte内存的个人计算机上。使用ILOG CPLEX 22.1软件作为对比基准。

1.实验数据

为了测试禁忌搜索算法，本研究随机产生了4个规模共40组算例的数据以模拟热镀锌实际生产中的情况。算例的4个规模分别为n= 20,30,50,100。对所有规模算例，板卷间的过渡费用符合[0, 150]范围内的均匀分布。参数IR用来确定哪些板卷之间是不兼容的。当产生板卷间过渡费用时，2个板卷以IR%的概率被设定为不兼容的关系。参数LO，外板最大连续生产个数，对不同规模的问题从2到4变化。在算法实验中，令α1= α2=2。具体4个规模的算例的参数设置如表1所示。因为当算例中包含的板卷较多时，CPLEX消耗的运算时间急剧增加。

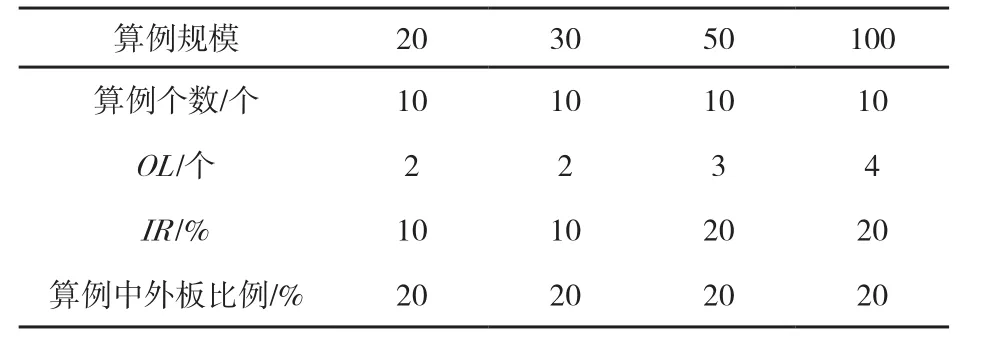
表1 实验算例配置

2.实验结果

首先对局部搜索算法的效果进行检验，以100规模的算例为对象，分别采用集成局部搜索的PSO算法和不集成局部搜索算法的PSO算法进行求解，结果如表2所示。可以看出，集成了局部搜索策略的粒子群获得的解更好。虽然消耗了更多的时间，但仍在可接受范围内。

表2 局部搜索策略效果测试

收敛过程如图1所示，可以看出，带有局部搜索的PSO算法收敛速度快于不带局部收缩的PSO算法。

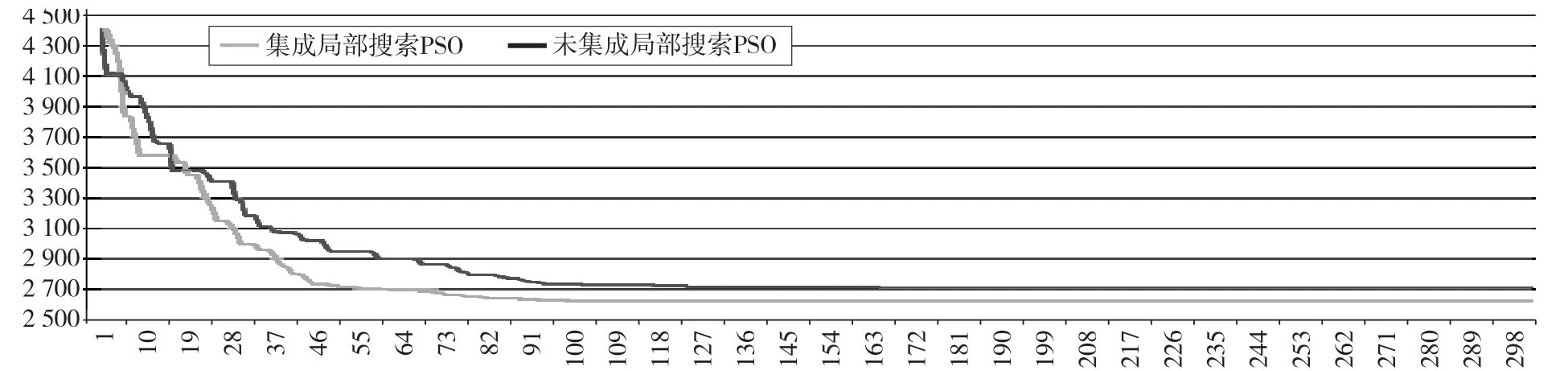
图1 局部搜索策略对收敛速度的影响

对不同规模的算例进行求解，通过与CPLEX进行对比，对集成局部搜索的PSO算法的性能进行测试，测试结果见表3。所有规模为20和30的算例，以及规模为50的10个算例中的7个算例中，CPLEX均获得最优解。对这27个算例，PSO算法也获得了同CPLEX一样的最优解。 对于另外3个算例，CPLEX没有在36 000 s内得到最优解。对这3个算例，PSO算法均获得了比CPLEX更好的解，并且这些解距离CPLEX提供的下界的平均对偶间隙小于10%。如果给CPLEX更多的计算时间，这个对偶间隙可能变得更小。对所有算例，PSO算法计算时间都比CPLEX少得多的。

表3 PSO算法同CPLEX结果比较

五、小结

本文描述了钢铁企业中的连续热镀锌生产调度问题，由于此热镀锌机组的特殊工艺要求，使得此热镀锌调度问题远区别于其他已有的关于热镀锌机组调度问题的研究。针对此问题，本文提出了用集成局部搜索的PSO算法来求解此问题；通过将PSO算法的结果同标准优化软件CPLEX的结果进行比较，认为PSO算法是有效的，并且能够在较短的时间内获得高质量的解。