盾构下穿施工变形条件下既有铁路行车限速标准研究

唐钱龙，李永恒，彭立敏，雷明锋,3

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 江西交通职业技术学院，江西 南昌 330013；3. 重载铁路工程结构教育部重点实验室，湖南 长沙 410075)

20 世纪以来，以城市轨道交通为代表的地下空间开发与利用得以深度发展，目前我国已有40多座城市开通或正在建设城市轨道交通，且大部分城市轨道交通工程采用了盾构法施工[1-2]。随之而来的是，出现了大量的盾构下穿既有运营铁路线路等近接施工工程[3]。受盾构掘进卸载的影响，地层产生沉降变形并波及至地表轨道结构，进而影响列车运行的舒适性和安全性[4]。目前，当存在盾构下穿运营铁路线路时，为保证列车运行的绝对安全，普遍性地采取45 km/h 的限速通行，但对于为何设置为45 km/h 尚无明确的理论依据，多为人为经验判断，这也直接导致线路的正常运输效率和秩序受损。因此，若能从理论上开展不同沉降变形条件下列车安全运行速度分析，建立相应的限速标准，将对保障线路运输效率和秩序起到重要的指导作用。鉴于此，广大学者针对该问题陆续开展了相关的研究工作[5-7]。PECK[8]基于实测数据，提出地层损失和宽度系数的概念，并给出了经典的PECK 经验估算公式，该公式也已广泛应用于盾构下穿施工诱发的地表沉降预测中。REILLY 等[9]收集了丰富的城市轨道交通盾构法隧道地表沉降的实测数据并开展了统计分析，建立了适用于双洞盾构施工诱发的地表沉降位移叠加法预测模型。此后，张运强等[10]在该方法的基础上，进一步研究提出了适用于不同土层条件的盾构施工三维沉降分析方法。ZHANG 等[7,11]基于列车-轨道-桥梁/隧道耦合动力学理论，提出了桥墩不均匀沉降或盾构隧道隆起时的行车安全性。蔡向辉[12]通过建立精细化大尺度耦合动力学数值模型，分析了盾构施工对列车运行时的轨道结构的响应特性。刘春阳等[13-16]分别采用数值模拟的方法，研究了盾构施工对既有轨道结构的影响，提出了盾构下穿施工对运营铁路线路影响程度的评价方法。综上分析可见，当前大部分研究都采用整体式模型或余弦型沉降曲线来模拟盾构引发的地表沉降和动力响应问题。众所周知，整体式模型涉及参数变量众多，且常常需要对盾构开挖阶段的模型进行简化，而余弦型沉降曲线忽略了幅值和波长之间的内在联系和相互影响关系，计算结果往往难以令人满意。为此，本文在既有成果的基础上，先对沉降槽曲线进行PECK公式拟合，得到不同幅值的沉降槽函数，随后建立车辆-轨道-道床耦合模型，并将不同幅值的沉降槽函数引入该耦合模型中，以分析不同沉降变形条件下的列车行车舒适性和安全性指标响应规律，进而建立相应的行车限速控制标准。

1 车辆-轨道-道床耦合模型

1.1 列车模型

根据现有铁路车辆结构特点，将车辆动力学模型进一步简化为车体(5 自由度)、转向架(5 自由度)和轮对(4 自由度)3 种模型结构及其一、二系悬挂系统，如图1。选用CRH-1 型列车作为分析对象，车辆的主要模型参数如表1所示。

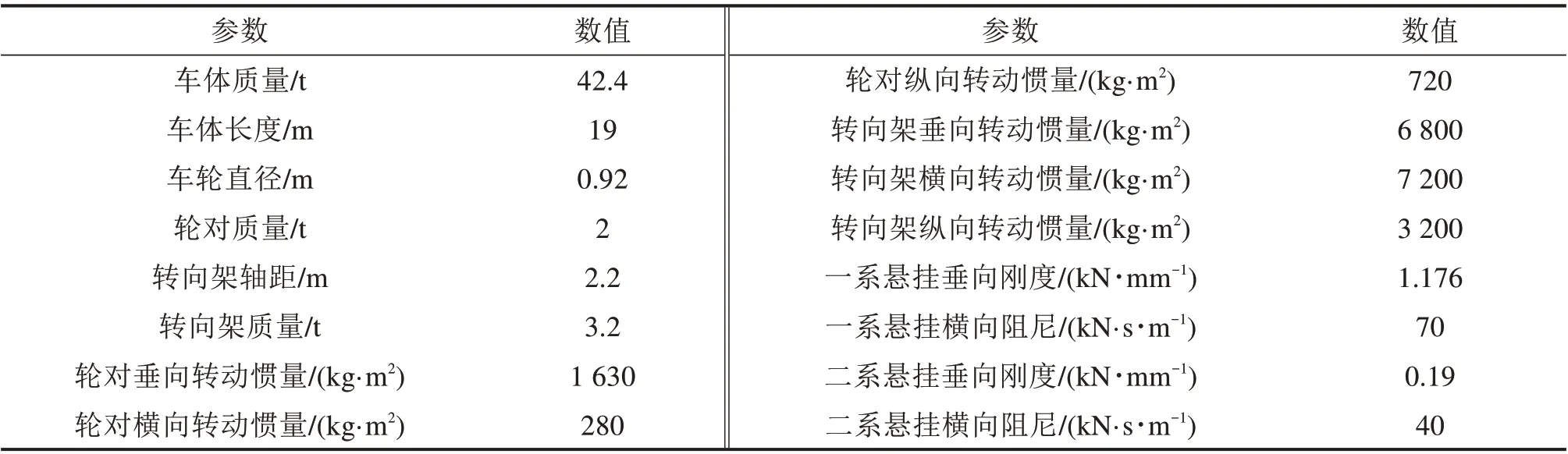
表1 车辆模型动力学参数Table 1 Dynamic parameters of vehicle model

1.2 轮-轨接触模型

在车-轨耦合模型中，由于列车处于高速运行中，车轮和钢轨之间的空间接触关系时刻发生变化，模拟过程中可将其简化为法向接触和切向接触2个部分。

1) 车轮-钢轨法向接触力

根据车轮-钢轨接触关系，可测量计算得到两者接触点的法向间隙(几何渗透量)，进而通过Hertz非线弹性接触理论求解轮轨法向接触力：

式中：P(t)为轮-轨法向接触力；Δz(t)为接触点处轮-轨间的法向间隙；G为轮-轨接触常数，取4.22×10-8m/N2/3。

在通过Abaqus 进行有限元分析时，通过Hertz接触力公式计算出P(t)与Δz(t)间的具体对应关系，随后在法向接触的自定义表格中进行参数设置标定。

2) 车轮-钢轨切向接触力

改造518刮板机驱动系统，将其输送速度从0.55 m/s提高到0.88 m/s，运输量提高到400 t/h，满足快开压滤机最快卸料速度的要求。

当轮轨与钢轨发生接触时，除了传递法向力外，还会传递切向力。切向力的大小受接触面间相对滑动速度、踏面轮缘的硬度、湿度和磨耗程度等诸多因素的影响。模型分析时，相对滑动通过设置有限滑移来进行模拟，接触面摩擦模拟采用罚函数接触模型，如图2。

1.3 道床-轨道模型

1) 整体道床及轨道模型

图3为无砟轨道动力模型，其中道床上的轨道振动采用离散弹性点支承基础上的无限长Euler 梁来模拟，通过abaqus软件中的spring弹簧模拟其在垂向、横向及扭转方向的约束。

表2 扣件单元参数Table 2 Parameters of coupler

2) 地表沉降施加模拟

既有工程实践与理论分析均表明，盾构掘进施工造成的地表沉降可用近似呈正态分布的Peck公式来描述。本文选取成都地区沉降值为5，10，15，20 和25 mm 的地表变形曲线，并通过Peck 公式在轨道板下表面施加沉降位移边界条件，模拟盾构施工导致的地表沉降变形。

1.4 模型的验证

基于上述建立的车辆模型、轨道及下部基础模型、土体模型、轮轨接触模型，通过设定接触条件和边界条件等，可进一步建立车辆-轨道-路基三维动力学耦合模型，如图4。以文献[17]案例为基础，输入相关参数，开展动力计算并提取相关结果与文献值进行对比分析，如图5。从中可以看出，采用本文建立的三维动力学耦合模型计算得到的轮轨作用力时域曲线与文献中的曲线图高度相似，模型计算得到的轮轨作用力峰值为98.53 kN，文献中道轮轨作用力峰值为99.41 kN。两者吻合较好，可见本文建立的车-轨-路基一体化模型具有可靠性。

2 行车安全及舒适性评判指标

1) 安全性标准

在车辆-轨道耦合系统分析中，常采用轮重减载率作为行车安全性的评估指标[18]。该指标未考虑轮对横向力造成的脱轨干扰，一般应用于轮对横向力几乎为0的受力工况中，具体的评判标准为：

当试验速度v≤160 km/h 时，

当试验速度v＞160 km/h 时，

2) 舒适性标准

在车辆-轨道耦合系统分析中，常选取振动加速度和平稳性指标作为评估列车运行舒适性的主要指标。上述2个指标都是振动加速度的频率和幅值来判断，但适用于不同的情况，具体为：振动加速度反应出行车过程中乘客的舒适性感知情况，而平稳性指标主要描述的是运行过程中的列车平稳度情况；本文主要针对乘客的舒适感知进行分析，故采用振动加速度指标。《高速铁路设计规范》[19]中明确指出，设计速度为250～350 km/h 的线路，列车横、竖向振动加速度均不应大于1.3 m/s2。

3 行车舒适性及安全性分析

行车安全性和舒适性主要受道床沉降变形情况和列车运行速度2类因素影响。为深入探究列车在不同道床变形和不同运行速度下的行车安全性和舒适性，建立道床最大值沉降为5，10，15，20和25 mm的5组车-轨-道床耦合模型，并分别在上述模型上进行时速为100，150，200，250 和300 km/h的列车运行模拟，分析其在不同工况下的行车安全性和舒适性。

3.1 轮重减载率

图6给出了最大沉降值为25 mm 时不同车速运行下的轮重减载率历程曲线；图7为不同沉降量下轮重减载率峰值变化曲线。

分析可知：

1) 各沉降工况下的轮重减载率历程曲线均呈现“增-减-增-减”趋势，减载率出现2 次幅度较大的震荡，第1 次震荡峰值出现在列车至65 m 位置处，此时列车驶入沉降槽的第1 个最大曲率点B附近；第2 次震荡变化出现在列车至105 m 位置处，此时列车驶入沉降槽的第2 个最大曲率点F附近；列车在最大曲率点处的行驶类似于“跳车”工况，是全过程最危险的时段。

2) 总体上，车体轮重减载率随着沉降变形程度的增加和行驶速度的提升而增大。最大轮重减载率变化范围为0.27～0.93，其中，沉降极值为10 mm 时，车速为300 km/h；沉降极值为15 mm时，车速为250 km/h；沉降极值为20 mm 时，车速为200 km/h 等工况的减载率超过了0.65 的控制标准值，对高速列车行驶造成了安全风险。

3.2 行车舒适性分析—振动加速度

同理，分别提取沉降变形前后车体中部的垂向和横向加速度及其极值变化情况，如图8和图9。值得说明的是，因列车行驶过程中，钢轨在横向未发生位移和偏转，所以横向加速度变化值较小，加速度值在0.3 m/s2，故针对竖向加速度进行分析。同时，限于篇幅仅给出地表沉降为25 mm 时的加速度历程计算结果。从以上计算结果分析可知：

1) 线路钢轨在没有发生沉降变形前，列车通过时产生的车体垂向振动加速度时程曲线较平缓，基本稳定在-0.3～0.3 m/s2之间，在驶入沉降槽区域后加速度产生波动变化。但25 个计算工况下的垂向加速度最大值为1.2 m/s2，未超过1.3 m/s2的规范控制值。可见地表沉降变形对高速行驶的列车舒适性虽构成一定影响，但其影响程度在乘客的可承受范围内。

2) 车体垂向振动加速度历程曲线变化趋势为：列车行驶在沉降槽的“下坡”开始段，对应里程为50～65 m，垂向加速度均值降为负，出现负向峰值；列车行驶在沉降槽的“下坡”稳定段，对应里程为65～90 m，垂向加速度均值开始由负变正，并出现正向峰值；列车行驶在沉降槽“上坡”开始段，对应里程为90～110 m，车辆垂向加速度开始由正回归到0。表现为先失重后超重的变化过程。

3) 列车行驶速度在0～250 km/h 时，行车速度对列车竖向加速度影响显著，运行速度每提高50 km/h，加速度增幅为20%～45%；地表沉降较小时，对列车竖向加速度影响不大，但当Peck 沉降槽深度超过20 mm 时，车体加速度增幅显著提升，每增加5 mm加速度值提升可达50%～84%。

3.3 行车限速控制标准

综合上述可知，仅从0～25 mm 的Peck 形态沉降曲线角度，列车在300 km/h 的行驶速度以内，除极个别瞬间会出现行车舒适性问题，大多数情况受轮重减载率控制，即当沉降超过一定值且行车速度高于某个范围时，轮重减载率将超过0.65，对行车安全造成风险。为此，可将轮重减载率0.65作为控制值，绘制沉降值与行车速度的对应曲线，如图10，从而可确定线路不同沉降时对应的安全行车速度区间。

进一步，为方便实际应用，以25 km/h 为间隔，划定不同沉降量时对应的安全行车速度控制表，如表3。值得说明的是，表3 所给定的安全行车区间仅仅是从轮轨减载率角度划定的，未考虑管理水平、线路的既有不平顺性以及管理安全系数等，实际应用过程中，可结合上述因素，按照一定的安全系数确定。

表3 行车限速标准Table 3 Standard table of driving speed limit

4 结论

1) 基于Herze 非线弹性接触理论，考虑车辆、轨道、道床和盾构引发的变形之间的相互作用关系，建立了车-轨-道床动力耦合模型，可快速对不同沉降条件下行车安全性和舒适性进行模拟计算。

2) 以Peck 沉降特征曲线为基础，分别分析了最大沉降值为0～25 mm时，列车以100～300 km/h的行驶速度(共计25个工况)通过沉降区线路时的安全性和舒适性指标变化规律。结果表明：列车轮重减载率和竖向加速度随Peck 沉降槽深度和行车速度的增大而增加；列车通过沉降区段时，轮重减载率为控制性指标，即当沉降超过一定值且行车速度高于某个范围时，轮重减载率将超过0.65，对行车安全造成风险。

3) 基于轮重减载率的安全性评价指标，并考虑实际工程应用，以25 km/h 为间隔，划定了不同沉降量对应的安全行车速度控制标准，为盾构下穿既有运营铁路路基管控运行时限速标准的制定提供直接依据。需要说明的是，上述限速标准的制定未考虑管理水平和管理安全系数等因素。