轨道车辆零碳感知压电俘能工程建模及分析

丁亚琦，彭乐乐，李晓靖，周炯，郑树彬，张园

(1. 上海地铁维护保障有限公司 车辆分公司，上海 200031；2. 上海工程技术大学 城市轨道交通学院，上海 201620)

轨道车辆零碳感知兼顾绿色环保及轨道车辆状态数据感知互联，其技术的发展有助于碳达峰及碳中和目标的实现，推进交通强国战略中数据资源赋能交通的发展。利用压电发电实现轨道车辆状态感知传感器自驱化是轨道车辆零碳感知的核心技术[1-3]。压电俘能结构建模及发电特性分析[4]是实现轨道车辆传感设备能源自供给的理论基础。压电俘能器通常采用压电悬臂梁结构[5-7]，该结构一端固定，一端自由运动[8-9]，一般主要是由压电陶瓷、金属基底和质量块组成[10-11]，压电陶瓷受外界作用力下发生形变，从而引起正压电效应产生电荷。然而，受轮轨作用力及线路不平顺的影响，轨道车辆走行部处的瞬间冲击高达100 g 以上[12]，常规悬臂梁式压电俘能结构通常应用在1 g 以下[3]，造成压电陶瓷碎裂而较难满足轨道车辆走行部处微传感器供电需求。针对压电悬臂梁建模及发电特性分析上，以往的建模方法通常是基于压电梁结构及力学特征，建立其分布参数机电耦合模型[13-17]，这会导致模型公式复杂、参数繁多，不利于模型求解和工程化应用。思建行等[13]通过分析压电梁机电耦合特性并利用模态分析法构建了双晶片压电悬臂梁双向耦合分布参数模型。郭抗抗等[14]在考虑压电材料非线性特性基础上，建立了单晶压电悬臂梁机电耦合模型，获得了压电材料非线性、外激励参数及负载电阻对发电功率的影响规律。孙舒等[17]针对双稳态压电悬臂梁发电系统，建立了集中参数模型并得到了其悬臂梁发电系统的特性。因此，目前轨道车辆零碳技术中，压电俘能发电难点在于缺少适应轨道车辆振动强烈且瞬间冲击大的俘能结构和统一的工程化建模方法，难以达到与车辆振动频率适配及功率最大化发电的目的。针对该问题，本文采用一种新型压电俘能结构，并针对该结构提出一种统一的工程化建模方法，实现了发电特性工程化分析，可为轨道车辆零碳感知技术推广与应用提供理论基础。

1 轨道车辆零碳感知压电俘能工程建模

轨道车辆零碳感知压电俘能结构工程建模是实现轨道车辆走行部件健康状态零碳排放感知及数据互联互通的传感设备能源自供给的理论基础。图1给出了轨道车辆零碳感知压电俘能工程建模方案。首先，基于欧拉-伯努利梁理论建立双端固支式压电悬臂梁本构模型，推导出压电俘能结构谐振频率与结构参数关系，可为频率适配提供理论基础。其次，对非线性车辆振动状态下压电俘能结构进行受力分析，获取压电结构机电耦合等效模型，得到输出功率与加速度及结构参数方程，并通过构建无量纲工程化模型简化方程的复杂程度，可实现发电特性工程化分析及应用。

1.1 压电俘能结构及本构模型

为了适应轨道车辆振动强烈且瞬间冲击较大的实际应用环境[18-20]，采用新型双端固支式压电梁结构，该结构由金属基底、压电陶瓷及质量块组成，如图2所示。压电陶瓷粘贴于金属基底的上下表面组成压电双晶片，质量块通过螺栓固定于双晶片上下压电陶瓷表面中央处，双晶片两端固定。当压电梁受到外界振动时，质量块由于惯性作用使双晶片发生机械形变，从而将机械能转换为电能。

以压电双晶片几何重心作为原点，建立XYZ坐标系，如图3 所示。设压电双晶片长度为Lpcb，宽度为Wpcb，压电陶瓷厚度为tpm，金属基底厚度为tssm，质量块长度为Lm，高度为tm，质量块与压电陶瓷等宽。

基于欧拉-伯努利梁理论可得到压电双晶片的单位宽度挠曲模量Dp为：

式中：Essm为金属基底杨氏模量；Epm为压电陶瓷杨氏模量。设压电陶瓷密度为ρpm，金属基底密度为ρssm，单位长度的压电梁的质量m为：

双端固支式压电梁质量ms为质量块质量Δm与压电双晶片质量me之和，其表达式为：

式中：a(x)为压电双晶片上某一点沿Z轴的轴向加速度；a(Lpcb)为压电双晶片中点沿Z轴的轴向加速度。利用欧拉-伯努利梁理论可得双端固支式压电梁结构的谐振频率fr为：

式中：ks=3DpWpcb/为压电双晶片等效弹性模量；为n阶模态特征值。由式(3)和式(4)可得到压电梁谐振频率fr与结构参数关系为：

1.2 无量纲工程化建模

在轨道车辆运行过程中，压电梁主要受到轮轨垂向加速度及冲击作用下质量块惯性力和因压电梁响应加速度与固定支点激励加速度不同而产生的相对作用力。将质量块惯性力等效为F(t)，支点相对作用力产生的位移为y(t)，压电梁等效为刚度为ks，阻尼系数为bt的弹簧阻尼系统的等效机械模型和电流源与压电等效夹持电容Cp并联的等效电路模型，则压电结构机电耦合等效模型如图4所示。

由材料力学可知，压电陶瓷相对平衡位置的位移z(t)为：

当轨道车辆振动时，设固定支点的激励加速度为ÿ(t)，则压电陶瓷动力学方程可以表达为：

式中：α为压电等效力压转换因子；Vp为压电输出电压。由基尔霍夫定律可列出压电梁KCL方程：

式中：Rp为纯电阻负载。对式(8)进行拉普拉斯变换可以得到Vp为：

对式(7)和式(8)进行零初始条件下的拉普拉斯变换并化简，得到压电梁相对运动位移z(t)与固定支点激励加速度ÿ之间的传递函数关系：

由图4中压电结构等效电路可知，输出功率等于消耗在负载Rp上的电功率，压电结构输出功率PH可表达为：

将式(9)代入式(11)可得：

将式(10)代入式(12)，可得输出功率与激励加速度及结构参数方程：

由式(13)可以得出，轨道车辆零碳感知双端固支式压电梁输出功率受等效质量ms，激励加速度yM，压电等效力压转换因子α，系统等效阻尼系数bt，系统等效刚度ks，负载Rp和压电等效夹持电容Cp7个物理量的影响，且参数间相互耦合。轨道车辆在运行的过程中，压电梁受到复杂的外界非线性振动激励，使得难以分析压电结构发电特性，不利于结构参数设计与工程化应用。为了工程化模型，将式(13)中参数进行无量纲化。

基于“物理相似”、“运动相似”和“动力相似”的数据无量纲化准则[21]，利用比值法和曲线形标准化函数法，将式(13)中的7 个参量映射为4 个无量纲参量，如表1所示。

表1 模型无量化参数映射表Table 1 Parameters mapping table of the dimensionless model

利用表1 中的无量纲参数对式(13)进行无量纲化，再对输出功率PH进行归一化处理，以获取无量纲统一模型，设参考输出功率为：

则归一化输出功率PˉH表达式为：

将表1 中无量纲参数代入式(15)得到无量纲压电俘能工程化模型：

将式(16)与式(13)相比，模型由7 个参量降至4个无量纲参量，简化了模型计算复杂程度，有利于发电特性工程化分析。

2 模型验证及发电特性分析

为了验证轨道车辆零碳感知压电俘能无量纲工程化建模方法的正确性，利用COMSOL 有限元软件构建了双端固支式压电梁仿真模型，如图5所示。模型主要由金属基底、上下压电陶瓷片及质量块组成，其关键参数如表2所示，仿真模型采用自由四面体网格划分方式。对上海地铁5号线阿尔斯通车辆的轴箱处振动加速度进行采集，采样频率为5 kHz，测试区间为剑川路测试线，通过傅里叶变换分析获取轨道车辆振动加速度一阶主频率为83 Hz。因此，仿真设定激励加速度频率范围为82～84 Hz 之间的正弦信号，以步长为0.2 Hz 进行扫频。

图6为搭建的实验平台，主要由主机、信号发生器、功率放大器、激振器、压电陶瓷、转换电路、控制软件和示波器组成，采用与仿真模型相同的参数及激励大小。利用绝对偏差AE、最大绝对偏差MAE和相对偏差百分比E来评价模型的精度：

式中：i表示第i个点数；Vri为给定值；Vci为计算值。

将表2 中的参数代入式(5)和式(16)可以获得压电俘能结构的理论谐振频率及输出功率，利用输出功率P与输出峰值电压Vp的关系，如式(19)，可以由实测输出峰值电压计算出实验输出功率。

表2 仿真及工程模型关键参数Table 2 Key parameters setting of simulation and engineering models

图7 和图8 分别为双端固支式压电梁在激励频率从82 Hz 到84 Hz 时的输出功率对比图和输出峰值电压对比图。从图7 和图8 可以看出，理论值与仿真值以及实测值，无论是在输出功率方面还是在输出峰值电压方面，变化趋势基本一致且数值非常相近，同时均呈现出在一阶谐振频率83 Hz时，输出功率和峰值电压达到最大值，验证了本构模型与无量纲工程化建模的正确性。

图9和图10分别对应频率从82 Hz到84 Hz时，输出功率绝对偏差和峰值电压绝对偏差对比曲线。表3 为频率从82 Hz 到84 Hz 之间的输出功率及峰值电压统计结果。从图9、图10 和表3 中可以看出，理论值与仿真值之间的输出功率绝对偏差和绝对峰值电压偏差均较小，最大偏差为82.8 Hz时，其对应的理论输出功率P为1.446 mW，理论峰值电压Vp为5.378 V；仿真输出功率P为1.482 mW，仿真峰值电压Vp为5.445 V。对应的最大绝对功率偏差MAEP为0.036 mW，功率相对偏差百分比EP为2.501%；最大绝对峰值电压偏差MAEVP为0.067 V，峰值电压相对偏差百分比EVP为1.243%。同理，从图9～图10 和表3 中还可以看出，理论值与实测值之间的输出功率绝对偏差和绝对峰值电压偏差均较小，最大偏差为82.4 Hz 加速度时，其对应的理论输出功率P为1.383 mW，理论峰值电压Vp为5.259 V；实测输出功率P为1.412 mW，仿真峰值电压Vp为5.197 V。对应的最大绝对功率偏差MAEP为0.029 mW，功率相对偏差百分比EP为2.154%；最大绝对峰值电压偏差MAEVP为0.055 V，峰值电压相对偏差百分比EVP为1.035%。

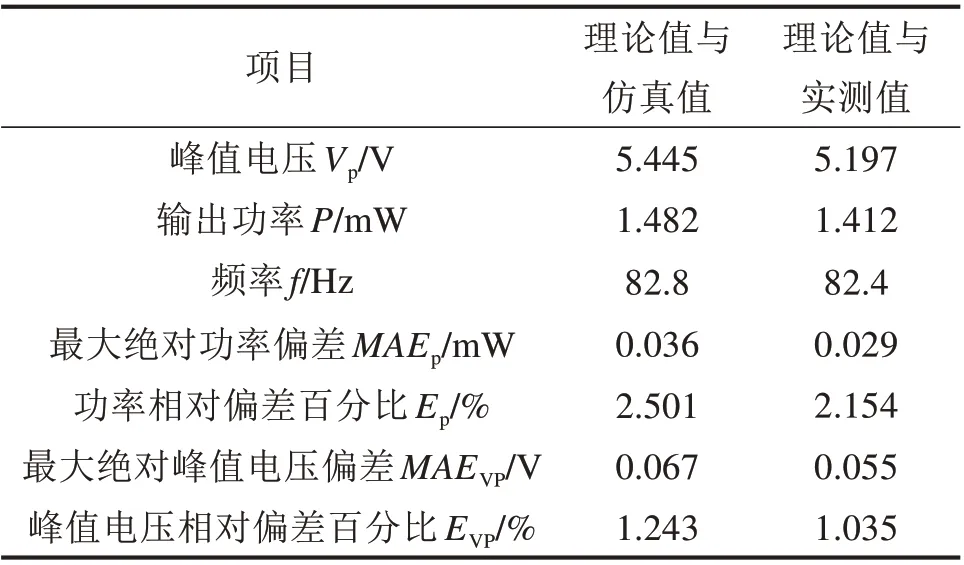
表3 82～84 Hz下输出功率及峰值电压结果统计Table 3 Statistical results of output power and peak voltage from 82 to 84 Hz

为了进一步分析压电俘能结构在一阶谐振频率下模型精度，表4 给出了在83 Hz 下理论值、仿真值与实测值所对应的输出功率及峰值电压的统计结果。从表4 可以看出，在1 阶谐振频率下理论输出功率P为1.465 mW，理论峰值电压Vp为5.412 V；仿真输出功率P为1.500 mW，仿真峰值电压Vp为5.477 V；实测输出功率P为1.484 mW，实测峰值电压Vp为5.447 V。对应的仿真最大绝对功率偏差MAEP为0.035 mW，功率相对偏差百分比EP为2.390%；仿真最大绝对峰值电压偏差MAEVP为0.065 V，峰值电压相对偏差百分比EVP为1.201%。同理，对应的实测最大绝对功率偏差MAEP为0.019 mW，功率相对偏差百分比EP为1.297%；仿真最大绝对峰值电压偏差MAEVP为0.035 V，峰值电压相对偏差百分比EVP为0.647%。对比仿真数据和实测数据可以得出，理论值在1阶谐振频率下，建立的无量纲工程化模型的计算值更加靠近实测值。

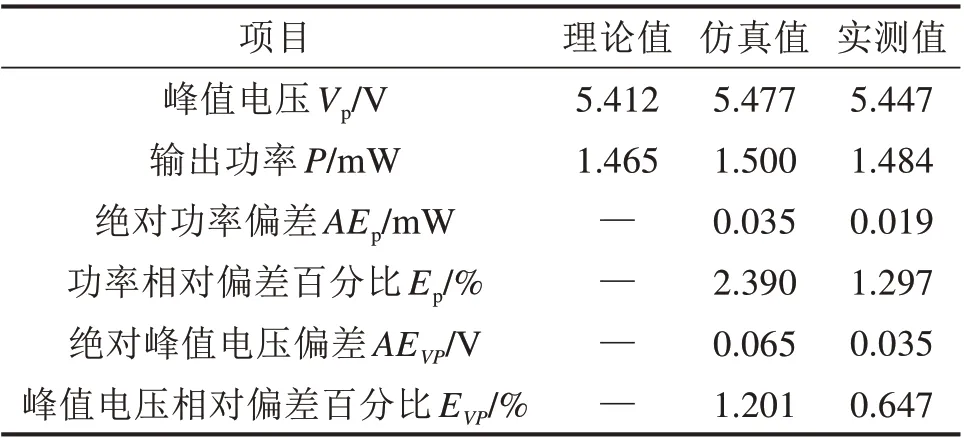
表4 1阶谐振频率83 Hz时输出功率及峰值电压结果统计Table 4 Statistical results of output power and peak voltage for resonance frequency 83 Hz

综上所述，无量纲工程模型无论是在1阶谐振频率附近还是1 阶谐振频率点处，其精度均在3%以内，且理论计算值均比仿真值更加接近实测数值，这说明本文所建立的模型不仅在保障精度的前提下实现了模型简化，而且更能反映压电悬臂梁实际输出特性。

为了分析轨道车辆零碳感知用压电俘能结构发电特性，利用无量纲工程模型分别研究了不同无量纲平方压电力压转换因子下，无量纲压电负载与最大归一化输出功率关系；不同机械品质因子下，频率比与最大归一化输出功率关系、最大归一化输出功率随频率比和无量纲压电负载变化关系。

图11 为不同无量纲平方压电力压转换因子下，无量纲压电负载与最大归一化输出功率关系曲线。图11 表明无量纲平方压电力压转换因子的增大对压电梁的最大归一化输出功率产生较大影响，且无量纲平方压电力压转换因子值越大，归一化输出功率也越大。归一化输出功率随着无量纲压电负载的增大至最大值，随后逐步减小，存在最优无量纲压电负载使得轨道车辆零碳感知压电俘能输出功率最大。

图12 为不同机械品质因子下，频率比与最大归一化输出功率关系曲线。从图12 可以看出，机械品质因子值的增加对压电梁的最大归一化输出功率并无影响，而对频率比带宽有明显的影响。机械品质因子值大小代表着压电梁对激励频率选择性的强弱，随着机械品质因子值的增大，频率选择性越强。

图13 为最大归一化输出功率随频率比和无量纲压电负载变化关系曲线。从图13 可以得出，当频率比值固定时，最大归一化输出功率随无量纲压电负载值的增大呈现出先增大后减小的趋势，当达到0.8 附近时，趋近于极限值1，输出功率最大。同样，当无量纲压电负载值固定时，最大归一化输出功率随频率比值的增大呈现出先增大后减小的趋势，当频率比达到1附近时，输出功率趋近于极限值1。因此，当无量纲平方压电力压转换因子与机械品质因子一定的情况下，频率比值为1与无量纲压电负载为0.8 时，轨道车辆零碳感知压电俘能输出性能达到最佳。

3 结论

1) 无量纲平方压电力压转换因子值越大，归一化输出功率也越大。归一化输出功率随着无量纲压电负载的增加呈现先增加后减小的趋势，且存在最优无量纲压电负载使得输出功率最大。

2) 对于双端固支式压电梁结构，增大压电悬臂梁的机械品质因子值，不会影响最大归一化输出功率，但会减小其频率比带宽，即提高压电梁的频率选择能力。

3) 当压电梁的机械品质因子值和无量纲平方压电力压转换因子值固定时，最大归一化输出功率受到频率比值和无量纲压电负载共同作用影响，且在频率比值为1 与无量纲压电负载为0.8 时，压电悬臂梁输出性能达到最佳。

4) 在谐振频率处，理论计算值与仿真值及实测值之间的最大绝对功率偏差分别为0.035 mW 和0.019 mW，对应的相对偏差百分比为2.390%和1.297%；最大绝对峰值电压偏差为0.065 V 和0.035 V，对应的相对偏差百分比为1.201% 和0.647%。基于无量纲模型构建的压电悬臂梁模型不仅在保障模型精度的前提下实现了模型简化，而且更能反映压电悬臂梁实际输出特性。