建筑坍塌事故发生机理的尖点突变模型及应用

2022-10-22李珏韩梅

铁道科学与工程学报 2022年9期

李珏，韩梅

(1. 长沙理工大学交通运输工程学院，湖南长沙 410114；2. 长沙理工大学交通基础设施智慧建造与运维管理湖南省高等学校重点实验室，湖南长沙 410114)

近年来，我国经济发展迅速，建筑业作为我国的经济支柱产业也在快速发展。由于建筑业具有施工人数多、作业强度大、危险系数高等特点，建筑事故发生频率很高，特别是坍塌事故平均死亡率为1.9，远高于所有事故的平均死亡率1.2。坍塌事故一旦发生，极易造成巨大的伤亡情况和严重的财产损失。目前，相关学者对坍塌事故的研究已经取得一定的进展。YANG 等[1]用灰色关联分析法找出坍塌事故的关键因素，从而确定了预防事故的关键措施。崔益源等[2]利用模糊概率量化法对坍塌事故风险因素进行了评价，并通过重要度分析提出了降低坍塌事故发生的措施。郑霞忠等[3]提出将解释结构模型与D-S证据理论相结合的坍塌事故致因诊断方法。通过对坍塌事故的分析可以发现，在事故发生前，施工系统一直保持安全状态，直到突然发生不安全事件，即事故的发生过程是突变的。传统的事故致因模型很难直观地解释事故发生前后系统安全状态突然发生的变化[4]。因此，有学者引入突变理论用于安全工程领域的事故致因分析，来研究事故发生的突变性。在海上交通安全方面，利用尖点突变模型分析海上交通事故的致因机理[5]。在煤矿安全方面，建立瓦斯爆炸事故的尖点突变演化模型，指出事故演化是流变-突变的过程[6]。在铁路安全方面，利用突变理论对铁路事故演化进行量化分析，将系统安全的动态特性和突变特性融入铁路系统风险分析[7]。在建筑安全领域，1995 年，钱新明等[8]将突变理论应用于建筑事故致因分析，建立尖点突变模型分析事故致因过程，提出提高系统安全性的原则。2006 年，YIU 等[9]将突变理论应用于建筑施工过程中产生的冲突行为，定量分析了冲突行为的动态过程。随后突变理论逐步应用于建筑工人不安全行为、挂篮施工安全评价等方面的研究[10-11]。从已有的研究成果来看，大多从静态、实证角度对坍塌事故致因和安全评价进行分析，而对事故形成的机理分析较少。突变理论在建筑安全领域的事故分析中应用较少且多停留在定性分析的层面，特别是在建筑坍塌事故中还没有应用。因此，本文以突变理论为基础，构建坍塌事故的动态尖点突变模型，分析坍塌事故的发生机理，然后从风险源的角度出发，建立风险-事故突变树，利用历史数据进行仿真，研究事故中各风险因素之间的相互作用引起的系统状态变化过程，以期为坍塌事故的预防提供新思路。

1 坍塌事故尖点突变模型构建与机理分析

1.1 模型介绍

突变理论是法国数学家Thom 于20 世纪60 年代中期提出的，它是以奇点理论、稳定性理论为主要基础，研究非连续变化和突变现象拓扑结构的一种理论，利用系统的势函数将系统的临界点分类，研究临界点附近的不连续特征，从而探究自然界和社会系统在连续发展过程中出现的突变现象[12]。根据突变理论可知，系统势函数由控制变量和状态变量来表示，一个系统的状态变量受不小于1 个但不超过5 个控制变量的控制。常用的突变模型通常有5 种，分别是折叠突变(FC)、尖点突变(CC)、燕尾突变(SC)、蝴蝶突变(BC)以及印第安茅舍突变(WC)。一般情况下，突变现象具有以下基本特征：多模态性、突变性、分叉性、不可达性和滞后性[13]。一般认为所研究的问题只要满足2个以上特征，就可以运用突变理论建立模型进行分析。已有研究证明安全事故同时符合突变模型所需特征要求[14]，因此，本文将尖点突变理论应用于坍塌事故分析。

1.2 模型的构建

设任何一个动态系统在任意时刻的状态都可由给定系统的状态变量和控制变量表示，控制变量的值确定状态变量的值。系统的状态可以公式化为一组非线性系统状态方程：

式中：X=(x1，x2，…，xi，…，xn)T是系统的状态变量；F=(f1，f2，…，fi，…，fn)是系统的状态变量对于时间的变化率函数。对系统势函数求1阶导数可得平衡曲面，求2阶导数可得奇点集[15]。

利用泰勒级数展开式将非线性系统转换为突变势函数的形式[16]。进行泰勒展开后，经整理可得尖点突变的标准势函数V(x)、平衡曲面M和奇点集S分别如式(2)～式(4)所示。

通过联立式(3)和式(4)可得尖点突变的分叉集方程B：

式中：x代表系统的状态变量；u和v分别代表系统的控制变量。

由于施工安全系统的特殊性，系统的安全状态、控制变量均存在与实际相对应的临界平衡点。因此，在实际应用中，需对尖点突变模型的一般势函数进行完善。本文根据时间节点对坍塌事故的尖点突变数据进行量化表示，对尖点突变模型完善如下：

其中：ui(t)和vj(t)分别代表t时刻所对应的2 个控制变量；αi和βj为事故原因系数；hi和gj为系统固有特征量，分别代表控制变量对应的临界平衡点。根据上述建模公式可绘制出坍塌事故的尖点突变模型如图1所示。

1.3 突变机理分析

突变理论认为，平衡曲面上控制变量的演化曲线越靠近折叠面，系统越危险，只有演化曲线的投影落在分歧点集中的控制变量才能使得此时的系统处于2 个模态转变的过程[17]。当v的情况不断恶化时，系统所处的状态取决于u的情况。如果u处于良好状态，演化曲线不会经过中叶不可达区域，其投影与分叉集无交点。当u处于较差状态时，会对施工系统安全状态产生不良影响，最终造成严重危害。当u的状态不断恶化时，系统的状态取决于v的情况。如果v状况良好，坍塌事故发生的可能性较小。当v的状态恶劣时，控制变量演化曲线投影落入分歧点集的可能性增加，系统由危险状态突变成事故状态的概率也相应增加。当2个控制变量同时恶化时，事故发生的概率会大幅度增加，并且事故的严重程度取决于控制变量的演化曲线投影与分歧点集相交的长度，相交长度越长说明控制变量的突跳值越大，造成的事故后果越严重，可能会导致较严重的伤亡和财产损失。反之，突跳值越小造成的后果影响一般也较轻，可能导致工人轻微受伤和较小的经济损失。可见，可以通过系统势函数突跳释放的能量大小来判断坍塌事故的严重程度。

2 坍塌系统变量因素的提取和变量的量化

为构建可计算的模型并对模型进行数据拟合及仿真，需要对变量进行量化。从国家住房城乡建设部、安全管理网站、全国各省市相关的行政管理部门网站收集了2013～2019 年的坍塌事故报告246 份，筛选出有详细事故原因的事故报告237份，利用237份事故报告对系统控制变量因素进行提取并对关键指标进行量化。

2.1 变量因素的提取

将人的因素(R)、物的因素(W)、环境因素(H)和管理因素(G)造成的事故原因作为尖点突变模型中的控制变量。通过对237例坍塌事故调查报告的研究分析以及对坍塌事故相关文献的阅读，确定了坍塌事故的事故原因。其中，人的因素包括安全意识淡薄、缺乏安全知识、身体及思想状态不好、违规违章作业、施工单位无资质施工等；物的因素包括机器设备发生故障、使用劣质建筑材料、支护结构强度不同、墙体强度和稳定性不足等；环境因素包括地质条件差、地基失稳、作业环境不良等；管理因素包括教育培训不到位、未进行安全检查、管理人员监管不到位、安全制度不健全等。

2.2 关键参数的量化

为了对模型进行仿真计算，需要对系统的控制变量u和v以及系统固有特征量h和g进行量化，具体公式如下：

式中：n代表死亡人数；p代表重伤人数；l代表轻伤人数；SCA代表事故原因造成的等效死亡人数；PCAi代表事故原因i发生的概率；PCAj代表事故原因j发生的概率；z代表事故原因造成的经济损失当量。

3 参数的确定

3.1 系数的确定

设系统状态变量x在[xmin，xmax]内可以取任意实数，取值越大，表示系统安全状态越好[18]。为了准确描述尖点突变模型，需要确定式(7)中的系数αi和βj。

当系统中的控制变量u和v的状态都处于最佳状态时，系统的安全状态最好，即ui(t)=0，vj(t)=0，此时系统安全状态指标x取最大值xmax，得到图1 中平衡曲面上叶的最高点坐标R(u，v，x)=R(0，0，xmax)。当系统中的控制变量u和v的状态都处于最差状态时，系统的安全状态最差，此时系统安全状态指标x取最小值xmin，得到图1中平衡曲面上叶的最低点坐标T(u，v，x)=T(0，vj，tj，xmin)。在图1中，存在一个平衡曲面上叶与下叶开始分化的点，即为点O，它在控制平面上的投影为O'。根据变化过程m1→n1，m2→O→n2，m3→e3→f3→n3在控制平面上的投影m′1→n′1，m′2→O'→n′2，m′3→f′3→n′3。当ui(t)＞hi，系统不会发生突变；当ui(t)=hi，即将发生突变；当ui(t)＜hi，系统发生突变；当ui(t)=hi，vj(t)=gj，系统的安全状态x取值为0，则发生突变的点为(hi，gj，O)，将R和T的坐标代入式(8)，经计算可得系数ai和bj的表达式：

3.2 突变风险值的确定

为了清晰直观的表达系统的风险变化情况，将风险量化，用ΔVCCij t(x)表示系统的突变风险值，它显示了尖点突变对整个坍塌系统的风险影响，并反映了坍塌事故控制变量的变化趋势[16]。根据式(8)可得x1，x2和x3：

由式(7)，(16)～(19)可得突变前后的风险值：

系统内所有尖点突变的总风险值为：

4 实例分析

4.1 事故案例

以2019 年5 月16 日上海市发生的重大坍塌事故为背景进行案例分析，以呈现该方法的具体计算过程和可视化输出。事故描述具体如下：A公司把厂房整体交B公司管理，但B公司把①幢厂房租赁给C 公司(该公司为事故厂房①幢的二期建设单位)，C 公司的代表人雇佣自然人施工，经过层层转包，2019 年5 月15 日，①幢厂房突然坍塌，造成12 名作业人员死亡，10 名作业人员重伤，2 名管理人员和1名作业人员轻伤，事故造成的直接经济损约为3 430 万元。有关该事故更具体的信息，详见上海政府网站关于长宁区昭化路148号①幢厂房“5.16”坍塌重大事故调查报告。

4.2 案例事故RACT的建立

建筑施工坍塌事故涉及的组织较多，组织间的关系较为复杂，事故的发生是系统中所有风险因素相互作用的结果，普通的线性分析方法不适合用来分析坍塌事故这种复杂的系统。因此，本文使用HUANG 等[16]提出的“风险-事故突变树”(Risk-Accident Catastrophe Tree，RACT)，以阐明风险因素如何导致事故的过程。RACT是通过树状网络结构来展现事故中的风险源(RS)、由风险源造成的事故原因(CA)以及这些事故原因中的突变现象。根据事故报告，该事故的RACT 框架如图2 所示，该图显示了事故的整个过程。

4.3 仿真分析

由于本文主要研究尖点突变模型的事故致因机理，因此仅提供关于尖点突变模型的分析。本案例涉及的尖点突变模型的具体控制变量如表1所示。尖点突变模型的参数值如表2 所示，表2 中的参数值主要是根据公式(11)～(15)计算而来，本文将系统状态变量的最大值设为1，最小值设为-1[16]。尖点突变模型的计算结果如表3 所示。从表2 中的统计数据可以发现，与人相关的风险因素造成的后果最严重，这意味着与人相关的风险因素是尖点突变模型中最重要的控制变量。由表3 可知，风险能量的释放导致系统风险的积累，因此系统尖点突变前后总风险值是不断上升的。

表1 5个尖点突变模型控制变量的详细描述Table 1 A detailed description of the control variables of the five cusp catastrophe models

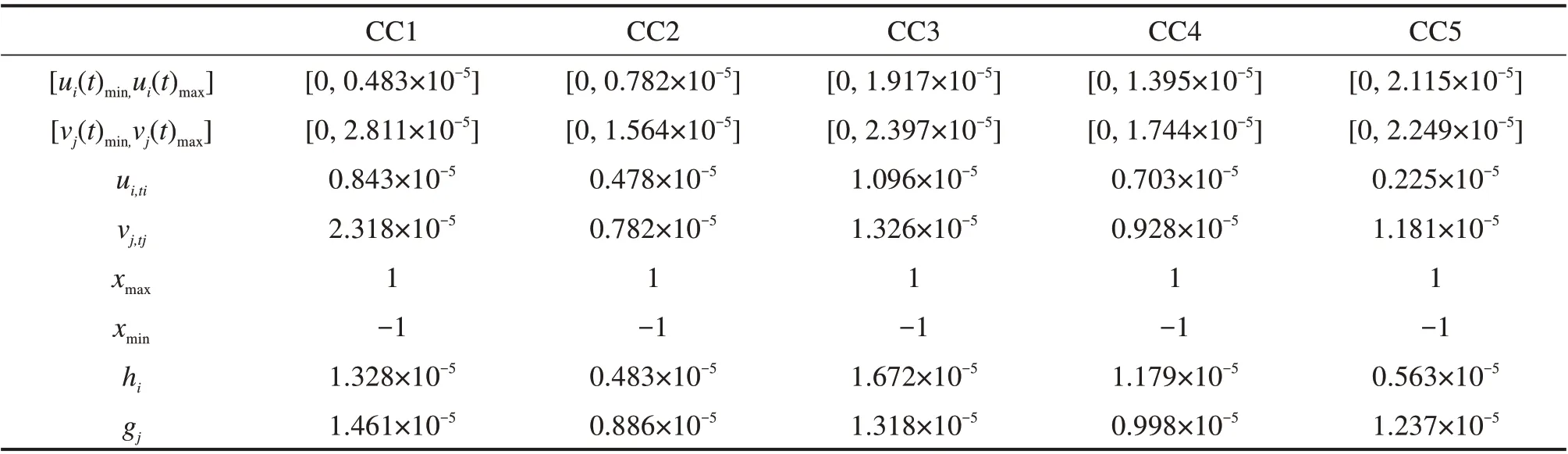
表2 5个尖点突变模型所需要的参数Table 2 Parameter values required for the five cusp catastrophe models

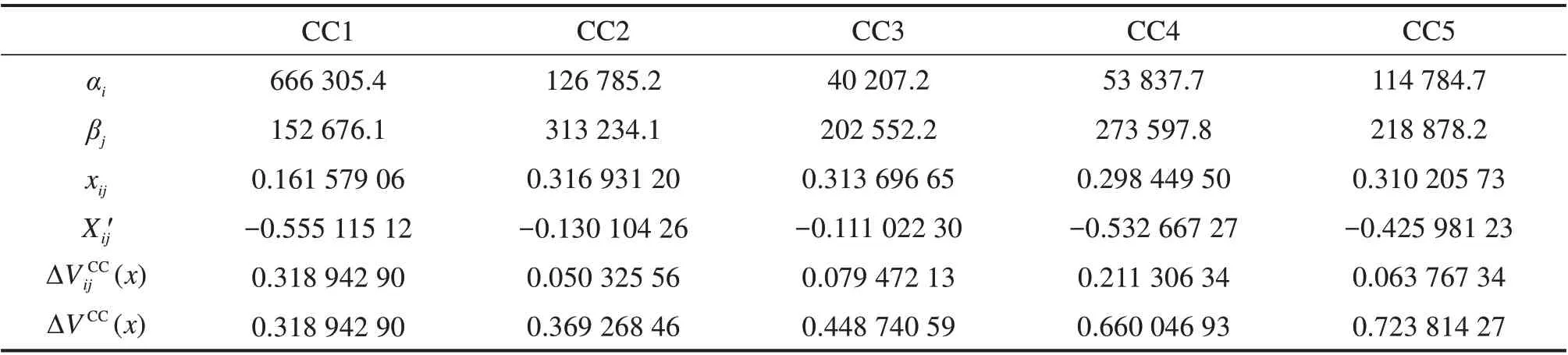
表3 5个尖点突变模型的计算结果Table 3 Calculation results of the five cusp catastrophe models

利用Python 对本案例涉及的尖点突变数据进行仿真，结果如图3 所示。图3 中的5 个尖点突变模型的平衡曲面展现了此次坍塌事故中风险因素的演化路径。平衡曲面由3个部分组成，顶部浅色部分为上叶，代表系统的状态良好；底部深色部分为下叶，代表系统处于极度危险状态或事故状态；中叶为不可达区域，表示作业系统发生突变现象，即从安全状态突变到危险状态。在这个演化过程中，尖点面形状的变化反映的是系统安全性的变化过程，即尖点曲面的折叠程度可以反映系统在当前条件下的整体安全性，尖点面的折叠程度越低，系统越安全，尖端表面的折叠程度越高，系统越危险。分叉集的2条分叉曲线的位置由控制变量v决定，尖点的位置由控制变量u决定。

由图3 可知，图3(a)的折叠程度、演化曲线跨越分叉集的程度最大，且由表3可知CC1的风险突变值为0.318 942 90，是5 个尖点突变模型中的最大值，代表这2个控制变量对该系统的影响是最大的，控制变量为建设单位将项目违规发包给个人和建设项目违规报建。此刻，系统已经处于危险状态，但是由于本次突变处于本案例项目的开端，施工环境较为良好，项目处于可控状态，并未发生事故。随着时间的推移，CC2 的控制变量为施工单位违规允许个人挂靠和施工单位超资质承揽工程，控制量的演化曲线如图3(b)所示，控制变量跨越了分歧点集，但是风险突变值较小，对系统整体影响不大。图3(c)和图3(d) 2 个平衡曲面的演化曲线的投影均与分歧点集相交，因此这2条轨迹呈现突变状态。随着控制变量v的作用程度不断增加，到达分歧点附近时，控制变量u的作用程度开始增加，当控制变量的作用程度越过安全施工的阈值产生突跳时，便极易发生坍塌事故。尽管上文提及的2条曲线的投影与分叉点集有交互，但是2 种曲线与分叉集相交区域的长度是不相同的，由此，可推断出虽然2条轨迹都存在突变，但由于控制变量u和v之间的作用程度不同，其突变强度也存在差异性，因此造成的事故后果也存在较大的差异。由图3 可以看出，CC3 突变强度较小，CC4较大，CC3 对应的突变造成的后果会导致工人受伤和较小的经济损失，而CC4 对应的突变过程会导致人员伤亡和严重的经济损失。CC5 的突变风险值虽然不大，但此时系统累计的突变风险值已经达到了危险状态，系统极不稳定，很容易发生事故。

由系统尖点突变模型可知，当分叉集的有效面积越大，系统控制因素曲线的投影也越容易与分叉集相交，只要系统控制点的轨迹与分叉集相交，则系统中必然存在尖点突变。此时，系统控制点贯穿折叠面，同时伴随着系统风险能量急剧提升，在能量积蓄过程中，系统的信息、结构以及行为都会随时间推移发生改变，甚至破坏。虽然坍塌事故发生与否存在较强的不确定性和突发性，但是可以从预防的角度，对控制变量进行干预，从而达到一定的防控效果。通过所建立的突变模型来分析坍塌事故的致因突变机理，从而为坍塌事故的预控提供一种新的思路。对于可以预判的事故，即2个控制变量都处于可控范围内，通过改变控制变量的状态，从而降低或消除事故发生的可能性，例如提前对施工人员进行安全教育培训、施工前对地基条件进行检测等。对于已经发生的事故，可积极发挥人的主观能动性，在合适的时间进入系统，对控制变量的演化曲线进行有限控制，推迟演化曲线落入分歧点集的时间，迅速采取有效措施及应急预案，减少突跳值，防止事故的恶化与扩大。