地下综合交通枢纽上盖建筑环境振动预测评估<br/>——以北京城市副中心站综合交通枢纽为例

地下综合交通枢纽上盖建筑环境振动预测评估
——以北京城市副中心站综合交通枢纽为例

2022-10-21张登科陈旭超何远鹏

噪声与振动控制 2022年5期

张登科，赵磊，刘文，陈旭超，何远鹏，成功

（1.北京京投交通枢纽投资有限公司，北京 100101；2.北京市市政工程设计研究总院有限公司，北京 100082；3.西南交通大学牵引动力国家重点实验室，成都 610031）

中国地铁建设在进入21世纪以来突飞猛进，运营里程显著增加，但想要大力发展地铁项目，仅靠政府财政往往不能平衡，因此，在如何解决地铁建设资金问题的大背景下，较为成熟的“地铁+上盖物业”，即：以公共交通为导向的城市开发模式（TOD）模式逐渐受到推崇。同时，地下综合交通枢纽在织补城市、创造高品质公共空间、集约用地以及消除铁路分隔等方面有着天然优势[1]。交通枢纽依托轨道交通设置于地下，枢纽上方土地综合开发利用，形成“站城一体”的枢纽开发模式。

然而TOD区域线路交汇越多、上盖建筑形式复杂，往往容易导致振动和噪声更加突出，对地下枢纽的舒适换乘体验、地上高品质业态的开发造成了不利影响。例如地下高铁站靠近城市的功能中心，地上建筑也更为密集且靠近铁路线路，甚至和车站结构共用基础；此外一定数量的列车在车站正线以中低速穿行，轮轨激励振动会直接作用于建筑结构并在其中传播。如果处理不当，未来高强度的铁路运输（城际铁路、地铁）会给该区域带来大量的建筑环境振动和结构噪声问题，影响该区域人民的工作、居住、身体健康及出行体验，因此在工程的设计期便有必要对这类工况开展环境振动及结构噪声的预测评估研究，使得在项目前期将减振降噪措施有针对性地考虑进规划，一方面满足相关规范，另一方面保证建筑的使用品质。

针对地铁引起的车站与上盖建筑的振动与噪声问题，国内外学者从实测分析与数值仿真两个角度展开了研究。雷晓燕等[2]对某一大型综合交通枢纽车站的站房振动进行了实测，分析得到了不同楼层的振动主频。周凌宇等[3]对地铁车站内站厅层的振动与噪声进行了测试，并对振动与噪声超标的房间加装吸声板、吸声棉、与减振垫，测试了其减振降噪效果。谢伟平等[4]通过实测与有限元模拟，计算分析了一栋高11 层的上盖建筑的振动响应，结果表明：上盖建筑的振动成分由列车激励荷载决定，集中在40 Hz 附近；建筑内铅垂向的Z 振级随楼层上升，呈现先降低后增大的趋势。邹超[5]对地铁车辆段附近的多种上盖建筑的振动进行了实测，发现垂向振动在上盖建筑的顶层有放大效应；并研究了隔振沟填充物的优化设计方案，结果表明在建筑物振动的主要频段内，空沟的隔振效果最好。王一干等[6]对车辆段与上盖建筑的振动噪声进行了实测，研究了地铁引起的建筑振动与二次结构噪声，发现两者在频域上具有高度的一致性，验证了根据楼板振动计算房屋二次噪声的经验公式。Guo 等[7]对一座三层地铁停车场的振动进行研究，测量了振动加速度，并进行了数值模拟，提出垂向振动比横向振动显著，是主要的评价指标。Yang等[8]对一大型车站枢纽结构的振动进行了有限元计算，通过预测分析发现对建筑物基础安装钢弹簧浮置板能取得较好的隔振效果。

目前的研究更多集中于轨道交通车站的环境振动或地铁在隧道中下穿通过引起的建筑物振动，对轨道直接落于建筑物楼板的工况研究较少，同时国内存在着几个相关标准对城市区域的环境振动和二次结构噪声进行规范，需要针对这些情况开展预测研究。北京城市副中心站综合交通枢纽位于北京市通州区0101街区，枢纽范围三条国铁线路及三条地铁线路交汇，交通枢纽依托城际铁路设置于地下，枢纽上方采用共构方式建设现代化城市综合体，城市副中心站有创造高品质公共空间开发需求。因此，本文依托北京城市副中心站综合交通枢纽工程，以模型计算的方法为基础，对国内现行的评价标准开展振动及噪声的综合对比，研究枢纽上部建筑的振动特性，计算并比较不同轨道减振措施对环境振动及二次结构噪声的影响，对提升综合交通枢纽开发品质有重要意义。

1 模型预测方法

1.1 车辆模型

采用多刚体半车模型，包含车体、转向架、轮对以及一二系悬挂。列车的振动微分方程为：

式（1）中物理量含义如下：

Mvh——列车质量矩阵；Cvh——列车阻尼矩阵；

Kvh——列车刚度矩阵。

Qvh（t）——列车等效载荷向量；uvh（t）——列车位移向量。

1.2 轨道模型

轨道系统从上至下依次为钢轨，轨道扣件，轨道板，减振垫，底座板。钢轨与轨道板模拟为连续支撑的欧拉梁模型，扣件与减振垫考虑为阻尼弹簧，底座板考虑为刚性。在模型中，单个扣件的节点刚度除以扣件间距，得到每延米的刚度作为计算值。

轨道方程在波数域有如下形式：

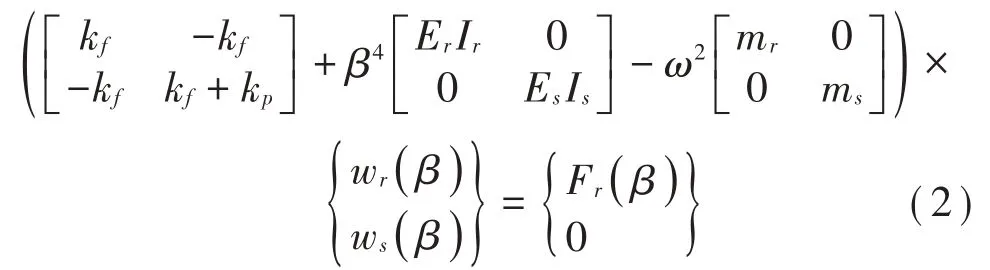
式（2）中：kf为扣件刚度，kp为减振垫刚度，ErIr为钢轨的弯曲刚度，EsIs为轨道板的弯曲刚度，mr为钢轨的质量，ms为轨道板的质量，wr为钢轨的垂向位移，ws为轨道板的垂向位移。

1.3 轮轨相互作用模型

轮轨之间的动态相互作用力是系统的激励源，对于200 Hz以内的轮轨系统的振动，长波不平顺的幅值引起的振动占主导地位。本文采用文献中提出的基于轨道垂向不平顺的垂向激励模型，通过该模型进行计算，得到轮轨系统对应于不同波长的单位粗糙度下的轮轨力响应，再结合轨道不平顺功率谱，即可得到系统的输入激励。

轮轨耦合模型如图1所示。轮对与钢轨之间为赫兹接触，假设轮对与钢轨不发生分离，可得轮轨之间位移匹配方程：

图1 垂向轮轨耦合模型

式中：σrlk表示钢轨上第l和k两个轮轨接触点之间的位移传递函数，可通过对式（2）进行傅里叶逆变换求得。σwlk表示车辆中第l 和k个轮对之间的位移传递函数，可通过列车系统的柔度矩阵进行计算。已知粗糙度幅值，可以计算得到轮轨力幅值

1.4 枢纽-土层有限元模型

由于隧道-大地结构具有长度方向无限长，且横截面大的特性，如果用三维数值模型对其进行计算会消耗大量的算力。然而，列车长度较长，故可将列车与隧道土层的相互作用看作平面应变问题，利用二维有限元模型进行简化计算。有限元模型如图2所示。

图2 枢纽-土层有限元模型

1.5 建筑有限元模型

由于建筑物相对于车站体量较小，因此可以采用子结构的方式进行建模，在计算地表振动时不考虑房屋结构的耦合。以枢纽范围内一栋27 层公寓为例开展室内振动及二次结构噪声规律研究。公寓建筑高度100 m，钢筋混凝土框架剪力墙结构，房屋结构模型如图3 所示。其中，有限元模型主梁和侧梁由BEAM188 单元建立复合梁，楼板和承重墙等由SHELL63 单元建立，混凝土弹性模量为3.6×1010Pa，泊松比为0.2，密度为2 400 kg/m3，损失因子为0.1。钢材弹性模量为2.1×1011Pa，泊松比为0.3，密度为7 800 kg/m3，损失因子为0.01。

图3 建筑三维有限元模型

1.6 模型预测方法验证

为验证计算方法的可靠性和有效性，选取北京地铁15 号线现场测试数据与文中的模型预测方法进行对比。测试断面情况：测试点布设在直线段上如图4至图5所示；60 kg/m钢轨，材质为U71Mn；道床为短枕式整体道床，混凝土强度等级为C35，圆形隧道地段道床断面宽为2 300 mm，道床设两侧水沟，每侧水沟宽为300 mm（圆形隧道及U 形槽地段水沟延至结构边墙）；采用DTⅥ2无挡肩弹性分开式扣件，扣件垂直静刚度为20 kN / mm～40 kN/mm，一组扣件的防爬阻力不小于11.5 kN，轨距调整量为+8 mm、-12 mm，水平调整量一般为30 mm；扣件布置间距均为600 mm，轨面埋深20.6 m；根据实测数据表明，列车运行速度平均值为70.01 km/h。测试内容包括：轮轨垂、横向力；钢轨垂、横向位移和轨枕垂向位移；钢轨、轨枕、道床、隧道壁加速度。

图4 北京地铁15号线测试现场

图5 测试现场传感器布置图

地铁车辆为B型车，车辆6节编组（4M+2T），轴距2.2米，轴重不大于14吨。考虑地铁轨道状态，将测得的短波不平顺和美国6级谱的长波段得到联合粗糙度谱，如图6所示。

图6 联合不平顺功率谱

采用上文方法建立测试断面有限元模型，车辆计算参数如表1 所示，隧道埋深为17.1 m，内径2.7 m，计算参数如表2 所示。读取模型隧道壁1.2 m 位置1/3 倍频程加速度振级，并与测试数据进行对比（测试数据按照测试标准《GBT19846-2005 机械振动列车通过时引起铁路隧道内部振动的测量》测试获得）。选取线路运营高峰时段（上午8 时、中午12时、晚上8时）各10组（共30组）测试数据进行分析。

表1 车辆模型参数

表2 隧道-大地模型参数

考虑车速为70 km/h 计算得到整个模型的振动响应，同时与实测数据进行对比，结果如图7 所示，在8 Hz～80 Hz范围内，隧道壁振动加速度级的模拟值和实测值的绝对误差不超过5 dB。考虑到问题的复杂性，我们认为模型和方法基本能反映实测情况，可用于本项目的研究。

图7 仿真模型对比验证

2 上盖建筑环境振动及结构噪声评价标准横向对比

利用上文模型计算得到枢纽-土层的振动加速度，将其施加在建筑底部，便可计算建筑物的振动及二次结构噪声。

2.1 环境振动评价标准对比

对交通枢纽进行环境振动影响评价，应结合枢纽功能定位、地上建筑业态布局，以及枢纽所在地环境功能区划选择适当的振动评价标准，而目前常用的振动评价标准有GB10070-1988[9]和JGJ/T170-2009[10]。枢纽上盖建筑的功能定位较为丰富（具有商业、公寓和办公等功能），因此将其归类为居住、商业混合区、商业中心区，同时该交通枢纽的上盖建筑和地下车站为一个整体，建筑物室外0.5 m的测点位于车站混凝土板上方，和室内一楼的振动差异较小，本节的评价敏感点都位于室内房屋的中点。

图8 给出了基于两个振动评价标准：GB 10070-1988和JGJ/T170-2009得到的该建筑不同楼层的Z振级。

图8 两个振动评价标准得到的不同楼层Z振级

图中可以看到：

（1）随着楼层的增加，Z振级总体随着楼层的增加而减小，在顶层附近会出现增大的现象，1楼和26楼的三分之一倍频分频振级（未计权）对比如图9所示，可以看到虽然顶楼相比于底层的31.5 Hz以上的高频振动得到了衰减，但顶楼在10 Hz 以下的低频振动却会放大，该频率来自该建筑本身的振动模态；

图9 未记权振动级

（2）两个振动评价标准给出的Z 振级在不同楼层显示出一定的差异性，大小和差异幅值在不同楼层也并不相同。10 层以下的楼层，JGJ/T170-2009得到的Z 振级要高于GB10070-1988 得到的Z 振级，其差异值可以达到1 dB。由于分频计权曲线的不同，两个标准的计权曲线如图8所示，可以看到两个标准的计权曲线在10 Hz 以下差异较小，而在该频率以上，两者的差异可以达到5 dB 以上，即经过GB10070-1988 计权的10 Hz 以上分频振动要远低于JGJ/T170-2009计权得到的分频振动；

（3）在20 层以上更高楼层，GB10070-1988 的振级却要高于JGJ/T170-2009 的振级，这主要来自于评价量的不同，50 Hz以上频带的振动随着频率的增加而快速衰减，而其他频带衰减较小（如图9 所示），使得分频最大的振动（JGJ/T170-2009）在总的等效振动（GB10070-1988）所占比例下降；

（4）对于该高层建筑而言，10 层以下的振动仍是振动最容易超标的楼层，因此，采用JGJ/T170-2009得到的评价量要更为安全，同时由表1和表2可以看到，虽然两个评价标准在工业集中区和交通干线两侧区域的限值相同，但是在居住、商业混合区、商业中心区—本高层建筑适用的区域，JGJ/T170-2009 的限值要低于GB10070-1988 限值5 dB（JGJ/T170-2009 规定限值标准为70 dB、67 dB，GB 10070-1988规定限值标准为75 dB、72 dB），加上因为评价量不同引起的1 dB差异，如果评价结果刚好满足GB10070-1988的限值，但却可能会超过JGJ、T170-2009的限值6 dB。

进一步对比不同楼层相同位置的频谱特性，对1楼及26楼未计权振动级进行对比分析，如图9所示。可以看到：随着楼层增加，对于高频振动（30 Hz 以上），有一定的衰减作用，但是对于低频（30 Hz 以下），由于房屋结构类似于悬臂梁，在端部其低频振动可能会被放大，因此对于高层房屋结构应注意低层不超标但是高层超标的现象。对比两个振动评价标准（GB10070-1988和JGJ/T170-2009）在振动计权上的区别，标准中规定的振动分频计权曲线如图10所示。

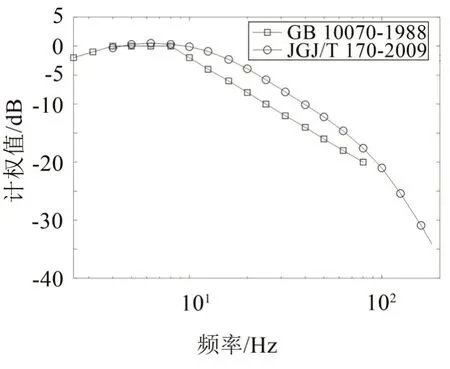
图10 不同标准的振动分频计权曲线

可以看到：GB10070-1988 的计权值要小于JGJ/T170-2009，在相同条件下，JGJ/T170-2009的振动加速度级比GB10070-1988 大，因此根据JGJ/T170-2009计算结果更易超标。

根据VGG-16网络中卷积层的特点,以SeLU作为激活函数的ResNet,神经网络层的解决率和深度值如表1和表2所示。

2.2 结构噪声评价标准对比

由于建筑结构振动基本上均能满足标准要求，因此参考HJ453-2018[11]规定对建筑结构二次结构噪声进行评估。

基于两个结构噪声评价标准（GB/T50355-2018[12]和JGJ/T170-2009）得到的该建筑不同楼层的声压评价值如图11所示，图中虚线代表两个标准的限值，由图9 可知轨道交通引起的该建筑物结构振动能量主要分布在1/1 倍频中的63 Hz 中心频带处，这里只对63 Hz频带进行分析。

图11（a）至图11（b）中对比可知，基于JGJ/T170-2009 进行评价，除1、2 层其他楼层的结构噪声都可以满足限值要求，而基于GB/T 50355-2018进行评价，其63 Hz 倍频程的等效声压级在大部分楼层都有超标的风险，这是因为虽然后者标准的限值比前者高22 dB，但是由于后者标准不对声压进行A计权（对应50 Hz三分之一倍频的记权值为-30 dB），因此63 Hz 频带的结构噪声仍有较大的超标风险。从标准角度，二次结构噪声的超标量大于环境振动。需要注意的是，后者的标准只是针对住宅，在评价商、住两用的公寓时，后者的适用性需要得到进一步的探讨。