含弹性基础压电功能梯度圆柱壳的振动分析

2022-10-21吕志鹏刘文光张宇航

噪声与振动控制 2022年5期

吕志鹏，刘文光，刘超，张宇航

（南昌航空大学航空制造工程学院，南昌 330063）

在航空航天和机械工程领域，振动及振动噪声问题普遍存在[1-3]。这些问题如不加以重视，轻则影响人的健康，重则影响设备的可靠运行。压电智能材料由于其优异的力电转换特性以及对环境具备可感知、可响应和可控制等特点，为结构减振降噪开辟了新途径[4]。结合功能梯度材料（Functionally Graded Materials，简称FGMs）的优越性[5-6]，有研究者将目光集中在两种材料的组合上，以提升压电材料的工程应用价值。

目前，压电功能梯度结构力学问题研究主要分为三大类。第一类主要是利用Maxwell方程或者变分原理直接推导出电学控制方程，对压电功能梯度结构的振动问题开展研究。例如，应用1 阶剪切变形理论并考虑von Kármán 几何非线性，Arefi 等[7]讨论了压电功能梯度圆柱壳的非线性自由振动特性；采用1阶剪切变形理论和微分求积法，段鹏飞[8]探究了热环境下压电功能梯度中厚圆板的自由振动响应；利用等几何分析法，刘涛等[9]研究了不同机械边界条件下压电功能梯度板的自由振动、静态弯曲和变形控制等问题。第二类主要是利用压电材料的逆压电效应，通过对压电层施加电压，探讨结构的静力变形、动力响应和控制问题。例如，应用多尺度法，刘志强[10]系统研究了简谐力和电压激励下压电功能梯度板的非线性动力响应；采用半解析法和考虑几何非线性的Donnell壳理论，Ninh等[11]探究了含弹性基础压电功能梯度碳纳米材料增强圆柱壳在热-力-电荷载作用下的非线性动力响应。第三类主要是利用压电材料的正逆压电效应，令压电材料分别作为压电功能梯度结构的传感层和作动层，开展结构主动控制问题相关研究。例如，基于高阶剪切变形理论和假设模态法，Song 等[12]研究了压电功能梯度碳纳米材料增强板的主动振动控制；应用等几何分析法和Newmark-β积分，刘涛等[13]研究了压电功能梯度层合板的动力学响应与主动控制。利用恒速反馈控制算法和Donnell 壳理论，Dong 等[14]探究了热环境下压电功能梯度石墨烯增强复合圆柱壳的主动控制。

工程实际中，压电结构与其周围弹性介质存在相互作用，陆续有研究者探讨了含弹性基础压电功能梯度结构的振动特性[15-16]。但是鲜有研究讨论多物理场下含弹性基础压电功能梯度圆柱壳的动力学问题，以及压电材料类型对压电功能梯度圆柱壳振动特性的影响。因此，本工作以含双参数弹性基础压电功能梯度圆柱壳为对象，基于一阶剪切变形理论和Hamilton 变分原理，推导多场耦合载荷下压电功能梯度圆柱壳的振动方程，讨论弹性基础、压电材料类型等对模态频率的影响。

1 压电功能梯度圆柱壳模型

如图1所示，Pasternak-Winkler弹性基础压电功能梯度圆柱壳的长度为L，中面半径为R。FGM 层厚度为hf，其表面贴有压电陶瓷，内外压电层厚度分别为hp-I和hp-II。将圆柱壳外层压电陶瓷沿z轴正方向极化，内层压电陶瓷沿z轴负方向极化。在压电功能梯度圆柱壳的中面建立圆柱坐标系（x，θ，z），其中，u0、v0和w0分别表示圆柱壳在轴向、环向及径向的中面位移。考虑压电功能梯度圆柱壳在轴向和径向分别受均匀分布的静态荷载Ax和P的作用。外表面分布Pasternak-Winkler 型弹性基础，其中，Kp为Pasternak 型弹性基础模量，K w为Winkler 型弹性基础模量。

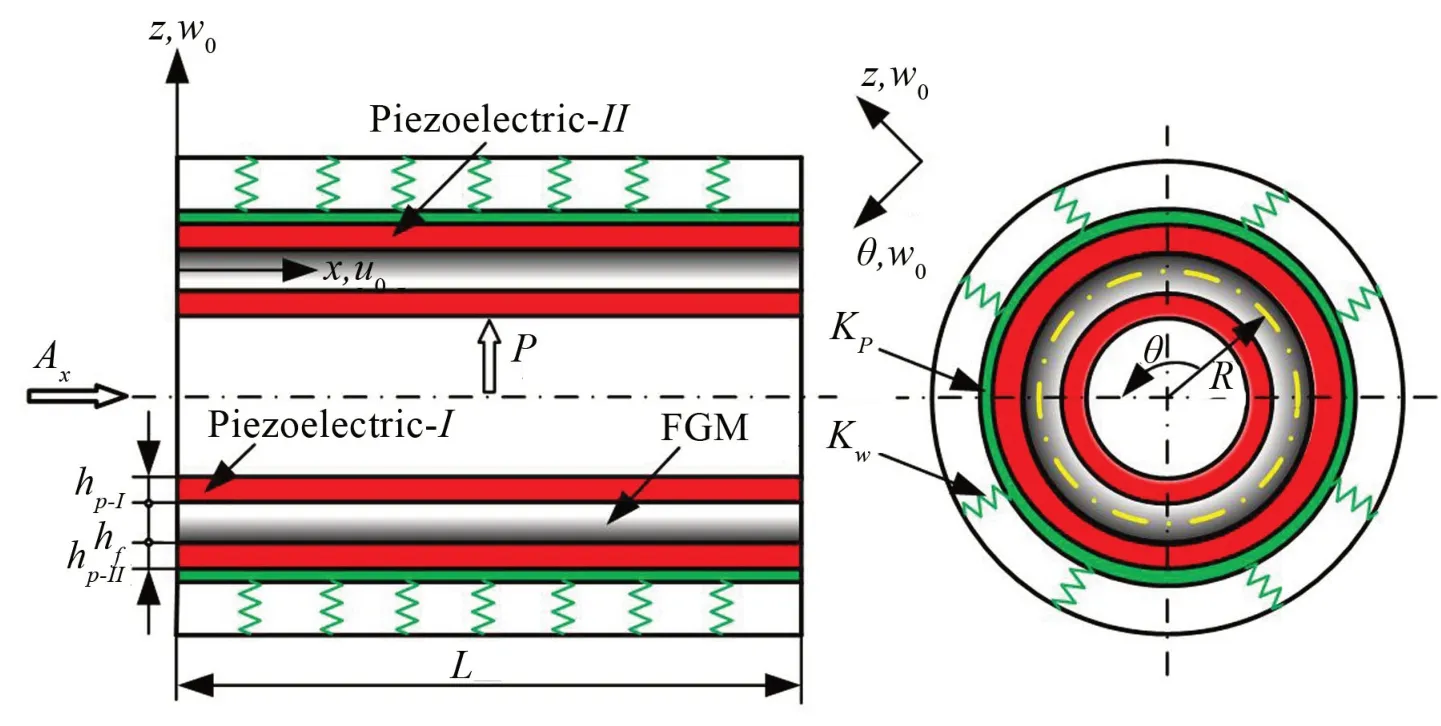
图1 含弹性基础压电功能梯度圆柱壳模型

假设FGM 层的材料组分由内表面陶瓷ZrO2逐渐向外表面金属Ti-6Al-4V 连续梯度变化，FGM 层的有效材料参数可表示为：

式中：Γc和Γm分别表示内外表面的材料参数；N为FGM层的陶瓷体积分数指数。

考虑温度场沿壳体厚度方向呈线性分布，温度场T（z）的表达式为：

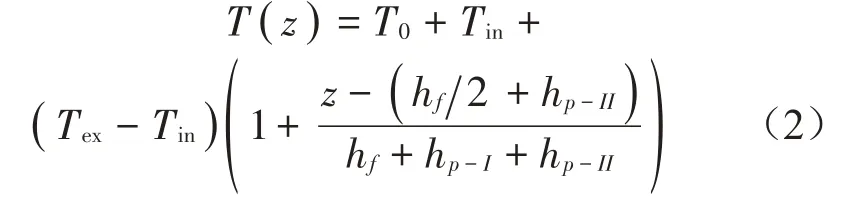
式中：环境温度T0=300 K；Tin和Tex分别为圆柱壳内外表面的温度。

2 压电功能梯度圆柱壳运动方程

根据一阶剪切变形理论，圆柱壳的位移分量为：

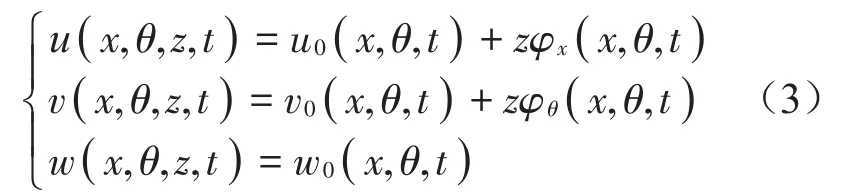
式中：u、v和w分别表示圆柱壳内任意一点的位移分量；φx和φθ为中面法线分别绕x轴和θ轴的转角。

FGM层的应力-应变关系为：

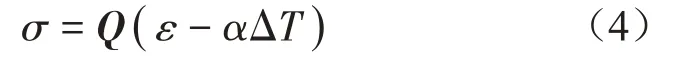
式中：ΔT=T（z）-T0；Q为缩减刚度矩阵；σ、ε和α分别为FGM层的应力、应变和热膨胀常数向量。各矩阵和向量的表达式为：

式中：缩减刚度元素Qijf（i，j=1，2，4，5，6）的表达式为：

式中：Eeff和veff分别为FGM 层的有效弹性模量和泊松比。

热、力、电耦合情形下压电层的本构关系为：

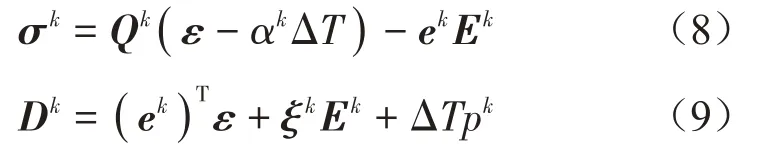
式中：上角标k=I、II分别表示内外压电层；σk、αk、Ek、Dk和pk分别为压电层的应力、等效热膨胀常数、电场、电位移和等效热释电常数向量；Qk、ek、ξk分别为等效弹性常数、等效压电常数和等效介电常数矩阵。这些等效常数可根据平面应力假设得出，具体表达式为：

电场强度与电势之间的关系为：

式中：Θk为在外加控制电势V（t）作用下压电层内的电势分布函数，定义为：

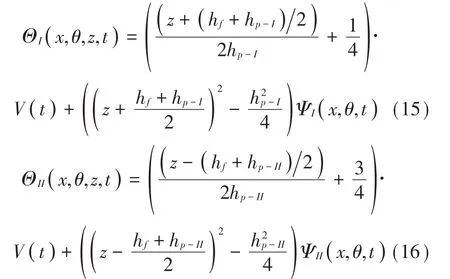
式中：Ψk（x，θ，t）是压电陶瓷因正压电效应产生的诱导电势在面内的分布函数。

压电功能梯度圆柱壳的动能K为：

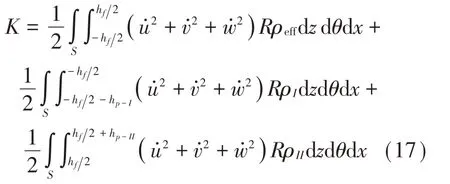
式中：ρeff和ρk分别为FGM层和压电层的材料密度。

压电功能梯度圆柱壳的应变能U为：

式中：

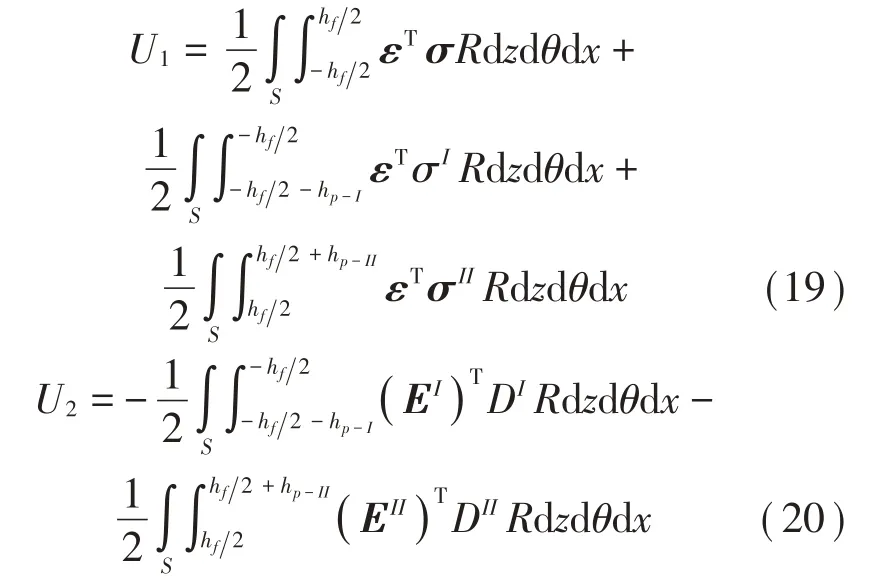
热、力、电荷载所做总功包括[17-18]：

式中：

式中：NTx和NITx分别为温度在FGM 层和压电层的x方向引起的热载荷；Nkex为电压在压电层的x方向引起的电载荷。

根据Hamilton变分原理：

可得压电功能梯度圆柱壳的运动方程：

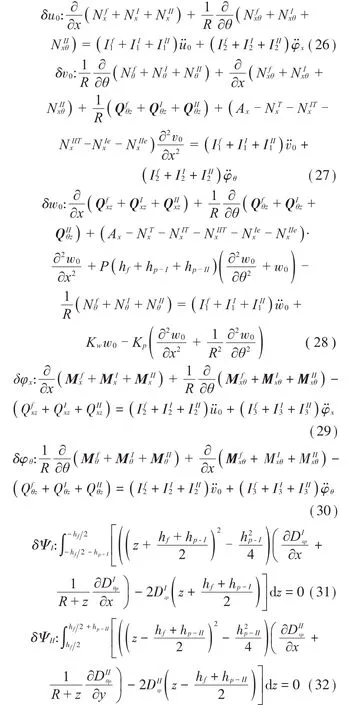
式中：Nfij和Nkij（i，j=x，θ，z）分别为FGM 层和压电层的中面内力；Mfij和Mkij为相应各向力矩；Qfij和Qkij分别为FGM 层和压电层在z方向的剪力；If1、If2和If3为FGM层的广义惯性常数，Ik1、Ik2和Ik3为压电层的广义惯性常数。

3 模态频率方程求解

假设压电功能梯度圆柱壳两端简支，壳的中面位移和电势函数可表示为：

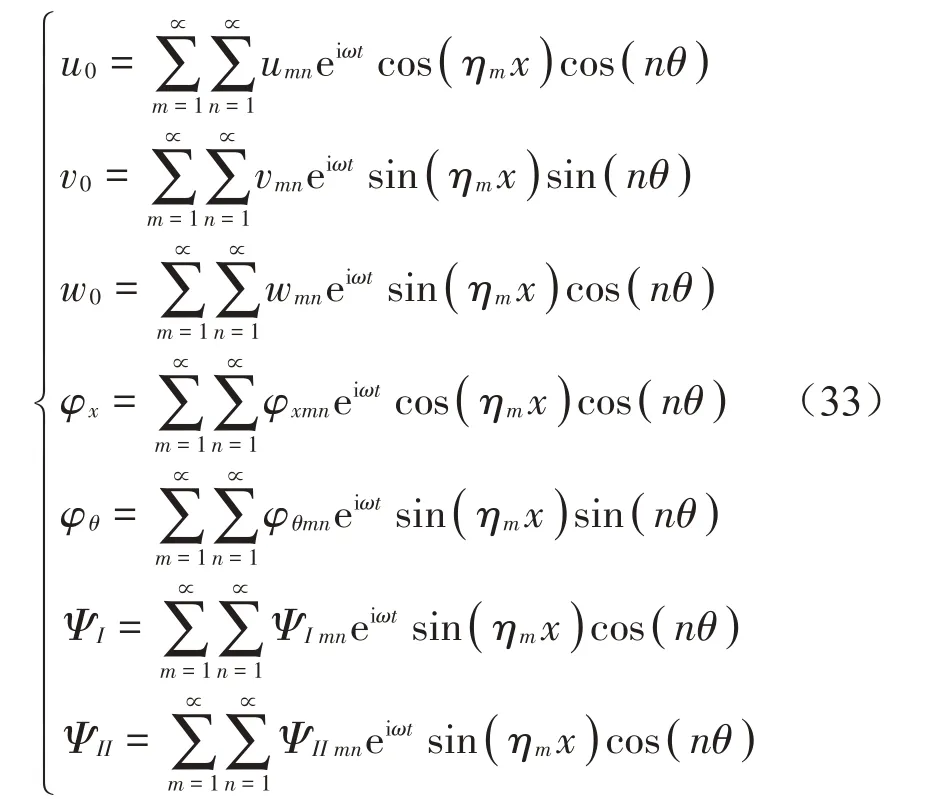
式中：ηm=mπ/L；m和n分别为轴向和环向波数；ω为压电功能梯度圆柱壳的角频率。

综合上述公式得到压电功能梯度圆柱壳在多场作用下的模态频率方程：

式中：M、K分别为广义质量和广义刚度，a为振型系数向量。求解模态方程式（34），可得压电功能梯度圆柱壳的模态频率。

为便于分析，定义以下无量纲参数：

数值计算时，材料参数分别取E=70 GPa，v=0.3，ρ1=2 707 kg/m3，ρ2=30 00 kg/m3，h=0.01 m。为了验证理论推导的合理性，将模型简化为与文献[19]一致的具有单层压电层的压电功能梯度圆柱壳。图2为压电功能梯度圆柱壳模态频率随环向波数的变化趋势。

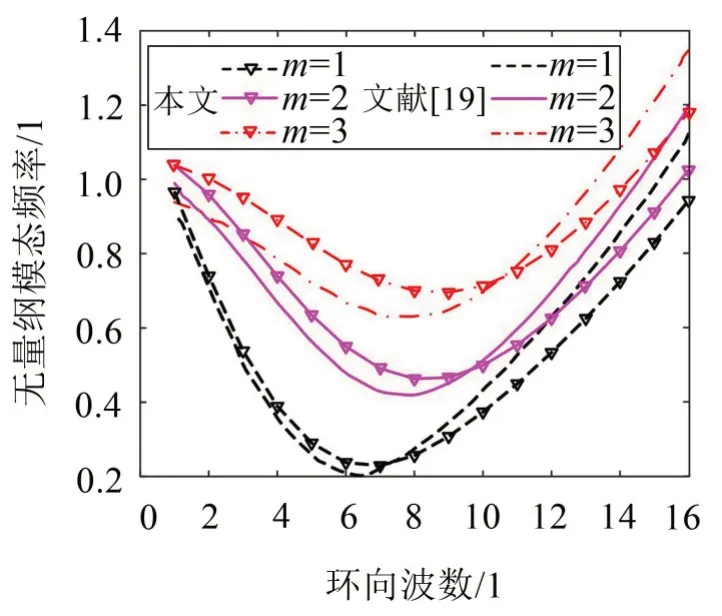
图2 压电功能梯度圆柱壳模态频率随波数的变化

表1为压电功能梯度圆柱壳模态频率与轴向载荷的关系。结果表明，本文模型计算的模态频率与文献[19]结果比较吻合。

表1 压电功能梯度圆柱壳模态频率与轴向载荷的关系

4 分析与讨论

如无特殊说明，压电层选用PZT-4。表2为各种压电陶瓷材料参数。功能梯度材料参数分别取：Ec=168 GPa、Em=105.7 GPa、ρc=3 000 kg/m3、ρm=4 429 kg/m3和υc=υm=0.298；圆柱壳的几何尺寸取：L=10 m、R=1 m 和hp-I=hp-II=hf=0.001 m；轴向和环向波数取：m=3 和n=3；其他参数取：N=1，P1=100，Kw1=Kp1=0.000 1，V=100 V，Ax1=-0.5，Tin=300 K。

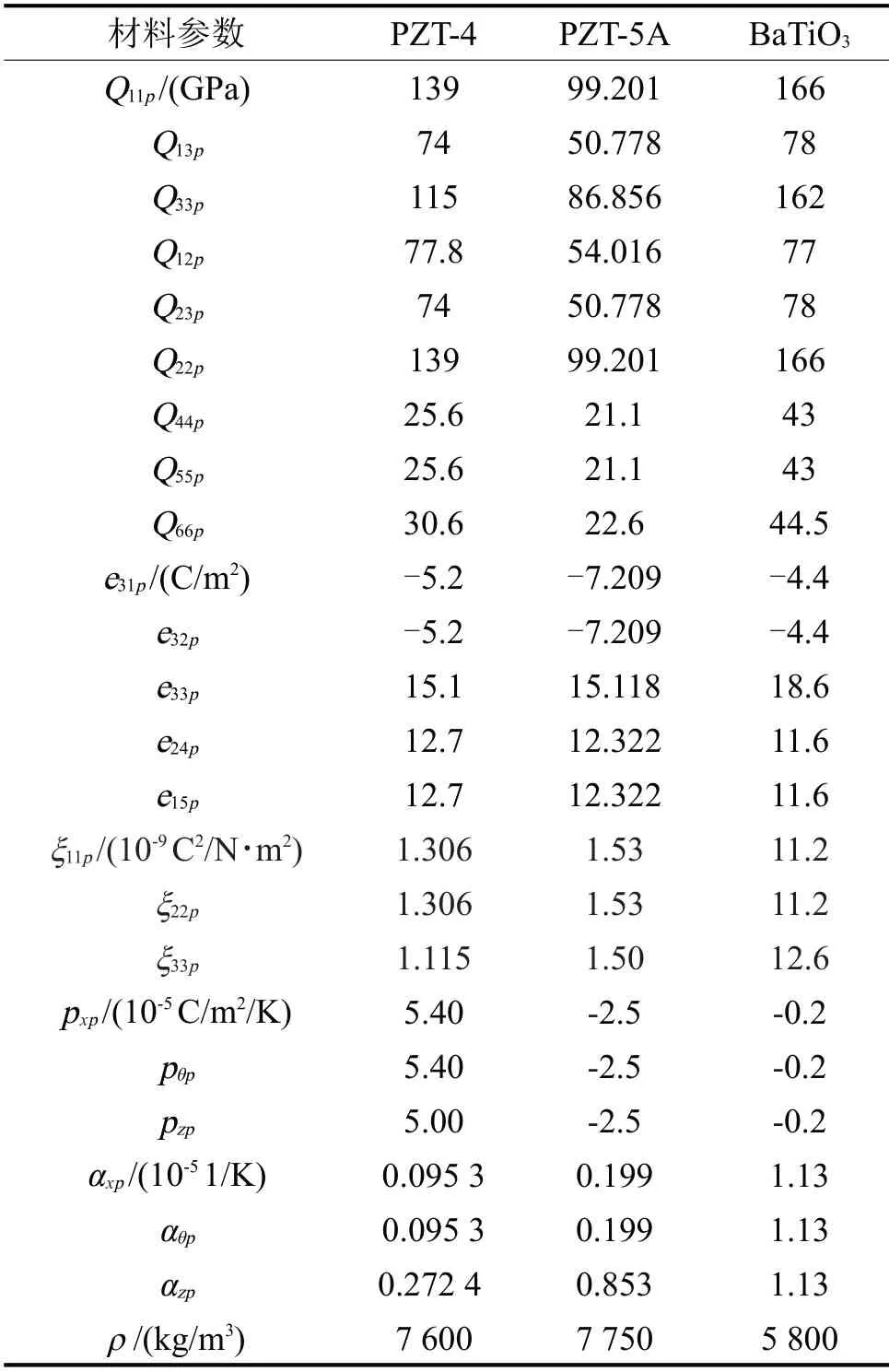
表2 各类压电陶瓷的材料参数[20-22]

如图3所示，研究了不同温度梯度下，无量纲模态频率随弹性基础参数的变化。结果表明：当参数Kw1或Kp1一定，增大Tin会减小圆柱壳的模态频率。这是因为温度降低了圆柱壳的刚度。当Tin一定时，模态频率随着弹性基础参数Kw1的增大基本呈线性递增趋势，随着Kp1的增大呈近似二次函数的形式，而且增长率逐渐减小。说明弹性基础会提高圆柱壳的刚度。对比图3（a）和图3（b），可知弹性基础参数Kp1比Kw1提高模态频率显著。

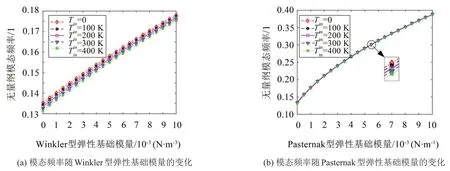
图3 不同温度梯度下模态频率随弹性参数的变化

如图4 所示，研究了不同压电材料时模态频率随弹性参数的变化。结果表明：选用不同材料时，模态频率随弹性参数Kw1或Kp1的变化趋势基本相似。选用PZT-4 和PZT-5A 时模态频率相差不大，选用BaTiO3较其他两种材料较大程度提高模态频率。

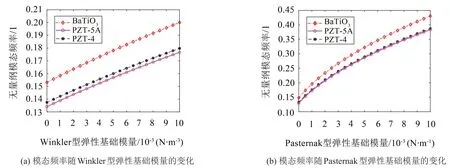
图4 不同压电材料下模态频率随弹性参数的变化

如图5 所示，研究了不同陶瓷体积分数指数N下温度梯度对模态频率的影响。分析表明：Tin一定时，增大FGM 层的陶瓷体积分数指数，结构刚度因陶瓷含量增多而逐渐增大，导致模态频率越来越大。当N增大至5 到10 时，由于材料组分逐渐趋于纯陶瓷，导致模态频率增长率逐渐减小。进一步发现，模态频率下降率随N的增大而逐渐增大。原因在于未考虑FGM 层的材料参数与温度之间的依赖性。否则由于N越大，内部陶瓷含量越多，耐热性越强，结构刚度受Tin的影响也越小。结论表明，当压电功能梯度圆柱壳在较低温度且忽略温度对材料特性的影响时，选用较大的N有利于提高结构刚度，但模态频率下降率却越来越大；结构在较高温度下，不能忽略温度梯度对FGM层的材料特性影响，否则会产生较大误差。

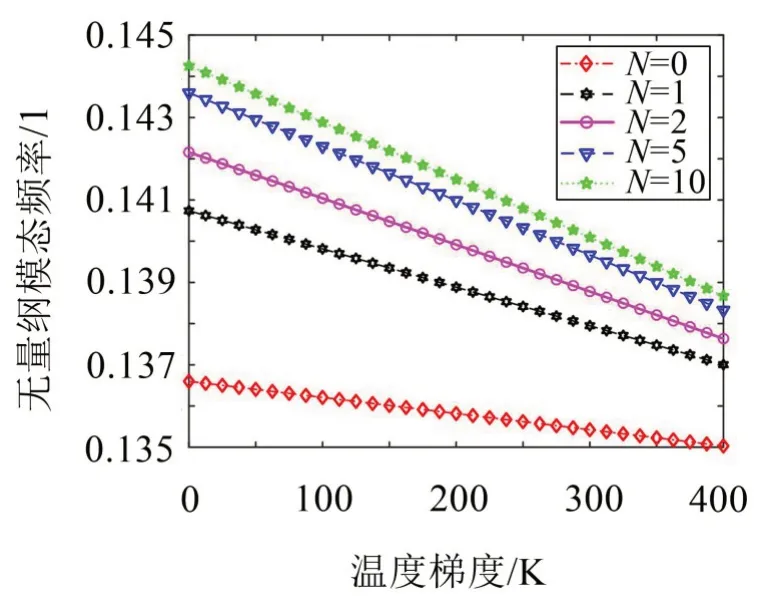
图5 不同陶瓷体积分数下模态频率随温度梯度的变化

如图6所示，研究了不同压电材料下，温度梯度和陶瓷体积分数指数对模态频率的影响。从图6（a）可以得到，Tin一定时，尽管BaTiO3的模态频率最大，但是其刚度受Tin的影响却最大，而PZT-4和PZT-5A对Tin的敏感性基本一致。压电材料对Tin的敏感性由强到弱的顺序依次是BaTiO3＞PZT-4=PZT-5A。从图6（b）可以得到，不同压电材料下，改变FGM 层的N，结构模态频率变化趋势基本一致。且均在N≤2时，模态频率随着N的增大先快速增大，然后逐渐趋于平稳。结论表明，压电材料的种类不影响模态频率随N的变化趋势；为使FGM层含有一定的刚度和强度，N控制在2左右较好。

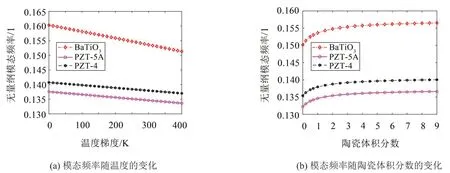
图6 不同材料下模态频率随温度和陶瓷体积分数的变化

如图7 所示，研究了不同温度梯度和压电材料下模态频率随激励电压V的变化。结果显示，不同Tin下，激励电压对模态频率的影响趋势基本一致，且随着激励电压的增大，模态频率出现微小降幅。进一步分析得到，温度梯度相对外激励电压对结构刚度的影响更为显著。图7（b）中Ω/ΩV=0表示结构模态频率与激励电压V=0 时模态频率的比值。可以看到，激励电压对选用PZT-5A 时模态频率的影响最大，而选用BaTiO3时的影响最小。