无叶片风力机捕能柱涡激摆动气动噪声分析
2022-10-21龚曙光谢桂兰卢海山
龚曙光,李 志,谢桂兰,卢海山
(湘潭大学机械工程学院,湖南湘潭 411105)
基于涡激振动的无叶片风力机主要由捕能系统、发电机和连接其两部分的传动装置组成,其中捕能系统由捕能柱和磁性回复装置组成,如图1所示。当风作用在捕能柱上时,会使捕能柱产生风致横向摆动,从而带动发电装置发电[1-2],特别是当涡激脱落频率接近捕能系统的固有频率时,会使捕能柱产生共振,即产生“锁频”,从而使风力机的发电量达到最大。由于无叶片风力机对风能捕捉十分敏感且能迅速进入工作状态,可大幅度提高风能的利用率[3]。它可应用于野外通信机站、小型建筑物、独户的居民住宅等,为实现分布式风能发电提供了可能,因此对无叶片风力机捕能柱的振动噪声开展研究具有非常重要的现实意义。
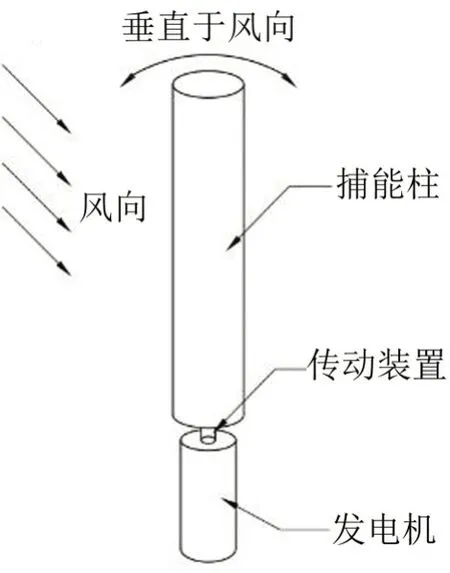
图1 无叶片风力机示意图
针对圆柱体的风致振动噪声,国内外学者已开展了相关的研究,如Cheong 等[4]采用混合数值方法对低马赫数下的圆柱绕流噪声进行了分析。郑朝荣等[5]采用雷诺平均法和宽频带噪声源模型混合方法,对具有不同截面形状和尺寸的柱体在不同来流风速下的气动噪声源特性进行了研究。马瑞贤等[6]通过求解声学线性欧拉方程,模拟分析了圆柱绕流气动噪声的辐射特性。邵卫东等[7]将雷诺平均法和声类比法相结合,研究了圆柱绕流的气动噪声,分析了不同来流速度对远场噪声辐射的影响。蔡建程等[8]通过与实验结果对比,研究了偶极子和四极子源模型在三维圆柱绕流气动噪声预测的准确性。王芳等[9]推导了基于可渗透边界的气动噪声计算模型并对层流圆柱和湍流圆柱进行了气动噪声计算,有效降低了其计算的复杂度。Ⅰglesias等[10]通过实验研究了雷诺数、偏角、攻角、柱体截面形式等对柱体气动噪声的影响。Ma 等[11]采用混合数值方法对二维圆柱体在低雷诺数下的横向受迫振动进行了声学分析,研究了不同频率比(圆柱体振动频率与漩涡脱落频率之比)对噪声辐射的影响。
然而上述文献主要针对静止柱体绕流产生的噪声进行研究,而对柱体的涡激横向摆动,特别是当柱体处于锁频时所产生噪声的机理还有待于进一步的探索。文中采用k-ωSST 湍流模型和声类比法相结合,在模型验证的基础上,对无叶片风力机捕能柱涡激横向摆动噪声进行分析,探讨来流风速对捕能柱涡激振动噪声及远场气动噪声辐射的影响,所得结果将为无叶片风力机的研发提供指导。
1 数值计算理论模型
1.1 固有频率的计算
针对无叶片风力机的结构特点及工作状态,可将其简化为图2 所示的弹簧-质量-阻尼摆动系统振动模型。当捕能柱受到风力作用时,捕能柱在来流向仅产生倾斜(也称平动),在横向将产生绕x轴方向的摆动(捕能柱底部中心为偏转中心),若不考虑捕能柱本身的变形,则其刚性动力学控制方程为:
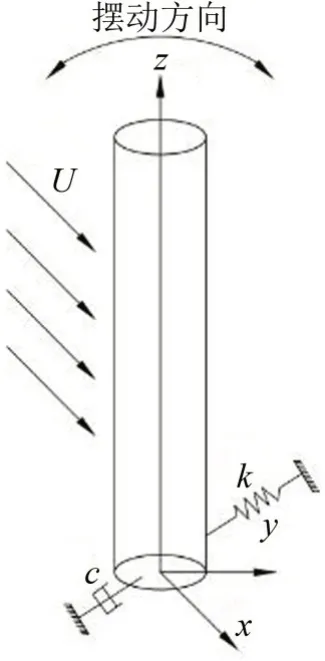
图2 捕能柱摆动模型
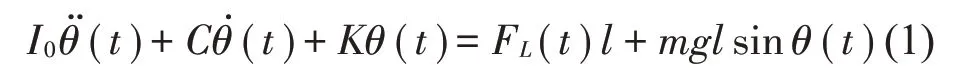
式中:I0为转动惯量;θ为偏转角度;C为阻尼系数;K为磁性回复力矩系数;FL为升力;m为质量;l为捕能柱质心到偏转中心的距离。
因捕能柱的摆动偏转角度不宜过大,因此可认为sinθ≈θ,同时当外力为零时,式(1)简化为:

从式(2)可得到捕能柱的固有频率为:
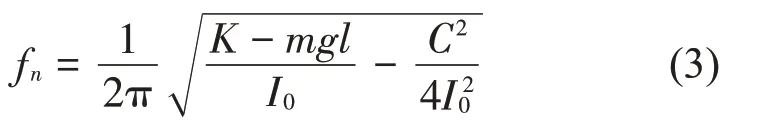
文中,选取捕能柱直径D=0.12 m、长度H为10D、壁厚为0.001 m,其材料为ABS 塑料薄壳(密度为1 020 kg/m3),参考文献[12]取系统阻尼比ζ=0.015,质量阻尼比m×ζ=0.43,其中m*=m/mf,(mf为捕能柱排开流体的质量)。由于系统阻尼比ζ=,可得阻尼系数C=0.636 5 N·m·s/rad(磁性回复力矩系数K取938)。将以上参数代入公式(3)可得捕能柱系统的固有频率为fn=10 Hz。
1.2 流体控制方程
文中通过非定常不可压缩雷诺平均方程求解流体控制方程:

式中:ui为流体速度张量;表示i方向流体的平均速度;ρ为流体密度;p为瞬时压力;v为黏度表示雷诺应力张量。
为保证流场计算的精度及效率,文中在计算过程中首先采用SⅠMPLEC算法对流场进行稳态计算,然后再采用PⅠSO算法进行瞬态计算,所采用的离散格式均为2阶迎风格式。
1.3 声场控制方程
FW-H(Ffowcs Williams-Hawkings)方程是一个不均匀的波动方程,由连续性方程和N-S方程推出,即有:

式中:a0为远场声速;p′为远场声压,p′=p-p0,(p0为声压的参考值);Tij为Lighthill 应力张量;H(f)为Heaviside函数;Pij为应力张量;nj为控制面上单位外法向矢量;ρ为流体密度;ui为流体速度张量;un、vn分别为f=0面上的法向速度和流向速度分量;δ(f)是δ函数。
当流速为低亚音速流动且源表面包围源区域时,式(5)的积分若忽略体积积分,即可得到FW-H方程积分解的形式如下所示。

其中:

式中:r为声源到接收点的距离;t为传播时间;Mi是马赫数向量。
因此通过对结构流场进行分析,将所得到的受力特性以及固体边界运动代入式(7),即可得到相应的载荷噪声。
2 仿真模型及验证
根据图2 的简化模型,本文在仿真分析时选取计算域为35D×20D×10D,如图3 所示,且两侧边界与捕能柱的距离均为10D,出口边界与捕能柱距离为25D。
将流域划分为9个区域,其中捕能柱周围4D范围内采用O型网格,其他区域采用结构网格,网格尺寸逐步递增,其增长率为1.08。同时设置第一层近壁面网格质心到壁面的无量纲距离y+<1,其增长率为1.05;柱体展向网格高度取为0.06D,即为7.2×10-3m,得到的网格模型如图4所示。

图4 网格模型
边界条件设置:左侧设定为速度入口,且为均匀速度;右侧为压力出口;其余边界为对称边界,如图3所示。
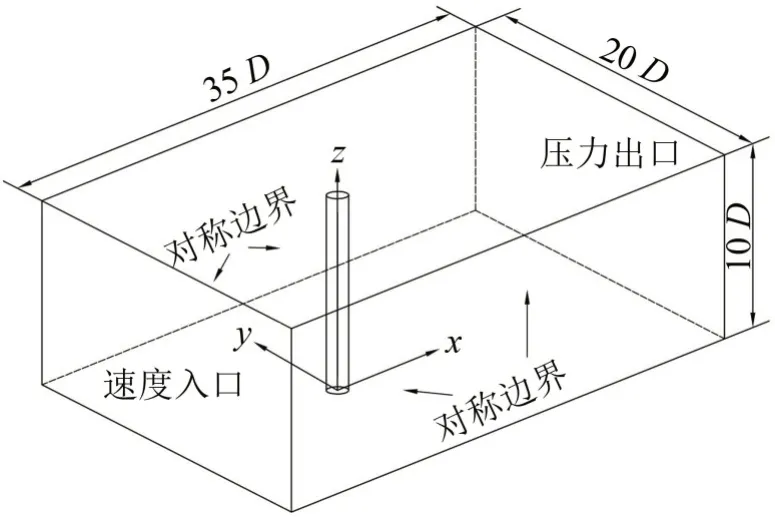
图3 流域及边界条件
采用k-ωSST湍流模型,取雷诺数Re=40 000,不同周向网格数Nc下的涡激振动计算结果如表1所示。

表1 气动力参数比较
对表1 中的结果进行对比,采用Nc=160 的网格并计算了亚临界雷诺数区间内的气动力参数,所得结果与文献[13]的风致振动实验结果进行了对比,两者符合较好,这说明本文所建模型是可行的。
3 仿真结果及讨论
3.1 捕能柱的非定常流场分析
因捕能柱在摆动过程中要受到风压作用以及磁性回复力矩、阻尼力矩和重力力矩的作用,在分析中则需要利用Fluent软件的用户自定义函数来计算捕能柱所承受的作用力,其计算式为风压与重力对柱体产生的力矩矢量和减去该时刻柱体受到的磁性回复力矩和阻尼力矩。
同时结合k-ωSST 湍流模型和6 自由度动网格法,对捕能柱的涡激摆动进行了非定常流场分析。
通过仿真计算,得到了捕能柱横向摆动角度随风速的变化规律如图5所示,图6所示为捕能柱横向摆动频率及漩涡脱落频率随风速的变化规律。
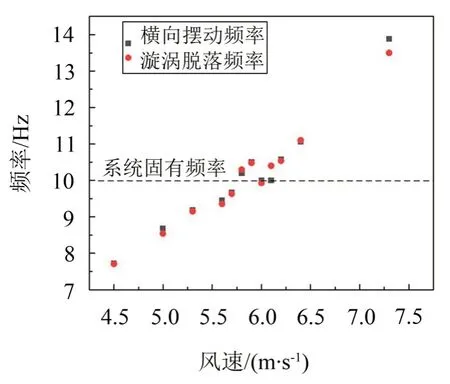
图6 横向摆动频率与漩涡脱落频率随风速的变化
图5显示了捕能柱横向摆动角度随风速的增大出现先增大后减小的趋势,当风速为6.0 m/s 时,其摆动角度达到最大值2.3°,这说明其横向摆动频率接近捕能柱的固有频率(10 Hz),即达到了“锁频”状态。
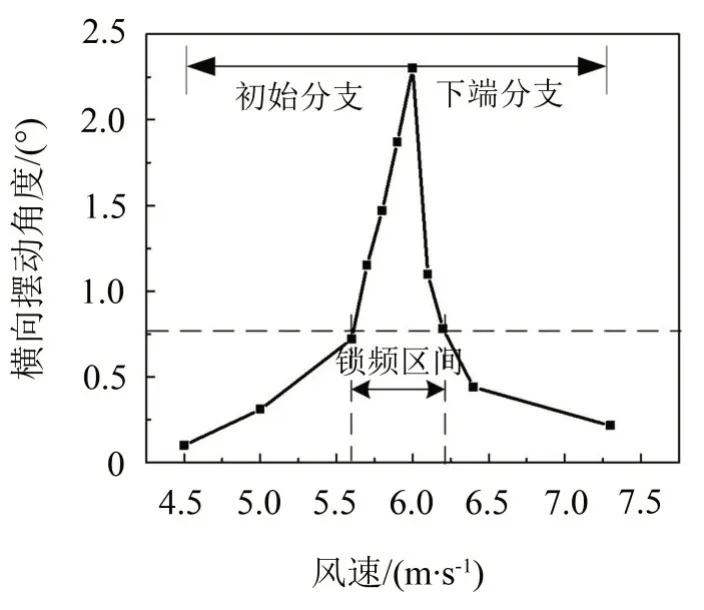
图5 横向摆动角度随风速的变化
同时从图6 可知,捕能柱横向摆动频率和漩涡脱落频率随风速增大而增大,当风速为6.0 m/s 时,漩涡脱落频率和横向摆动频率分别为9.9 Hz和9.82 Hz,均接近且小于系统的固有频率。但从图6 也可看到,其锁频区间较窄,这主要是由于捕能柱的质量比过大所引起。
捕能柱在风速为6.0 m/s 时的响应时程曲线如图7 所示,捕能柱横向摆动在6 s 后趋于稳定,且来流向的倾斜角度在0.2°左右变化,仅为横向摆动角度的8.5%,说明捕能柱两侧形成的漩涡脱落对其横向摆动的影响远远大于来流向摆动。
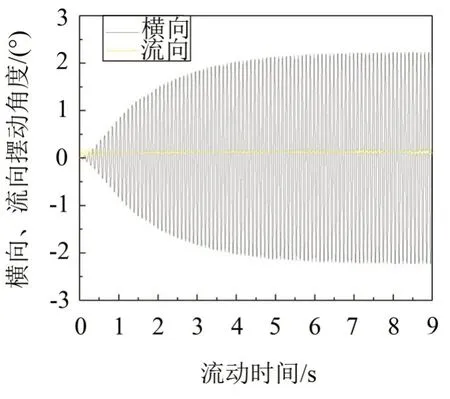
图7 捕能柱摆动角度时程曲线图(6.0 m/s)
3.2 捕能柱的远场噪声分析
将非定常流场分析得到的捕能柱周围声源强度大小以及分布规律,利用波动方程控制与声场有关的量传至远场,最后使用FW-H 方程的积分外推法即可计算捕能柱的远场噪声,其中将忽略流动对声波的影响。
声压级SPL和总声压级OASPL定义为:

式中:p0为声压的参考值(取2×10-5Pa)。
噪声分析时取监测点坐标分别为A(0,10D,-D),B(0,10D,5D),C(0,10D,11D)。通过仿真计算,得到各监测点总声压级随风速的变化规律如图8所示。
由图8 可知,各监测点的总声压级均随风速的增大呈现先增大后下降再提升的趋势,且均在锁频风速时达到最大,其中监测点B 的总声压级为最大即98.6 dB,其次为A 点、C 点,即捕能柱中段的噪声最大,其底部噪声略大于顶部噪声,这说明捕能柱涡激摆动所产生的噪声大小不仅与摆动频率有关,也与摆动角度有关,且捕能柱周期性尾涡脱落所造成附近流场压力的变化也会影响到其声场的变化。同时当捕能柱进入下端分支时由于横向摆动角度减小,使得其噪声总声压级出现了突降现象。
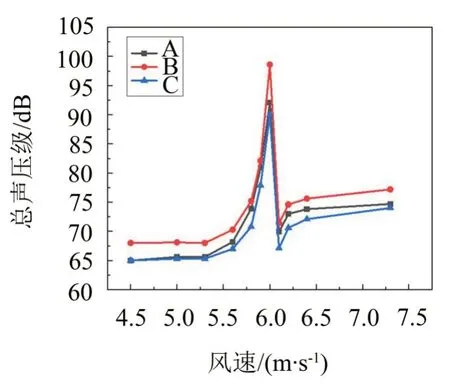
图8 不同监测点总声压级随风速的变化
监测点B、B1(0,20D,5D)、B2(0,30D,5D)和B3(0,-10D,5D)处的声压时程曲线如图9所示。
由图9 可看到,监测点B 与监测点B3之间的声压有Δt=7.06×10-3s的时间滞后,即传播20D的距离,其声速为339.94 m/s。监测点B 和B3的声压脉动幅值相等,但存在180°的相位差;位于捕能柱同侧的监测点B、B1、B2的声压相位相同,但监测点B 的声压幅值明显大于B1和B2,且B至B1的声压衰减要大于B1至B2。同时随着风速的增大其声压也增大。
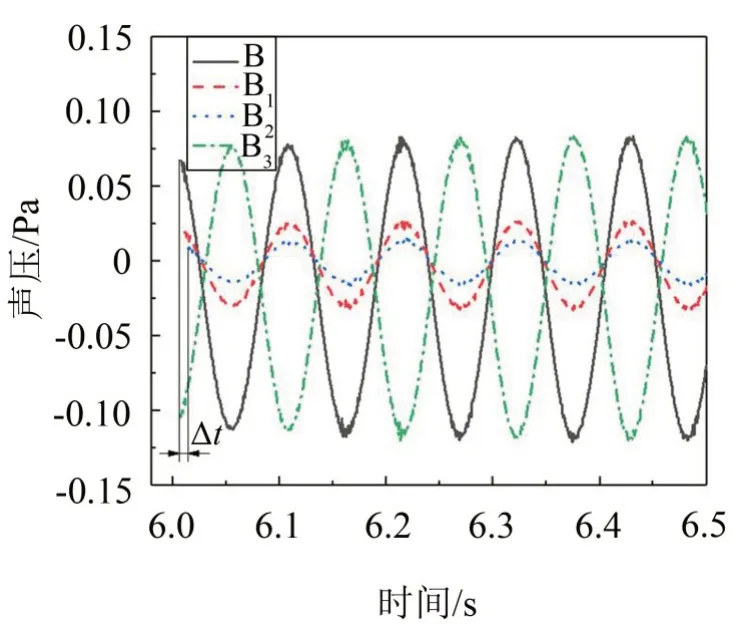
图9 监测点的声压时程曲线(风速为5.6 m/s)
以捕能柱处于平衡状态下的质心为圆心,10D、20D、30D为半径的圆上每隔5°取一个监测点,通过计算得到每个监测点上的总声压级,并绘制成远场噪声声学指向性图如图10所示。
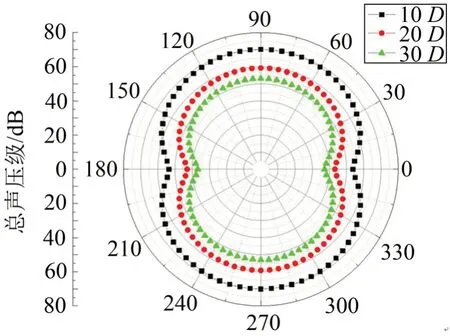
图10 捕能柱远场噪声声学指向性图(风速为5.6 m/s)
由图10可知,捕能柱涡激摆动声场的分布呈现出两侧大、中间小的8字形,与偶极子声源的辐射指向性最为接近,且总声压级最大值出现在横向,即捕能柱的横向摆动方向,而其最小值出现在来流方向。这说明捕能柱在涡激摆动过程中,其两侧周期性漩涡脱落所产生的正负压力脉动,使捕能柱壁面产生了对周围媒介剧烈变化的非定常力,这也是其为偶极子声源的根本原因。
不同风速下捕能柱远场噪声的衰减如图11 所示,图12显示了捕能柱在监测点B的倍频程声压级频谱对比图。
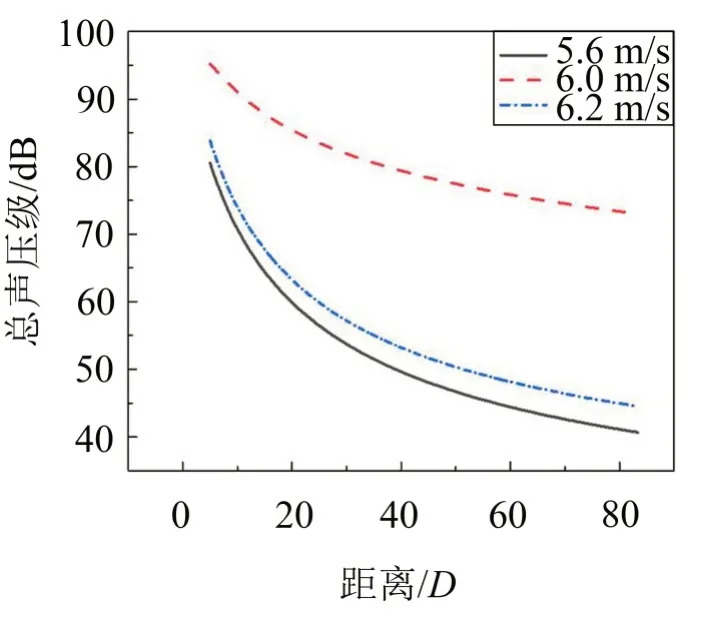
图11 不同风速下捕能柱远场噪声衰减图
由图11可知,捕能柱远场噪声在相同间距内的噪声衰减量并不相同,如当风速为5.6 m/s 时,当距离捕能柱20D范围内时,其衰减量为10.8 dB,而在20D~30D时,其衰减量为6.2 dB,这说明距离捕能柱越近其衰减量越大;同时当位于锁频状态时,其总声压级要明显大于其他风速,且其噪声的衰减率与其他风速相比要小,这说明捕能柱在锁频状态所产生的噪声是主要的控制因素。
从图12可知,当捕能柱处于初始分支阶段风速时,其倍频程声压级峰值所对应的中心频率为8 Hz;当处于下端分支阶段风速时,其频率由8 Hz变为16 Hz;而处于锁频状态即风速为6 m/s时,倍频程声压级峰值所对应的中心频率主要集中在125 Hz~500 Hz,明显大于非锁频风速区间,这表明捕能柱涡激摆动所产生的噪声处于低频范围内即为低频噪声。
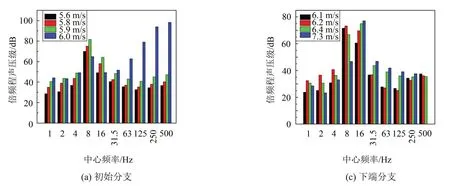
图12 不同风速下捕能柱倍频程噪声频谱
4 结语
(1)捕能柱涡激摆动所产生的噪声在比较宽的频域范围内存在,且所产生的噪声为低频噪声,噪声大小与摆动角度和摆动频率有关。
(2)沿捕能柱高度方向,其中段的噪声最大,且底部的噪声要大于顶端。
(3)距离捕能柱越近噪声衰减量越大,当处于锁频状态时,噪声达到最大,且衰减量要小,这说明锁频状态所产生噪声是主要控制因素。
总之捕能柱远场噪声主要受到横向摆动频率和摆动角度等因素的影响,具体来说主要受到简化模型系统的质量、刚度、阻尼等的影响,这些影响因素将是本文后续研究所要解决的问题。
