雨刮反转过程摩擦特性分析

杨 雪，王岩松，郭 辉，郑立辉，袁 涛，孙 裴

（上海工程技术大学机械与汽车工程学院，上海 201620）

汽车雨刮-风窗系统的减振降噪，能有效改善汽车的NVH（Noise Vibration Harshness）性能，提高乘员舒适性。而减少雨刮-风窗系统的振动噪声，需要对雨刮片的摩擦特性理论进行研究。近十几年来，众多学者从理论建模及实验等角度开展研究，取得了一系列研究成果。

Koenen 等[1]通过实验分析雨刮片运动，并求出了各种条件下的动摩擦系数，得出摩擦系数的值随速度的增加而减小的结论。Deleau 等[2]用不同的弹性体试样对摩擦和擦拭性能之间的关系进行了实验研究，结果表明，在潮湿条件下，定义三种不同速度状态下摩擦系数的变化机制：低速摩擦系数最高，但比干燥条件下要低；中速状态下随着速度的增加而减小；高速状态下摩擦最小。Rouzic等[3]利用单自由度数学模型模拟雨刮器滑动摩擦现象，通过引入Stribeck摩擦定律，预测了雨刮器失稳现象的出现和演变过程。但该模型仅考虑湿润状态，并未考虑其他工况。Lancioni等[4-5]通过对雨刮器非光滑动力学系统的计算，研究了雨刮器运动过程中出现的三类基本振动现象，即高频尖叫、反转振动和低频颤振，建立了雨刮-风窗系统的2 自由度连杆模型，并证明雨刮片在接近反转时法向力大幅增加。陈清爽等[6]对前雨刮器进行了振动噪声实验研究，得到改变刮片结构及增加阻尼材料可以降低摩擦振动的结论。张立军等[7-9]通过实验及理论的角度对雨刮片进行了研究，分析了雨刮-风窗之间摩擦振动和噪声现象及非线性粘滑对平面刮刷的影响，但缺乏不同湿状态下系统反转过程中摩擦振动的理论分析。

上述文献研究了雨刮-风窗系统中雨刮单向刮刷的情况，为了贴合实际情况并详细分析噪声产生的机理，还需要分析雨刮片的反转行为。Goto 等[10]通过实验证明在反转前后都会产生尖叫噪声，并利用有限元法模拟了叶片的振动。Okura 等[11]根据雨刮系统的有限元模型建立了物理模型，模拟了系统在换向过程中的动态特性。基于库仑摩擦假设，Sugita 等[12]建立了以雨刮片转角为变量的单自由度动力学方程，分析了雨刮片反转过程中的正压力变化规律以及随转角变化产生的“分岔”和“混沌”现象。但文献[10]至文献[12]未考虑雨刮实际运行工况中干湿条件需要用不同的摩擦理论模型分析。Unno等[13]的2自由度模型，考虑了动静摩擦的影响，基于松弛变量法，求出了准确过渡时间，并通过仿真和实验，分析了雨刮片在半干燥半湿润状态下的黏着-滑动行为，亦未考虑干湿状况下的摩擦特性。雨刮-风窗系统摩擦副在运行中，干燥和湿润是常见且易产生噪声的工况，因此建立不同干湿工况下雨刮反转过程中的摩擦理论模型，进而研究摩擦特性，对分析摩擦振动噪声的机理十分必要。

1 雨刮反转理论模型

在反转过程中，雨刮片尖部处于静止状态，但在反转前后刮片产生剧烈振动，产生令人不适的噪声[6,10,13]。本文通过物理模型[13]，理论研究上述现象并分析摩擦振动产生的机理，建立系统控制方程并进行无量纲处理，便于摩擦模型的导入。

1.1 雨刮-风窗系统物理模型

雨刮片由头部、窄颈部和位于雨刮片下部的尖部组成，如图1所示并建立单自由度物理分析模型，如图2所示，在模型中，连杆对应刮片中的颈部和尖部；雨刮片头部随雨刮臂在水平方向做往复运动。M表示模型头部的质量，m表示颈部和尖部组成的连杆质量；l表示连杆的长度，l1和l2分别表示连杆重心到颈部支点和刮片尖部的距离；k1和k2分别表示头部与连杆的刚度；lG是弹簧k1的等效自然长度；用I表示连杆在重心处的惯性矩。为使模型更接近实际运行状态，引入两个不同的阻尼系数c1和c2，分别表征当雨刮片肩部不与头部接触时及接触时所产生的阻尼如图2（a）所示。此外，N和F分别是从扫掠表面作用到刚性杆的法向力和摩擦力。

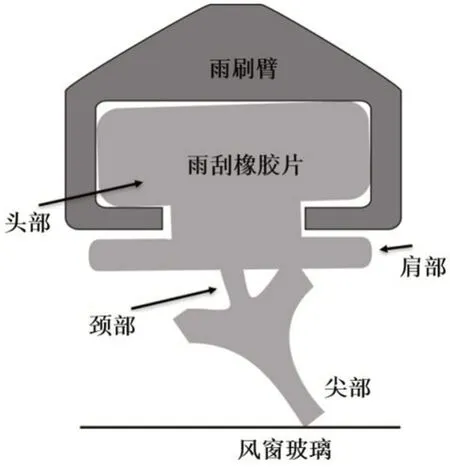
图1 雨刮结构刨面图

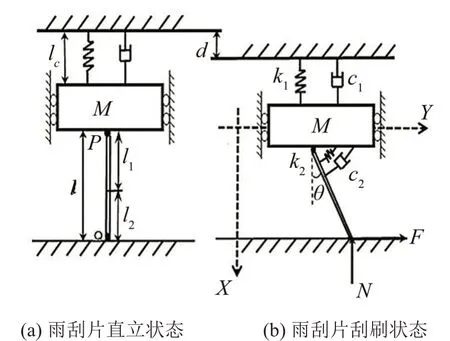
图2 雨刮片物理模型

雨刮-风窗系统的物理模型及动力学模型包含非线性项，推导和求解过程复杂。相对于文献[13]中的2 自由度模型的复杂计算，本文所引用的单自由度模型推导和求解简洁，能较好描述雨刮片反转过程的动态特性，并利于后续的摩擦模型加入；与文献[10]及文献[11]中的三维有限元分析相比，该模型无需考虑复杂的前处理（接触对设置，网格划分等）以及非线性收敛问题，便于求解和分析。

1.2 摩擦系统动力学模型

笛卡尔坐标下的X-Y轴原点设在雨刮片头部水平位置处。刮片静止时系统各部分状态如图2（a）所示，运动时系统各部分的位移如图2（b）所示。其中，角度θ表示叶片与法向轴的夹角；当雨刮橡胶片竖立在玻璃板上时，θ等于零。固定侧在X轴上的位移为d，其中头部的位移为x。此外，施加在雨刮片上的初始压力通过上端的雨刮臂产生；雨刮橡胶片头部与连杆间的连接点记为P，雨刮片尖部顶端上方0.5毫米的点记为Q。

根据达朗贝尔原理[14]，有：

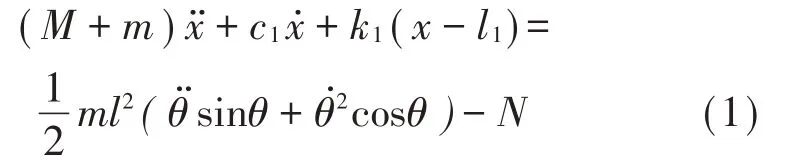
由∑MC=0，P为支撑点：

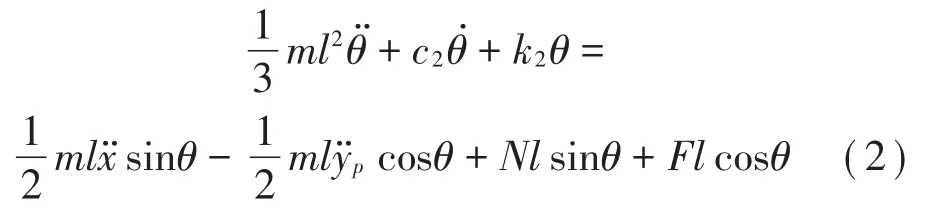
橡胶片整体的约束条件可表示如下：

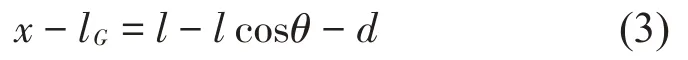
设定固定侧在Y轴方向的往复运动为角频率ω和振幅A的余弦波，P、Q两点的位移条件如下：

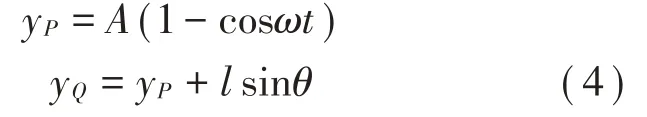
由上述公式可以得到：

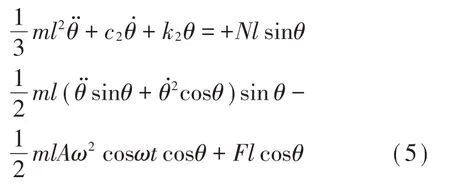
方程无量纲化处理，可减少独立参数的个数，便于后期推导及求解。

x、t、N、F的无量纲变量，即x*、t*、η和χ，定义如下：

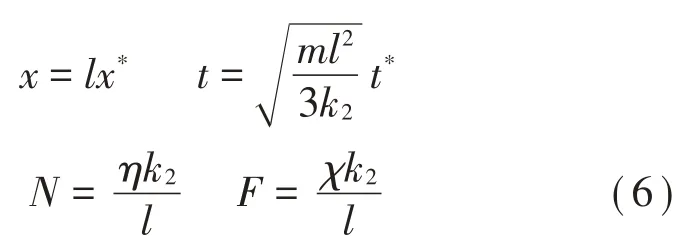
此外，对雨刮片的往复运动yP和雨刮橡胶片尖部水平位移yQ无量纲化：

于是，公式（4）可以用上述定义的无量纲变量表示为：

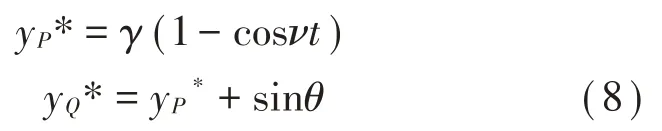
由位移条件进行1 阶导可以得到速度条件如下：

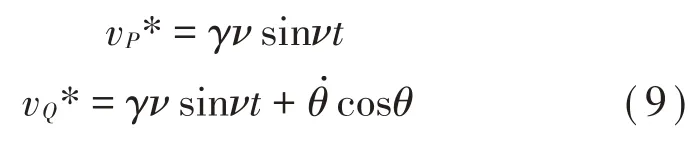
由对公式（1）进行无量纲处理可以得到：

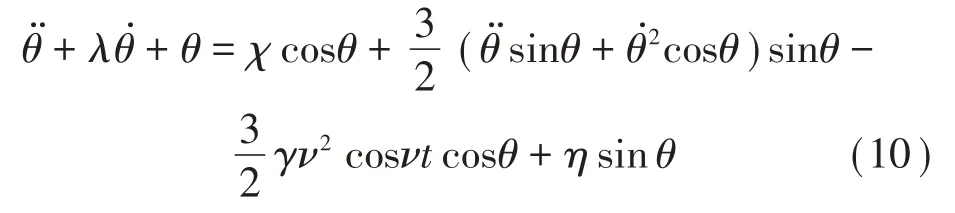
对公式（2）进行无量纲处理可以得到：

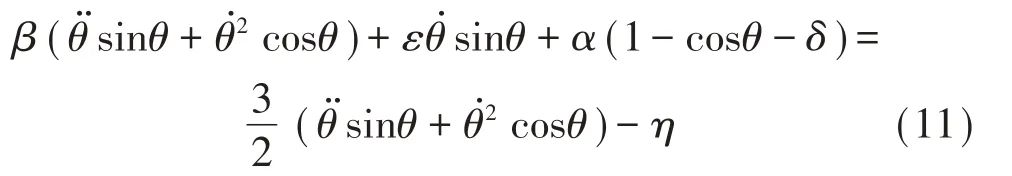
由此可以得到法向力无量纲表达式：

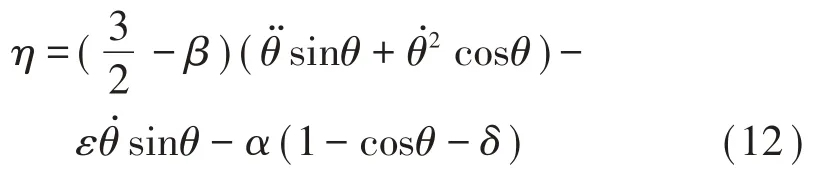
同理，由公式（3）可得：

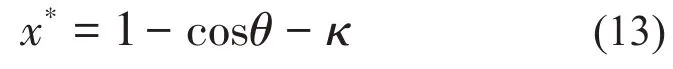
其中：α、β、γ、δ、ε、κ、λ、ν是无量纲参数。部分动力学无量纲参数如表1所示：

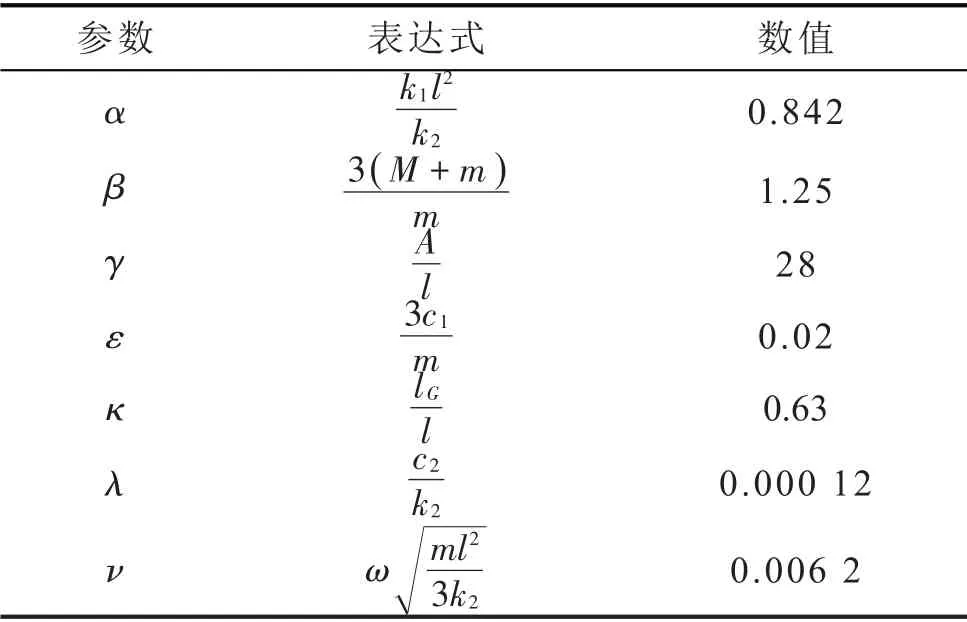
表1 无量纲参数表

2 摩擦模型

针对雨刮片在不同工况下的摩擦力变化及振动情况，本节建立摩擦系数拟合公式；依据库伦（Coulomb）摩擦定律和流体润滑中的库埃特流（Couette flow）特性，分别研究干燥和湿润状态下的摩擦力；为数值求解及振动分析奠定基础。

2.1 摩擦系数模型

系统的摩擦系数在不同工况中有所不同[1]，摩擦系数-相对速度负斜率定律[2,13]表明动摩擦系数受到滑移速度变化影响。本文建立了摩擦系数拟合公式：

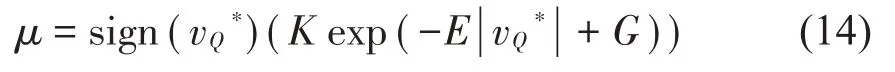
其中刚柔两接触面之间的摩擦系数定为μ，公式可表述为μ=fsign（vQ*）。E、K由运行工况决定，G为常数；sign（vQ*）符号为符号函数，表示形式为：

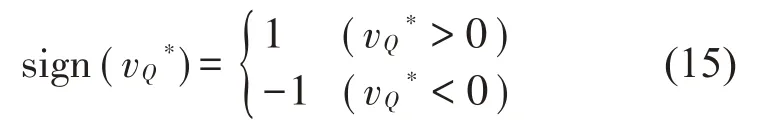
从公式（14）中可知速度vQ*为时域函数，因此，建立摩擦系数随雨刮片周期运动的时域函数：

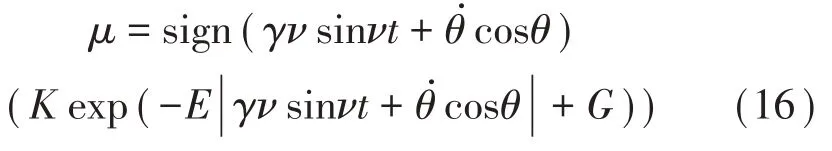
分别定义干燥、湿润状态下的摩擦系数μd、μm的时域公式如下：

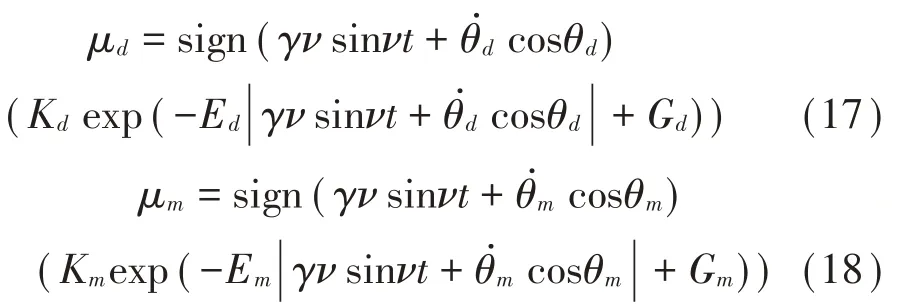
2.2 摩擦力模型

利用摩擦系数的时域变化模型，并结合库伦摩擦定律和流体力，分别分析雨刮片在干、湿状态下的振动及摩擦力。

干燥工况下，摩擦力与法向力成正比关系，其比例系数为摩擦系数，该式可以表示为：

由库伦摩擦定律可知[15-16]，干摩擦中摩擦系数与接触面积、速度以及接触时间无关，但在本文中，需要考虑速度对摩擦系数及摩擦力的影响。

干燥状态下摩擦力的无量纲表达式为：

由公式（10）、式（12）、式（20）可以得到：

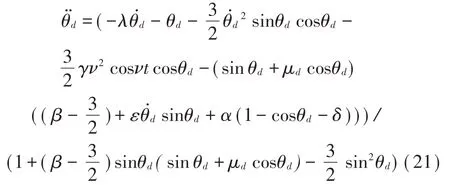
其中：χd、μd、θd分别表示干燥工况的摩擦力、摩擦系数及湿润状态下的角度。

干燥状态摩擦力的时域无量纲表达形式：

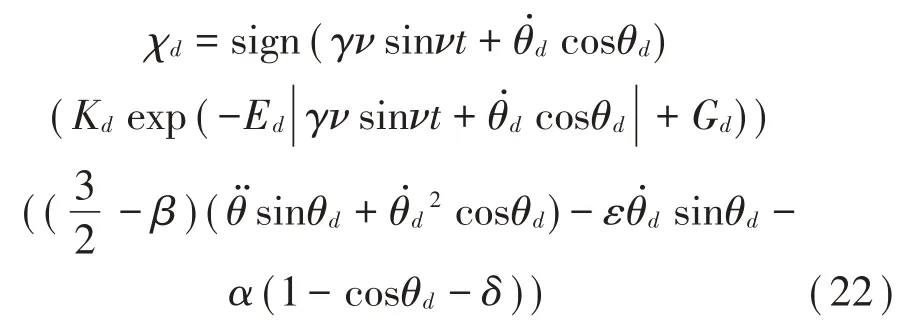
雨刮在湿润状态下运行时，雨刮-风窗接触面形成相对均匀的水膜，其中刮片的厚度约为10 微米（b=10×10-6m），水膜的平均厚度约为10 纳米（=10×10-9m），如图3所示。

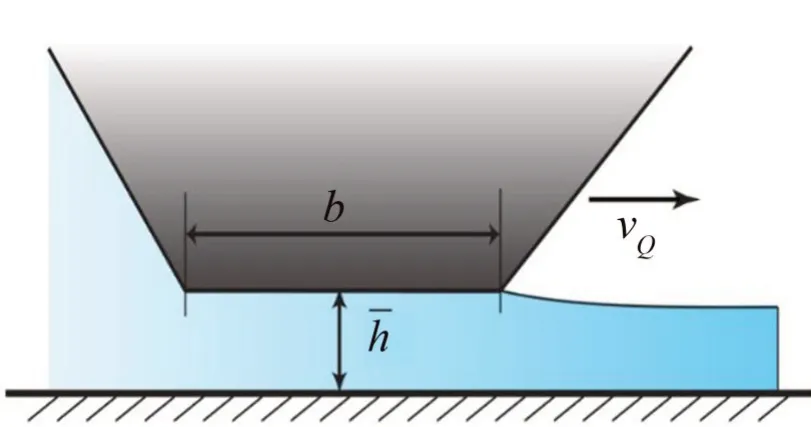
图3 湿润状态下雨刮片-风窗的接触情况

由于作用在汽车风窗玻璃表面的黏性力与雨刮臂作用于雨刮片所施加的外部压力符合库埃特流的特性[17]，因此设定接触面水层的流动为库埃特流动；水层表面产生的接触摩擦力为流体力。

流体摩擦力可以描述为：

湿润状态下摩擦力的无量纲表达式为：

由公式（9）、式（10）、式（12）、式（24）可得：

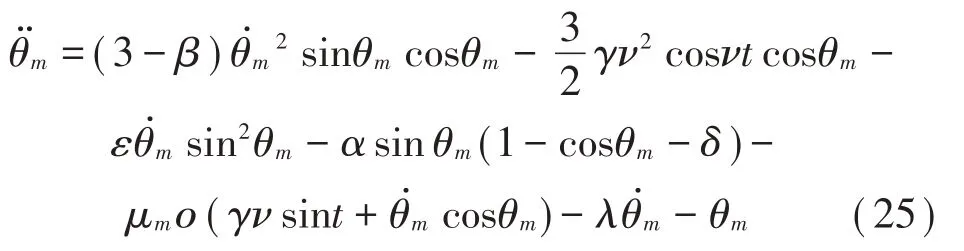
湿润状态摩擦力的时域无量纲表达形式：

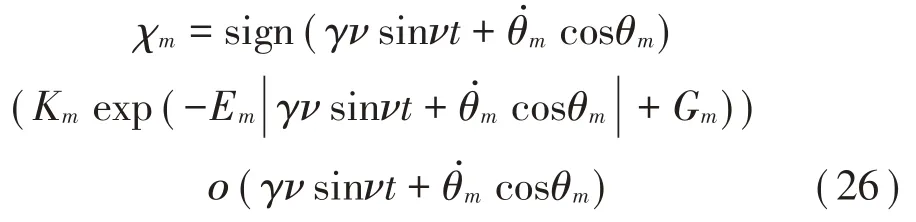
3 数值解与讨论

本节采用龙格-库塔（Runge-Kutta）法[18-19]对无量纲控制方程求解，分析雨刮片的角度变化情况及摩擦系数、摩擦力时域特性。

3.1 动力学分析与振动

利用龙格-库塔法对公式（21）、式（25）进行数值求解，分别获得干燥及湿润工况下雨刮片角度随时间的变化情况，如图4至图5所示。

在t=0时刻，部分初始值设置如下：

其中，角度初始值与实际刮水器叶片的角度一致；为了控制变量，干湿工况下的角度初始值及变量δ的值均相同。

如图4（a）、图5（a）所示为雨刮片角度随无量纲时间在两个刮刷周期内的变化情况，其正负表示雨刮片刮刷过程中的角度方向；角度发生正负变化时雨刮片发生反转。雨刮片角度的变化可反映雨刮片的振动特性。由图4（a）、图5（a）可知，振动，即两种状态的角度变化都发生在反转之后；且反转后的一定时间内角度波动明显，随后逐渐衰减，直到下一次反转。

如图4（b）及图5（b）所示雨刮片在不同工况下沿一个方向运动时的振动情况。雨刮片反转后角度幅值变化较大，随后趋于稳定，说明雨刮片反转之后均为高频振动，随后衰减为低频振动。干燥工况下，雨刮片反转之后的振动相比湿润工况，更为明显，证明干燥工况下尖叫噪声是反转之后的高频振动产生的[7]。湿润工况下，由于水膜作为摩擦副接触面间润滑介质的存在雨刮片角度变化相对平稳，因此振动幅值和振动噪声较小。

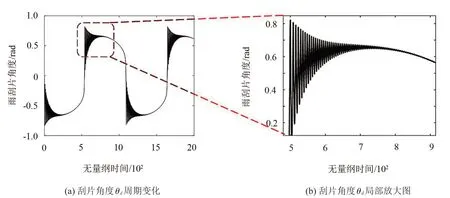
图4 干燥工况θd时域图

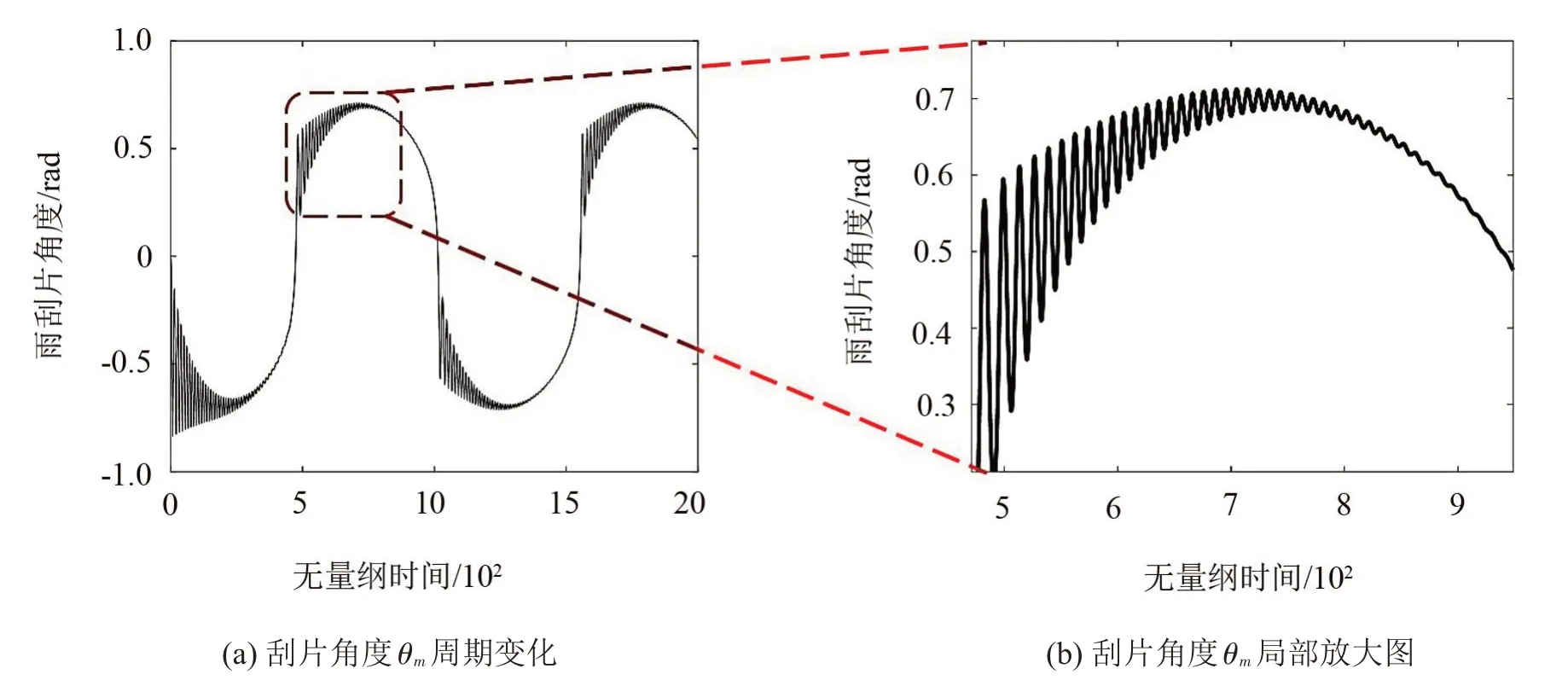
图5 湿润工况雨刮片角度θm时域图

3.2 摩擦系数

根据公式（14）求出摩擦系数-相对速度负斜率的近似曲线如图6所示。其中：K=0.6，E=0.4，G=0.2。

在图6 中实线部分表示动摩擦系数，虚线部分表示静摩擦系数。当vQ*为非零值时，动摩擦系数是斜率为负的单值函数；此时，雨刮处于刮刷过程，且在一定范围内摩擦系数随速度的增大而减小。当vQ*是零值时，静摩擦系数为固定值，即雨刮在反转瞬间为静摩擦，摩擦系数达到最大值，此时摩擦系数的值为μmax=K+G，雨刮在反转瞬间处于静止状态。

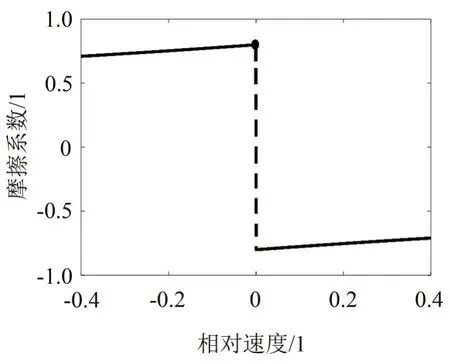
图6 摩擦系数-相对速度负斜率曲线

根据摩擦系数时域曲线，结合公式（17）、式（18），分析干湿工况下的摩擦系数随时间的变化情况如图7至图8所示。

在t=0时刻，部分初始值设置如下：

干燥状态：Kd=0.6Ed=0.4Gd=0.2

湿润状态：Km=0.1Em=0.4Gm=0.1

由图7（a）、图8（a）可知，在两个刮刷周期内速度增加时，摩擦系数减小，当雨刮片的速度达到最大时，摩擦系数最小；速度减小时，摩擦系数增加，在反转时刻，即雨刮片速度减小为0时，摩擦中的由动摩擦转化成静摩擦，摩擦系数达到最大。其中，摩擦系数正负表示雨刮刮刷过程中的方向变化。

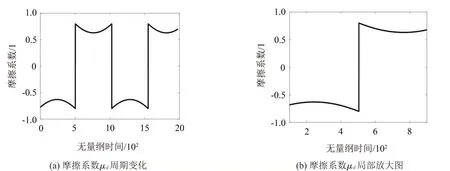
图7 干燥工况摩擦系数μd时域图

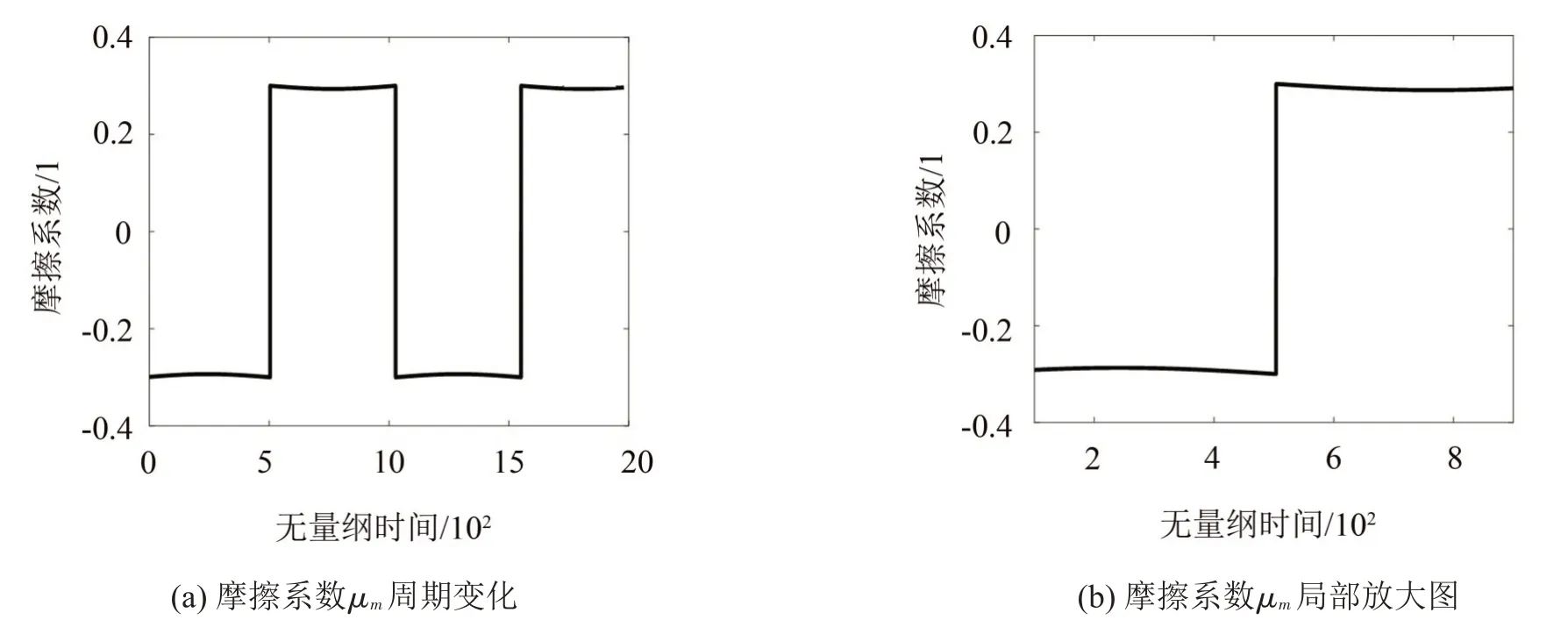
图8 湿润工况摩擦系数μm时域图

两种工况下的摩擦系数也存在一定差异。相比干燥工况，湿润工况下摩擦系数受速度的影响较小；湿润工况下的摩擦系数小于干燥工况，这是由于湿润工况下，接触面间存在润滑介质（水膜）。

雨刮-风窗系统在干湿工况下的周期性摩擦系数时域变化曲线，相对于单值摩擦系数，可更好反映摩擦系数在雨刮片运动中的变化情况。

3.3 摩擦力分析

根据公式（21）、式（25），研究不同干湿工况下的摩擦力随雨刮周期运动的变化情况如图9至图10所示，其中，纵轴为无量纲摩擦力，横轴为雨刮的刮刷时间，摩擦力正负同样代表刮刷方向的改变。

由图9（b）、图10（b）可知，摩擦力幅值在反转后波动较大，折返冲击力较为明显，随后在平扫过程中波动较小，并逐渐趋于稳定，分别与图4、图5 趋势相符，证明雨刮片在反转之后产生的振动与摩擦力相关。

由图9（d）可知，雨刮片反转前的极短时间内，摩擦力发生突变；此处摩擦由滑动摩擦转变为静摩擦，导致摩擦力发生变化。

图10（c）至图10（d）为湿润工况下雨刮反转前后的局部放大图。相比干燥工况，雨刮片反转前的一段时间内，摩擦力也产生波动。出现这种现象是因为流体力被考虑在雨刮片尖部，且与雨刮片尖部的速度成正比；当雨刮臂方向改变前后，尖部的速度减慢，流体力减小，无法使系统力平衡，导致摩擦力发生变化，产生振动。

对比图9（c）和图10（c）可知，在湿润工况下的摩擦力变化较小，这是由于湿润工况下接触面存在一层水膜即润滑介质，摩擦力受速度影响小；而在干燥工况下，反转时折返冲击力的作用明显。

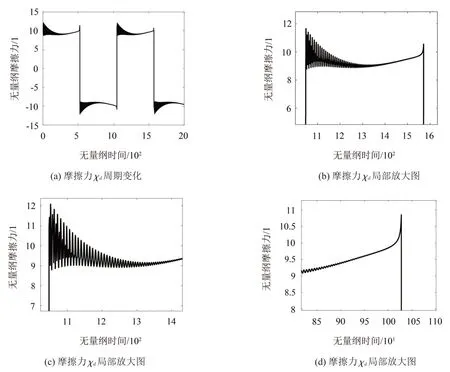
图9 干燥工况摩擦力χd时域图

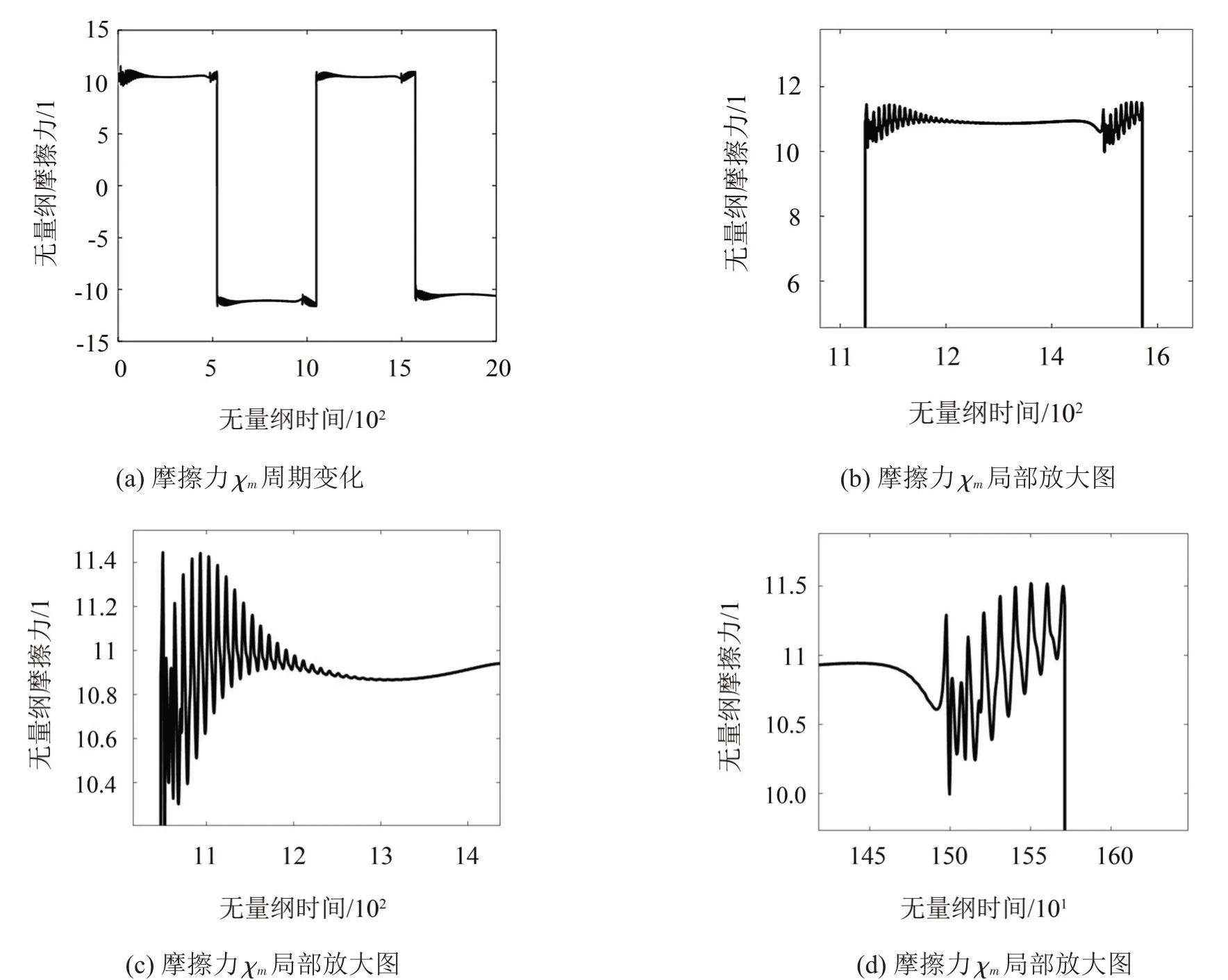
图10 湿润工况摩擦力χm时域

不同干湿工况下，摩擦力及振动的上述变化情况，与文献实验现象较一致[7]，说明第2 节建立的雨刮-风窗系统摩擦力模型具有一定适用性。

4 结语

本文建立了不同工况下的雨刮-风窗系统摩擦模型，研究了干燥及湿润工况下刮片尖部、摩擦系数

及摩擦力在雨刮运行中的变化情况。利用摩擦系数-相对速度负斜率公式，推导出摩擦系数随时间变化的解析式，代替了传统的单值摩擦系数；基于库伦摩擦和库埃特流，求出干湿工况下雨刮片角度及摩擦力随时间变化的解析式；采用龙格-库塔法（Runge-Kutta），模拟了雨刮不同工况下产生的振动以及反转时静止情况；通过不同工况下的仿真结果及结果与文献实验现象对比，验证了摩擦系统动力学模型及摩擦模型的有效性。本文建立的雨刮-风窗系统的摩擦模型，从理论上研究了雨刮片的摩擦和振动特性，为雨刮片结构优化和雨刮-风窗系统振动噪声控制提供一定的理论指导。