重载铁路桥墩基础冲刷对车-轨-桥系统动力响应影响
2022-10-21黄群杰梁展维余翠英
陈 松,龚 凯,黄群杰,梁展维,王 成,余翠英
(1.江西交通职业技术学院建筑工程系,南昌 330013;2.华东交通大学铁路环境振动与噪声教育部工程研究中心,南昌 330013;3.华东交通大学理学院,南昌 330013)
随着重载铁路快速发展,大量跨河跨江的铁路桥梁处于长期服役阶段,河水对铁路桥梁基础的冲刷影响难以避免,这主要表现为桥墩基础周围土体流失、基础埋深减小,引起桥墩基础支撑刚度降低,影响列车行车状态,甚至发生桥梁倒塌事故[1-2]。
为研究桥墩基础冲刷机理及其对桥梁服役状态的影响。Chen等[3]针对斜拉桥主梁及局部桥墩开展了模态频率测试,建立了有限元模型,提出了基于模态频率识别的桥墩冲刷深度评价方法。Fitzgerald等[4]通过现场实测及车桥动力响应分析,提出了基于列车车辆构架加速度的桥墩基础冲刷状态检测方法;Ju[5]建立了考虑土-流体-结构相互作用影响的桥梁有限元模型,分析了考虑流固耦合与不考虑流固耦合对梁体自振频率的影响,提出采用土-结构相互作用模型也能较好地分析自振频率,并得出自振频率随冲刷深度增加而减小;Zampieri等[6]针对欧洲多跨拱桥因洪水冲刷引起的桥梁结构损坏问题,开展了调查,并模拟了冲刷条件下拱桥结构性能的演化过程;Prendergast 等[7]建立了车辆-桥梁-土体相互作用模型,分析了不同土体状态下冲刷对桥梁固有频率的影响;姚锦宝等[8]以城鸡线某桥墩为例,通过开挖桥墩基础周围覆盖层土体的不同厚度模拟基础受冲刷程度,采用冲击振动试验法进行桥墩自振特性测试,分析了桥梁基础受冲刷对桥墩自振特性的影响;贾承岳等[9-11]采用瞬时激励法,开展了三跨简支桥动力模型试验,研究了简支桥中同跨下两墩不均匀冲刷时简支桥自振特性的变化规律;李克冰等[1]采用m法在承台底施加弹簧约束模拟群桩基础等效刚度,计算了基础在不同冲刷深度下车桥动力响应,提出基础冲刷后等效刚度减小,车桥系统横向动力响应增大显著;陈树礼等[12]针对洪水引起的桥墩基础冲刷问题,分析了不同冲刷深度对桥梁自振特性及动力响应的影响,提出了“增补桩基法+增大基础法”的加固措施。可是,关于基础冲刷对重载铁路服役安全的影响研究较少。
为此,基于货物列车-轨道-桥梁系统(Freight Train-Track-Bridge System,简称“FTTB 系统”)空间振动计算模型[13],根据《铁路桥涵地基和基础设计规范》中的m法[14],计算基础冲刷前后等效刚度并开发计算软件,建立基础冲刷条件下FTTB 系统空间振动计算模型,计算并分析不同车速下基础冲刷深度对FTTB 系统响应的影响,为重载铁路服役安全及桥墩基础的养护维修提供参考。
1 基础冲刷作用下FTTB系统空间振动计算模型
1.1 FTTB系统空间振动计算模型
FTTB系统是由货物列车、轨道及桥梁组成的动力耦合系统。设t时刻,一列由1 辆机车+M辆货车组成的列车运行在长度为L的轨道上。列车按照机车或车辆数划分为M+1个车辆单元,每个车辆单元离散为具有26个自由度的多刚体系统,其中,车体、前转向架及后转向架分别考虑3 个平动和3 个转动自由度,每个轮对分别考虑横摆、沉浮2 个自由度,车辆单元的位移如式(1)所示:
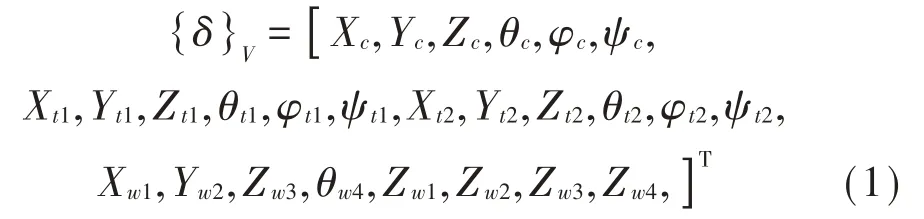
式(1)中:Xc,Yc,Zc,θc,φc,ψc分别为车体纵向、横摆、浮沉、侧滚、点头、摇头位移;Xt1,Yt1,Zt1,θt1,φt1分别为前转向架纵向、横摆、浮沉、侧滚、点头、摇头位移;Xt2,Yt2,Zt2,θt2,φt2,ψt2分别为后转向架纵向、横摆、浮沉、侧滚、点头、摇头位移;Xw1,Yw2,Zw3,θw4为各轮对横向位移;Zw1,Zw2,Zw3,Zw4为各轮对竖向位移。
对于重载铁路桥梁,钢轨、轨枕和梁体均采用梁单元模拟,扣件、道砟均采用线性弹簧及黏滞阻尼器模拟,其横向、竖向弹性系数分别为K1、K2,K4、K5,横向、竖向阻尼系数分别为C1、C2,C4、C5;与支座对应的弹簧系数和阻尼系数分别为K6、K7和C6、C7。轨道-桥梁系统空间振动计算模型如图1所示。
基于上述假定,以相邻横隔板为间距沿梁跨方向将梁跨划分为n个梁段单元。每个梁段单元均离散为具有50个自由度的有限元模型,梁段单元的位移模式如式(2)所示。
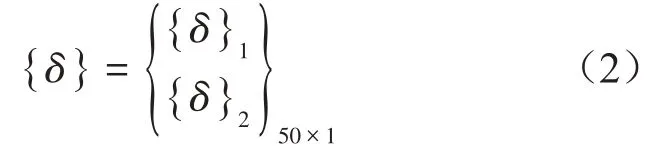
式中:1、2分别表示梁段单元的左端和右端节点;
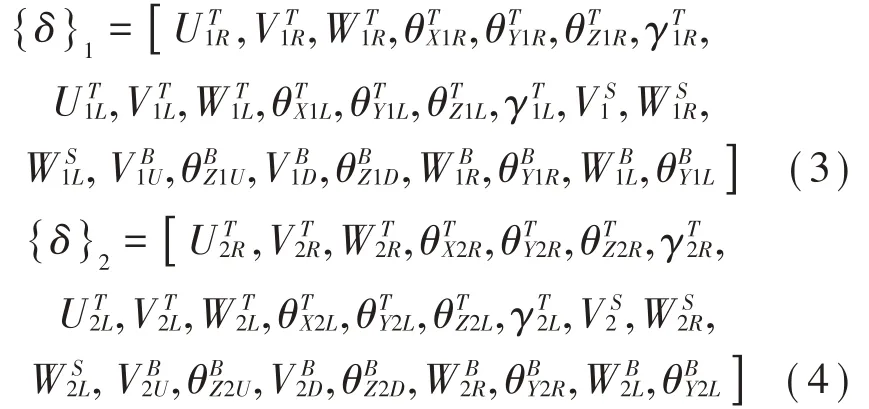
式(3)、式(4)中,上标T、S、B分别表示钢轨、轨枕、桥梁主梁的位移;下标R、L表示梁段单元的右侧和左侧;U、V、W、θ分别为沿桥跨X、Y、Z方向的线位移和转角位移;γ为钢轨沿线路纵向扭转角的变化率;下标U、D分别表示桥梁主梁的上翼缘和下翼缘,下标X、Y、Z分别为梁跨方向(纵向)、垂直于梁跨的水平方向(横向)、垂直于梁跨的竖直方向(竖向)。
此外,桥墩采用梁单元模拟,桥墩基础采用线性弹簧模拟,横向、竖向的弹性系数分别为K8、K9,根据桥墩个数及截面特性划分为P个墩段单元。墩段单元的位移模式如式(5)所示。
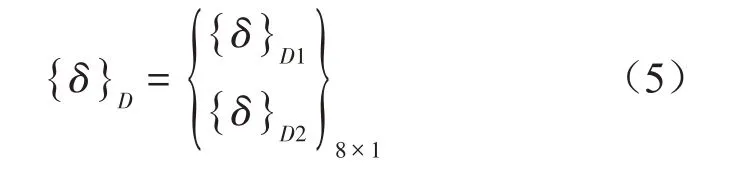
式(5)中,1、2分别表示墩段单元的左端和右端节点:
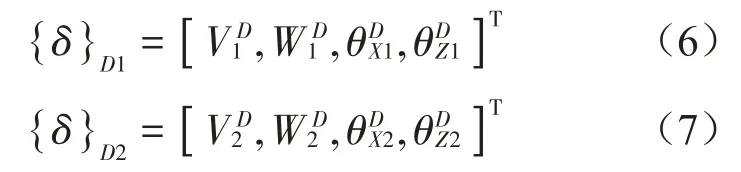
式(6)、式(7)中:上标D表示墩段单元位移,V、W、θ分别表示墩段单元的Y、Z方向的线位移和角位移。
根据上述位移模式,可分别导出车辆单元、梁段单元和墩段单元的空间振动势能为ΠVi、ΠTBj、ΠPk[13,15],再根据车辆单元数、梁段单元数和墩段单元数,将每个单元的势能进行叠加可分别导出列车、轨道-桥梁系统空间振动势能[13,15]如式(8)、式(9)所示。
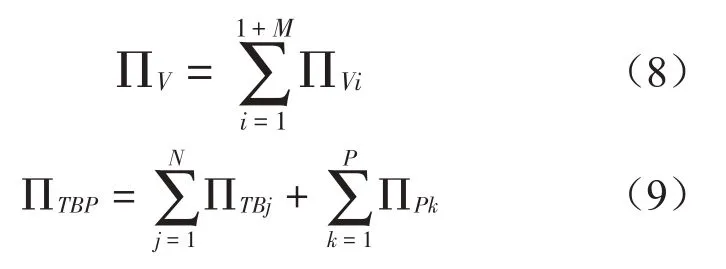
轮轨衔接条件是列车与轨道-桥梁系统的连接纽带。为反映轮轨相对运动状态,采用轮轨相对位移衔接条件作为纽带,如式(10)、式(11)所示。
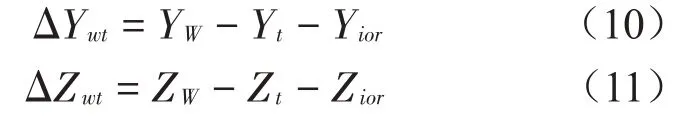
式(10)~式(11)中:ΔYwt、ΔZwt分别为轮轨横向、竖向相对位移;YW、ZW分别为车轮横向、竖向位移;Yt、Zt分别为钢轨横向、竖向位移;Yior、Zior分别为钢轨横向、竖向几何不平顺,并考虑轮轨“游间”影响。
这样,可导出FTTB 系统空间振动总势能如式(12)所示。

按照弹性系统动力学总势能不变值原理[16]对式(12)变分,如式(13)所示:

采用形成系统矩阵方程的“对号入座”法则[17],得到t时刻FTTB 系统空间振动矩阵方程如式(14)所示:
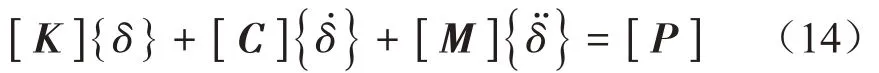
式中:[K]、[C]、[M]、{P}分别为FTTB系统的刚度、阻尼、质量矩阵及荷载列阵。分别为FTTB系统的各自由度位移、速度及加速度列阵。采用构架蛇行波和轨道竖向几何不平顺作为FTTB系统横向、竖向激振源,采用Wilson-θ逐步积分法求解式(14),编制计算程序,得到FTTB 系统空间振动响应。
1.2 基础冲刷模拟
基础冲刷表现为基础周围土体埋深减小,桥墩基础支撑状态改变。为反映桥墩基础支撑状态,采用等效刚度模拟,如图1 所示,基础横向、竖向等效刚度分别为K8和K9。这里,采用m 法计算等效刚度,计算过程详见文献《铁路桥涵地基和基础设计规范》[14]。以慈河特大桥为例[18],墩高2.5 m,桥墩横截面为圆端形,截面尺寸见文献[18];桩基础为摩擦桩,基础埋深土层为粗砂和卵石土,地基比例系数m=6 kP/m2×104kP/m2,内摩擦角φ=40°,承台底面高于局部冲刷线,桩入土深度为15 m,桩身直径为0.8 m,采用C20 混凝土(弹性模量E=2.55×107kN/m2)桩基础中心间距为2.2 m,桥墩桩基础截面尺寸如图2所示。
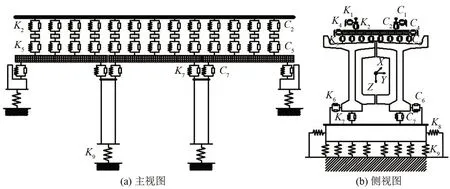
图1 轨道-桥梁系统空间振动计算模型
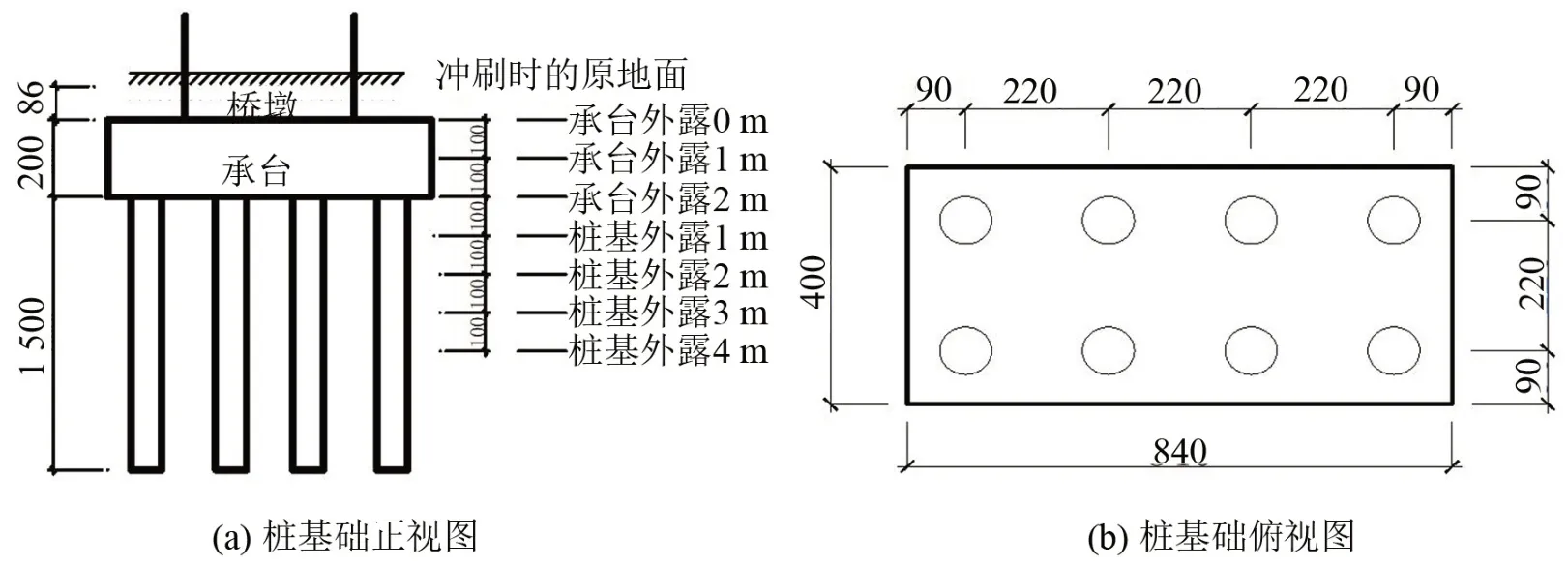
图2 桥墩桩基础截面尺寸(单位:cm)
为使桥墩基础等效刚度计算简便,编制了相应的计算软件。软件中设置了基础参数、基础类型及计算结果三个模块,其中,基础参数包括桩基直径、冲刷深度、桩数、埋深深度、桩间距、土摩擦角度;基础类型包括桥墩截面形状、地基土类型、桩基础类型;计算结果包括桥墩墩底横向、竖向刚度(即第1.1节中的K8和K9)。采用编制的计算软件,分别计算了桩基外露0(即承台外露2 m处)、2 m、4 m时的横向及竖向等效刚度如表1所示。由表1表明,不同冲刷深度条件下桩基础横向、竖向等效刚度与文献[18]结果基本吻合,表明软件可靠。同时,随着冲刷深度的增大,基础横向刚度衰减显著,而竖向刚度变化不大。

表1 不同冲刷条件下桥墩基础等效刚度
1.3 模型验证
为验证模型的可靠性,以文献[18]中的计算工况为例。列车编组为1 辆机车加16 辆敞车,计算车速为50 km/h。选取7 跨32.0 m 预应力混凝土简支梁单线桥作为计算对象,直线桥,梁型为参标桥2019,桥墩及基础结构与1.2 节一致。通过计算,得到桩基外露2 m 时桥墩墩顶横向振幅为0.24 mm。而文献[18]中的计算值和实测值分别为0.19 和0.25 mm。可见,计算模型是可靠的。此外,限于篇幅,这里列出了脱轨系数Q/P、轮重减载率ΔP/P、梁体跨中横向位移Bh、墩顶横向位移Dh等时程曲线如图3 至图6所示。
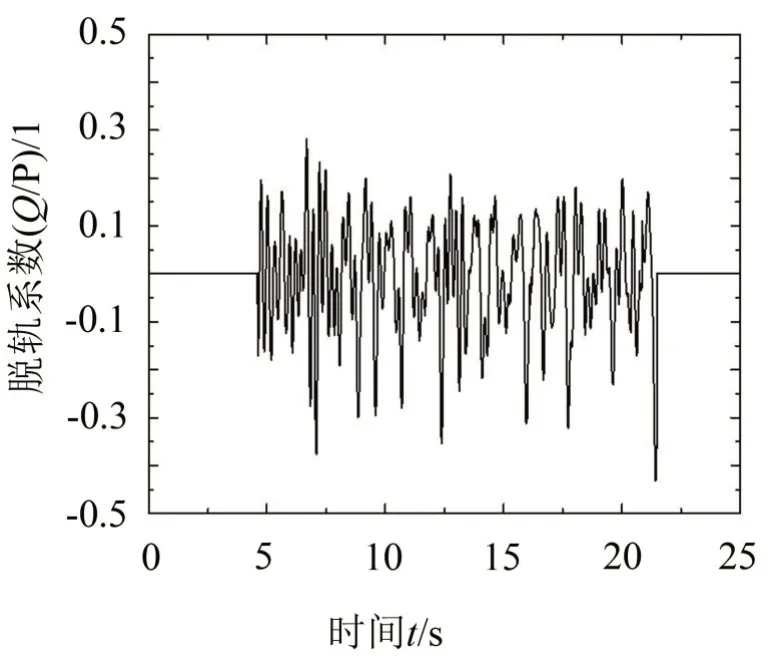
图3 Q/P时程曲线
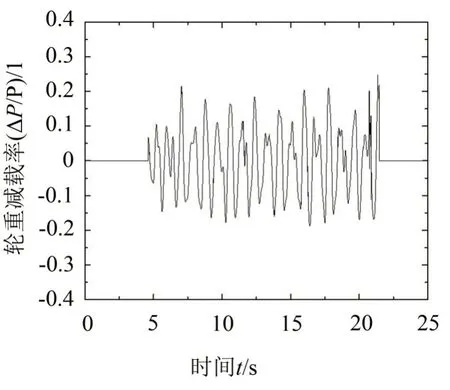
图4 ΔP/P时程曲线
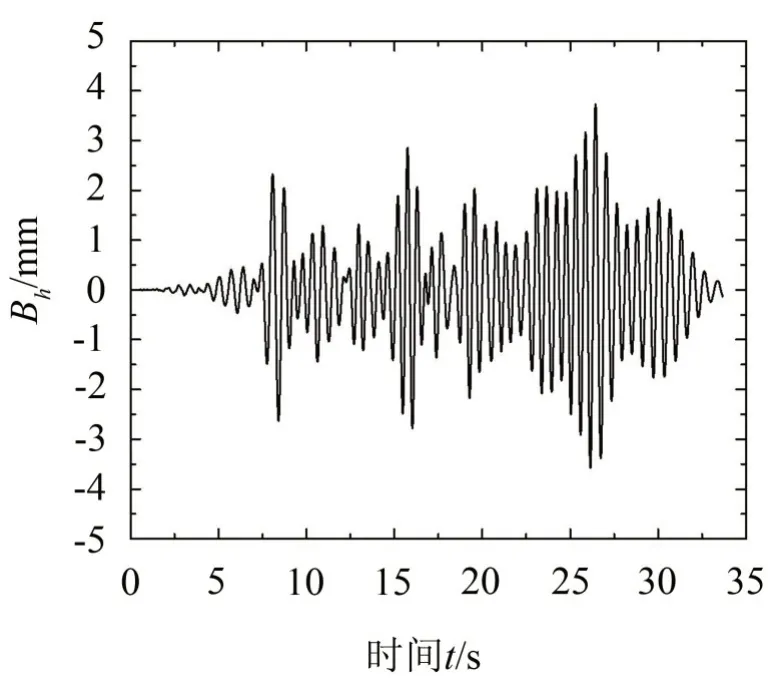
图5 Bh时程曲线

图6 Dh时程曲线
2 不同车速下基础冲刷对FTTB 系统振动响应的影响
本节分析不同车速下基础冲刷对FTTB 系统振动响应的影响。取计算车速V=60 km/h~80 km/h,列车编组、轨道及桥梁结构、基础冲刷作用与第1节一致。计算得到FTTB系统空间振动响应,Q/P、ΔP/P、Bh、Dh等随V及冲刷深度的变化如图7 至图10所示。
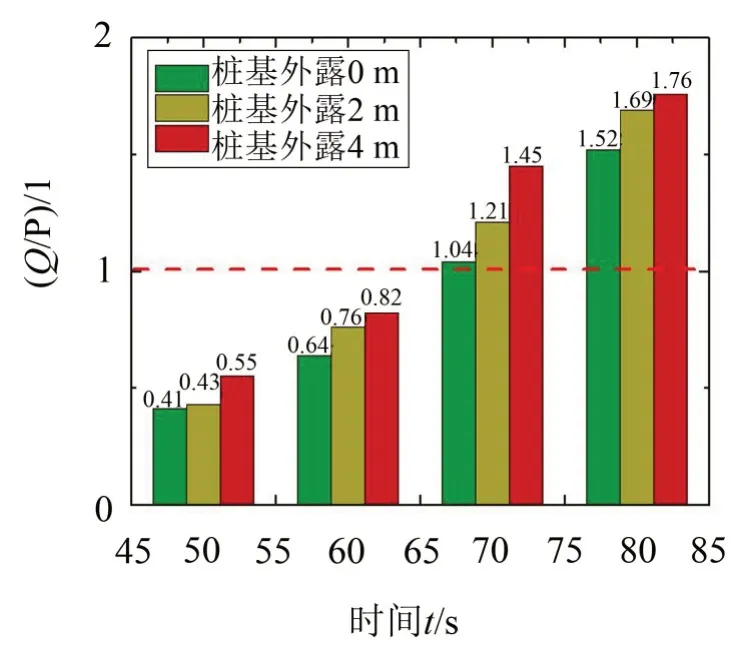
图7 Q/P随V及冲刷深度的变化
图7 表明,随着V及冲刷深度增大,Q/P逐渐增大,其中,当V≤60 km/h且桩基外露0、2 m、4 m时Q/P均未超过规范限值1.0[19];当V≥70 km/h 且桩基外露0、2 m、4 m时Q/P均超过规范限值1.0。可见,车速≥70 km/h且冲刷外露至桩基后列车行车不安全。
图8表明,当V≤60 km/h时所有冲刷深度下ΔP/P均未超过规范限值0.65[19];当V≥70 km/h且桩基外露0 m时ΔP/P接近规范限值0.65,而桩基外露2 m、4 m时ΔP/P超过规范限值0.65。可见,车速≥70 km/h且冲刷外露至桩基后列车车轮减载程度增大。
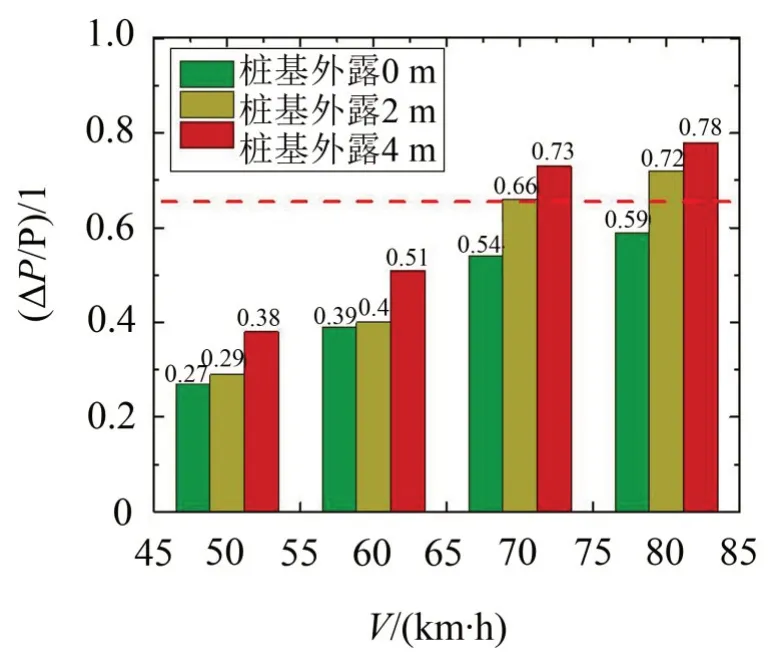
图8 ΔP/P随V及冲刷深度的变化
图9表明,当V≤60 km/h且桩基外露0、2 m时Bh均未超过规范限值3.56[20];当V=70 km/h且桩基外露2 m、4 m 时Bh均超过规范限值3.56[20];当V=80 km/h且桩基外露0 m、2 m、4 m 时Bh均超过规范限值3.56[20]。此外,各车速下桩基外露4 m时的Bh接近或超过规范限值3.56 mm[20]。由此可知,车速≥70 km/h时桩基冲刷直接引起梁体跨中横向位移超限,尤其是桩基外露4 m对梁体跨中横向位移影响显著。
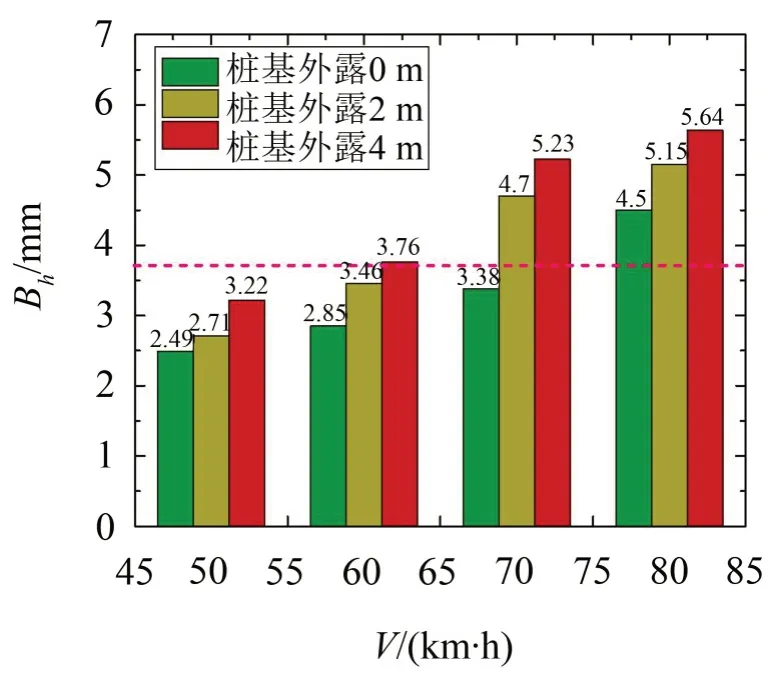
图9 Bh随V及冲刷深度的变化
由图10 表明,随着V及冲刷深度增大,Dh逐渐增大,其中,当V≤60 km/h且桩基外露0、2 m时Dh均未超过规范限值0.5 mm[20];当V≥70 km/h 且桩基外露2 m、4 m时Dh显著增大,接近或超过规范限值0.5 mm[20]。由此表明,当V≥70 km/h时,桩基外露2 m时建议进行加固。
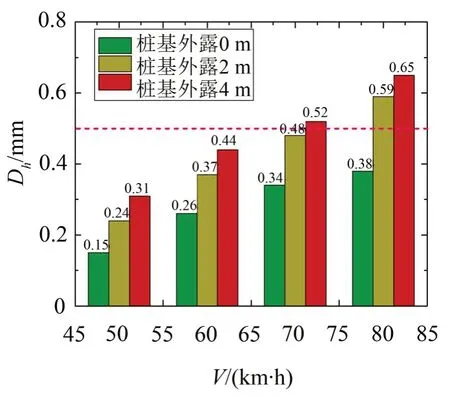
图10 Dh随V及冲刷深度的变化
3 结语
基于FTTB 空间振动计算模型,采用等效刚度模拟桥墩基础冲刷,建立了基础冲刷条件下FTTB系统空间振动计算模型,分析了不同车速下基础冲刷对FTTB 系统振动响应的影响。得出了以下结论:
(1)通过分析得到模型计算结果与文献结果基本一致,验证了模型的合理性,并开发了桥墩基础等效刚度的计算软件。
(2)随着车速及基础冲刷深度的增大,脱轨系数及轮重减载率增大,其中,车速≥70 km/h且冲刷外露至桩基时轮重减载幅度增大,建议适当减速。
(3)随着车速及基础冲刷深度的增大,梁体跨中及墩顶横向振幅增大,其中,桩基外露2 m后对梁体跨中及墩顶横向振幅影响显著,建议对桥墩基础进行加固。
