轴承耦合故障的多步网格搜索优化稀疏诊断方法

巩晓赟 李 超 赵志伟 宁小鹁 张玉祥 韩 明

（1 郑州轻工业大学 机电工程学院， 河南 郑州 450002）

（2 河南中烟工业有限责任公司 安阳卷烟厂， 河南 安阳 455004）

（3 巩义市建设机械制造有限公司， 河南 巩义 451200）

0 引言

转子系统由于工况环境和全工时运转的工作性质，易出现2种甚至3种故障同时存在的情况。转子不平衡故障是航空发动机等旋转机械常见的故障类型之一，在长时间运行过程中产生的持续振动对轴承等零部件易造成损伤，导致不平衡轴承等耦合故障的发生[1-2]。而耦合故障振动信号相较于单一故障振动信号更加复杂，多种故障成分之间相互影响，相互耦合，导致信号中的弱故障特征被强故障特征和强噪声成分所覆盖，信噪比降低，增加了故障诊断的难度[3-5]。

稀疏表示作为一种信号处理方法，由于其稀疏性、高分辨率和强抗干扰能力等优点，在机械故障诊断领域得到了广泛应用[6-8]。Tang等[9]提出了一种基于稀疏表示的潜在分量分解方法，实现了强噪声背景下轴承与齿轮弱故障特征的有效识别。樊薇等[10]提出基于小波基的稀疏信号特征提取方法，利用相关滤波法构建最优小波冗余基底，并运用优化最小算法转换信号的瞬态冲击成分，实现了强噪声背景下弱特征的有效提取。吴芳坦等[11]则采用具有提升总体目标凸函数稀疏性的重叠群稀疏算法，从相关信号中提取并重构出齿轮局部冲击故障信号。

稀疏表示将信号表示成少量原子的线性组合，实现信号的稀疏性表达，可有效匹配信号中具有周期结构特征的优质信号[12]。但是，稀疏表示的性能依赖于过完备字典参数的选择，基于经验值的参数设置因参数的复杂多样和取值范围广，无法直接得到参数最优值[13]。本文中通过多步网格搜索法的交叉验证思想优化稀疏表示参数，降低位移因子和频率因子对重构误差的影响，提升了耦合故障的稀疏表示性能。首先，以位移因子和频率因子的搜索范围构成网格面，建立多步网格搜索优化稀疏表示方法模型，通过多步网格搜索选取稀疏表示的最优参数；其次，通过最优参数确定基于自适应Gabor原子字典正交匹配追踪的稀疏表征信号；最后，通过轴承实测信号进行基于径向基函数的SVM 的分类与识别，验证了本文中方法的准确性和耦合故障识别的适用性。

1 稀疏表示理论

1.1 稀疏表示

信号稀疏表示能有效提取非线性复杂振动信号中的特征[14]。设长度为p的信号y，可看作Rn的一个向量，过完备字典D=[d1，d2，…，dn]，则信号y可表示为

式中，xi为基函数的系数；x={x1，x2，…，xn}为信号的稀疏矩阵；n＞p。

本文中采用的稀疏表示方法是自适应Gabor原子字典的正交匹配追踪（Orthogonal matching pursuit，OMP）算法[15-16]。计算过程是通过原始信号建立Gabor 原子的过完备字典，利用OMP 算法对原始信号进行匹配计算，寻找过完备字典中最佳匹配原子并生成残余信号，根据残余信号生成新的过完备字典并进行下一次匹配计算，直到残余信号满足条件后终止计算。

Gabor 原子是一种时频原子，具有良好的时频逼近性能，能有效匹配到信号中的循环特征。其基本定义为

式中，g(t) =e-πt2为高斯窗函数；γ=(s，u，ξ)为原子参数。

OMP算法的具体计算过程如下[17]：

输入：过完备字典D，信号y，尺度因子s。

输出：重构的信号x̂。

初始值：残差r0=y，索引集Λ0=D，迭代步数t= 1。

Step1：找到残差r和过完备字典原子dj中内积 最 大值所对应的脚标λ，即λi=arg maxj=1,…,N|＜ri-1，dj＞|。

Step2：更新支撑集Λ=Λt-1∪{λi}，记录到字典中，重建原子集合Di=[Di-1，dλt]。

Step3：由最小二乘法得到x̂=arg min‖ ‖

y-Dtx̂t2，并更新残差rt=y-Dtx̂t。

Step4：若t＜s，t=t+ 1，返回step1；若t=s，则停止迭代，输出重构信号x̂=x̂t。

1.2 参数设置对重构误差的影响

由式（2）中可知，Gabor 原子字典内部函数主要由原子γ=(s，u，ξ)决定，尺度因子s、位移因子u和频率因子ξ不同，对应的重构误差不同[18]。在相同迭代下，各参数值附近10%的变化范围内的重构误差变化如图1所示。

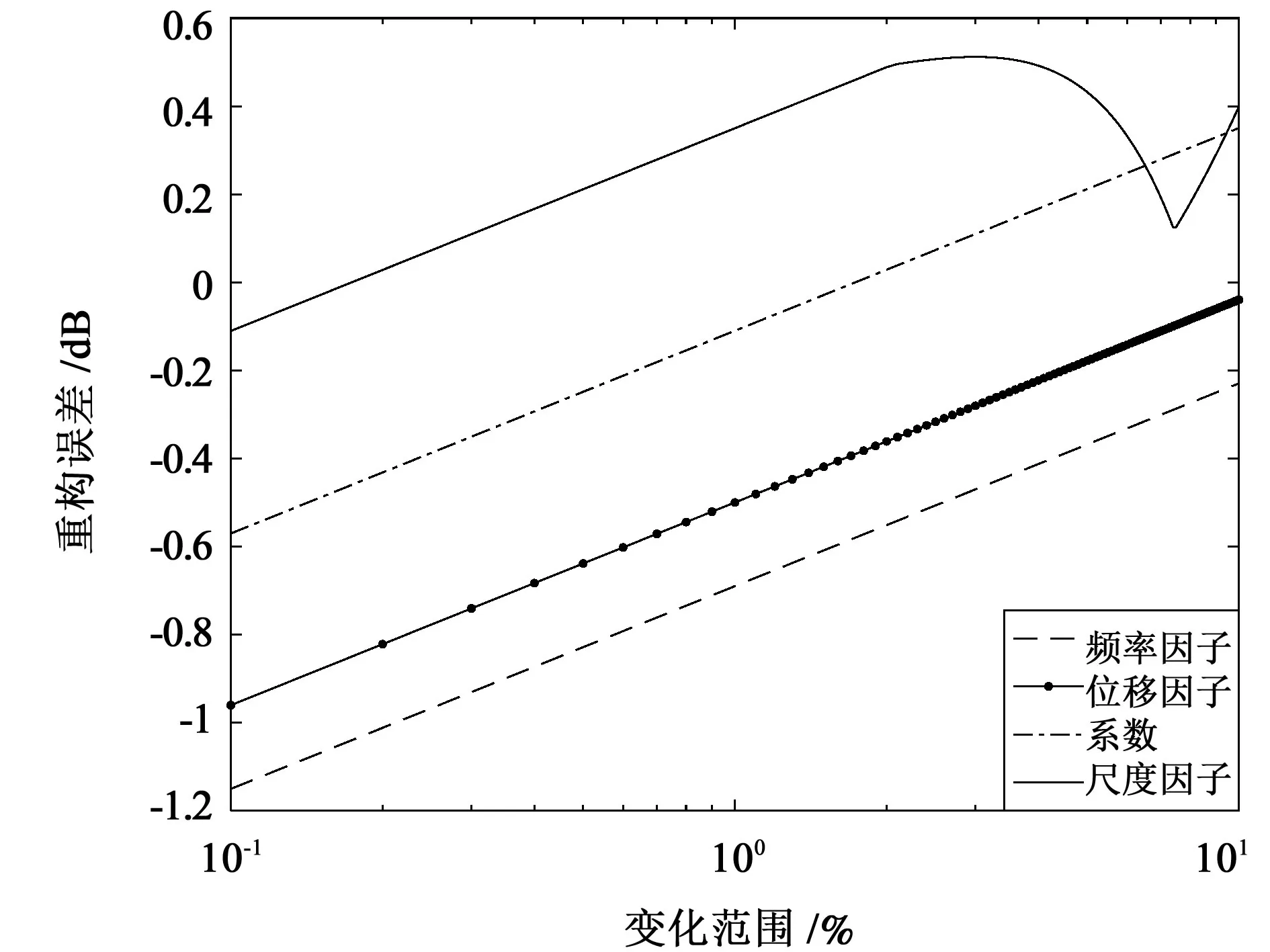
图1 Gabor原子参数对信号重构误差影响Fig.1 Influence of Gabor atomic parameters on signal reconstruction error

将重构误差E作为优化目标，设待分解信号为f，过完备字典D={gy(t) }，则f可以分解为

式中，gγ为原子；R1f为残余信号。残余信号和原子正交，有

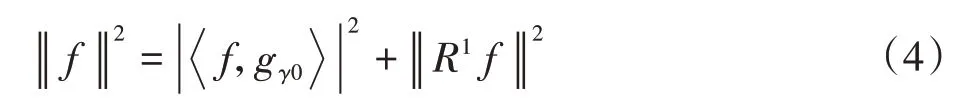
最佳原子gγ n满足

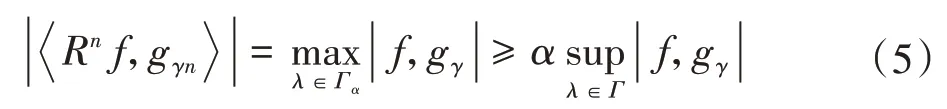
利用已经得到的原子对gγn进行正交运算，得

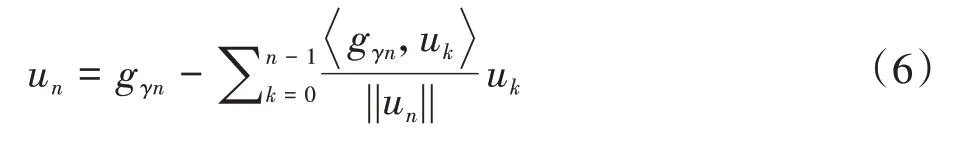
根据式（6），再次计算残余信号为

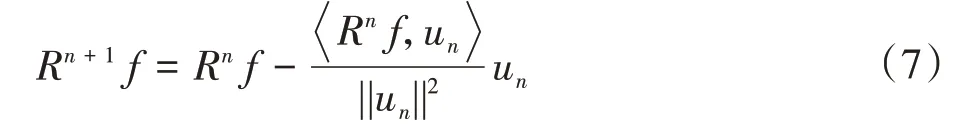
重构误差E是关于Gabor 函数和迭代次数n的函数。第n+ 1次迭代表示为

则，n+ 1次迭代的重构误差为

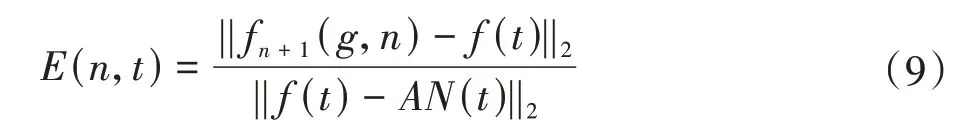
式中，f(t)为待处理的时间信号；AN(t)为待处理信号关于时间t的噪声信号。

2 稀疏表示参数优化模型

为了提高重构精度，本文中针对Gabor原子字典的位移因子u和频率因子ξ进行优化，通过多步网格搜索的迭代选优和OMP算法实现。

根据网格搜索法理论，设搜索空间的坐标系r=(u，ξ，E)。其中，u∈(u1，u2)，ξ∈(ξ1，ξ2)共同构成网格面u-ξ，步长为L，网格点表示为u∈(u1，u1+L，…，u2)，ξ∈(ξ1，ξ1+L，…，ξ2)。取空间坐标系上一点为P，其垂直平面坐标为Q(ui，ξi)，P、Q两点之间距离为dist，对应的重构误差为E(n，t)。传统网格搜索法只进行一次搜索，网格中重构误差最小点的位置即认为是最优参数，此时，距坐标系距离最小为distmin。则

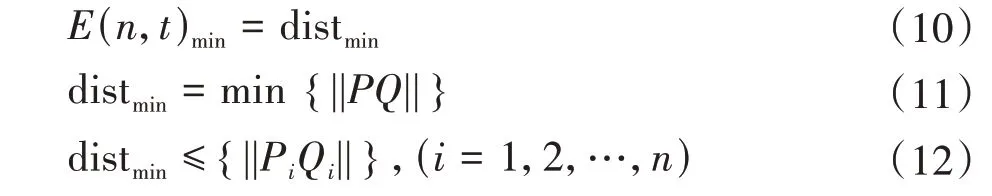
本文中的多步网格搜索法为多次搜索。设初始搜索范围为u∈(u1，u2)，ξ∈(ξ1，ξ2)构成的网格面u-ξ，初始步长为L0，网格点表示为u∈(u1，u1+L0，…，u2)，ξ∈(ξ1，ξ1+L0，…，ξ2)。网格中重构误差最小点P0，即为此次搜索的最优点，其垂直坐标点为Q0，则

再以P0为中心，重新设定搜索区域u1∈(u1，u1+L0)，ξ1∈(ξ1，ξ1+L0)，搜 索 步 长 更 新 为L1=L0/2。新搜索区域的网格点可表示为u1∈(u1，u1+L1，…，u1+L0)，ξ1∈(ξ1，ξ1+L1，…，ξ1+L0)。该区域重构误差最小点为P1，其垂直坐标点为Q1，则

进而，以P1为中心设定搜索范围，重复以上搜索流程，直至满足迭代终止条件L≤α。其中，α是经多次迭代试验而保持重构误差不变的最大值。多步网格搜索优化稀疏表示方法模型如图2所示。

图2 多步网格搜索优化稀疏表示方法模型Fig.2 Multi-step grid search optimization sparse representation model

3 仿真分析与实验验证

3.1 仿真信号分析

为验证多步网格搜索算法优化的稀疏表示模型对转子系统不平衡-轴承耦合故障信号的重构和降噪性能，构建式（15）～式（18），分别仿真轴承正常、单一轴承故障、单一不平衡故障和不平衡-轴承耦合故障。其中，x0表示高斯白噪声。不平衡-轴承耦合故障的仿真信号如图3所示。

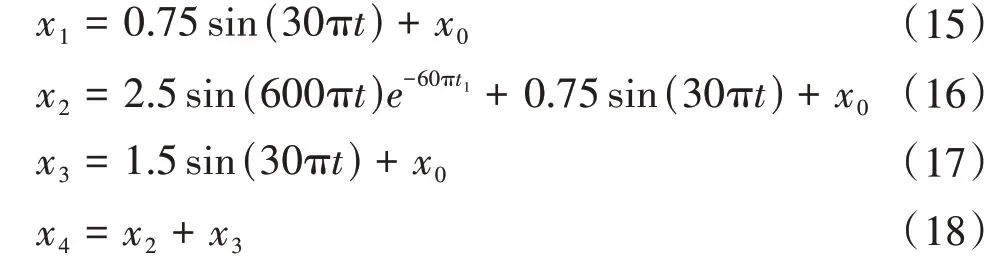
设置多步网格搜索算法中的位移因子u和频率因子ξ初始取值范围为[-10，10]，初始步长为4，步长迭代停止阈值为0.1。组合位移因子u和频率因子ξ两个参数，构成5×5 的u-ξ网格面，计算图3 中耦合故障仿真信号参数节点在稀疏表示下的重构误差E和重构时间T。选择寻优结果中重构误差最小的区域并更新搜索范围和步长，直至满足迭代停止条件。参数计算过程及其参数寻优结果如图4所示。

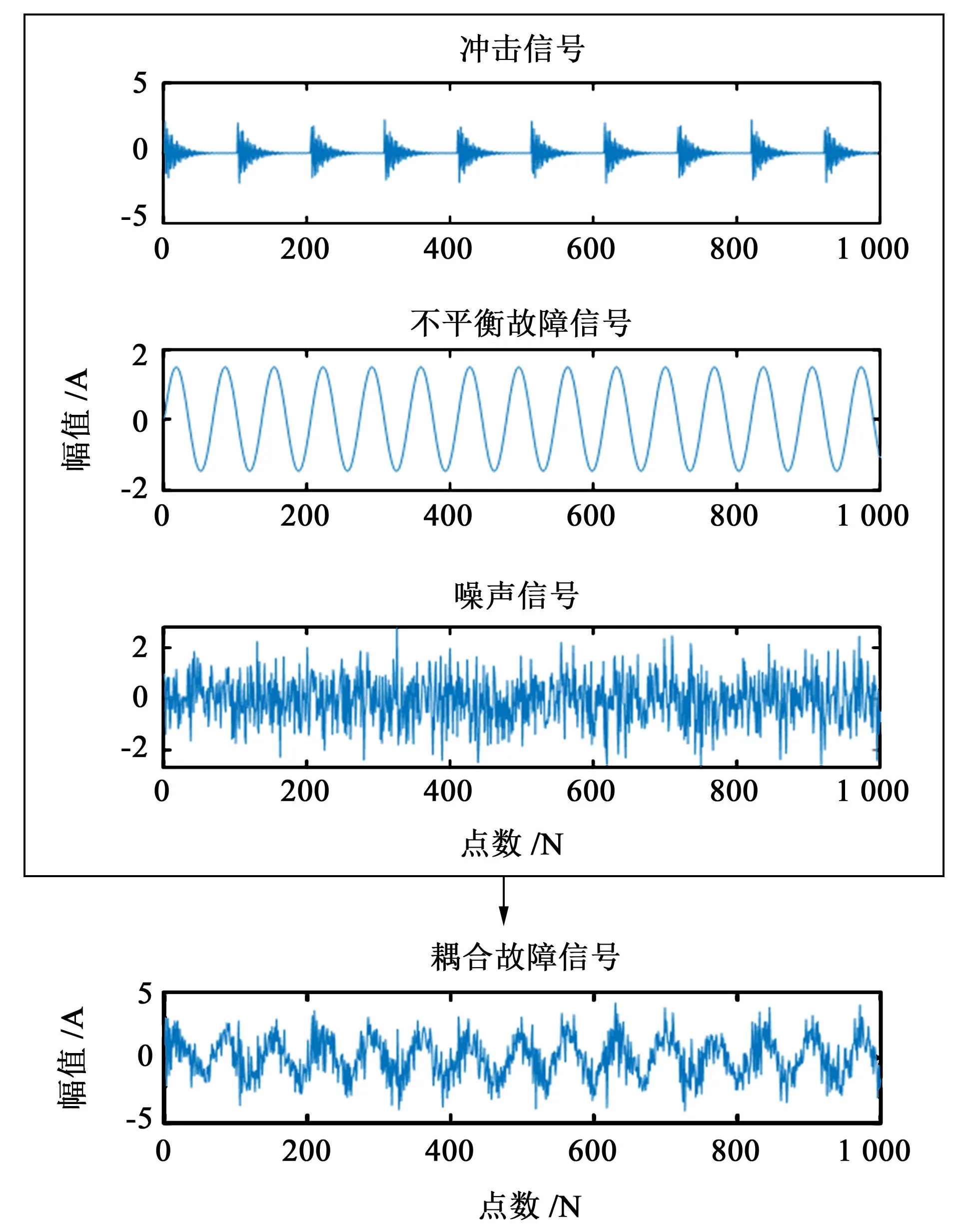
图3 不平衡-轴承耦合故障仿真信号Fig.3 Unbalance-bearing coupling fault simulation signals

由图4 中可知，当位移因子u= 2、频率因子ξ=2 时，最小重构误差E=0.361 2。设定相同的迭代步数，采用本文中方法与未优化参数的稀疏表示方法分别对图3 所示的不平衡-轴承耦合故障仿真信号进行重构，得到如图5所示耦合故障的重构信号与重构时间。对比分析可知，多步网格搜索优化稀疏表示方法能有效提取信号中的循环特征，突出信号的冲击成分，保证了参数优化后稀疏表示的准确性；同时，参数优化后信号重构时间缩短17.84%，提高了稀疏表示运行效率。

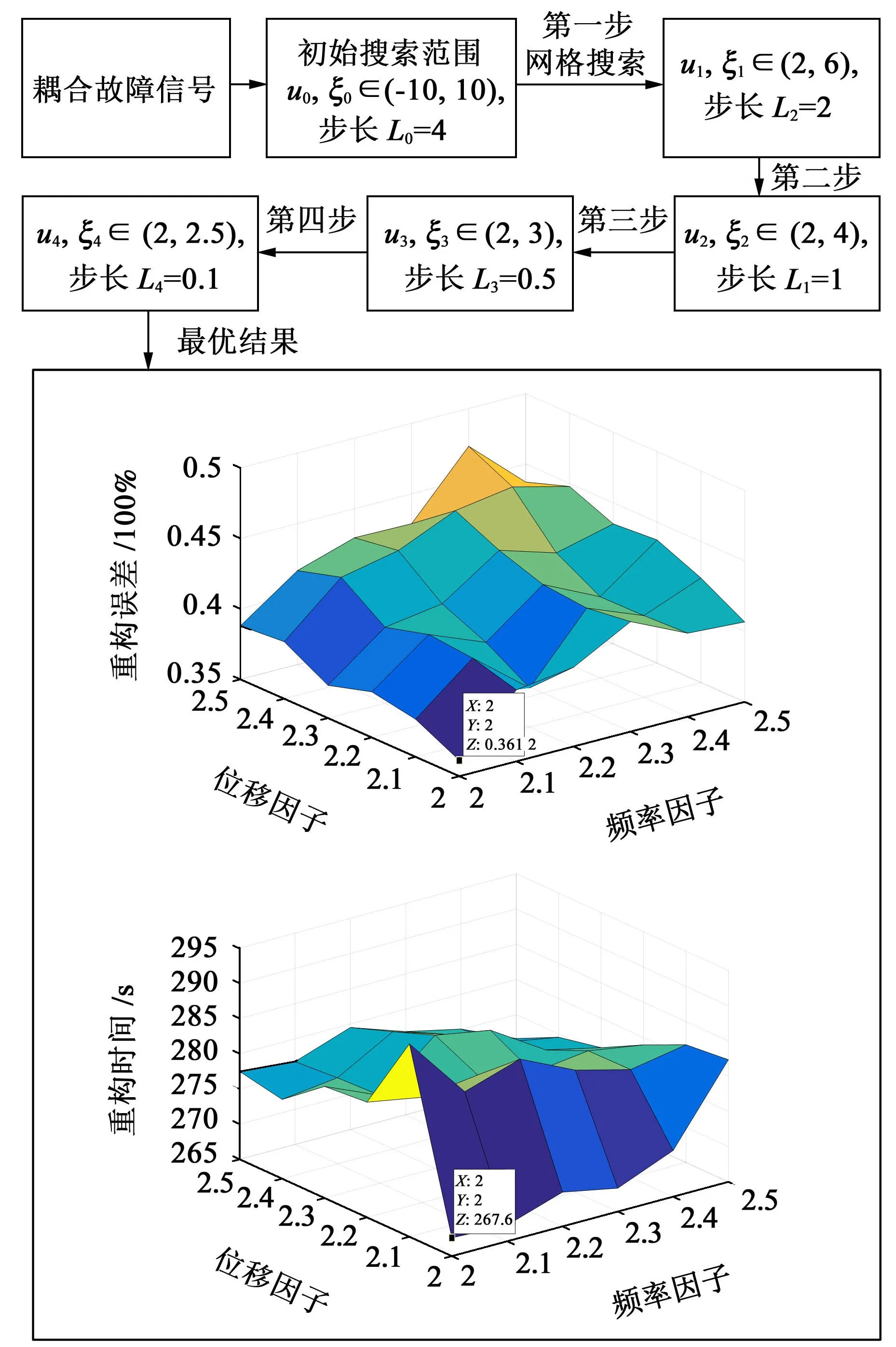
图4 多步搜索流程及最终参数搜索结果Fig.4 Multi-step search process and results of parameter search

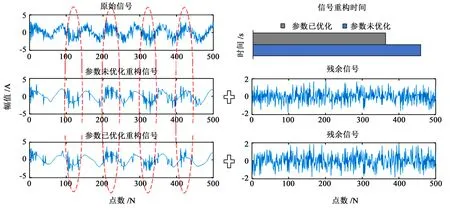
图5 重构结果Fig.5 Reconstruction results

为了进一步验证多步网格搜索优化稀疏表示模型的重构效果，对耦合故障信号加入不同信噪比的噪声信号，并分别计算原始信号、未优化参数和已优化参数稀疏表示重构信号的信噪比，结果如图6所示。由图6（a）中不同噪声环境下信噪比的对比结果可知，当噪声信号大于1 dB 时，本文中方法的信噪比结果大于未优化参数的稀疏表示结果，且噪声干扰越大，多步网格搜索优化稀疏表示模型的重构效果越好。图6（b）是加入5 dB噪声的重构信号波形图，可看出多步网格搜索优化稀疏表示方法的降噪效果得到进一步提升。

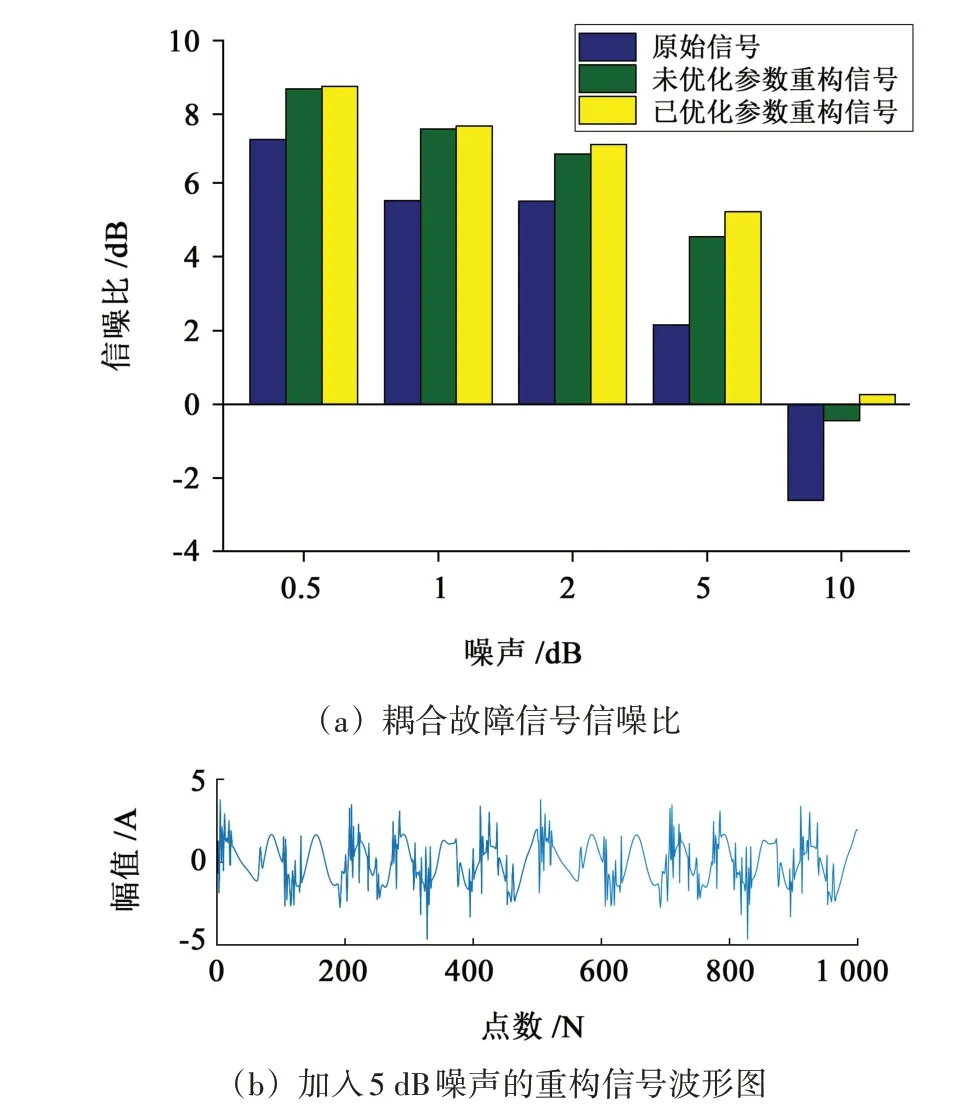
图6 不同噪声下耦合故障的降噪效果Fig.6 Noise reduction effect of coupling faults under different noises

图7 所示为不平衡-轴承耦合故障稀疏表示重构信号的包络谱结果。从图7中可知，采用本文中方法的包络谱结果优于未优化参数的包络谱结果，干扰信号减弱，故障特征增强。

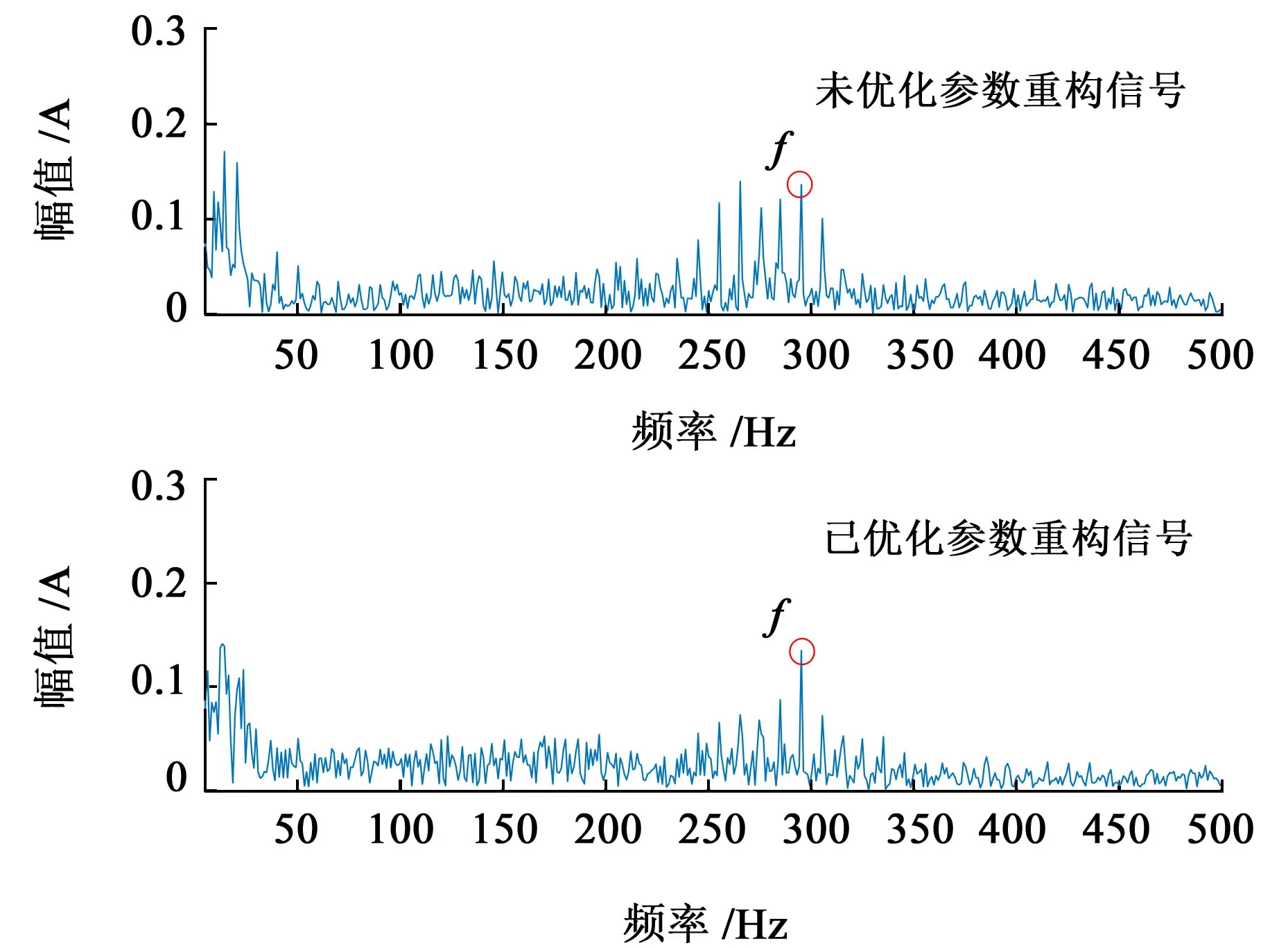
图7 仿真不平衡-轴承耦合故障重构包络谱Fig.7 Envelope spectrum reconstruction for unbalance-bearing coupling fault simulation

3.2 实验分析

采用美国SQ 公司机械故障综合试验台模拟实验数据进行了分析验证，分别模拟了转子不平衡故障、负载端轴承故障、电机端轴承故障以及其相互之间的耦合故障。图8 所示为试验台及其故障设置示意图。其中，负载端轴承型号为ER-12K，电机端轴承型号为6203；转子不平衡质量块为1 个螺钉加两个垫片，不平衡位置为左侧轮盘外圈第7 个孔位。实验中，设置电机转速为1 800 r/min，采样频率为12 800 Hz，振动信号由加速度传感器B所采集。

图8 试验台及其故障设置示意图Fig.8 Diagram of the test bench and its fault setting

利用4 个实验案例对本文中提出的方法进行实验验证，每个案例由4 类不同故障类型的信号组成。表1 所示为4 个实验案例中信号故障类型的详细信息。其中，案例1 的分析基础为4 类轴承与转子不平衡耦合故障的信号；案例2 为转子不平衡与轴承单一故障的信号；案例3、案例4 分别为单一故障和耦合故障相组合的信号。每个实验案例采集240组信号，其中，每类故障信号60 组（训练样本30组，测试样本30 组）。

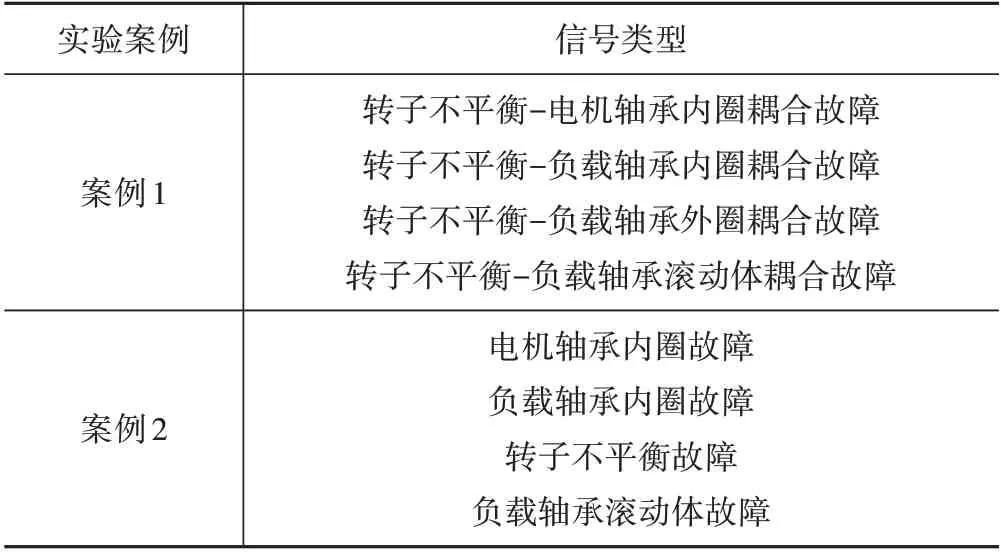
表1 实验案例信号组成Tab.1 Experimental data signal type

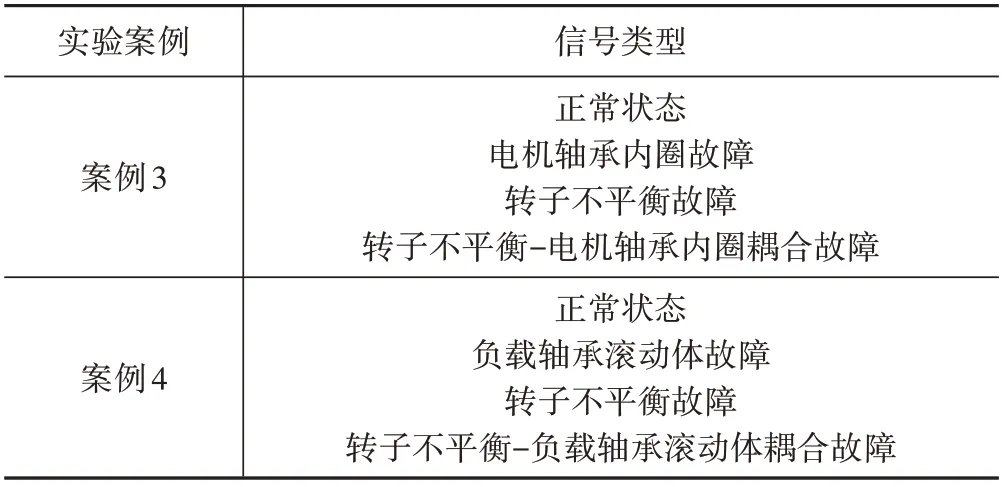
续表

用本文中所提方法对案例1中的耦合故障信号进行实验分析。首先，利用基于多步网格搜索优化模型的稀疏表示方法对案例1 中耦合故障信号进行重构，图9 所示为转子不平衡-负载轴承外圈耦合故障振动信号的重构结果。从图9中可知，本文方法能够有效重构出振动信号的循环特征和冲击成分。

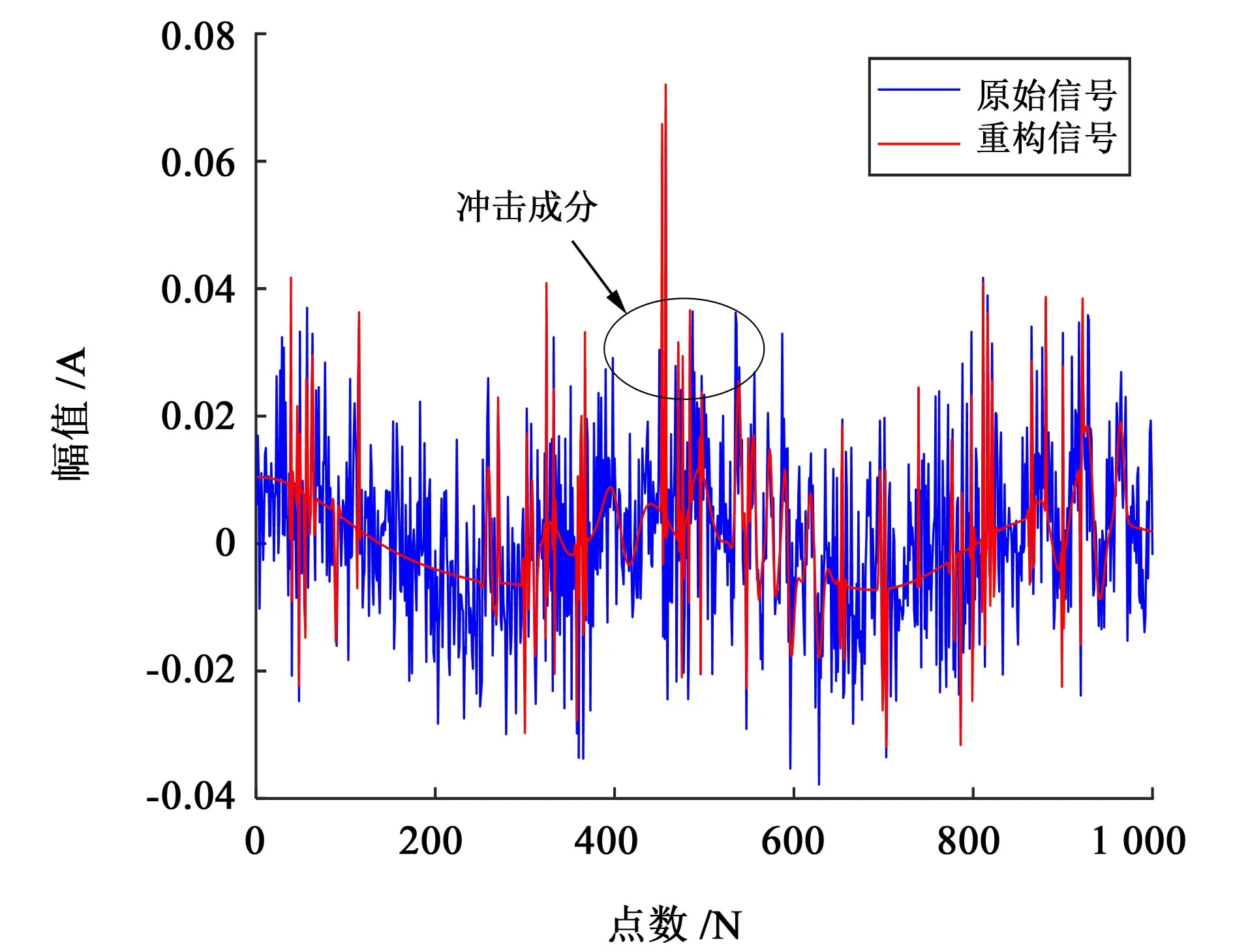
图9 转子不平衡-负载轴承外圈耦合故障重构信号Fig.9 Reconstruction signals of rotor unbalance loaded bearing outer ring coupling faults

其次，计算经本文方法稀疏重构后每组信号的均方根值、频率方差和尺度熵三维特征。再将案例1中每类信号的三维特征向量输入基于径向基函数的SVM 分类模型进行分类。图10 所示为信号优化重构前后的特征空间分布图，图11 所示为信号优化重构前后的分类结果。

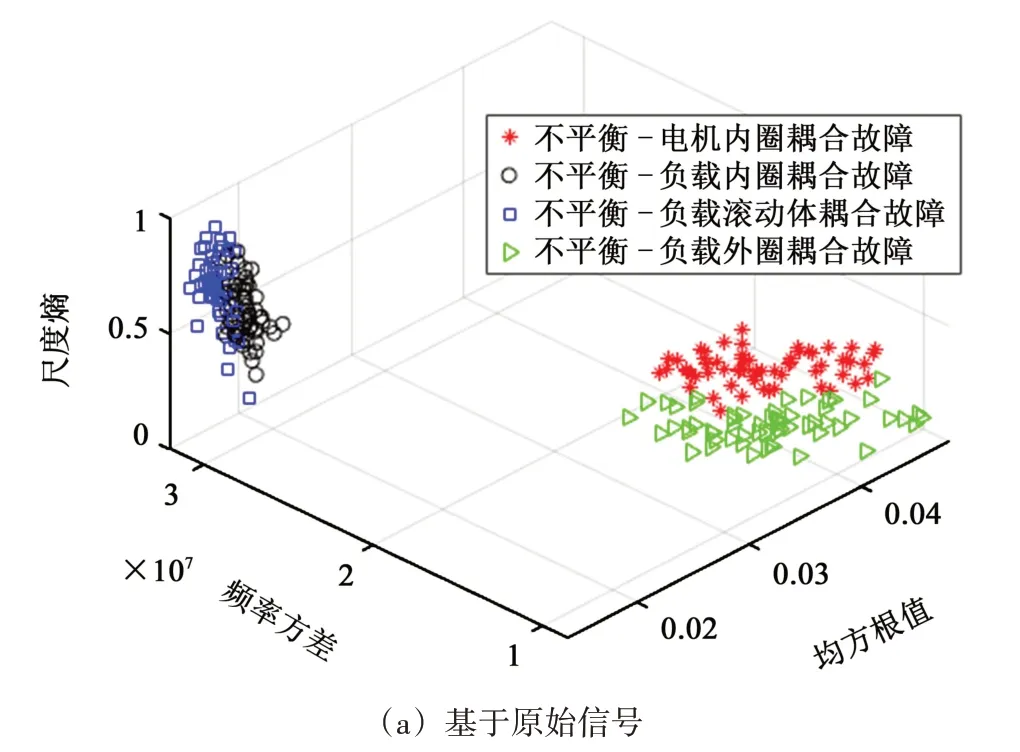
图10 耦合故障信号特征分布图Fig.10 Coupling fault feature distribution diagram

由图10 中可以看出，对比基于原始信号和基于优化稀疏重构后信号的三维特征空间分布情况，原始信号特征在空间分布下很杂乱，不具有聚集性；而经过优化后的稀疏重构信号的各类耦合故障特征在空间中呈现出较好的聚类效果。从图11 中可以看出，原始信号预测分类出现了较多错误样本，而优化重构后信号预测样本分类结果的准确率明显提高。

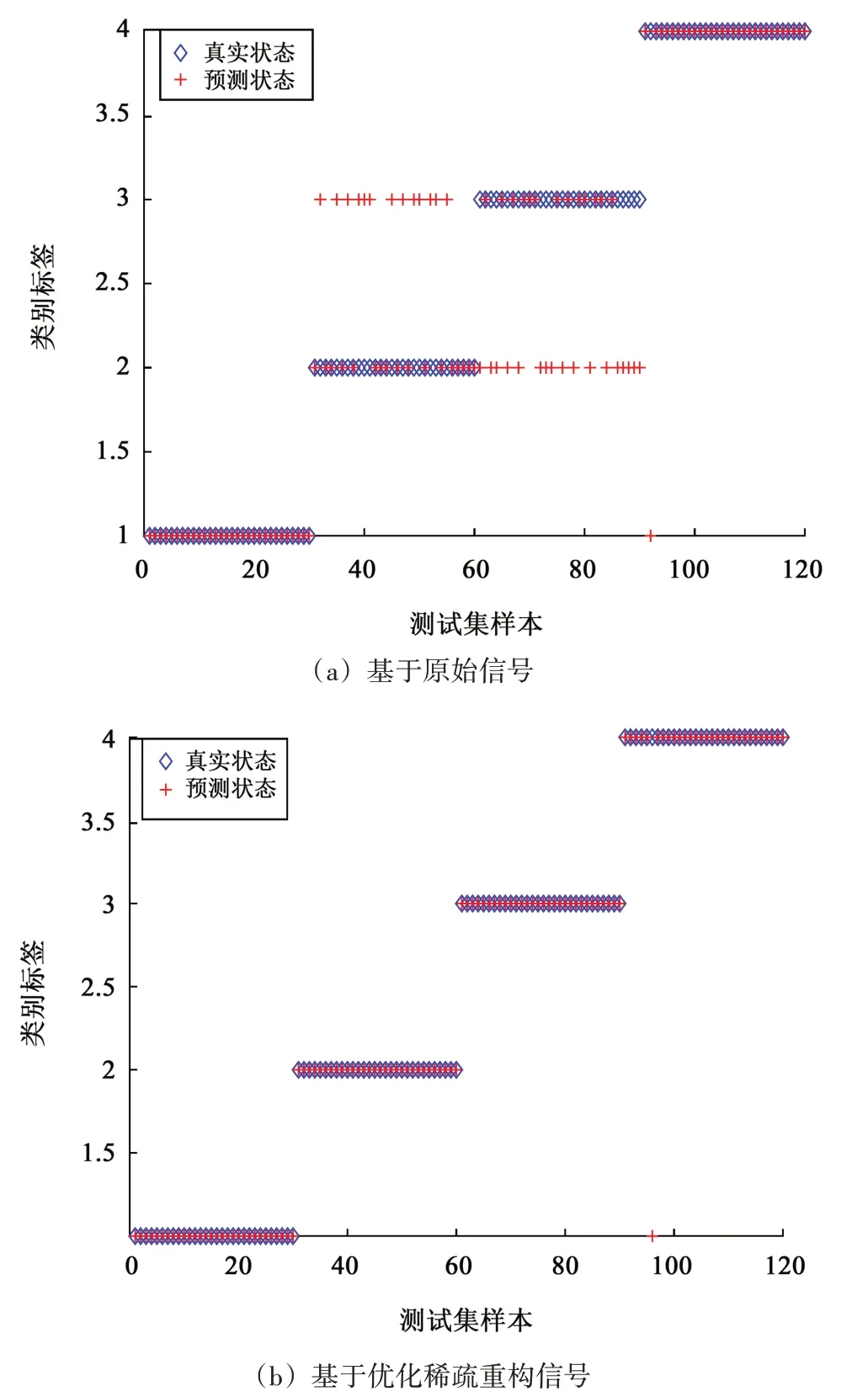
图11 耦合故障分类结果图Fig.11 Coupling fault classification diagram

为了进一步验证本文中所提方法的效果，又用后3 组案例按照案例1 的分析实验流程进行了验证。图12 所示为4 组案例的分类准确率结果。其中包含了基于原始信号和优化前后重构信号的分类效果。从图12 中可以看出，根据本文中方法优化参数后的稀疏重构信号在4组案例中的分类准确率较原始信号和优化前都有明显提升。其中，案例1中针对纯耦合故障信号的分类准确率较优化前提高了8.34%，说明面对复杂耦合信号，本文中方法具有优越性。

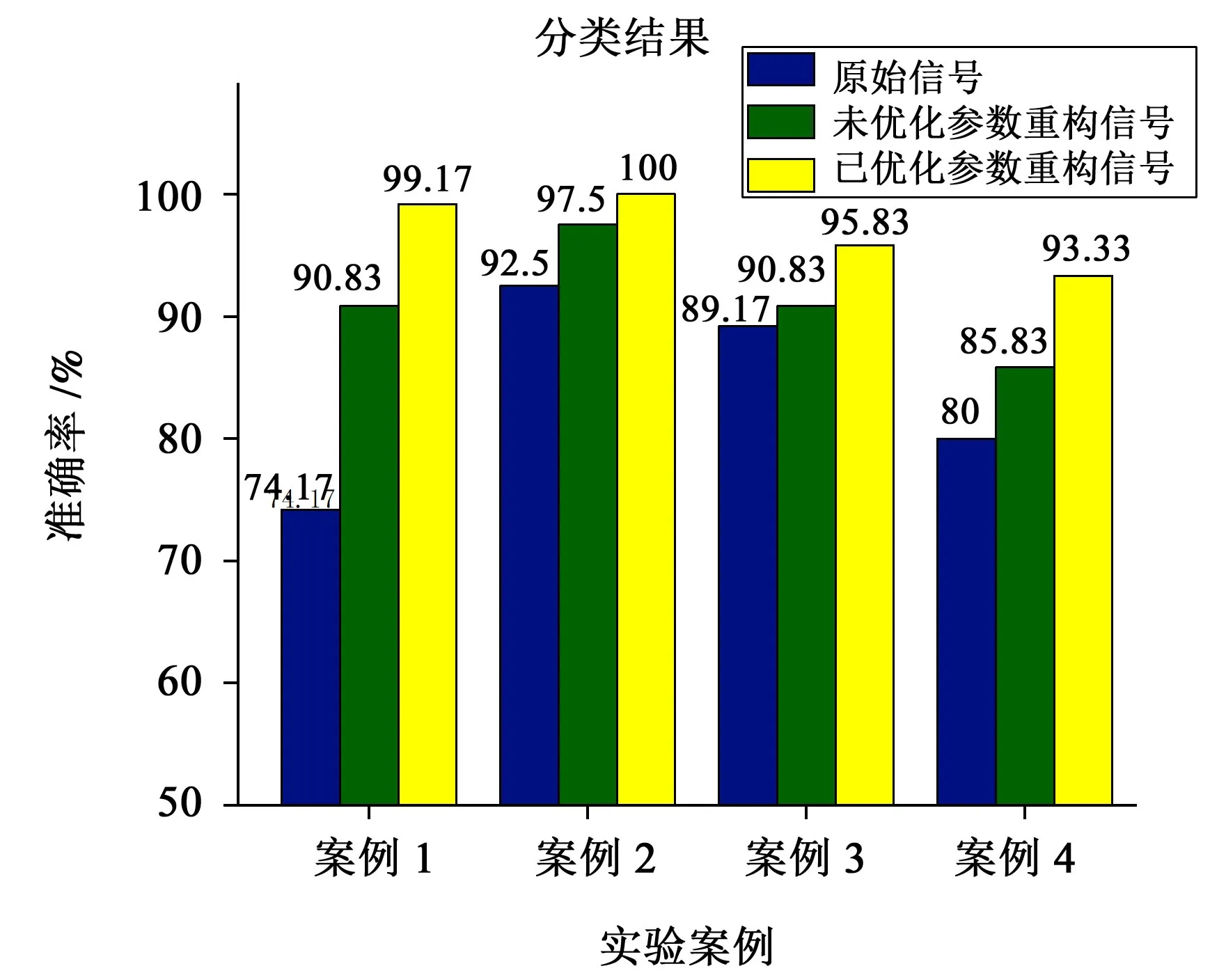
图12 4组案例的分类准确率Fig.12 Classification accuracy of four cases

4 结论

针对转子系统不平衡-轴承耦合故障信号中的弱故障特性，提出了多步网格搜索优化稀疏诊断方法。通过引入多步网格搜索算法优化Gabor原子的位移因子和频率因子两个参数，降低参数设置对重构误差的影响，并采用均方根值、频率方差和尺度熵3种特征，对信号进行了基于径向基函数的SVM 的分类与识别。该方法不仅解决了稀疏表示中经验选取参数值的问题，而且提升了抗干扰能力。数值仿真和实验分析表明，相较于未优化参数的稀疏表示方法，本文中方法具有明显的优势。具体结论如下：

（1）在低噪声干扰下，所提方法完整地继承了稀疏表示方法的优点，可有效提取信号的循环特征，突出信号的冲击成分，保证了参数优化后稀疏表示的准确性。

（2）当耦合故障特征的噪声干扰增大时，所提方法对轴承耦合故障信号的降噪效果明显，有效降低了噪声对耦合故障中弱故障特征的影响，提升了稀疏表示的降噪能力和抗干扰能力。

（3）所提方法实现了稀疏表示中的参数择优，提高了算法运行效率，使稀疏表示的重构时间更短，优化后的重构信号分类效果更好，准确率更高。