计及多状态啮合的面齿轮传动系统动力学建模与动态特性分析
2022-10-21朱凌云顾美华苟向锋
朱凌云 顾美华 苟向锋
(天津工业大学 机械工程学院, 天津 300387)
0 引言
面齿轮传动系统由主动直齿轮和共轭面齿轮组成,用于传递相交轴或交叉轴之间的运动和动力。因其具有结构紧凑、体积小、重合度大、传动功率大、分流效果好、噪声低等诸多优点,已被广泛应用于直升机、航空减速器等对空间占用和质量要求严格的重要传动装置中。
自20 世纪50 年代美国Fellows Gear Shaper 公司报道了面齿轮加工方法以来[1],越来越多的学者开始致力于面齿轮的研究。Litvin 等[2-5]在面齿轮的设计理论、加工方法、应力分析等方面做出了杰出贡献。Feng等[6]建立了渐开线斜齿面齿轮传动全齿面的精确模型。Zhou等[7]提出了一种生成面齿轮齿面几何形状的新型包络法,并用于面齿轮的数控铣削加工。Fu等[8]提出了一种新的面齿轮齿廓修形方法,可精确控制其修形参数。
随着齿轮设计方法及制造工艺的成熟,动态特性对齿轮传动过程中的稳定性和可靠性的影响逐渐成为研究的重点。Lin 等[9-10]建立曲面齿轮传动系统的非线性动力学模型,研究了不完全振动的运动响应及扭转振动。Li等[11]建立面齿轮传动系统的4 自由度动力学模型,研究了小齿轮齿根疲劳裂纹对面齿轮传动动力学行为的影响。Chen 等[12-14]建立6 自由度面齿轮副动力学模型,研究了修形及时变啮合刚度对系统动态行为的影响。Chen 等[15]利用有限元法计算面齿轮的时变啮合刚度,分析了传动误差激励对面齿轮传动系统非线性动力学特性的影响。冯光硕等[16]提出了面齿轮非对称时变啮合刚度的计算方法。林腾蛟等[17]研究了面齿轮传动系统的弯扭动力学模型中的分岔、准周期运动和混沌现象。
通常,面齿轮传动系统非线性动力学建模主要采用集中质量法,模型中考虑了诸如输入和输出轴激励、时变啮合刚度、齿侧间隙、传动误差和啮合阻尼等因素。已有研究结果对揭示面齿轮传动系统的非线性动力学特性非常有效,但无法获得系统的啮合条件和动态啮合力。Shi 等[18]提出了一种基于多状态啮合的直齿轮副动力学建模方法,分析其动态啮合力与啮合状态的变化,为研究齿轮传动中的振动提供了新思路。
本文中建立了接近面齿轮传动系统实际工作状态的非线性动力学模型,考虑各种啮合参数及实际啮合齿廓和由重合度所引起的多状态啮合,计算了系统动态啮合力的变化及载荷对其非线性动力学的影响。
1 非线性动力学模型
面齿轮传动系统由直齿圆柱齿轮和面齿轮组成。主动轮为输入轴上的直齿轮,其质量、转动惯量、驱动力矩和齿数分别为mp、Ip、Tp和Zp;从动轮为输出轴上的面齿轮,其质量、转动惯量、阻抗力矩和齿数分别为mf、If、Tf和Zf;Ifx为面齿轮在x轴上的转动惯量;y轴和z轴分别为直齿轮和面齿轮的轴线。如图1所示,面齿轮传动系统可简化为6自由度的含刚性支撑的弯扭摆振动系统。系统参数如表1所示。
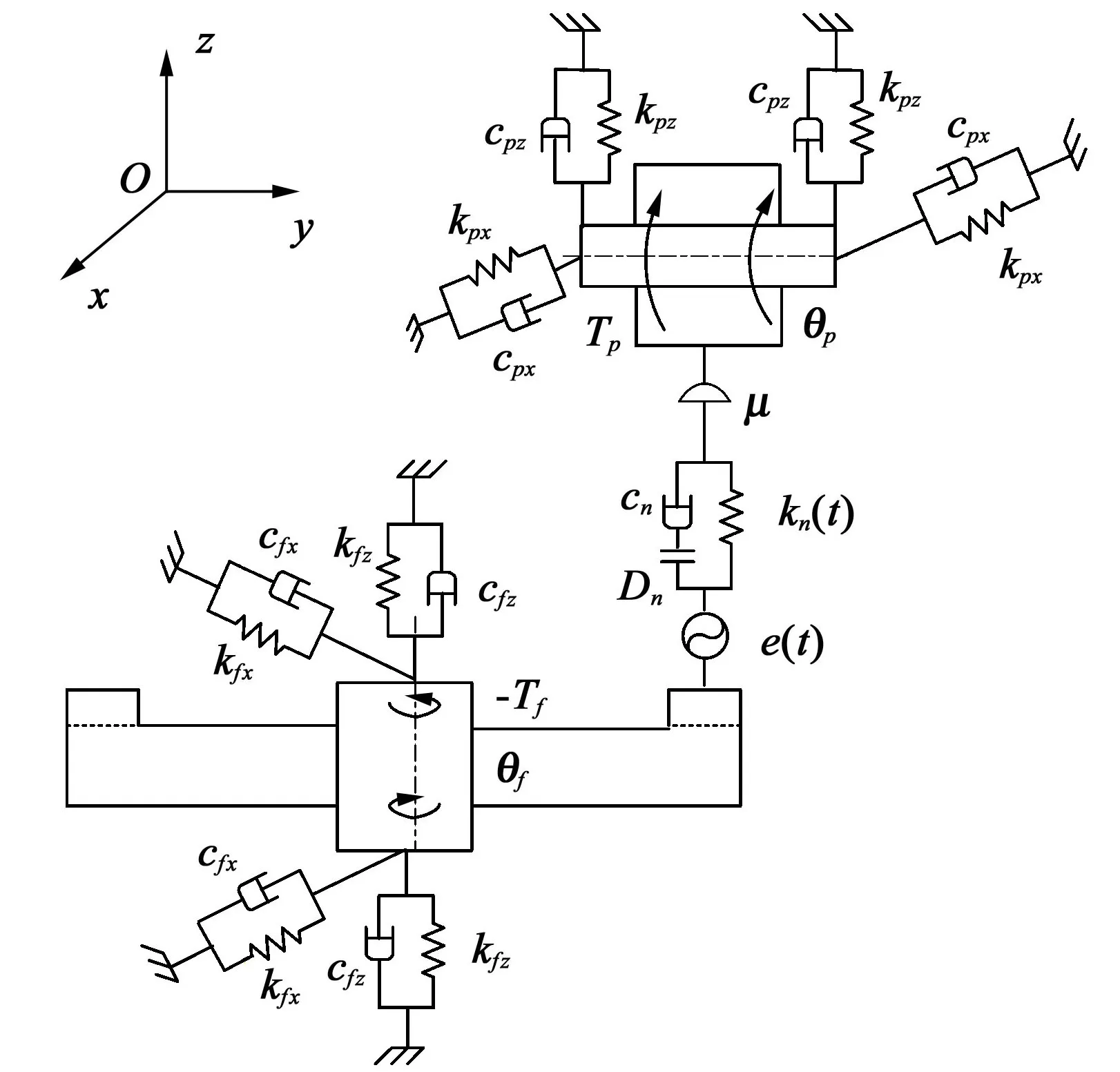
图1 面齿轮传动系统简化物理模型Fig.1 A simplified physical model of face-gear transmission system
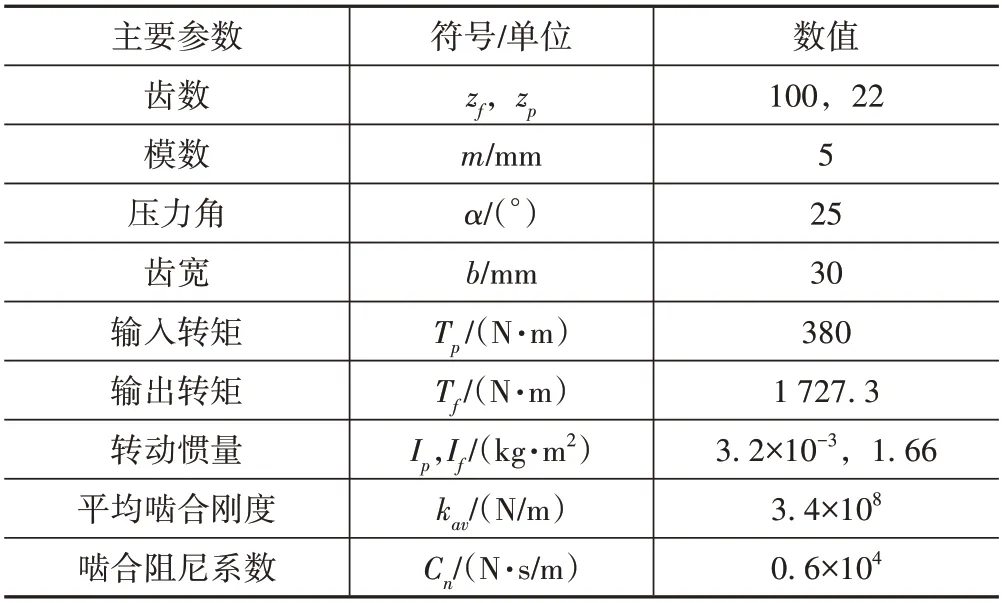
表1 面齿轮传动系统参数Tab.1 Parameters of the studied face-gear transmission system
面齿轮传动系统的重合度大于1.0,且存在齿侧间隙,传动过程中会出现齿面啮合、齿背接触和脱啮等3种啮合状态。分别建立了其非线性动力学模型。
1.1 考虑多状态啮合的弯扭摆模型
齿面啮合、齿背接触和脱啮状态下的受力分别如图2(a)、图2(b)、图2(c)所示。直齿轮沿z轴和x轴的平动位移分别为zp和xp;绕y轴的角位移为θp。面齿轮沿z轴和x轴的平动位移分别为zf和xf;绕z轴的旋转角位移为θf;绕x轴的扭摆角位移为θfx。齿面啮合时,直齿轮驱动面齿轮沿啮合线N1N2运动;齿背接触时,面齿轮推动直齿轮沿接触线M1M2运动。Fnp1、Fnp2分别为沿啮合线N1N2或接触线M1M2方向作用在直齿轮轮齿上的正压力;Fnf1、Fnf2分别为沿啮合线N1N2或接触线M1M2方向作用在面齿轮轮齿上的正压力;Fmp1、Fmp2、Fmf1和Fmf2分别为垂直于啮合线N1N2或接触线M1M2的摩擦力。
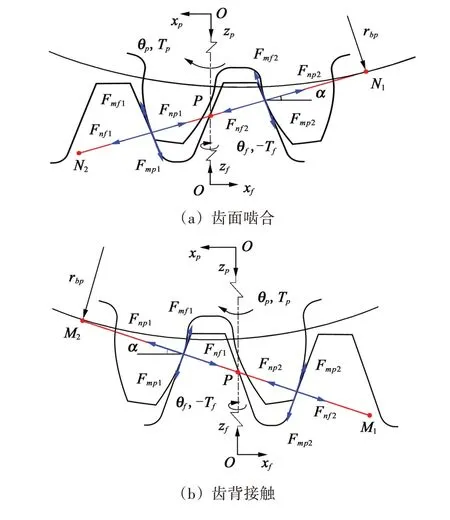
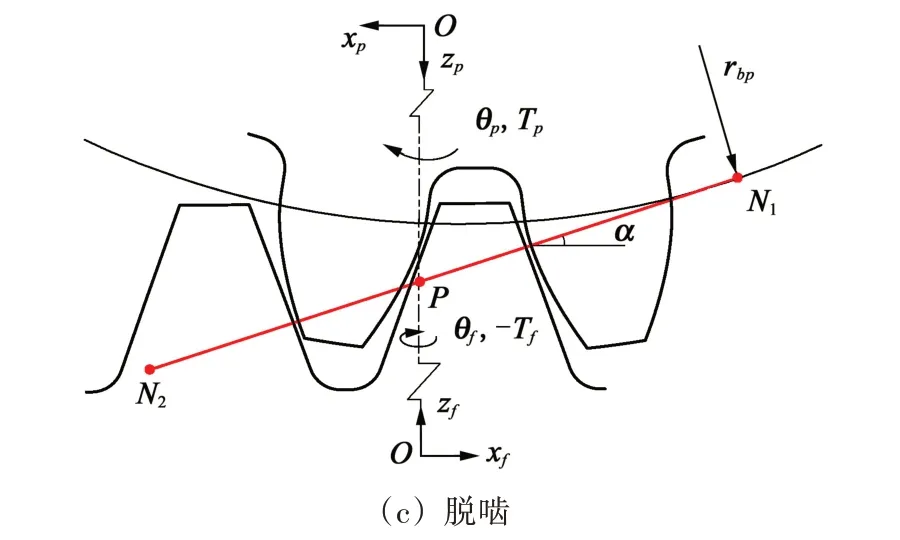
图2 面齿轮受力示意图Fig.2 Force diagram of a face-gear transmission system
根据齿轮啮合原理,啮合轮齿处于双齿区时,齿面啮合状态下,沿啮合线N1N2方向的总动态啮合力大于0,即Fnf1+Fnf2>0;沿啮合线N1N2方向的相对位移大于齿侧间隙的一半,即x0>Dn。齿背接触状态下,沿接触线M1M2方向的总动态啮合力小于0,即Fnf1+Fnf2<0;沿接触线M1M2方向的相对位移小于齿侧间隙一半的负值,即x0<-Dn。脱啮状态下,作用在轮齿上的力为0,相对位移满足-Dn<x0<Dn。啮合轮齿处于单齿区时,上述条件中,Fnp1、Fnf1均为0。多状态下的系统绝对扭弯摆振动方程为
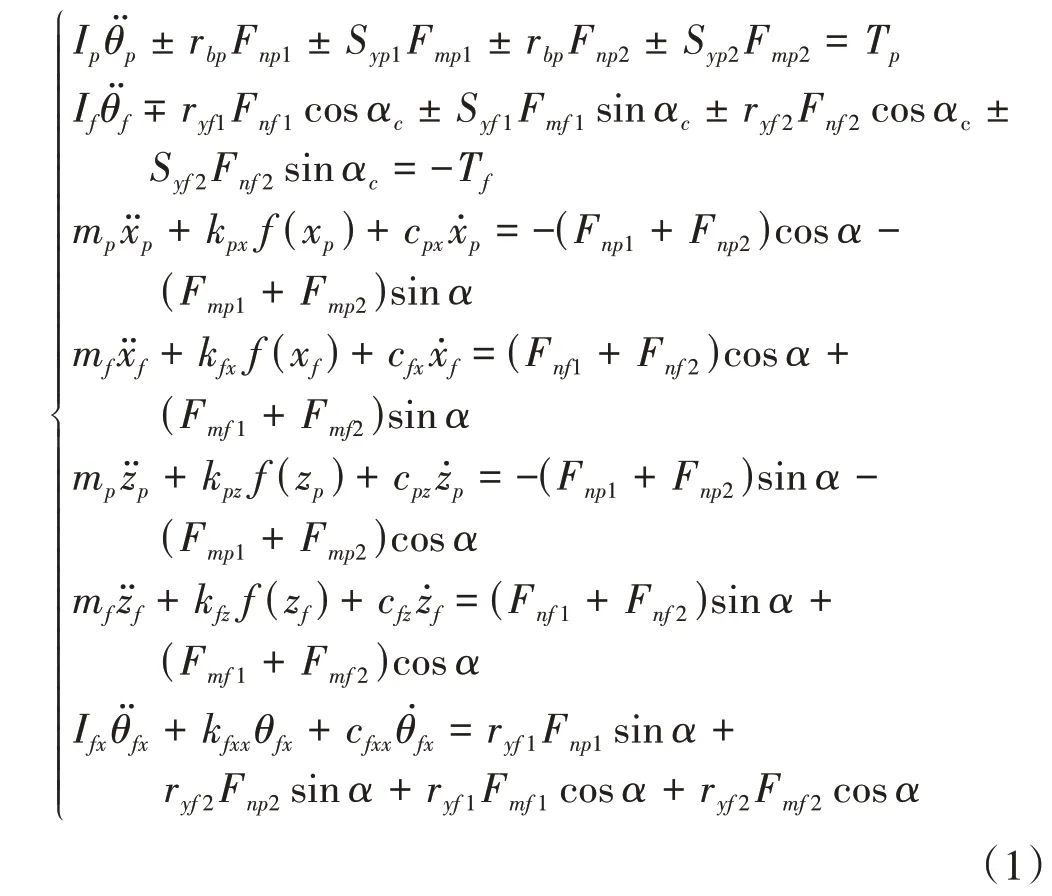
式中,cpx和cpz分别为输入轴上轴承沿x轴和z轴的支承阻尼系数;kpx和kpz分别为输入轴上轴承沿x轴和z轴的支承刚度;cfx和cfz分别为输出轴上轴承沿x轴和z轴的支承阻尼系数;kfx和kfz分别为输出轴上轴承沿x轴和z轴的支承刚度;cfxx和kfxx分别为面齿轮在x轴上的扭转阻尼系数和支撑刚度;f(xp)和f(zp)分别为轴承在输入轴上的间隙函数;f(xf)和f(zf)分别为轴承在输出轴上的间隙函数;在“±”和“∓”中,当齿面啮合时,分别取两符号上部的“+”和“-”;当齿背接触时,分别取两符号下部的“-”和“+”。
沿N1N2或M1M2方向作用在直齿轮和面齿轮第i对齿上的正压力为

式中,Lyi(τ)(y=u,v;i=1,2)为第i对轮齿的载荷分配系数,u和v分别对应齿面啮合和齿背接触状态。
沿啮合线方向的总动态啮合力为
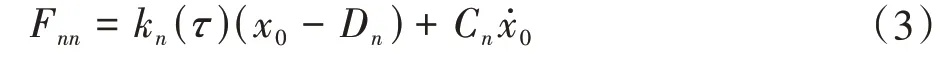
式中,τ为时间;kn(τ)、Cn分别为时变啮合刚度和啮合阻尼系数;x0为沿啮合线方向的相对位移,x0=rbpθp+xpcosα+zpsinα-ryf2θf-xfcosα-zfsinα-e(τ);e(τ)为综合传递误差;Dn为齿侧间隙的一半。
面齿轮传动中,直齿轮不受轴向力,面齿轮不受径向力。根据其啮合原理及点接触原理,面齿轮副所受法向力始终与直齿轮的基圆相切,则啮合线是一条与直齿轮基圆相切的直线。可见,啮合点到直齿轮回转中心和面齿轮回转中心的距离都是时变的,且摩擦力的方向总是与啮合线垂直。
垂直于N1N2和M1M2的摩擦力为
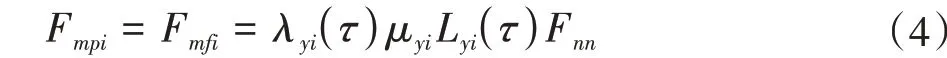
式中,μyi为齿面摩擦因数。
摩擦力方向系数为

式中,rp为直齿轮节圆半径;rypi(τ)、ryfi(τ)分别为第i对轮齿上啮合点到直齿轮和面齿轮中心的距离,计算式分别如式(6)、式(7)所示。
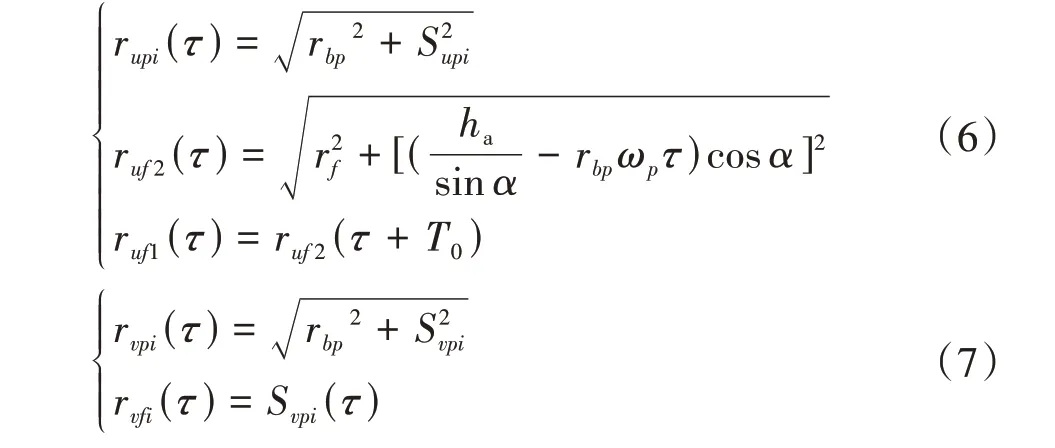
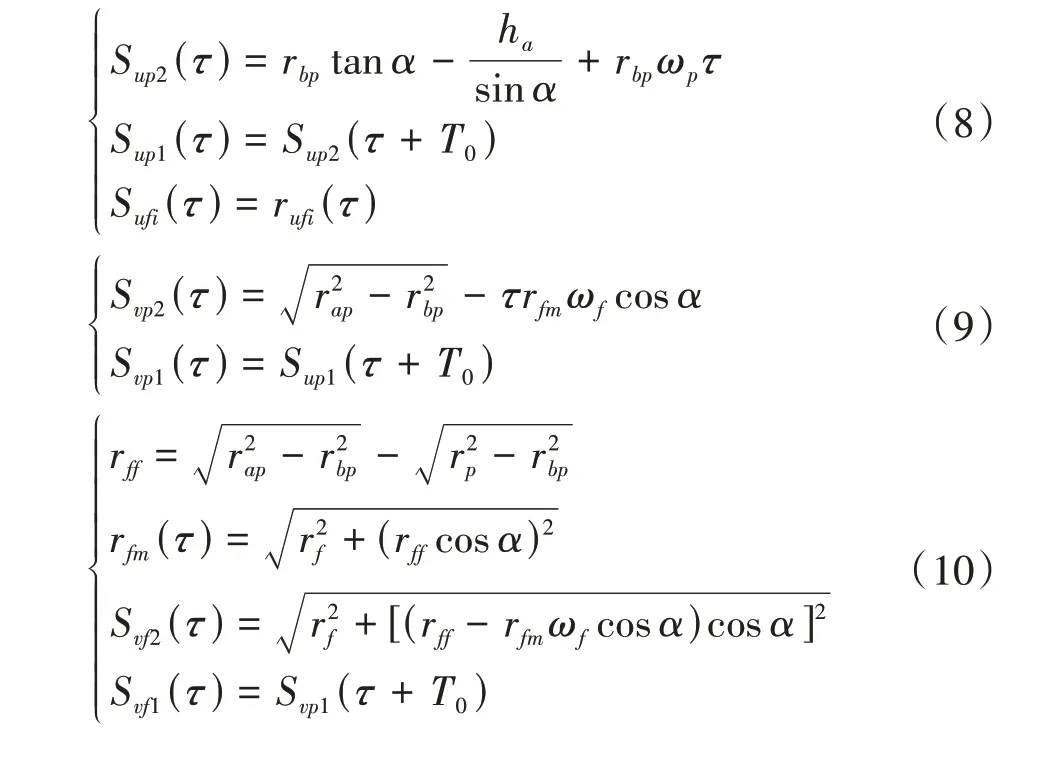
式中,Sypi、Syfi分别为第i对轮齿上啮合点到直齿轮和面齿轮中心的摩擦力臂,计算式分别由式(8)~式(10)所示。式中,ha为齿顶高;α、ωp分别为直齿轮节圆压力角和角速度;αc为面齿轮压力角,αc=α+arccos(rf/ryfi);rf为节点到面齿轮轴心的距离,rf=mzf/2;T0为单双齿交替啮合周期,T0= 2π/zpωp;rff、rfm分别为点M1到点P和回转中心的距离。
将式(1)无量纲化,即为
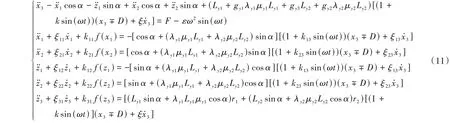

式中,q分别代表x1、x2、z1和z2;d为轴承间隙,d=bpx/D0=bpz/D0=bfx/D0=bfz/D0。
1.2 系统无量纲归一化弯-扭-摆模型
齿侧间隙和重合度大于1.0,决定面齿轮传动系统存在单/双齿齿面啮合、单/双齿齿背接触和脱啮等多种啮合状态。相对位移大于齿侧间隙的一半且啮合力大于0,即x3≥D且Fn>0时,系统处于单/双齿齿面啮合;x3≤D且Fn<0 时,系统处于单/双齿齿背接触;当-D<x3<D且Fn= 0时,系统发生脱啮。
定义啮合力在x方向的状态函数rx(t,x3)为
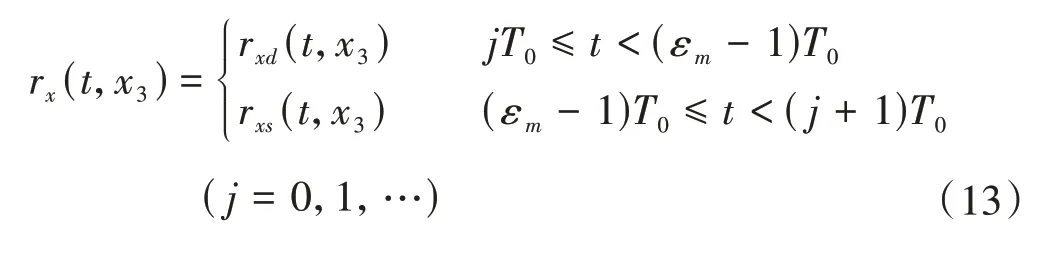
式中,rxd(t,x3)、rxs(t,x3)分别为双、单齿啮合在x方向的状态函数,可分别由式(14)和式(15)求得;j为周期数。
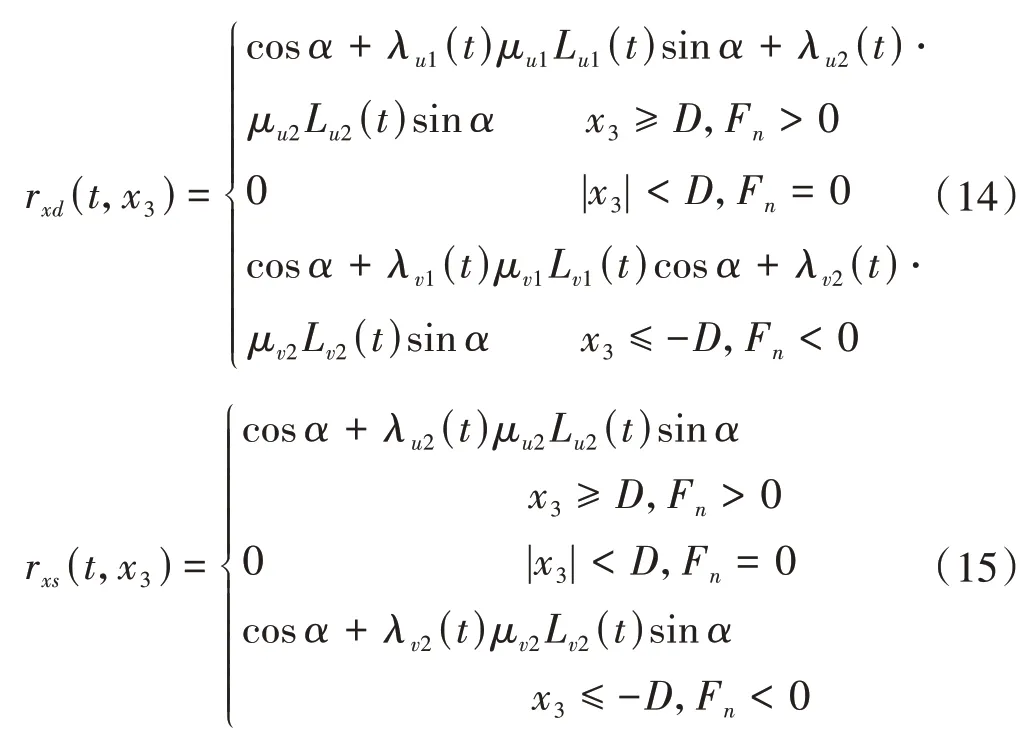
定义啮合力在z方向的状态函数rz(t,x3)为
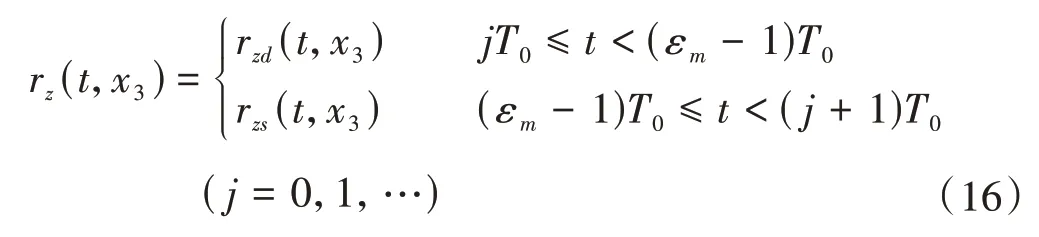
双齿啮合和单齿啮合在z方向的状态函数rzd(t,x3)和rzs(t,x3)可分别由式(17)、式(18)求得。
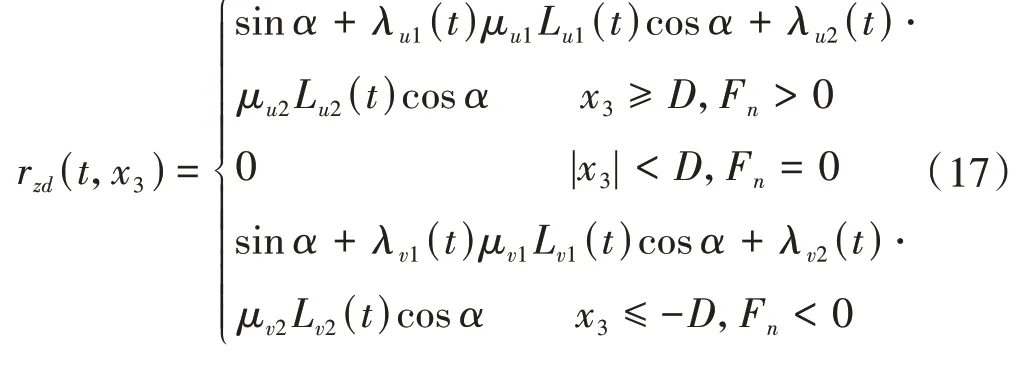
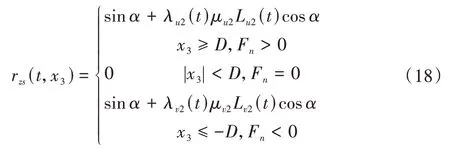
啮合状态函数h(t、x3)、rzf(t、x3)可分别由式(19)、式(20)求得。

式中,hd(t,x3)、rzfd(t,x3)和hs(t,x3)、rzfs(t,x3)分别为双齿啮合和单齿啮合的状态函数,可分别由式(21)~式(24)求得。
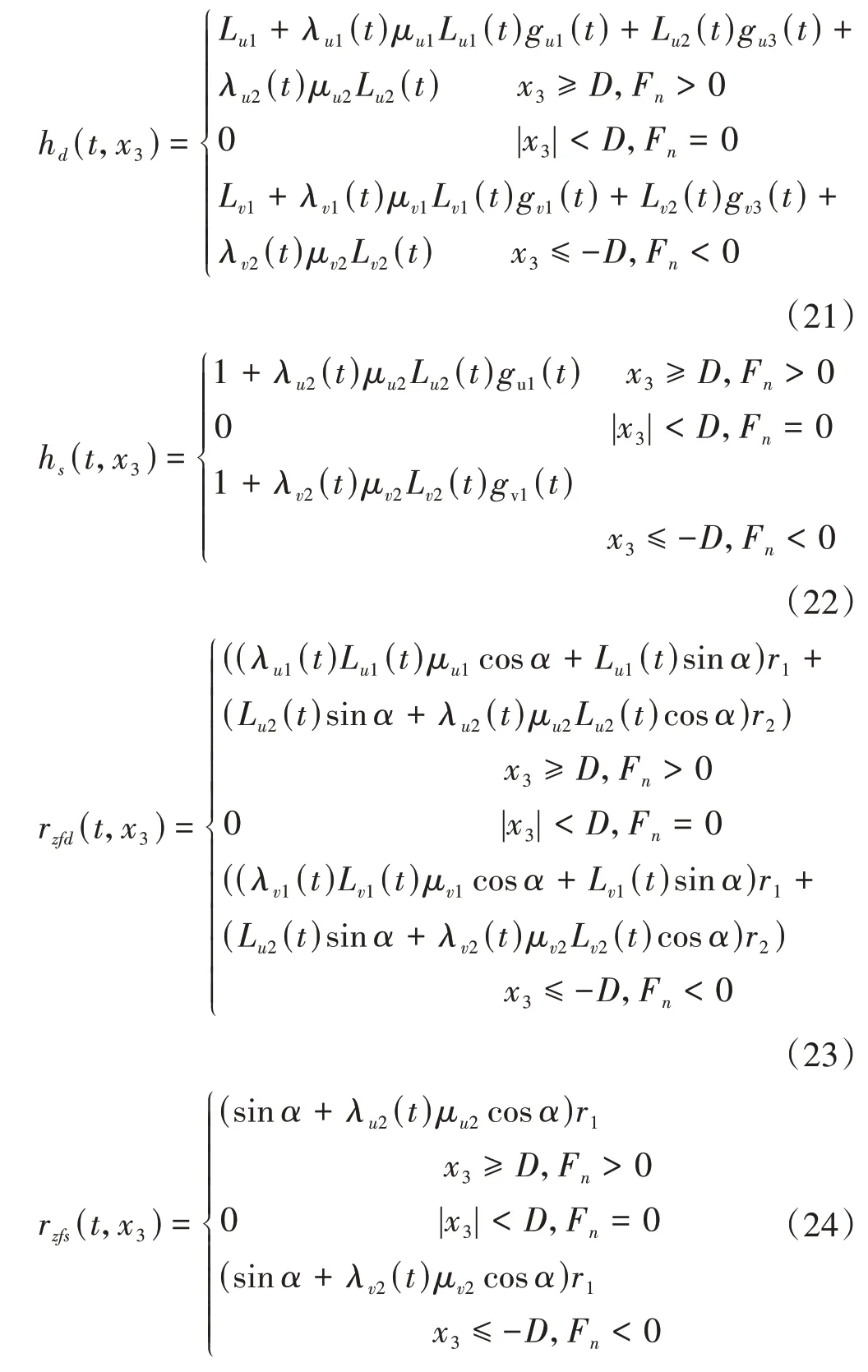
将状态函数式(15)~式(26)引入到面齿轮传动系统非线性动力学模型中,则可化为包含5种状态的无量纲归一化扭弯摆模型,即
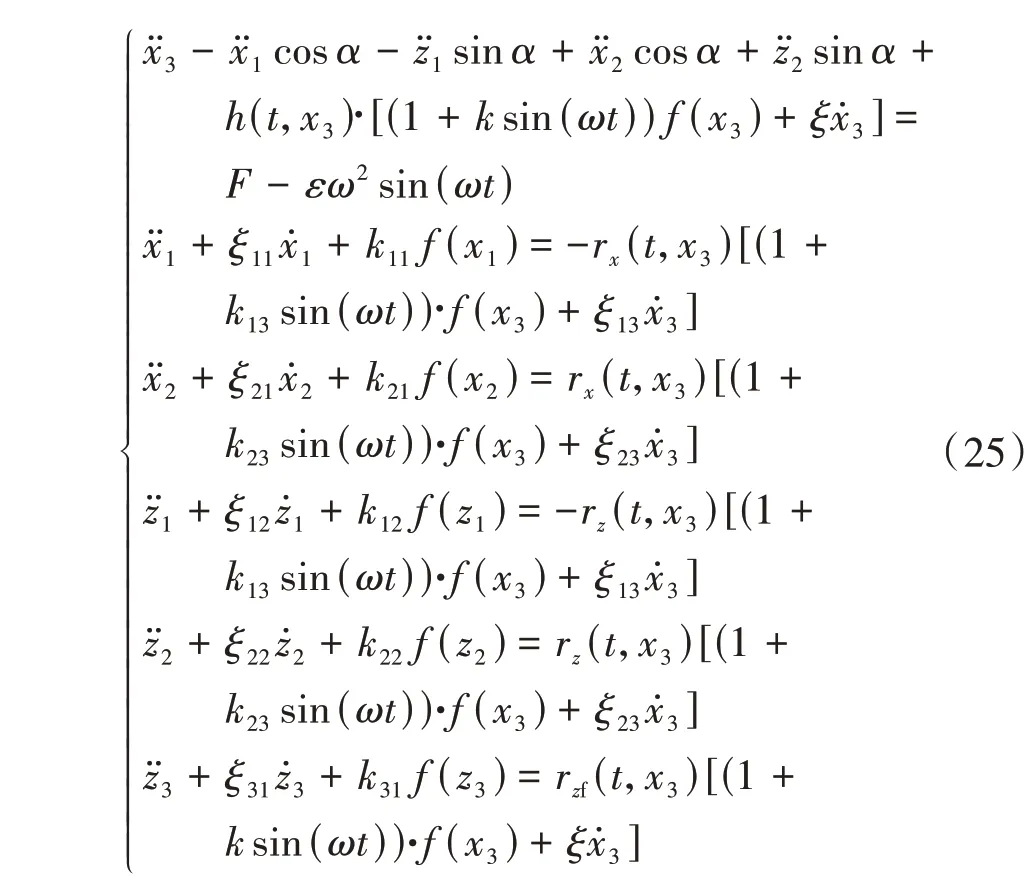
式中,f(x3)为齿侧间隙函数,计算式为
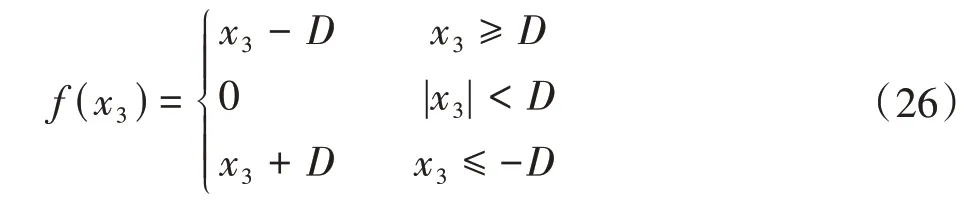
无量纲非线性动态啮合力Fn可用来判别啮合状态,其方向与x3相同,可由式(27)计算得到。
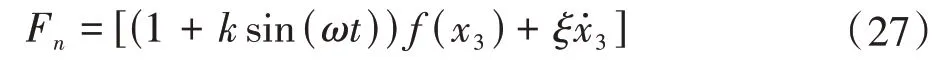
由式(27)中可见,与现有非线性动力学模型相比,本文中所建立的含多状态啮合的系统扭弯摆非线性模型中,考虑了啮合刚度、载荷分配率、摩擦、齿侧间隙和综合传动误差等因素,有以下特点:①包含的状态函数h(t,x3)和rzf(t,x3)可以准确反映面齿轮传动系统的啮合状态。②包含的状态函数rz(t,x3)明确区分了单齿啮合和双齿啮合。③可通过方程中有关齿廓的时变参数来分析齿廓变形和修形对面齿轮系统的影响。④动态啮合力可准确说明其对啮合状态的影响。
2 动态啮合力与啮合状态分析
根据重合度计算方法,可得面齿轮的近似重合度εm=1.72。此时,啮合齿对出现单、双齿交替,其啮合区域划分如图3 所示。图3 中,AD为啮合线的工作部分,A和D分别为啮入点和啮出点,P为节点,BC为单齿啮合区(对应轮齿上的B1C1),AB和CD为双齿啮合区(对应轮齿上的A1B1和C1D1)。沿啮合线AD的载荷分配率可根据文献[19]求得。
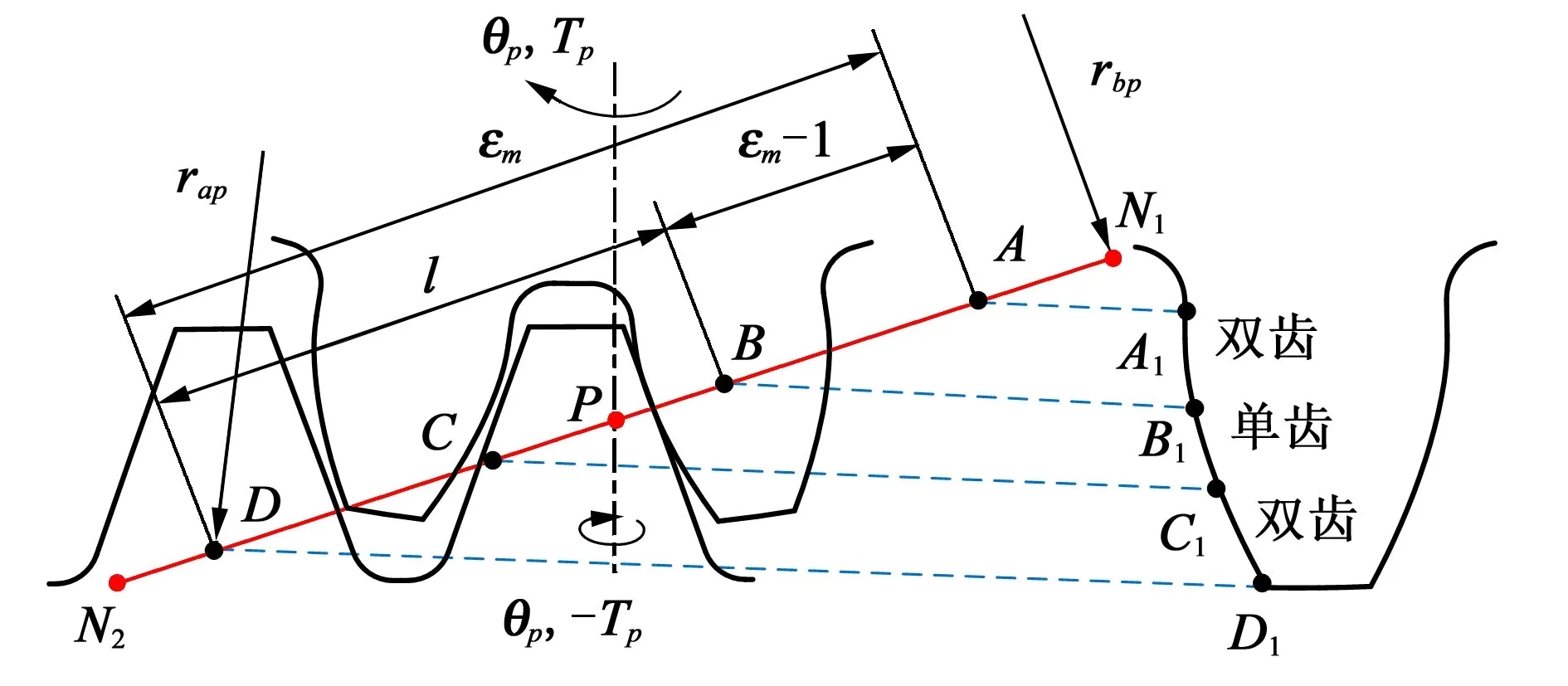
图3 沿啮合线啮合区域的划分Fig.3 Division of engagement area along the action line
为了说明动态啮合力与啮合状态之间的关系,啮合频率ω分别取1.1、2.1和3.4,分析其动态特性及不同啮合状态发生机理。式(25)中的其他无量纲参数取k11=k12=k13= 0.15,k21=k22=k23= 0.3,k31= 0.3,k32=0.32,k33= 0.31,k= 0.3,ξ31= 0.06,ξ32= 0.07,ξ33= 0.012,ξ11=ξ12= 0.01,ξ23= 0.07,ξ= 0.05,ξ13=ξ21=ξ22= 0.06,ε= 0.2,F= 0.14。
2.1 齿面啮合
图4所示为啮合频率ω=1.1时,面齿轮传动系统动态啮合力随无量纲时间t的变化及其相图。由图4中可见,动态啮合力始终大于0,相对位移x3大于无量纲齿侧间隙D的一半,表明系统处于齿面啮合状态,未发生脱啮、齿背啮合。图5所示为ω=1.1时的载荷分配率(图5(a))和动态啮合力(图5(b))沿啮合线的分布图。图5 中,点A和点D分别为啮入点和啮出点。根据载荷分配率,动态啮合力不均匀地分配给两对齿。当啮合点从点A移动到点B时,n+1 齿对上的动态啮合力逐渐减小,n齿对上的动态啮合力增加。n+1齿对在点B处分离,系统进入单齿啮合;n-1 齿对在点C进入啮合。单双齿切换时,动态啮合力发生突变。动态啮合力的波动增加了系统的不稳定性,会导致齿轮在运行时产生振动。
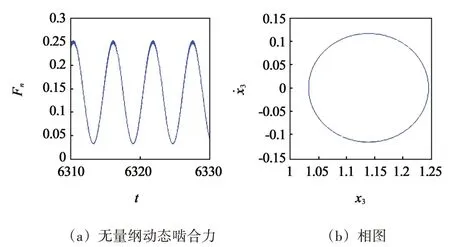
图4 系统动态特性(ω=1.1)Fig.4 Dynamic characteristics of the system(ω=1.1)
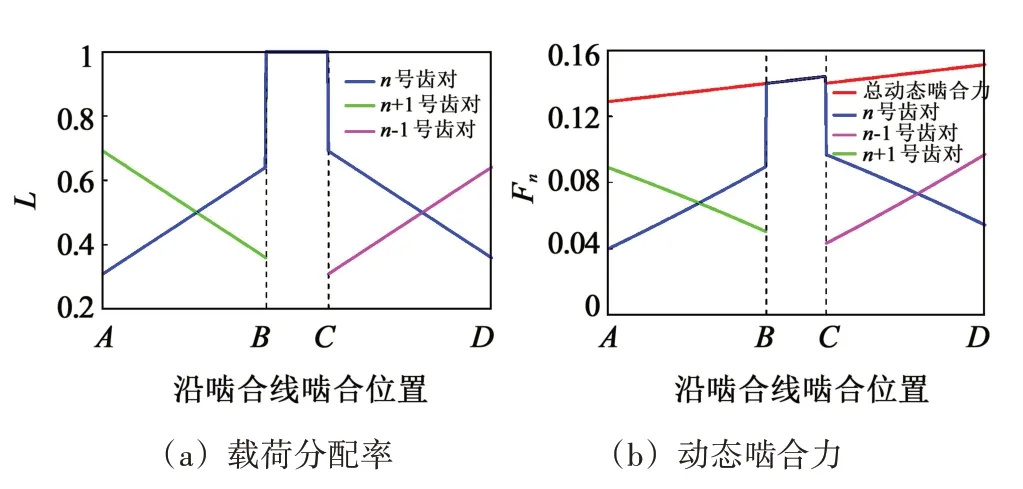
图5 ω=1.1时沿啮合线的动态特性Fig.5 Dynamic characteristics along the action line when ω=1.1
2.2 脱啮
图6所示为啮合频率ω=2.1时,系统的动态啮合力随无量纲时间t的变化及其相图。由图6 中可见,动态啮合力周期性地出现等于0的情况,其相对位移x3也会小于无量纲齿侧间隙D的一半。这表明脱啮周期性发生。齿面啮合与脱啮交替进行将使齿轮传动系统运行不平稳。图6(a)中的局部放大图揭示了从齿面啮合切换到脱啮时,动态啮合力发生突变,加剧了系统振动。
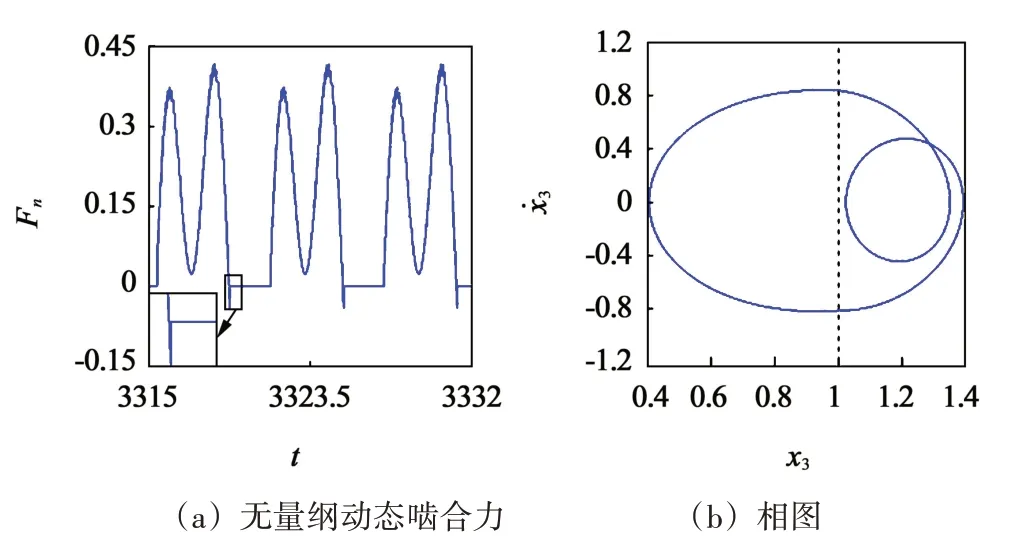
图6 系统动态特性(ω=2.1)Fig.6 Dynamic characteristics of the system(ω=2.1)
图7 所示为ω=2.1 时,载荷分配率(图7(a))和动态啮合力(图7(b))沿啮合线的分布图。当啮合点在单齿啮合区内从点C移动到点D时,n齿对和n-1齿对上的总动态啮合力及其分量逐渐减小。总动态啮合力在点a处减小至0,预示啮合齿对即将发生脱啮。随着动态啮合力的反向增加,最终发生齿面脱离。动态啮合力的波动会导致啮合状态发生变化。总动态啮合力的波动将引起面齿轮传动系统中出现轮齿脱离、产生振动。
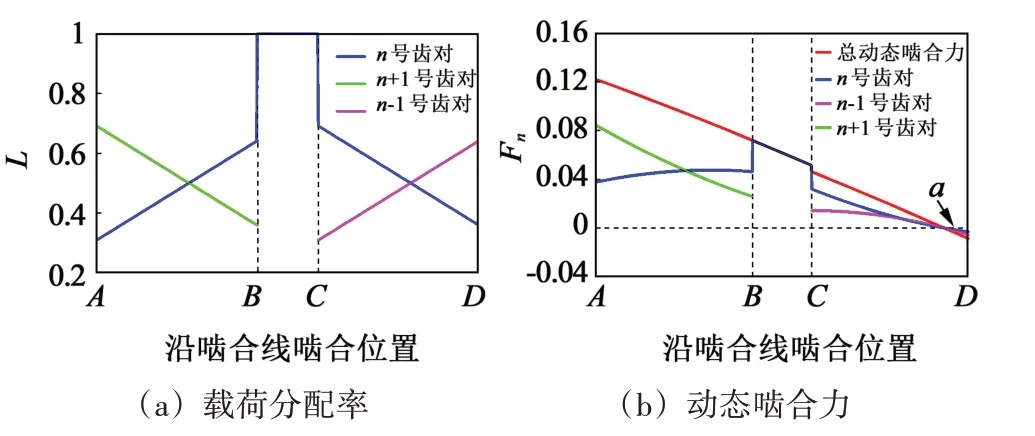
图7 ω=2.1时沿啮合线的动态特性Fig.7 Dynamic characteristics along the action line when ω=2.1
2.3 齿背接触
图8所示为啮合频率ω=3.4时,系统出现齿背接触,其动态啮合力随无量纲时间t的变化及其相图。动态啮合力的大小出现了Fn>0、Fn=0 和Fn<0 三种情况,相对位移x3也对应地出现了x3>D、D<x3<-D和x3<-D三种情况,这说明此时系统中出现了齿面啮合、脱啮和齿背接触三种情况。由图8(a)中的局部放大部分可以看出,啮合状态改变时,动态啮合力发生波动,导致了齿轮传动过程中的振动。
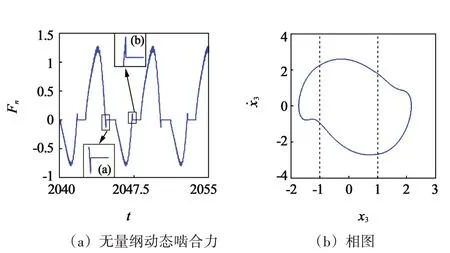
图8 系统动态特性(ω=3.4)Fig.8 Dynamic characteristics of the system(ω=3.4)
图9(a)、图9(b)和图9(c)、图9(d)所示分别为图8(a)中两处局部放大部分中从齿面啮合到脱啮的载荷分配率(图9(a))和动态啮合力(图9(b))和从齿背接触到脱啮时的载荷分配率(图9(c))和动态啮合力(图9(d))沿啮合位置的分布图。由图9(b)中可见,当啮合点从啮合线上的点A移动到双齿啮合区的点B时,动态啮合力减小,在点a处减小至0 后反向增加,其作用方向在点a处发生突变,说明啮合齿对即将脱啮。动态啮合力在单齿啮合区BC的点b处等于0,此时,面齿轮系统发生脱啮。动态啮合力的波动导致轮齿脱离。由图9(d)中可见,当啮合点从啮合线中的点A移动到啮合点C附近时,动态啮合力的绝对值减小。它在点a处减小至0 后增加。动态啮合力的作用方向在点a处突变,说明齿背接触状态即将结束。动态啮合力在双齿啮合区CD的点b处等于0,系统发生脱啮。动态啮合力的波动导致脱啮和振动。
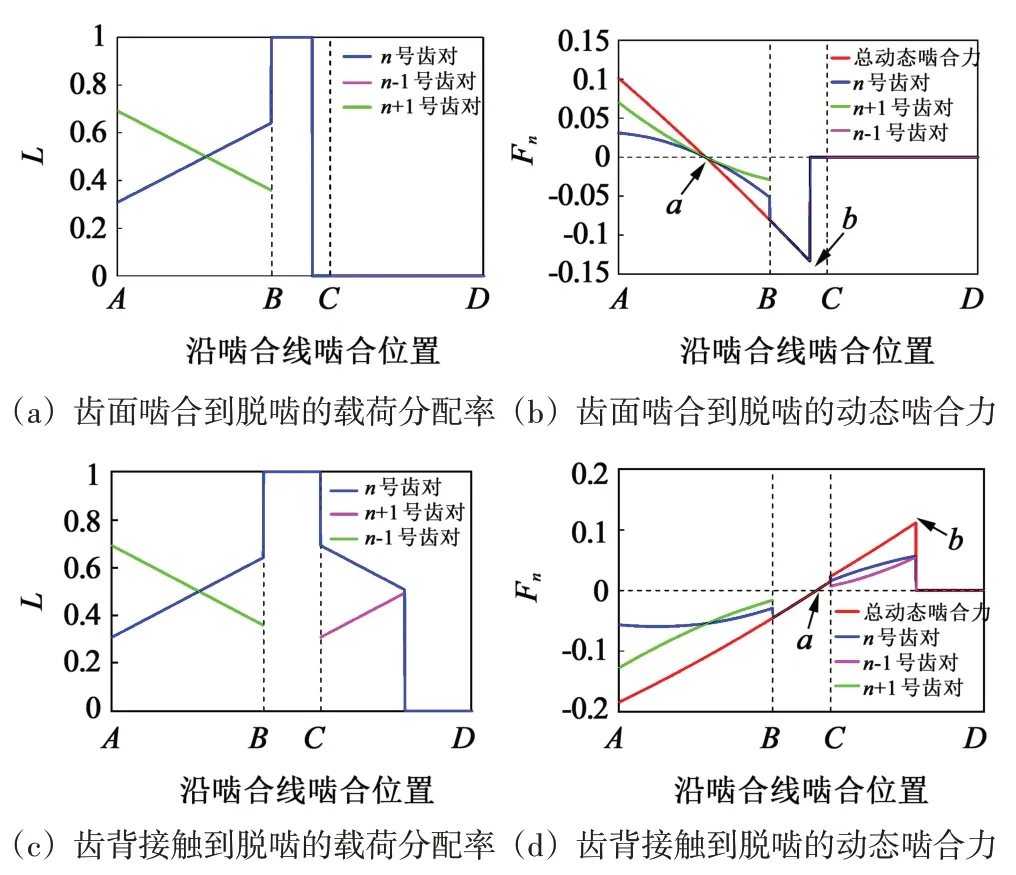
图9 ω=3.4时沿啮合线的动态特性Fig.9 Dynamic characteristics along the action line when ω=3.4
综上,由单对齿啮合和双对齿啮合交替产生的振动发生在啮合线的特定位置。由啮合状态的切换引起的齿面振动和齿背振动发生在啮合线的任何位置。动态啮合力在方向上的突变导致系统啮合状态的转变。
3 载荷对非线性动力学行为的影响
考虑多状态啮合的扭弯摆面齿轮传动系统具有强非光滑非线性特征,其解析求解困难。本文中采用4阶Runge-Kutta法数值求解,利用相图、Poincaré映射图、分岔图和最大Lyapunov 指数(TLE)图分析面齿轮传动系统的动力学行为。为了系统研究面齿轮传动系统的非线性动力学和多状态啮合特性,定义3个不同的Poincaré截面为:
(1)时间截面Poincaré 映射,Γn={(x1,ẋ1,x2,ẋ2,x3,ẋ3,z1,ż1,z2,ż2,z3,ż3,t) ∈R12×R+,mod(t,2π/ω) = 0}。
(2)齿面截面Poincaré 映射,Γp={(x1,ẋ1,x2,ẋ2,x3,ẋ3,z1,ż1,z2,ż2,z3,ż3,t) ∈R12×R+,x3=D}。
(3)齿背截面Poincaré 映射,Γb={(x1,ẋ1,x2,ẋ2,x3,ẋ3,z1,ż1,z2,ż2,z3,ż3,t) ∈R12×R+,x3= -D}。
数值求解不同截面的Poincaré映射。时间映射用于研究周期激励系统的周期解。相轨迹每次到达齿面截面/齿背截面时发生一次碰撞。基于齿面/齿背截面内的Poincaré 映射可以判断相轨迹和齿面/齿背间的接触次数。系统的周期性运动和碰撞特性由符号n-p-b来表征。其中,n为周期运动数;p、b分别为齿面碰撞和齿背碰撞的数量。
当齿轮系统在不同啮合状态之间切换时发生振动,对系统稳定性和可靠性造成影响。本小节中主要分析载荷对系统非线动力学的影响。
取无量纲参数k= 0.3,k11=k12=k13= 0.15,k21=k22=k23= 0.3,k31= 0.3,k32=0.32,k33= 0.31,ξ31=0.06,ξ32= 0.07,ξ33= 0.012,ξ11=ξ12= 0.01,ξ23=0.07,ξ= 0.05,ξ13=ξ21=ξ22=0.06,ε= 0.2,ω=2.6。系统随载荷增大的分岔图及对应的TLE 如图10 所示。其中,青色表示时间截面Γn内的分岔图,红色表示齿面截面Γp内的分岔图,蓝色表示齿背截面Γb内的分岔图。即青色为面齿轮传动系统随载荷变化时系统的动力学特性变化过程,可将其分解至齿面截面Γp(红色)及齿背截面Γb(蓝色)内。
由图10 中可见,当F<F1=0.005 1 时,系统按照1-1-0 的规律运动,在系统1 个周期1 运动内,因为发生了脱啮而出现1 次齿面碰撞,未发生齿背接触。图11中,“·”为时间截面映射点,“△”为齿面截面映射点。图11(a)、图11(b)所示分别为F=0.002 时的相图与动态啮合力。当载荷增大至F=0.005 1 时,系统进入混沌运动,其TLE 大于0,出现脱啮和齿背接触。图11(c)、图11(d)所示分别为F=0.01时的Poincaré 映射图和动态啮合力变化图。此时,啮合力在Fn>0、Fn=0 和Fn<0 间 变 化。当 载 荷 增 大 至F2=0.103 1 时,发生鞍结分岔,系统运动退化为2-1-0运动,在系统1 个周期2 运动内发生1 次齿面碰撞。图11(e)、图11(f)所示分别为F=0.105 时的相图、映射图与动态啮合力随时间的变化图。当载荷增大至F3=0.109 6 时,系统发生擦切,其齿面碰撞增至系统1 个周期2 运动内出现两次,系统运动为2-2-0,其相图、映射图与动态啮合力随时间变化如图11(g)、图11(h)所示。对照图11(f)、图11(h)可见,当F从左向右经过F3点之后,M区域中的动态啮合力从Fn>0 向Fn=0 的偏移,表明系统的部分相轨迹扩大并向齿面截面左侧移动,如图11(e)、图11(g)所示,齿面碰撞次数增加了一次。当载荷增大至F4=0.116 6时,系统发生逆倍化分岔,其TLE等于0,系统运动转迁为1-1-0。当F=0.177 1时,系统发生擦切,其相图、映射图与动态啮合力如图11(i)、图11(j)所示。当F>F5=0.177 1时,系统运动为1-0-0,不发生脱啮、齿面碰撞和齿背碰撞,其相对位移大于齿侧间隙的一半,动态啮合力始终大于0,如图11(k)和图11(l)所示。
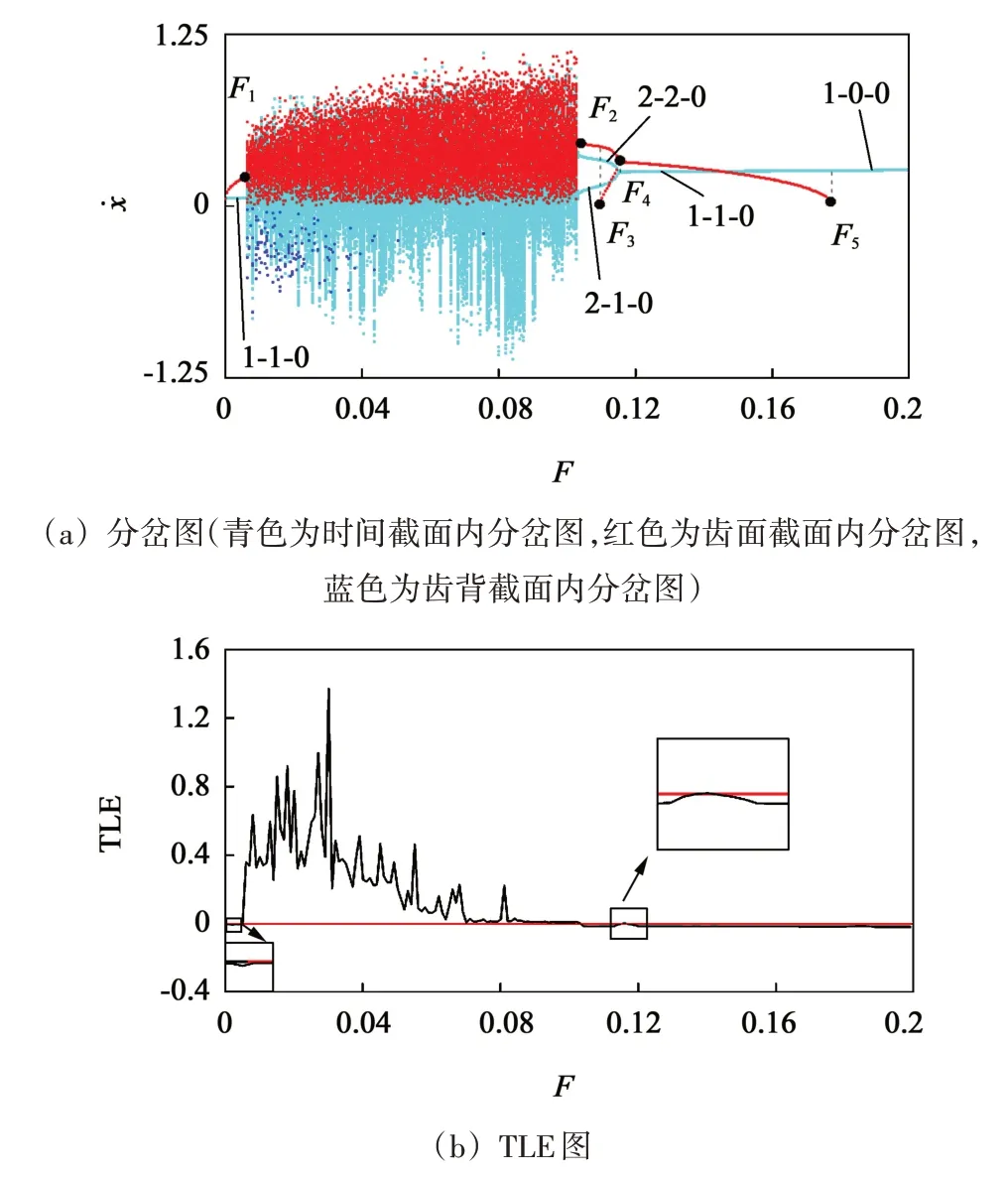
图10 系统随载荷F增大时的分岔图及TLE图Fig.10 Bifurcation diagram and TLE spectrum with the increase in load F
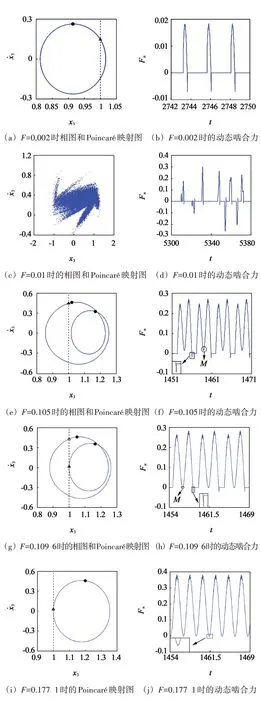

图11 系统的相图、Poincaré映射图及动态啮合力Fig.11 Phase diagram,Poincaré mappings and the dynamic engaging force of the system
可见,当载荷较大时,面齿轮传动系统的非线性动力学和振动特性相对稳定。当载荷系数较小时,系统出现分岔和混沌运动,系统的振动特性变得复杂;虽然载荷系数较小时仍存在周期运动,但系统运行过程中会发生脱啮,这也是需要避免的。
4 结论
(1)根据面齿轮啮合原理和受力分析,建立了考虑重合度、载荷分配率、综合传动误差、时变啮合刚度等时变参数的面齿轮传动系统6自由度弯扭摆非线性动力学模型。该模型可用于研究动态啮合力、啮合状态及其非线性动力学,有助于面齿轮传动系统齿廓变形和齿廓修形的研究。
(2)由于单对齿和双对齿的交替啮合,动态啮合力发生波动,动态啮合力的波动会导致啮合状态发生变化。当啮合状态变化时,动态啮合力发生突变。这是面齿轮传动系统中出现振动与噪声的根本原因。
(3)当载荷较大时,面齿轮传动系统的非线性动力学特性和振动特性稳定而简单;载荷较小时,会出现复杂的多状态啮合特性。
