基于LMD能量熵的齿轮箱故障诊断研究

2022-10-21朱玉斌郎超男

机械传动 2022年10期

徐乐李伟张博朱玉斌郎超男

（1 江苏师范大学工程实训中心，江苏徐州 221116）

（2 中国矿业大学机电工程学院，江苏徐州 221116）

0 引言

齿轮箱内部结构衔接紧密，具有体积小、质量轻、承载力强、传动比大等优点，被广泛应用在各类旋转机械装置中。齿轮箱长时间处于高强度连续运行状态，且运行环境较为恶劣，所以，发生故障的概率较高。而其一旦产生故障，将会导致机械装置无法工作，甚至可能引发事故，造成伤亡。因此，对齿轮箱运行状态进行监测，并对其故障进行诊断，具有重要意义。齿轮箱在发生故障后，其运行引起的振动信号是非线性、非平稳的，需要采用合适的方法对故障特征进行提取和分类，常用的方法有时域分析[1]、小波变换[2-3]、经验模态分解[4-5]等。在这些方法中，时域分析缺少频域成分，无法用于非线性振动信号分析；小波变换由于小波基选择困难，很难提取出较为理想的故障特征；经验模态分解在信号处理过程中迭代次数过多，端点效应明显，尤其是对非线性齿轮箱故障振动信号分析的自适应效果尚有差距[6]。

局部均值分解（Local mean decomposition，LMD）是Smith 首次提出的信号分析方法[7]，它可以将复杂的多分量信号自适应分解成若干个乘积函数（Product function，PF）的和，该方法对非线性、非平稳信号分析具有较强的适应性。相对于经验模态分解（EMD）方法，LMD 方法可有效抑制端点效应，解决了欠包络、过包络等问题；相对于集合经验模态分解（EEMD）方法，LMD 方法在信号分析过程中迭代次数较少，避免了分解过程中多个虚假分量的生成。程军圣等[8]利用LMD方法对齿轮故障振动信号进行分析，并将其与经验模态分解方法进行对比研究，证明了LMD方法的适应性和优势。李慧梅等[9]证明了LMD方法对齿轮故障特征的提取效果优于小波变换和Hilbert-Huang变换[10]。但是，由于LMD方法分解过程中局部均值函数和包络估计函数的求取与实际存在微弱误差，也会引发模态混淆问题。

齿轮箱出现故障后，其运行引起的振动信号会产生变化，主要表征是振动信号的能量会随着频率分布发生变化。为了依据各频域范围内能量分布变化提取出齿轮箱故障特征，周小龙等[11-13]利用LMD方法对齿轮箱振动信号进行分析，同时，为避免LMD 分解后的模态混淆问题影响，将熵理论引入，提出了能量熵概念。熵是用于描述系统中数据分布不确定性的量，能够衡量出分布紊乱程度，可有效表征出系统内部量的分布状况。本文中在研究LMD算法原理基础上，提出了基于LMD 能量熵的齿轮箱故障诊断方法，该方法利用LMD 方法对齿轮箱振动信号进行分析，得到有限个调频调幅信号；然后对分信号进行能量熵计算和处理，并进行了LMD 能量熵故障特征提取和齿轮箱故障诊断。

1 局部均值分解

LMD 是自适应的信号分解方法，能够将非线性、非平稳信号分解成若干个PF分量，各个PF分量由其相对应的包络信号与纯调频信号相乘得到[14-16]。LMD方法对于任一非线性、非平稳振动信号x（t）的分解步骤如下：

（1）找出信号x（t）的所有极值点ni（i=1，2，…），并计算出邻近极值点ni和ni+1之间的均值mi与它们的包络估计值ai，即

把得到的所有平均值mi和所有包络估计值ai依次分别连接起来，并用滑动平均法分别进行处理，得到局部均值函数m11（t）和包络估计函数a11（t）。

（2）将局部均值函数m11（t）从信号x（t）中分离，得到

（3）利用包络函数a11（t）对得到的h11（t）解调，得到调频信号s11（t），即

理想状态下，s11（t）是纯调频信号，即s11（t）对应的包络估计函数a12（t）=1。假如s11（t）对应的包络估计函数a12（t）≠1，则将s11（t）视作原始信号，重新上述迭代步骤，直至得出纯调频信号s1n（t），即s1n（t）符合-1≤s1n（t）≤1，s1n（t）对应的包络估计函数a1（n+1）（t）=1。

具体计算步骤为

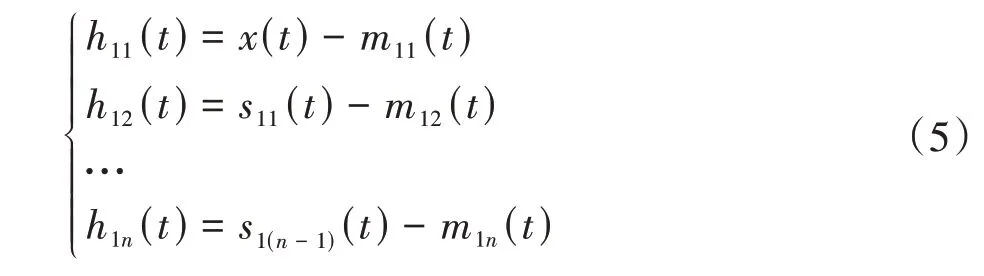
其中，

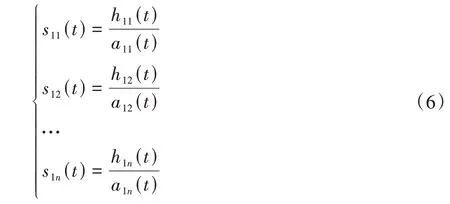
a1（n+1）（t）=1是得到的纯调频信号s1n（t）的理想状态。实际情况中，为了减少迭代次数、提高计算效率，在不改变分解结果前提下，增加微小偏差量Δ（Δ＞0），当1-Δ≤a1（n+1）（t）≤1+Δ，即认定s1n（t）是一个相对理想的纯调频信号。参考文献[17-18]和实验数据，Δ取值在[0.001，0.1]区间范围最适合。本文中在保证迭代结果正确及符合特征提取需要情况下，将Δ取值为0.05，即上述迭代终止条件为

（4）将迭代终止前得到的所有包络函数相乘得到包络信号a1（t），即

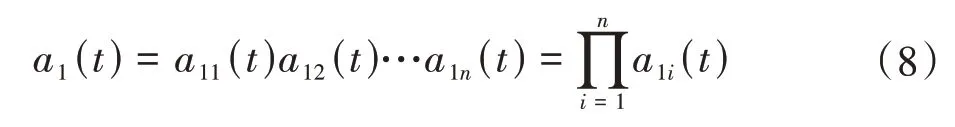
（5）将a1（t）与s1n（t）相乘，得到信号x（t）分解出来的首个PF分量，即

（6）在信号x（t）中将PF1（t）分离出去，剩余信号标记为u1（t）。把信号u1（t）当作新的信号，重复上述分解步骤，循环k次，直到uk（t）为单调函数为止。由于加入了微小偏差量Δ，实际循环k次后，uk（t）接近单调函数，即振幅趋于0。

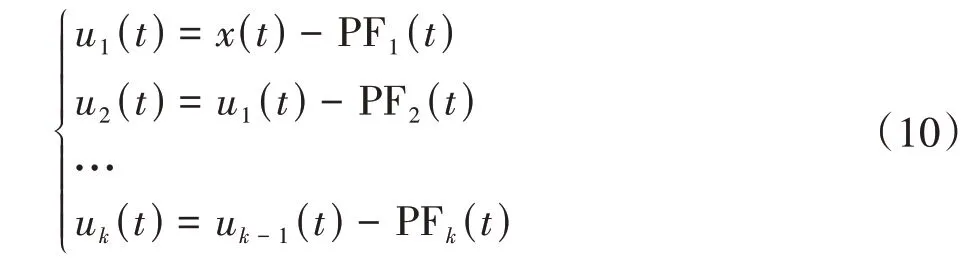
经过上述步骤，信号x（t）将被分解为k个PF 分量和1个残余量uk（t），即

LMD分解过程如图1所示。

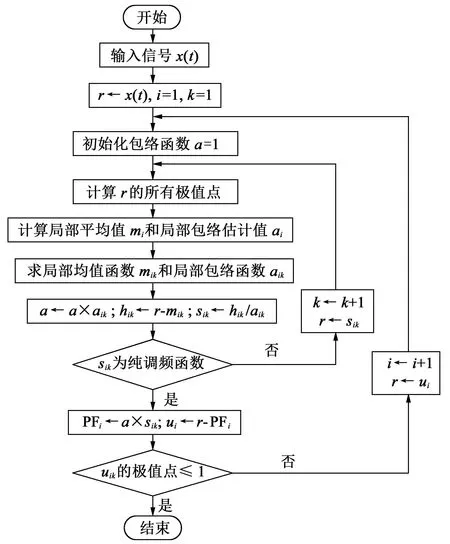
图1 LMD算法流程图Fig.1 LMD algorithm flow chart

2 LMD 能量熵

齿轮箱在正常状态和故障状态运行时，其引起的振动信号所包含的频率成分不同；而且，在不同故障下，其频率成分对应的能量分布也会发生改变。为了分析齿轮箱振动信号能量特征分布随信号频率成分的变化情况，定量地呈现出其分布紊乱程度，本文中将描述系统中数据分布不确定性的熵理论引入局部均值分解，提出了LMD 能量熵方法。该方法的原理及计算方式具体叙述如下。

非线性、非平稳振动信号x（t）被LMD 方法处理后，由k个PF 分量和残余量uk（t）组成，依次算出k个PF 分量所具有的能量，对应的能量值分别记为E1，E2，…，Ek。因残余量uk（t）为单调函数，其振动信号的能量几乎为0，因此，在不考虑残余量具有的微弱能量状态下，信号x（t）原本具有的能量与k个PF 分量具有的能量和相同。由于分解后的PF 分量分别为不同频域范围的信号成分，因此，E={E1，E2，…，Ek}就形成了振动信号能量特征在频率域内的自适应分布。因而，将LMD 能量熵计算方法定义为

式中，

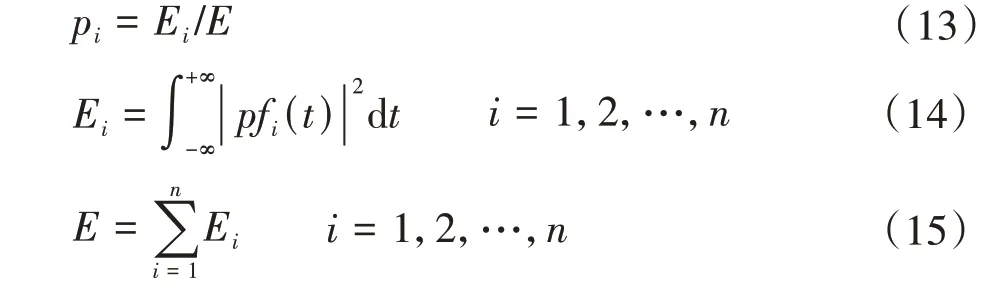
式中，Ei表示第i个PF分量的能量值。

3 基于LMD 能量熵的齿轮箱故障诊断方法

基于LMD 能量熵分析，结合实验数据对齿轮箱振动信号进行了特征提取和故障诊断，具体步骤如图2所示。

图2 齿轮箱故障诊断步骤Fig.2 Gearbox fault diagnosis steps

首先，在齿轮箱故障模拟实验台上设置齿轮箱振动信号拟选择的采样点数及频率，为实现对复合故障的诊断，分别采集了断齿、磨损、断齿+磨损3种故障及正常齿轮运行引起的振动信号；其次，利用LMD 方法分别对采集的每组振动信号进行处理，每组信号经LMD 分解后得到k个PF 分量和残余量uk（t）；然后，将k个PF 分量作为计算元素，计算出每个分量的能量值；最后，计算出每组信号的LMD能量熵，从而提取出齿轮箱在不同状态下的故障特征，并通过能量熵值分布特性实现齿轮箱故障诊断。

4 实验分析

为了验证LMD能量熵方法对齿轮箱故障诊断的效果，选择在QPZZ-Ⅱ旋转机械故障模拟试验台进行了不同故障齿轮振动数据采集。试验台装置如图3所示。

图3 旋转机械故障模拟试验台Fig.3 Rotating machinery fault simulation test bench

试验台由变速驱动电机、联轴器、齿轮箱、磁粉扭力器等部件组成，为了在离故障齿轮最近的位置同步测得有效可用振动数据，齿轮箱盖的水平、垂直方向分别安装1 个加速度传感器，并利用ADA16-8/2（LPCI）采集卡采集实验振动数据。齿轮故障模拟实验装置简图如图4所示。实验中，除采集正常齿轮箱振动数据外，还通过更换不同故障的大、小齿轮采集了故障数据，包括小齿轮断齿、大齿轮磨损、小齿轮断齿+大齿轮磨损3 种故障；实验齿轮如图5所示。其中，断齿通过铣削加工去除掉1个齿来模拟断齿状态；齿轮磨损通过磨齿机将齿轮齿面单边打磨掉0.2 mm 厚度来模拟磨损状态；实验齿轮的基本参数如表1所示。

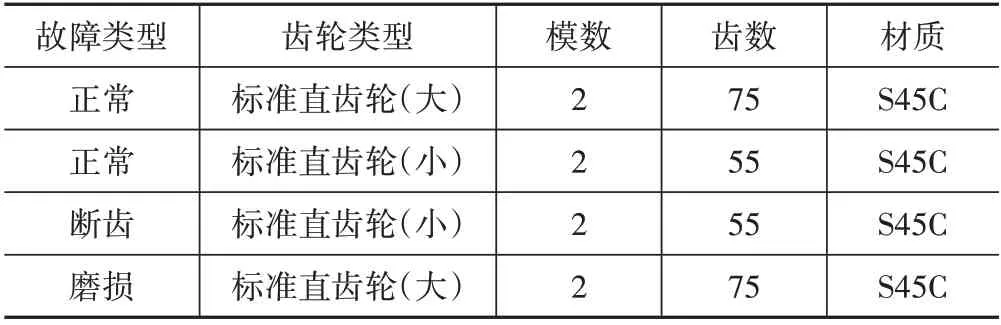
表1 实验齿轮基本尺寸参数Tab.1 Basic dimension parameters of experimental gears

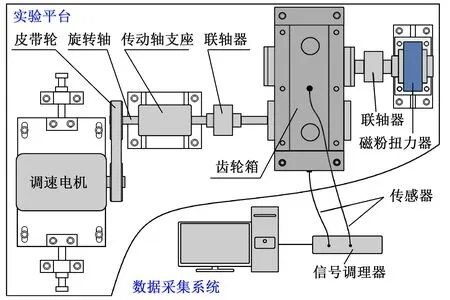
图4 齿轮故障模拟实验装置简图Fig.4 Schematic diagram of gear fault simulation experiment device

图5 实验齿轮Fig.5 Experimental gears

齿轮箱振动信号采集实验中，电机平均转速为1 470 r/min，设置采样频率为5 120 Hz、采集点数为2 000。在空载相同条件下分别对4 种齿轮工作状态振动信号进行采样，为了实现小样本分析需求（样本数不得超过30），每种状态分别采集10组振动数据。

根据第1 节中提出的LMD 分解方法，对采集的每组齿轮箱振动信号进行LMD 分解，得到若干PF分量和1 个残余量。图6 所示为以一组断齿故障为例，利用Matlab 程序将原始信号调入，经LMD 分解后得到的5 个PF 分量和1 个残余分量。从分解结果能够看出，LMD 分解后的各个PF 分量将原始信号按照从高到低顺序分离出信号的分辨率，残余量u5（t）接近单调函数，能量接近于0。

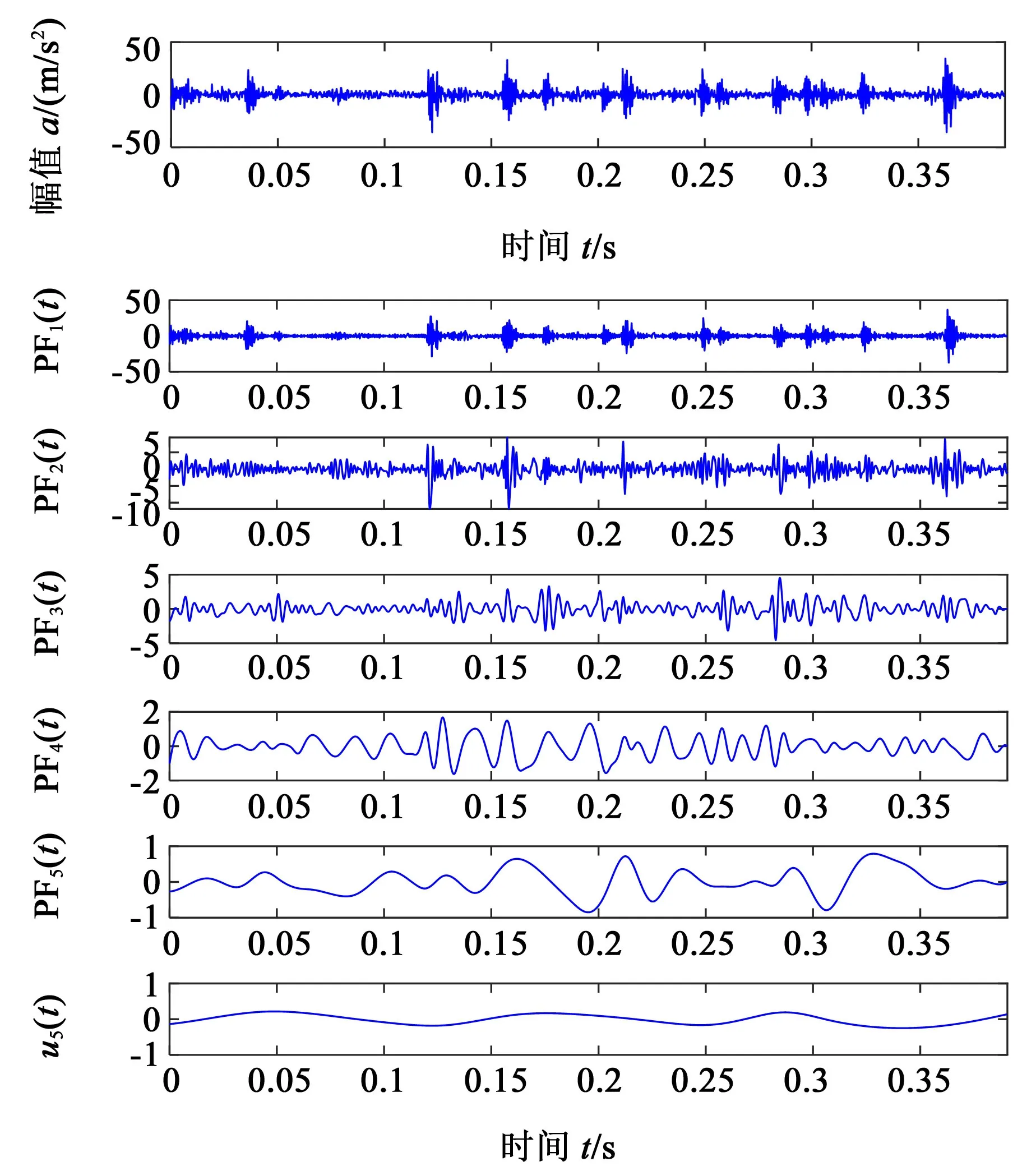
图6 断齿状态原始振动信号及LMD分解结果Fig.6 Original vibration signals in broken tooth state and its LMD decomposition results

依次对4 种状态下的齿轮箱振动信号进行LMD分解，并求取了各PF 分量能量及对应的能量熵。分别对4种状态的10组振动信号进行分析，图7所示为40 组振动信号经LMD 分解后的前5 个PF 分量对应的能量值分布。从图7中能够看出，虽然每种状态对应的PF 分量能量值保持在一定的区间范围，但都存在跳跃现象，即不同状态下的能量值出现区间交叉重合；导致这一现象的主要原因是当齿轮发生故障时，振动引起的能量存在交叉，如断齿与正常齿轮相比，齿轮转动1周仅相差1次振动突变，整体能量差距较少；如断齿或磨损与断齿+磨损故障相比，后者包含前者任一故障，因此，整体能量也介于两者之间。

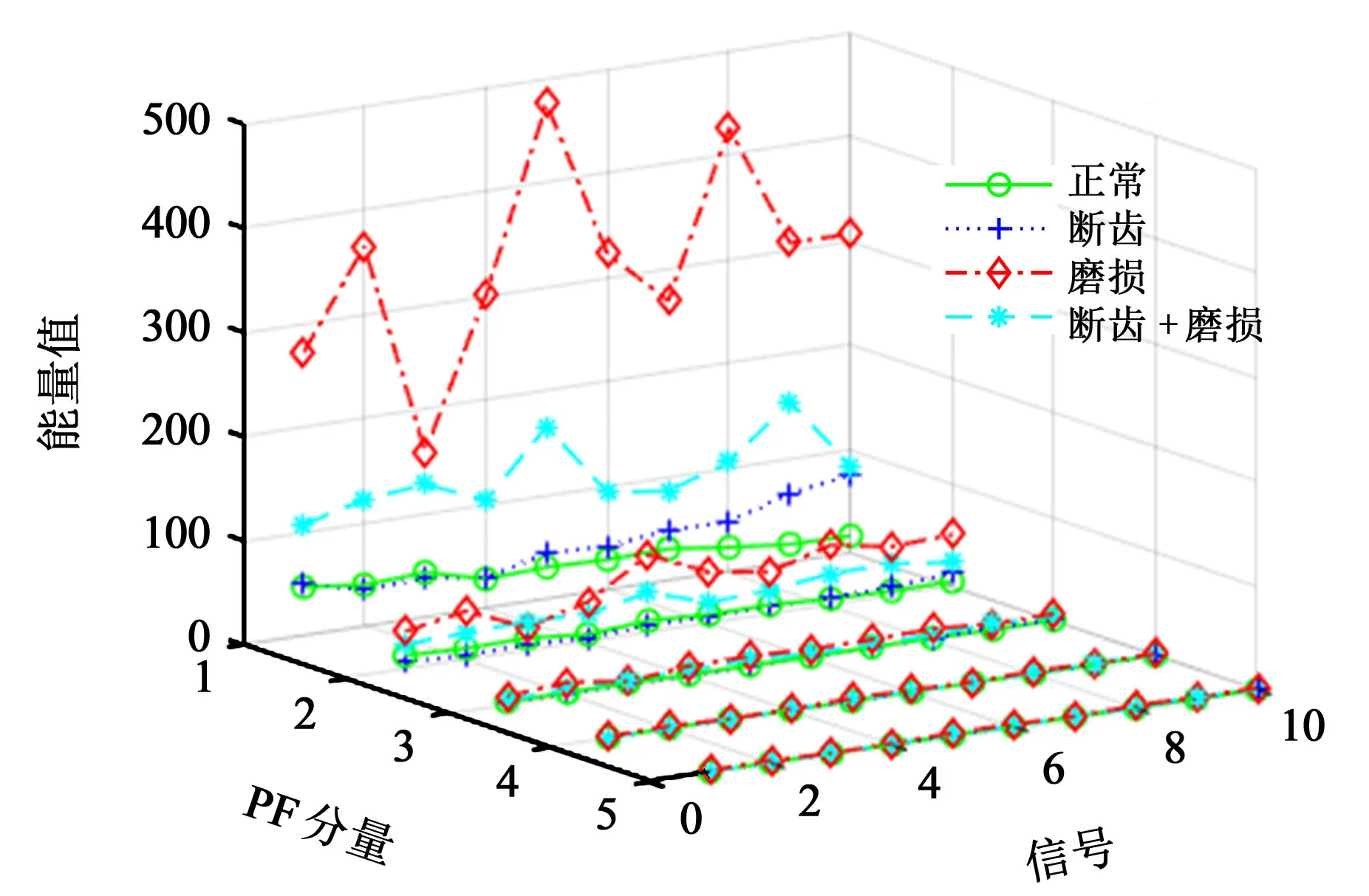
图7 训练样本PF能量值分布图Fig.7 PF energy value distribution of training samples

但是，从表2 和图8 所示40 组振动信号对应的LMD 能量熵值中能够看出，即使分解后的PF 分量能量值出现了交叉和跳跃，振动信号对应的LMD 能量熵仍具有明显的状态区分规律，证明LMD 能量熵特征值能够把不同状态下的齿轮箱故障有效区分出来。由图8中可知，LMD能量熵值处于0.7～0.8之间为磨损；处于0.8～0.9 之间为断齿；处于0.95～1.1 之间为断齿+磨损；处于1.1以上为正常状态。

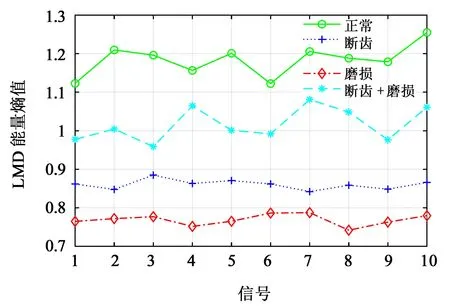
图8 训练样本LMD能量熵值分布图Fig.8 LMD energy entropy distribution of training samples

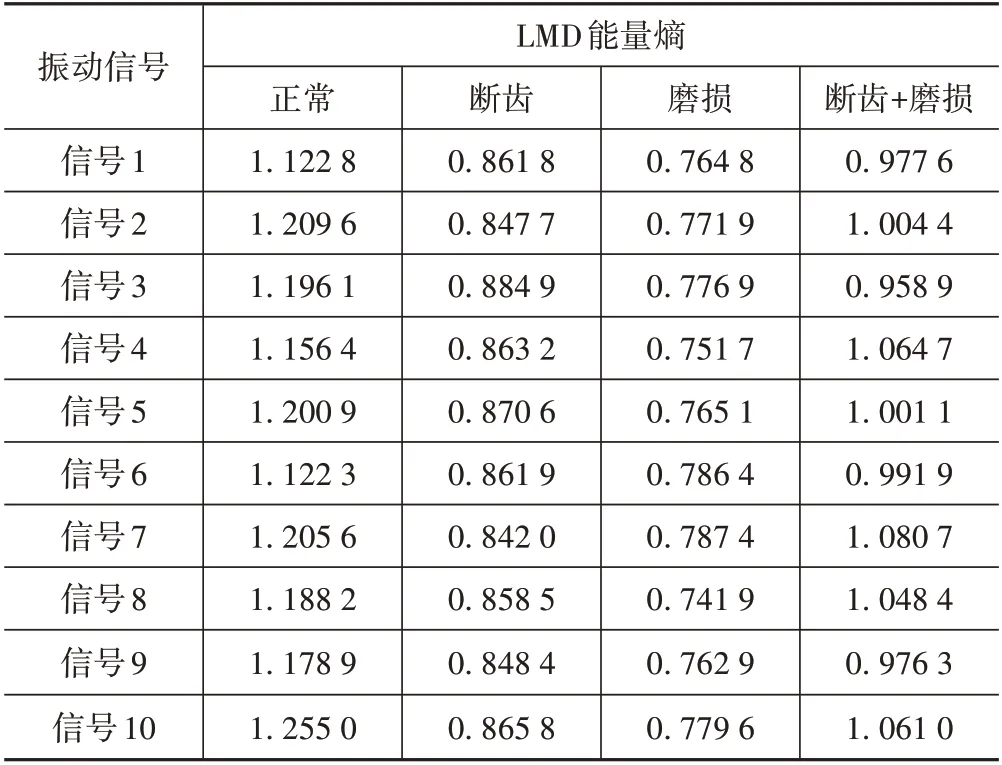
表2 训练样本LMD能量熵Tab.2 LMD energy entropy of training samples

从图8 中的LMD 能量熵分布情况中还能够看出，正常状态下的齿轮箱振动信号对应的LMD 能量熵值高于故障状态齿轮箱对应的值，这是由于齿轮箱未发生故障时，其运行状态相对较为平稳，对应的振动信号在各频域内分布也较为均衡，能量在各频域范围内不确定性程度相对较大，能量熵值也就较高。当齿轮箱出现故障时，振动信号会有一部分集中在其故障频率区域内，因此，振动信号在频域区间内分布相对聚集，不确定性相对较小，故对应的能量熵低于未发生故障齿轮。而且，当齿轮箱出现磨损故障时，其每一个齿面都是均匀磨损，齿轮的啮合频率及其谐波的幅值增大，故障频率集中在啮合频率区域，振动频率相对一致，不确定性最小，因此，能量熵最小；当齿轮箱出现断齿故障，齿轮啮合频率及其谐波为载波频率，故障齿轮所在轴的转频及其倍频为调制频率，调制边频带宽而高，振动频率相对复杂，不确定性相对较大，能量熵也就相对大；当齿轮箱同时出现小齿轮断齿和大齿轮磨损两种故障时，振动信号会在两种故障频域上分散，因此，断齿+磨损状态下振动信号对应的LMD 能量熵要比两种单独故障状态的高。