基于CNN-LSTM的轴承剩余使用寿命预测

2022-10-21蔡薇薇徐彦伟颉潭成

机械传动 2022年10期

蔡薇薇徐彦伟，2 颉潭成，2

（1 河南科技大学机电工程学院，河南洛阳 471003）

（2 智能数控装备河南省工程实验室，河南洛阳 471003）

0 引言

技术进步促进交通工具革新，现代铁路，尤其是高速铁路，扮演着举足轻重的角色[1]。对铁路轴承疲劳寿命进行准确预测，一直是铁路学者们关心而又难以解决的课题[2]。当前，对机械设备中的关键部件采用剩余使用寿命（Remaining useful life，RUL）预测技术，来决定维修管理时机的方法得到越来越广泛的重视[3]。RUL 综合反映了机械设备关键部件的受损程度，通过对RUL 预测技术的研究，能提前发现机械设备中关键部件的异常，对其未来的性能退化趋势进行研究，及时进行有效维护[4]。如果在轴承失效前可准确地预测出其剩余使用寿命，便可及时采取预防措施，从而避免造成重大的经济损失。

滚动轴承剩余寿命预测方法大致可分为基于模型驱动和基于数据驱动两大类[5]。丁锋等[6]采用基于设备振动信号的均方根、峭度等统计特征，利用比例故障模型实现了对铁路机车轮滚动轴承的可靠性评估。王奉涛等[7]将通过核主元分析降维后的核主元作为威布尔比例故障模型的协变量估计模型参数，对滚动轴承进行剩余寿命预测，取得了很高的准确度。王豪等[8]将多个特征组合为一个特征树，将优化特征作为模型，对轴承剩余寿命进行了预测。这些基于模型驱动的方法能够对滚动轴承剩余寿命进行比较准确的预测，但对于复杂的机械系统存在难建模、预测精度低等缺点。计算机技术的发展对研究数据驱动的机械设备剩余寿命预测方法有极大的推动。高斯博[9]利用线性Wiener 过程，陈法法等[10]使用小波支持向量机，李洪儒等[11]使用极限学习机进行了剩余寿命预测。但这些方法需要先进行人工构造特征，并且在模型复杂度和学习能力上与深度学习方法有一定差距。随着现代计算能力的快速提升和计算效率的提高，深度学习方法因其在复杂系统中强大的学习能力，已成为预测领域的新兴研究课题之一[12]。在大多数情况下，深度学习方法可利用振动信号来监测滚动轴承的健康状况，因为信号中包含了故障发生的重要信息[13]。申彦斌等[14]提出了一种基于双向长短时记忆网络的循环神经网络结构，利用其对处理时间序列数据的能力，对轴承在实际工作过程中的退化规律进行学习，实现了对轴承的剩余使用寿命预测。董绍江等[15]针对滚动轴承退化性能难以评估、寿命状态难以识别的难题，基于卷积自编码器与多维尺度分析算法构建轴承性能衰退指标，再根据构建指标和改进卷积神经网络建立轴承寿命状态识别模型，实现了轴承寿命状态的识别。康守强等[16]针对稀疏自动编码器采用Sigmoid 激活函数容易造成梯度消失的问题，提出了一种新的Tan函数替代原有的Sigmoid 激活函数，并采用Dropout 机制对网络进行稀疏性约束，将提取出的深层特征作为滚动轴承的性能退化特征，实现了对滚动轴承的RUL 预测。这些研究都取得了很好的结果，但都是针对单工况数据进行的研究。

针对以上问题以及设备到达服役时间而依然健康所造成的浪费问题，本文中对完成服役时长仍健康的高铁牵引电机轴承进行试验，并使用深度学习方法建立剩余寿命预测模型，直接从原数据挖掘出有用的信息，对轴承的剩余使用寿命进行了预测。

1 高铁牵引电机轴承试验

1.1 高铁牵引电机轴承试验台

高铁牵引电机轴承剩余寿命试验台与信息采集系统由试验主体、高铁牵引电机轴承NU210、液压加载系统、传感器信息采集模块、通风设置及计算机等组成，整体结构如图1所示。试验台主轴转速范围为0～6 000 r/min，靠近试验轴承箱处的风速为8～10 m/s。

图1 高铁牵引电机轴承试验台Fig.1 High speed railway traction motor bearing test bench

1.2 采集系统

如图2 所示，采集系统由2 个振动传感器（型号为LC0151T，灵敏度为150 mv/g，量程为33 g，分辨率为40 kHz，谐振频率为0.000 2 kHz，频率范围为0.7～13 000 Hz）、1 个信号放大器、1 个信号调理器（型号为LC0201-5）、PCI采集卡（型号为PCI8510，8通道同步采样，采样频率为500 kHz）和计算机组成。由振动传感器采集的电流型信号经信号调理器处理为电压型信号，再通过PCI采集卡存至计算机，最终由计算机实现对信号的分析及处理。

图2 采集系统原理简图Fig.2 Schematic diagram of acquisition system

1.3 试验参数及试验方案

本次试验是将已运行1.45×106km 里程数，完成其服役工作后仍健康的高铁牵引电机轴承NU210再运行2.7×105km 的里程。根据实际工况，试验过程中轴承所受径向载荷为5 kN，由于高铁实际运行中Vmax≥200 km/h，参考TB/T 3017.2—2016[17]要求，本文中采用4 h 循环试验，即试验主轴先正向转动105 min，停止15 min，再反向转动105 min，停止15 min，在停止期间不进行通风。

该高铁线路单程里程数为968 km，1个往返循环的里程数为1 936 km，完成试验需要进行140个循环。为更好地模拟高铁牵引电机实际工作状态，每天进行4 个循环（即7∶00～11∶00，11∶00～15∶00，15∶00～19∶00，19∶00～23∶00）。试验安排如表1所示。

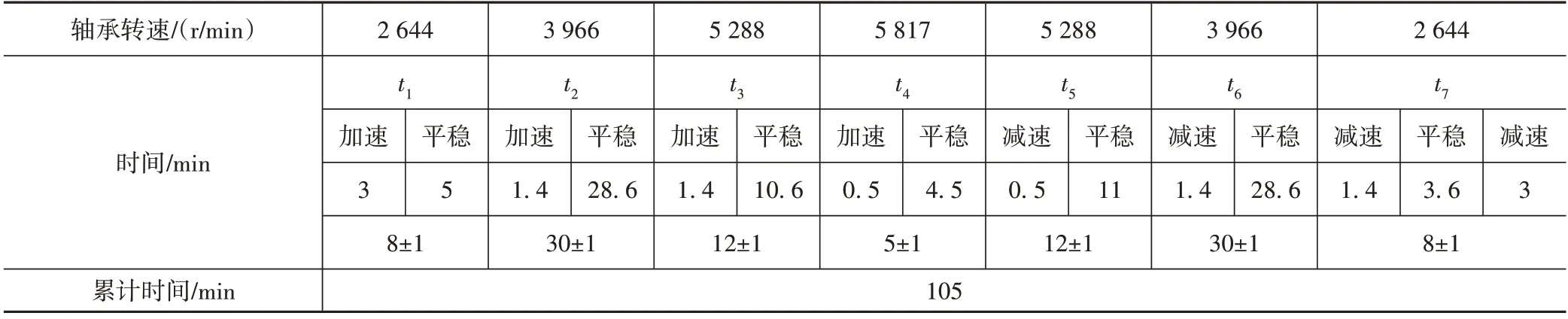
表1 试验安排表Tab.1 Test schedule

2 CNN-LSTM 模型的建立

2.1 一维卷积神经网络

对于传感器数据在时间序列的分析，一维神经网络有着较强的特征提取能力，可以被用于固定长度信号的分析[18]。其卷积层和池化层的数学模型分别为式中，W为池化区域的宽度；(t)为第l层中第i个特征矢量中的第t个神经元的值；t∈[（j-1）W+1，jW]；P(j)为第l+1层中神经元对应的值。

2.2 长短时记忆网络

长短时记忆网络（LSTM）是循环神经网络（RNN）的改进，具有长时间和短时间的序列记忆，可以学习到序列之间潜在的时间关系[19-20]。LSTM 原理的数学模型为：

（1）计算输入门需要保存的信息

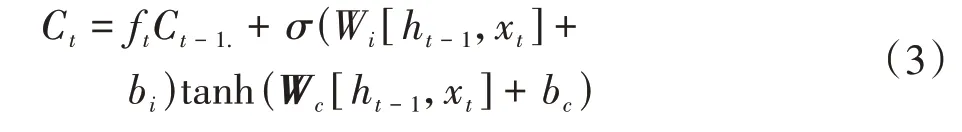
式中，Ct为LSTM 输入门中的细胞状态信息；Ct-1为上一个细胞状态信息；Wc为权重矩阵；bc为偏置参数；tanh 为激活函数。

（2）计算遗忘门需要删除的信息

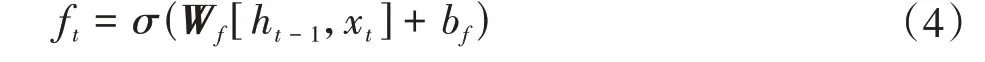
式中，xt为输入的特征矢量；σ为sigmoid 激活函数；Wf为训练的权重矩阵；ht-1为上一时刻的隐藏层信息；bf为偏置参数；ft为保留信息的权重。

（3）计算输出门需要输出的信息

式中，ht为输出门的输出信息；Wo为训练的权重矩阵；bo为偏置参数。

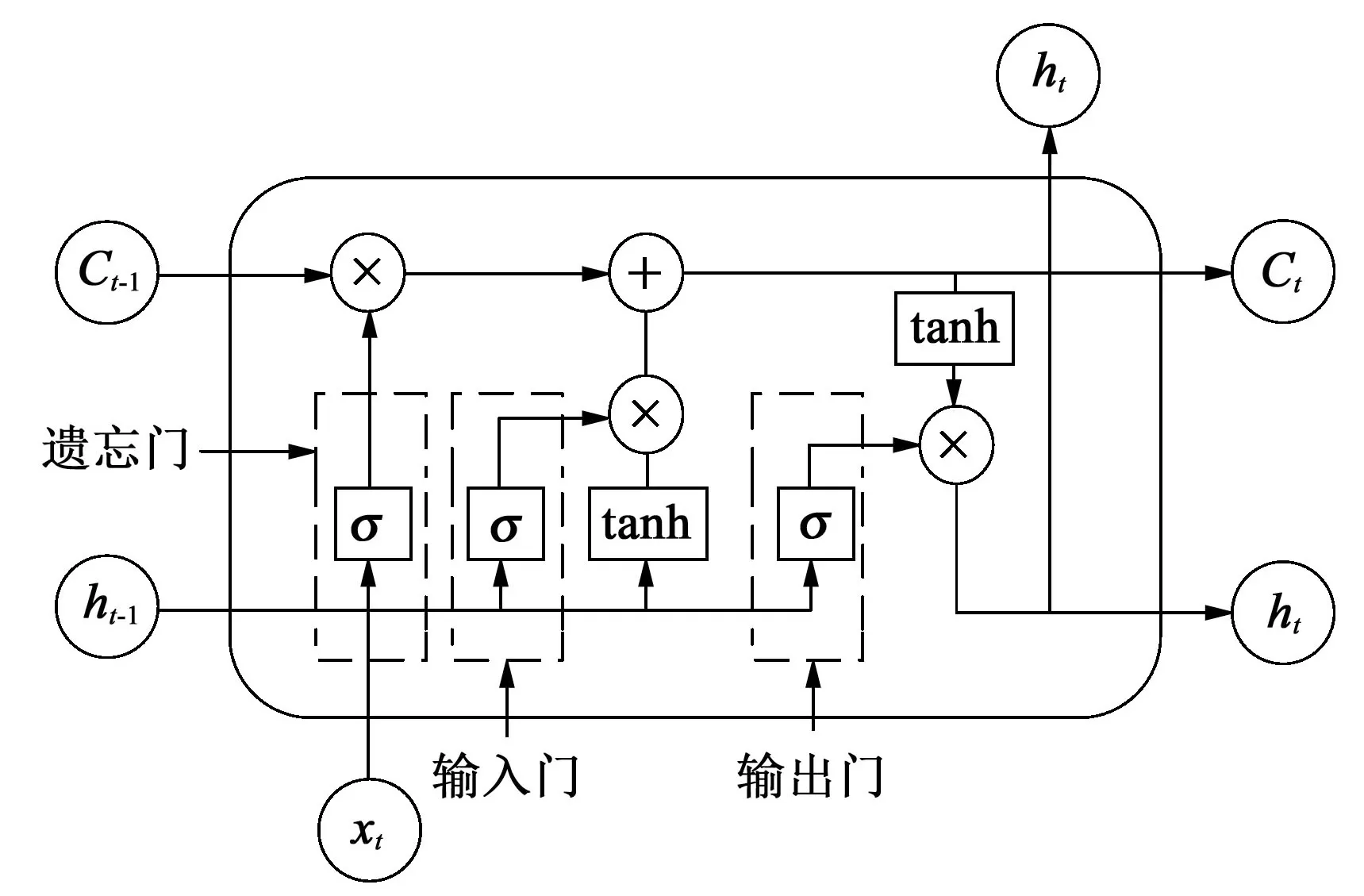
图3 LSTM网络结构图Fig.3 LSTM network structure diagram

2.3 基于CNN-LSTM 的轴承剩余使用寿命预测方法

图4所示为剩余使用寿命预测流程图。其流程各模块的功能为：

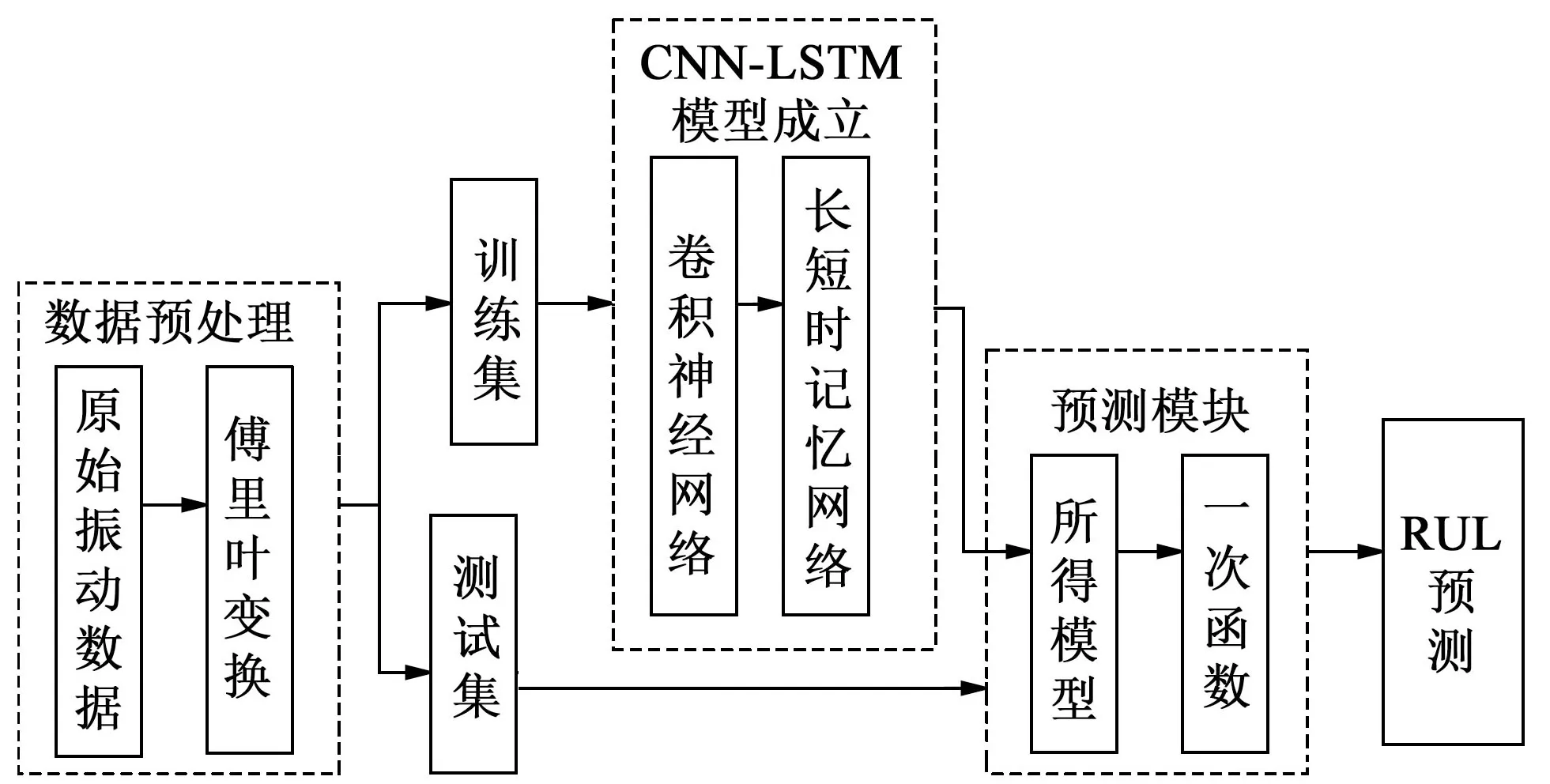
图4 剩余使用寿命预测流程图Fig.4 Flow chart of remaining service life prediction

数据预处理：把原始振动数据经过FFT 变换，转化为频域信号；把数据集划分为测试集和训练集。

CNN-LSTM 模型：输入为频域信号，CNN 学习振动信号不同频带的特征，再通过LSTM 学习序列数据潜在的时间关系，对其深层特征进行有效挖掘，进而输出当前剩余使用寿命的状态值。

预测模块：测试集输入建立的CNN-LSTM 模型中，输出为当前状态值C，再根据一次函数，输出剩余使用时间。剩余使用时间Fc的表达式为

式中，Ctc为总特征值；Ccc为当前特征值。

3 滚动轴承RUL预测

本文中以50 kHz的采样频率，每5 min采集1次，每次采集时长为1 s 的方式对高铁牵引电机轴承的振动信号进行采集。每次采集50 000个数据点，每个循环有42个采集点，试验共有5 880个采集样本。

根据香农采样定理，选择每2 275个数据为1组小样本。本文中把每个采样点分为前后两部分，即45 450 个数据点和4 550个数据点。图5所示为数据分段。将前半段的45 450个数据点采用重叠采样的方法分成50组小样本数据，作为训练集，各组小样本数据含有2 275个数据点；后半段数据不进行重叠采样，直接截断成2个数据长度均为2 275的小样本作为测试集。

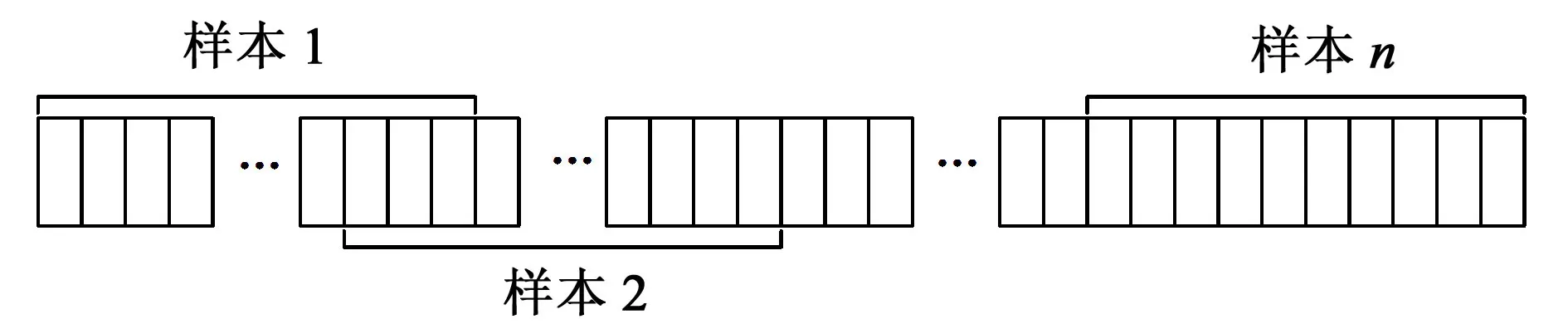
图5 数据分段Fig.5 Data segmentation

本文中的数据分析均以试验轴承2 为例。图6、图7所示分别为试验轴承2在2 644 r/min和5 817 r/min时某样本的时域及频域信号图。

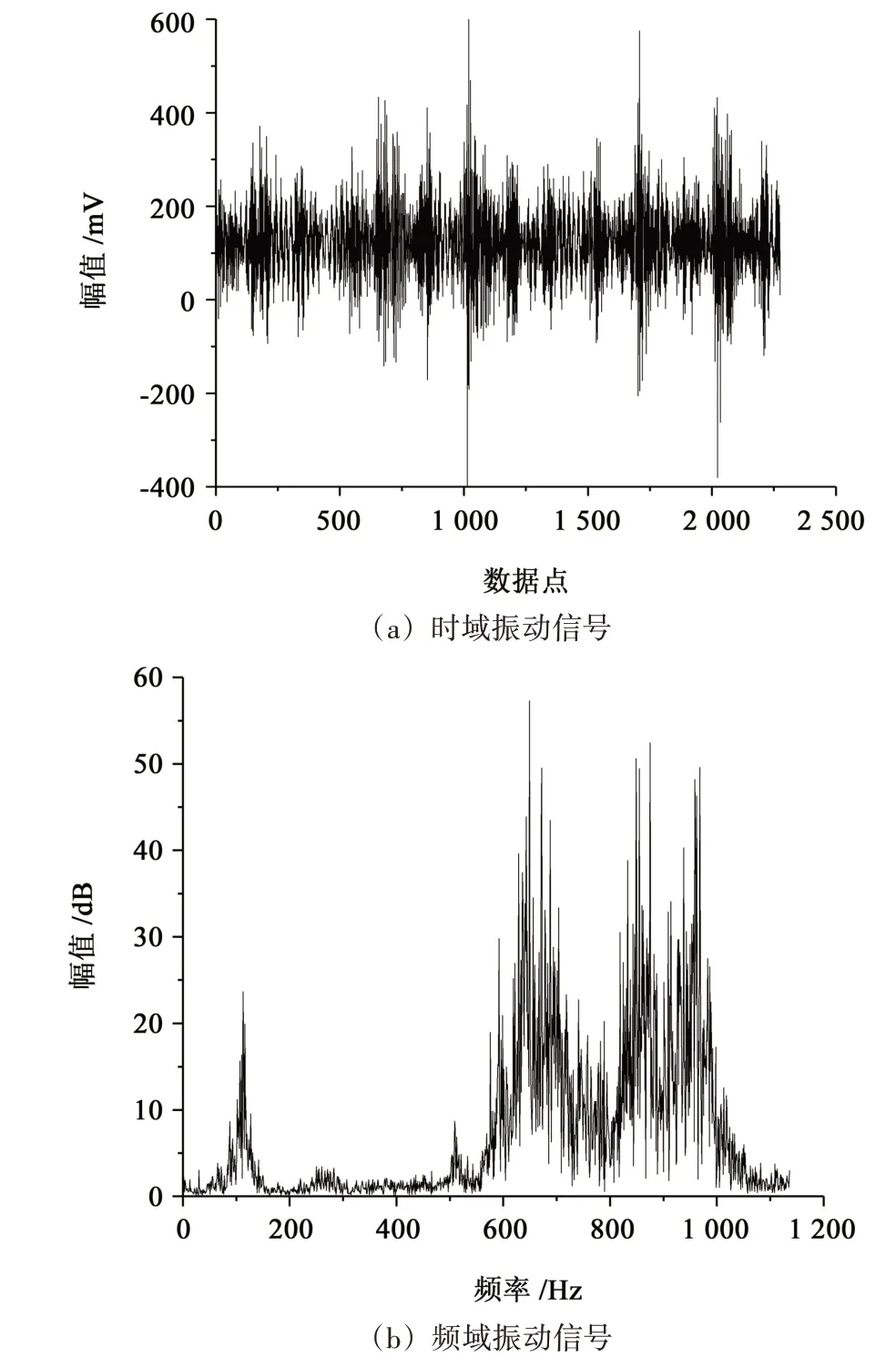
图6 2 644 r/min时某样本时域及频域信号波形图Fig.6 Time domain and frequency domain signal waveform of a sample at 2 644 r/min

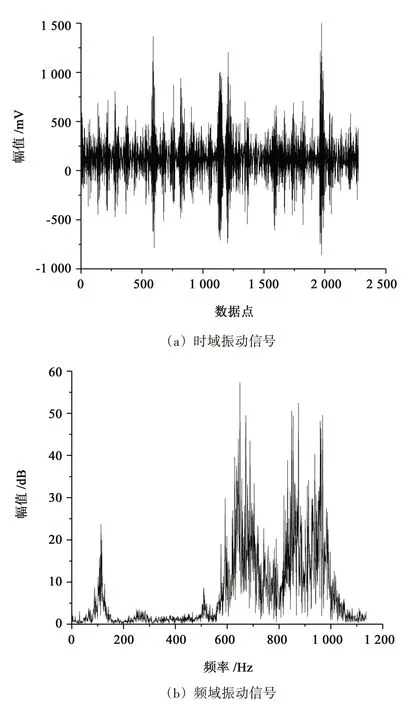
图7 5 817 r/min时某样本时域及频域信号波形图Fig.7 Time domain and frequency domain signal waveform of a sample at 5 817 r/min

根据单次循环转速的变化，把试验数据分为6部分。表2所示为各部分原数据按以上分段处理后得到的数据集。这6 部分都包含了140 种状态值。其中，编号0、编号2、编号3、编号5 中的各状态中包含7种特征点，编号1、编号4 的各状态中包含6 种特征点。

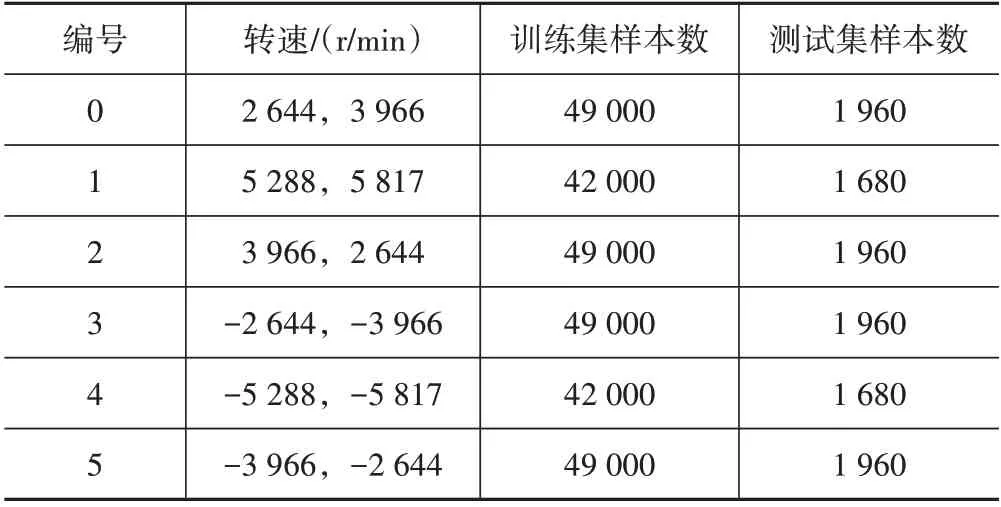
表2 试验数据集描述Tab.2 Test data set description

经多次调试，最终确定CNN-LSTM 模型的组成部分为：2个卷积层、2个池化层、1个LSTM 层。在卷积层前添加了1 个BN 层。其中，卷积层激活函数选用Relu，LSTM 层激活函数选用Tanh。之后，添加1 个输出维度为256 的全连接层；接着，添加1 个比率设置为0.2 的Dropout 层；最后，再添加1 个输出维度为140 的softmax 分类器。该模型使用交叉熵损失函数作为其损失函数，选用Adam 优化器进行梯度优化，batch_size 为128，epoches 为35。得到6 部分数据集的预测准确率依次为97.72%、94.98%、96.96%、91.31%、94.06%和94.75%。

将各测试集输入到训练好的网络模型中，得到预测的当前状态值及当下特征点。以第二部分数据为例，其预测状态值和实际状态值如图8所示。

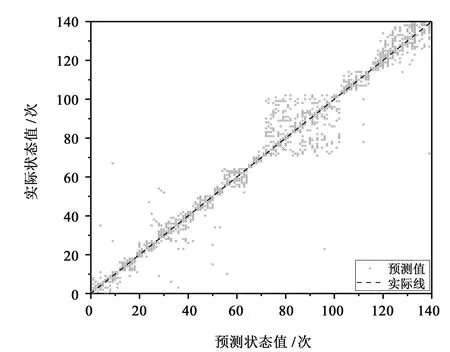
图8 状态值预测图Fig.8 State value prediction diagram

对预测状态值进行了6 种方法的拟合，即：线性拟合、2 阶、5 阶、9 阶多项式拟合、以Boltzmann为模型和以Allometric1 为模型的非线性曲线拟合。表3 所示为拟合曲线参数表。线性拟合和以Allometric1 为模型的非线性曲线拟合的相关系数R2均为0.979 16；当阶数为9 时，多项式拟合的相关系数最大，为0.981 10，比线性拟合的相关系数高0.001 94。

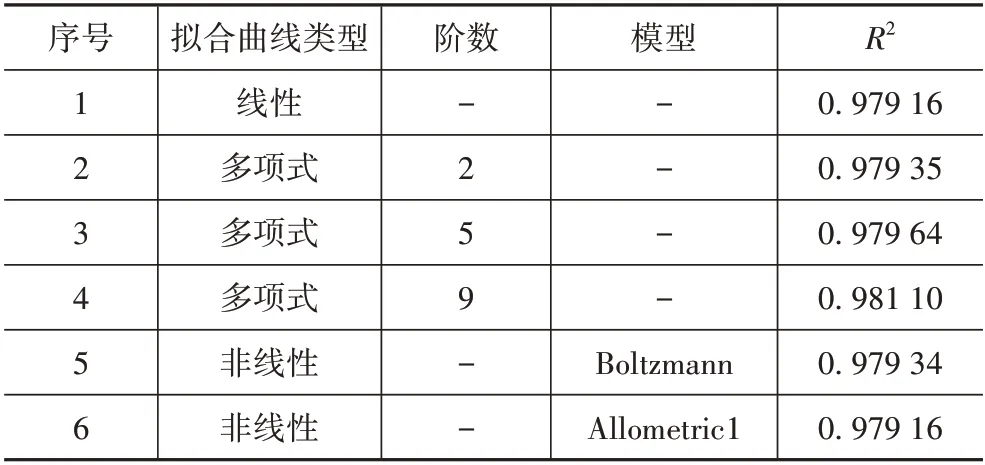
表3 拟合曲线参数表Tab.3 Fitting curve parameter table

综合看来，这6 种拟合方法的相关系数差别不大。与其他5种相比较，线性拟合函数简单，表示能力强。本文中选择线性拟合作为拟合方法。

第二部分的线性拟合图如图9所示。

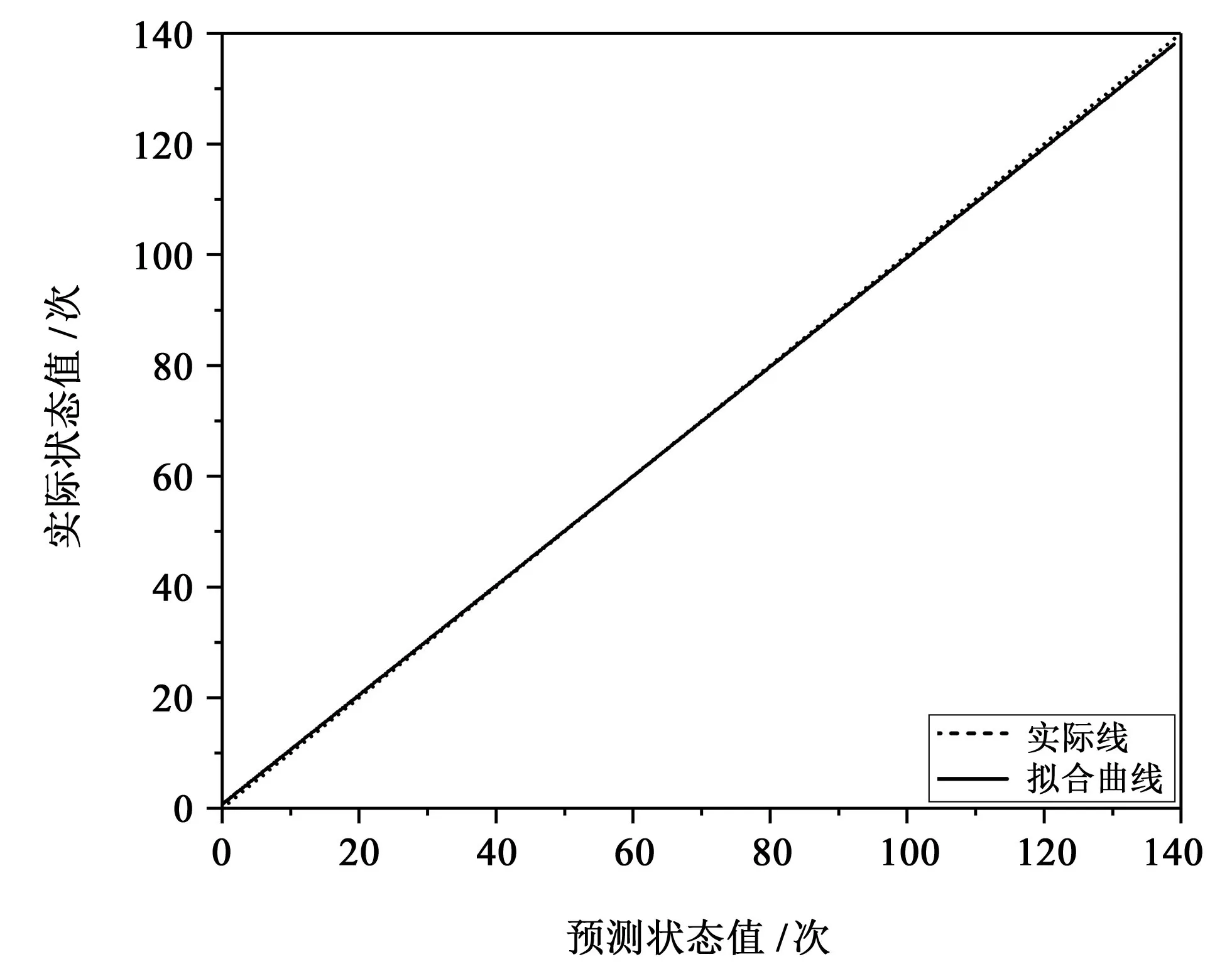
图9 线性拟合图Fig.9 Linear fitting diagram

表4所示为各部分预测结果的线性拟合参数。其中，a为斜率；b为截距；R2为相关系数。各参数取小数点后3位。

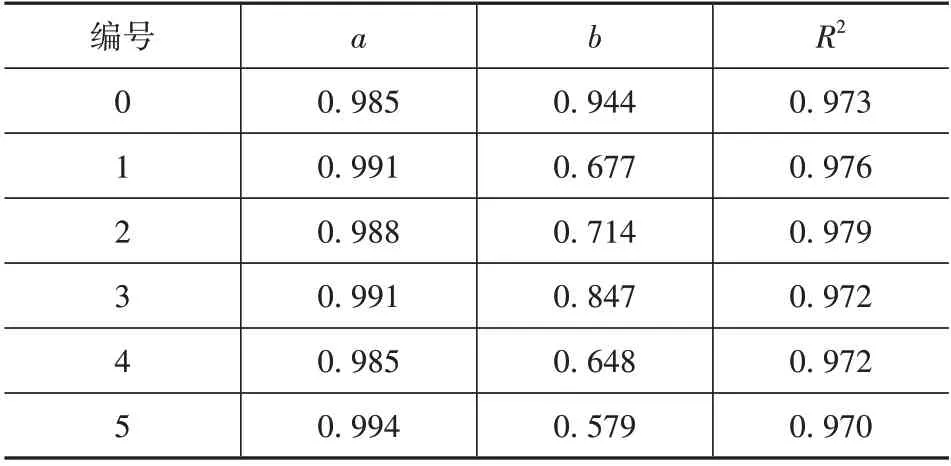
表4 线性拟合参数表Tab.4 Linear fitting parameter table

本文中试验轴承2 的采样数据共5 880 个，每个特征点表示的寿命是5 min。通过式（6）可计算出当前特征点的剩余使用寿命；之后，利用式（7）预测寿命百分比误差Ec，评估模型性能的优劣，有

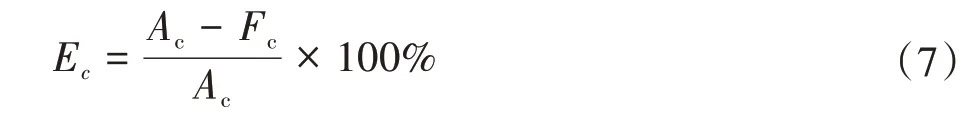
式中，Ac、Fc分别为当前特征点的实际剩余使用寿命和预测剩余寿命。

Ec＞0 表明RUL 预测结果偏小；Ec＜0 表明RUL 预测结果偏大；Ec=0表明RUL预测误差为0。将采集的5 880 个数据点代表的寿命作为实际寿命，得到6 部分数据集的预测寿命百分比平均误差分别为3.48%、9.59%、7.20%、8.09%、16.77%、7.42%。

表5 所示为部分RUL 预测结果。在各6 部分中随机选择5 个预测点，其中，Fc1是用预测的当前状态值得到的剩余使用寿命；Fc2是预测的状态值经过线性拟合后得到的剩余使用寿命。0-1 测试点处于第22 个循环的第1 个特征点，其当前特征值为22×42+1=925，实际RUL 为（5 880-925）×5=24 775 min，其特征点不发生改变，预测状态值为23，得到Fc1为[5 880-（23×42+1）]×5=24 565 min，其预测误差为（24 775-24 565）/24 775=0.85%，预测状态值经过线性拟合后为23，得到的Fc2为24 565 min，Ec2为0.85%。由表5中可以看出，直接使用预测状态值得到的预测结果较好。